Когда требуется разрешение лучше 16 двоичных разрядов при высокой частоте выборок, рассматривавшиеся до сих пор методы преобразования становятся недостаточно эффективными, особенно при малых уровнях сигналов. Требование точно откалиброванного многоразрядного ЦАП в качестве элемента схемы преобразования становится чрезмерно жестким. Даже малые отклонения уровней на выходе ЦАП от их номинальных значений, обусловленные разбросом параметров и различное время срабатывания ключей могут привести к провалам в проходной характеристике и даже к пропуску отдельных двоичных комбинаций на выходе.
Скоростные цифровые схемы позволяют создавать преобразователи, действующие по принципу избыточной дискретизации и работающие с частотой выборок, значительно превосходящей теоретический минимум, определяемый шириной занимаемой сигналом полосы. Выгода от применения избыточной дискретизации заключается в том, что спектр шума квантования можно распределить по более широкому интервалу частот. Это дает возможность большую часть шума оставить вне зоны используемых частот при обратной фильтрации дискретизованного сигнала с сохранением компонентов только в полосе исходного сигнала.
Рассмотрим методику избыточной дискретизации с анализом в частотной области. Там, где преобразование постоянного напряжения имеет ошибку квантования до ½ младшего разряда (МЗР), дискретная система, работающая с переменным входным сигналом, обладает шумом квантования. Идеальный классический N-разрядный АЦП имеет среднеквадратичное значение шума квантования, равное h/
√12. Шум квантования равномерно распределен в пределах полосы Котельникова от 0 до fВ/2 (где h – значение младшего значащего бита и fв — частота дискретизации), как показано на рисуноке(а). Поэтому, его отношение сигнал/шум для полнодиапазонного синусоидального входного сигнала будет (6,02N+1,76)дБ. Если АЦП несовершенен и его реальный шум больше, чем его теоретический минимальный шум квантования, то эффективная разрешающая способность будет меньше, чем N-разрядов.
Если выбрать более высокую частоту дискретизации K fВ ( а),
Спектры шумов квантования в простом АЦП (а), АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (б) и Σ∆-АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (в)
то среднеквадратичное значение шума квантования остается h /√12, но шум теперь распределен по более широкой полосе от 0 до fВ /√12. Если затем использовать на выходе цифровой низкочастотный фильтр, то значительно уменьшится шум квантования, но сохранится полезный сигнал, улучшая таким способом эффективное число разрядов. Таким образом, выполняется аналого-цифровое преобразование с высоким разрешением при использовании аналого-цифрового преобразователя с низкой разрешающей способностью. Коэффициент K здесь упоминается, как коэффициент избыточной дискретизации. При этом необходимо отметить, что избыточная дискретизация дополнительно выгодна еще и тем, что она понижает требования к аналоговому ФНЧ.
Analog-to-Digital Converters (ADC) — Charge-Balancing and Delta-Sigma ADC
Так как ширина полосы пропускания уменьшена выходным цифровым фильтром, скорость выдачи выходных данных может быть ниже, чем первоначальная частота дискретизации (KfВ), и при этом все же удовлетворять теореме Котельникова. Это достигается посредством передачи на выход каждого М-го результата и отбрасывания остальных результатов. Такой процесс называют децимацией с коэффициентом М. Несмотря на происхождение термина (decem по-латыни — десять), М может принимать любое целое значение, при условии, что частота выходных данных больше, чем удвоенная ширина полосы сигнала. Прореживание не вызывает никакой потери информации рисунок (б).
Если использовать избыточную дискретизацию только для улучшения разрешающей способности, необходимо применять коэффициент избыточности 2 2N , чтобы получить N- разрядное увеличение разрешающей способности. Сигма-дельта (Σ∆) преобразователь не нуждается в таком высоком коэффициенте избыточной дискретизации. Он не только ограничивает полосу пропускания сигнала, но также задает форму кривой распределения шума квантования таким образом, что большая ее часть выходит за пределы этой полосы пропускания, как это показано на рисунке (в).
В методе избыточной дискретизации типичное значение коэффициента избыточности составляет 256 и более. Применяя обработку, обеспечивающую оптимальное формирование спектра шума, можно достичь разрешения в 18 бит и более при 1-разрядном преобразователе (1-разрядный АЦП – обыкновенный аналоговый компаратор).
Отличительной чертой 1-разрядного АЦП по сравнению с многоразрядными преобразователями является то, что в нем одни и те же аналоговые компоненты используются многократно в течение интервала времени между появлением выборок на выходе. Аналоговое входное напряжение преобразуется в цифровые биты по принципу повторного использования компонентов снова и снова, а не посредством применения различных элементов, относящихся к различным значениям, как это делается в многоразрядном преобразователе. Большая тактовая частота, с которой осуществляются повторения, позволяет достичь высокой точности, несмотря на разброс элементов компонентов.
Если посмотреть на сигнал, прошедший 1-разрядное преобразование, на частоте, равной частоте взятия выборок при избыточной дискретизации, то можно увидеть повышенную концентрацию двоичных единиц, когда аналоговый сигнал имеет большое значение, и повышенную концентрацию нулей, когда величина напряжения на входе мала.
На рисунке
Σ∆-АЦП представлена функциональная схема Σ∆-АЦП. Дифференциальный усилитель на входе непрерывно сравнивает входной сигнал с напряжением на выходе 1-разрядного ЦАП, который в типичном случае работает на частоте в 256 раз большей, чем требуемая частота окончательных выборок на цифровом выходе. Например, при частоте окончательных выборок 44,1 кГц тактовая частота внутренней избыточной дискретизации должна равняться 11,2896 МГц. Сигнал с выхода дифференциального усилителя интегрируется и подается на компаратор, а выходной сигнал компаратора стробируется с частотой избыточной дискретизации. Если сигнал на выходе интегратора больше 0 В, то на выходе компаратора идет поток двоичных единиц, а если оно меньше 0 В, то результатом будет последовательность нулей. Компаратор, по существу, является 1-разрядным АЦП, и он генерирует последовательность единиц и нулей в соответствии с результатом интегрирования выходного сигнала дифференциального усилителя.
Петля обратной связи замыкает путем подачи стробированного сигнала с выхода компаратора на вход 1-разрядного ЦАП. Это приводит к тому, что на выходе дифференциального усилителя возникает разность между мгновенным значением напряжения на аналоговом входе и средним значением аналоговых выборок, непосредственно предшествующих данному моменту времени. Петля ЦАП – дифференциальный усилитель – компаратор поддерживает нулевой заряд на конденсаторе интегратора. На стробированном выходе компаратора каждый раз появляется достаточное количество со значением «логическая 1», чтобы компенсировать заряд, поступивший в интегратор со стороны аналогового входа через дифференциальный усилитель. Другими словами, на выходе логического элемента И возникает поток битов, следующий с высокой частотой (в типичном случае – 11,2896 МГц), причем плотность логических единиц пропорциональна напряжению на аналоговом входе.
Чтобы выполнить преобразование потока битов в двоичное число, можно воспользоваться счетчиком и регистром-защелкой. На практике это выполняется с помощью цифрового фильтра нижних частот, на выходе которого вновь берутся выборки с частотой 44,1 кГц. Фильтр нижних частот сглаживает быстрые изменения в цифровом сигнале и, следовательно, осуществляет усреднение его по времени, подготавливая сигнал к тому, чтобы из него вновь могли быть взяты выборки с требуемой частотой. Эта процедура называется прореживанием или децимацией.
Дополнительный выигрыш, получаемый от применения избыточной дискретизации, состоит в том, что исключаются сложные аналоговые фильтры, необходимые для того, чтобы избежать перекрытия спектров.
Высокоскоростные средства обработки сигналов позволяют сделать преобразователи с избыточной дискретизацией не только более точными, чем многоразрядные схемы, но и более дешевыми, поскольку вместо трудно осуществимой точности значений параметров здесь требуется точность стробирования, а это значительно проще. Избыточная дискретизация в большой степени терпима к несовершенствам аппаратных средств. В общем случае, отпадает необходимость схемы выборки-хранения, поскольку частота преобразования входного сигнала исключительно велика по сравнению с частотой аналогового входного сигнала.
Недостатком сигма-дельта АЦП является то, что при скачкообразном изменении входного сигнала они начинают давать результат только через три – четыре отсчета.
Ряд ведущих фирм-производителей АЦП полностью перешли в области аналого-цифрового преобразования высокого разрешения на сигма-дельта АЦП. Эти АЦП имеют развитую цифровую часть, включающую микроконтроллер. Это позволяет реализовывать режимы автоматической установки нуля, самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.
С внедрением усовершенствованных АЦП и ЦАП различие между аналоговыми и цифровыми сигналами становится почти незаметным. Конечно, нужно позаботиться о том, чтобы избежать перекрестных искажений при взаимодействии аналоговой и цифровой частей в схеме, но преобразование сегодня все в большей степени сводится просто еще к одной интегральной микросхеме на печатной плате. Это способствует тому, что цифровая обработка сигналов применяется для выполнения все новых и новых функций в электронике.
Конвейерный АЦП
Конвейерный АЦП состоит из последовательного ряда каскадов, каждый из которых содержит АЦП низкого разрешения, ЦАП и усилитель. Они последовательно преобразуют аналоговый входной сигнал в цифровой, осуществляя конвейерную обработку данных. Конвейерные АЦП обычно применяются для энергоэффективного высокоскоростного преобразования широкополосных входных сигналов (например, в диапазоне 10…100 МГц). Частота выборки АЦП выбирается из того расчета, чтобы отношение OSR было малым (т.е. равнялось 2—4), а стандартное разрешение АЦП находится в диапазоне 8—14 бит.
Архитектура конвейерного АЦП является разомкнутой; собственная задержка составляет всего 4—6 циклов; имеется прямая связь между входным и выходным сигналами. Конвейерные АЦП, как правило, выполнены по КМОП-технологии с дискретной цепью (Discrete-Time, DT) переключаемого конденсатора (Switched Capacitor, SC). Конвейерному АЦП требуется нетривиальный аналоговый фильтр защиты от наложения спектров, который вносит свой вклад в энергопотребление и занимаемую площадь устройства.
Сигма-дельта АЦП
Эти АЦП значительно отличаются от конвейерных преобразователей и не допускают прямого использования некоторых стандартных характеристик. Сигма-дельта АЦП обеспечивают высокое соотношение ENOB/SNDR (например, до 10—12 и выше) при ширине полосы входного сигнала между низкой и средней (например, 100 кГц…10 МГц).
Σ/Δ-архитектура использует обратную связь между цифровой и аналоговой частями и высокое отношение OSR (например, 10—128). Высокое значение передискретизации позволяет использовать очень простые аналоговые фильтры защиты от наложения спектров, что экономит потребляемую энергию и занимаемую площадь. Однако при этом требуется дополнительная цифровая фильтрация. В результате использования петли обратной связи
Σ/Δ-АЦП могут быть неустойчивыми при больших входных сигналах и терять в производительности. По этой причине требуется установить диагностику перегрузки. Кроме того, в этих АЦП отсутствует прямая связь между входным и выходным сигналами, поэтому для характеристики работы АЦП часто вместо таких показателей как дифференциальная/интегральная нелинейность (Differential/Integral Non-Linearity, DNL/INL) используется динамический диапазон без паразитных составляющих (Spurious Free Dynamic Range, SFDR).
Рисунок 1 иллюстрирует архитектуры конвейерного и сигма-дельта АЦП.
Σ/Δ-АЦП выполнен в виде цепей с дискретным (Discrete Time, DT) и непрерывным временем (Continuous Time, CT). DT SC Σ/Δ-АЦП (дискретная цепь с переключаемым конденсатором) легко программируется на разные полосы частот, не требует калибровки и относительно нечувствительна к дрожанию тактовых импульсов, которые ухудшают производительность. Рассмотрим эти АЦП подробнее.

Рис. 1. Архитектуры конвейерного и сигма-дельта АЦП
SIGMA-DELTA ADC
Discusses key concepts converting analog signals to 8 channel delta-sigma ADCs in the single-mode and differential in the 16-bit MicroConverter 1874VE96T
СИГМА-ДЕЛЬТА АЦП В.П. Литвиненко, А.С. Тогушов, Н.П. Левкин
Рассматриваются ключевые понятия преобразования аналоговых сигналов в 8 канальном сигма-дельта АЦП в однопроводном и дифференциальном режимах в составе 16-разрядного микроконвертора 1874ВЕ96Т
Ключевые слова: интегральная схема, полная шкала, разрядность, дифференциальный вход
В этой статье представлен доработанный первый российский 16-разрядный микроконвертер 1874ВЕ96Т [1], разработанный в 2011 г. во ФГУП «НИИЭТ» г. Воронеж, на базе оригинального процессорного ядра с конвейерной обработкой данных и усовершенствованной архитектурой MCS-96, в который интегрированы стандартные процессорные ядра, флэш-память (16Кх16), модули генерации ШИМ, сторожевой таймер с использованием 8канального 16-разрядного сигма-дельта-АЦП с параллельным преобразованием и 14-разрядным высокоскоростным ЦАП с токовым выходом (2. 20 мА). ИС реализован на одном кристалле и имеет расширенный диапазон рабочих температур среды (-60^125) °С. Структурная схема ИС 1874ВЕ96Т показана на рис. 1.
Общие характеристики, особенности архитектуры, периферийные устройства микросхемы опубликованы в статье [1]. Данная статья посвящена работе 16-разрядного сигма-дельта-АЦП, встроенному в данный микроконвертер.
Сигма-дельта-АЦП состоят из сигма-дельтамодулятора и цифрового преобразователя — деци-мирующего цифрового фильтра. В данном типе АЦП преобразуемый сигнал сначала квантуется (в модуляторе), а затем дискретизируется (в преобразователе) [3].
Литвиненко Владимир Петрович — ВГТУ, канд. техн. наук, доцент, тел. (473) 271-44-57
Тогушов Александр Сергеевич — ВГТУ, инженер, тел. (473) 268-66-25
Левкин Николай Павлович — НИИЭТ, ведущий инженер, тел. 8-908-139-6299
Аналого-цифровые преобразователи конвертируют аналоговые напряжения на входе в цифровой эквивалент. Минимальное время преобразования составляет 16 мкс. Особенностью данного АЦП является возможность организации дифференциального режима включения входов.
Поскольку каждый преобразователь управляется независимо, то можно реализовать различные варианты включений, например: два АЦП — в режиме дифференциального включения, четыре — в режиме однополярных сигналов. Единственное условие, чтобы общее количество выводов, с которыми работают преобразователи, не превышало восьми.
АЦП имеет блок цифровых компараторов, позволяющих сравнивать результаты непрерывного аналого-цифрового преобразования с граничными условиями без использования ресурсов центрального процессора. Блок вырабатывает прерывания, если: результат преобразования больше заданной границы; результат преобразования меньше заданной границы; результат преобразования выходит за границы заданного диапазона; результат преобразования попадает в границы заданного диапазона. Все границы указываются в соответствующих регистрах. Цифровые компараторы объединены в группы по четыре, и каждый имеет свой приоритет. Для срабатывания компаратора с меньшим приоритетом необходимо, чтобы условие с большим приоритетом не сработало. Это позволяет на аппаратном уровне реализовывать сложные следящие алгоритмы.
В ходе разработке конструкции была проведена работа по унификации параметров сигма-дельта-АЦП, таких как SINAD (соотношение сиг-нал/шум+искажения), THD (общие гармонические искажения), коэффициент преобразования, напряжение диапазона преобразования АЦП, соотношения режимных параметров установленных и подтвержденных в ходе проведенных исследований ИС.
Высокая точность аналого-цифрового преобразования, осуществляемого в сигма-дельта-АЦП, обусловлена, прежде всего, возможностью получения высокой разрядности и линейности преобразования без применения многоуровневых пороговых устройств с эффективной фильтрацией преобразуемого сигнала.
Описания сигма-дельта-АЦП публикуются, в основном, фирмами-производителями. Ведущими в этой области является фирма Analog Devices. Ниже
приведены основные характеристики режимных параметров преобразования сигма-дельта-АЦП ИС 1874ВЕ96Т, с использованием юстированных определений и обозначений параметров, необходимых для потребителей, с учетом [2].
Структурная схема работы каналов приведена на рис.2.
Системный сигнал синхронизации поступает на тактовый вход АЦП и делится в 1, 2, 3, 4 или 5 раз для формирования внутреннего опорного тактового сигнала DMCLK, используемого для вычисления значений выборки.
Преобразуемый сигнал поступает на согласующую схему канала, обеспечивающую ограничение уровня и выбор полярности сигнала. Далее, сигнал поступает на усилитель с программируемым коэффициентом усиления, в диапазоне от 0 до 38 дБ, и, далее — на сигма-дельта модулятор с децима-тором. Цифровой фильтр выполняет две важные функции. Во-первых, это перемещение шума квантования за пределы требуемой полосы частот, который сформирован аналоговым модулятором, и, во-вторых, это прореживание потока битов высокой частоты до более низкой частоты 15-битных слов.
Сглаживающий прореживающий фильтр -это цифровой фильтр с характеристикой в форме sinc3, который понижает частоту дискретизации на значение, заданное в регистре управления. Делитель прореживания позволяет пользователю гибко подстроить значение выборки АЦП к требуемой программе контроллера.
Данные преобразования записываются в регистры результата с возможностью параллельного считывания через адресный порт и на блок компараторов.
В режиме дифференциального входа (дифф. вх.) напряжения на входах Июр и Ищ^- подаются в противофазе (со сдвигом на 180°) между собой и относительно опорного напряжения Икее в идеальном случае. Такой режим позволяет избавляться от синфазной помехи на входе АЦП. Передаточная характеристика в дифф. включении может быть показана прямыми Цда и (рис.3), при этом разность входных напряжений не должна превы-
шать диапазон преобразования иРзК
В режиме одиночного входа инверсный вход И^ отключается, а вместо него на вход АЦП аппаратно подается напряжение опорного источника
Передаточная характеристика каналов АЦП ИС 1874ВЕ96Т в любом режиме описывается в виде
АОС ~ (и№ ~ иіж) ‘ К0 ■> (1)
Бавс -выходной код АЦП, Иют -входное преобразуемое напряжение на позитивном входе АЦП, И^ — входное преобразуемое напряжение на негативном входе АЦП, Ко — коэффициент преобразования АЦП (тангенс угла наклона прямой преобразования). Передаточная характеристика АЦП приведена на рис. 3 сплошной линией.
>к Ва щс _ ( иют иіт! Ко
Входное напряжение начальной точки преобразования АЦП можно определить из выражения вида
ирз-,1 — напряжение первого межкодового перехода к коду 8001 И, Иьзв — шаг квантования. Входное напряжение в конечной точке преобразования АЦП при переходе к коду 7РРРИ равно:
Область значений входного напряжения АЦП, ограниченная (Ирэ- — ИРз+), является практическим диапазоном преобразования АЦП. Его можно определить из выражения вида
Коэффициент преобразования из выражения (1) можно определить из выражения вида
Кроа — коэффициент усиления АЦП (с диапазоном изменения от 0 до 38) дБ, К — коэффициент преобразования, определяемый конструкцией реализованной схемы. Для нашей схемы коэффициент К равен
Шаг квантования (единица младшего разряда) и единица старшего разряда определяются из выражений (7) — (9) соответственно:
N — число разрядов АЦП, иРзшп0т) — номинальный диапазон преобразования АЦП.
Зависимость диапазона преобразования Ирэя АЦП от величины опорного напряжения Икее при температуре (-60. +125) 0С приведена на рис. 4.
В процессе эксплуатации АЦП потребители должны руководствоваться вышеуказанной зависимостью, исходя из условий применения.
Внутренний источник опорного напряжения АЦП ИС выполнен с использованием напряжения запрещенной зоны полупроводника. Данное опорное напряжение через буфер подается на вывод REFCAP, на который подключается емкость фильтра, и подается к каналам АЦП. На данный вывод, при необходимости, подается внешний источник опорного напряжения UREF = (1,125^1,6) В.
Наиболее близким функциональным аналогом канала АЦП ИС 1874ВЕ96Т является микросхема AD73360 фирмы Analog Devices. Критерием оценки качества сигма-дельта-АЦП являются параметры SINAD и THD. При разработке ИС 1874ВЕ96Т получены те же шумовые показатели, что и у аналога, при этом отечественная микросхема имеет расширенный температурный диапазон и значительную скорость обработки результатов при параллельном преобразование АЦП и использовании ресурсов микроконвертера.
Вышеприведенное описание параметров сиг-ма-дельта-АЦП с четким определением и соотношениями параметров, соответствующих межгосударственному ГОСТ [2], позволяет однозначно предоставить широкому кругу потребителей не только принцип работы конкретного АЦП, но и любого преобразователя этого класса, а также научить грамотно применять все режимы работы схемы и полностью использовать её ресурсы.
1. Смерек В., Потапов И., Крюков В., Горохов В. Первый отечественный 16-разрядный микроконвертор на базе MCS-96.// электронные компоненты, №12, 2010.
2. ГОСТ 29109-91 «Микросхемы интегральные»// «часть 4. Интерфейсные интегральные схемы»: Изд-во Москва, 1992.
3. Голуб В. Сигма-дельта-модуляторы и АЦП.// Технология и конструирование в электронной аппаратуре, №4, 2003.
Воронежский государственный технический университет НИИЭТ, г. Воронеж
SIGMA-DELTA ADC V.P. Litvinenko, A.S. Togushov, N.P. Levkin
Discusses key concepts converting analog signals to 8 channel delta-sigma ADCs in the single-mode and differential in the 16-bit MicroConverter 1874VE96T
Key words: integrated circuit, full scale, bit, differential input
Сигма-дельта аналого-цифровой преобразователь
Когда требуется разрешение лучше 16 двоичных разрядов при высокой частоте выборок, рассматривавшиеся до сих пор методы преобразования становятся недостаточно эффективными, особенно при малых уровнях сигналов. Требование точно откалиброванного многоразрядного ЦАП в качестве элемента схемы преобразования становится чрезмерно жестким. Даже малые отклонения уровней на выходе ЦАП от их номинальных значений, обусловленные разбросом параметров и различное время срабатывания ключей могут привести к провалам в проходной характеристике и даже к пропуску отдельных двоичных комбинаций на выходе.
Скоростные цифровые схемы позволяют создавать преобразователи, действующие по принципу избыточной дискретизации и работающие с частотой выборок, значительно превосходящей теоретический минимум, определяемый шириной занимаемой сигналом полосы. Выгода от применения избыточной дискретизации заключается в том, что спектр шума квантования можно распределить по более широкому интервалу частот. Это дает возможность большую часть шума оставить вне зоны используемых частот при обратной фильтрации дискретизованного сигнала с сохранением компонентов только в полосе исходного сигнала.
Рассмотрим методику избыточной дискретизации с анализом в частотной области. Там, где преобразование постоянного напряжения имеет ошибку квантования до ½ младшего разряда (МЗР), дискретная система, работающая с переменным входным сигналом, обладает шумом квантования. Идеальный классический N-разрядный АЦП имеет среднеквадратичное значение шума квантования, равное h/
√12. Шум квантования равномерно распределен в пределах полосы Котельникова от 0 до fВ/2 (где h – значение младшего значащего бита и fв — частота дискретизации), как показано на рисуноке(а). Поэтому, его отношение сигнал/шум для полнодиапазонного синусоидального входного сигнала будет (6,02N+1,76)дБ. Если АЦП несовершенен и его реальный шум больше, чем его теоретический минимальный шум квантования, то эффективная разрешающая способность будет меньше, чем N-разрядов.
Если выбрать более высокую частоту дискретизации K fВ ( а),
Спектры шумов квантования в простом АЦП (а), АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (б) и Σ∆-АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (в)
то среднеквадратичное значение шума квантования остается h /√12, но шум теперь распределен по более широкой полосе от 0 до fВ /√12. Если затем использовать на выходе цифровой низкочастотный фильтр, то значительно уменьшится шум квантования, но сохранится полезный сигнал, улучшая таким способом эффективное число разрядов. Таким образом, выполняется аналого-цифровое преобразование с высоким разрешением при использовании аналого-цифрового преобразователя с низкой разрешающей способностью. Коэффициент K здесь упоминается, как коэффициент избыточной дискретизации. При этом необходимо отметить, что избыточная дискретизация дополнительно выгодна еще и тем, что она понижает требования к аналоговому ФНЧ.
Так как ширина полосы пропускания уменьшена выходным цифровым фильтром, скорость выдачи выходных данных может быть ниже, чем первоначальная частота дискретизации (KfВ), и при этом все же удовлетворять теореме Котельникова. Это достигается посредством передачи на выход каждого М-го результата и отбрасывания остальных результатов. Такой процесс называют децимацией с коэффициентом М. Несмотря на происхождение термина (decem по-латыни — десять), М может принимать любое целое значение, при условии, что частота выходных данных больше, чем удвоенная ширина полосы сигнала. Прореживание не вызывает никакой потери информации рисунок (б).
Если использовать избыточную дискретизацию только для улучшения разрешающей способности, необходимо применять коэффициент избыточности 2 2N , чтобы получить N- разрядное увеличение разрешающей способности. Сигма-дельта (Σ∆) преобразователь не нуждается в таком высоком коэффициенте избыточной дискретизации. Он не только ограничивает полосу пропускания сигнала, но также задает форму кривой распределения шума квантования таким образом, что большая ее часть выходит за пределы этой полосы пропускания, как это показано на рисунке (в).
В методе избыточной дискретизации типичное значение коэффициента избыточности составляет 256 и более. Применяя обработку, обеспечивающую оптимальное формирование спектра шума, можно достичь разрешения в 18 бит и более при 1-разрядном преобразователе (1-разрядный АЦП – обыкновенный аналоговый компаратор).
Отличительной чертой 1-разрядного АЦП по сравнению с многоразрядными преобразователями является то, что в нем одни и те же аналоговые компоненты используются многократно в течение интервала времени между появлением выборок на выходе. Аналоговое входное напряжение преобразуется в цифровые биты по принципу повторного использования компонентов снова и снова, а не посредством применения различных элементов, относящихся к различным значениям, как это делается в многоразрядном преобразователе. Большая тактовая частота, с которой осуществляются повторения, позволяет достичь высокой точности, несмотря на разброс элементов компонентов.
Если посмотреть на сигнал, прошедший 1-разрядное преобразование, на частоте, равной частоте взятия выборок при избыточной дискретизации, то можно увидеть повышенную концентрацию двоичных единиц, когда аналоговый сигнал имеет большое значение, и повышенную концентрацию нулей, когда величина напряжения на входе мала.
На рисунке
Σ∆-АЦП представлена функциональная схема Σ∆-АЦП. Дифференциальный усилитель на входе непрерывно сравнивает входной сигнал с напряжением на выходе 1-разрядного ЦАП, который в типичном случае работает на частоте в 256 раз большей, чем требуемая частота окончательных выборок на цифровом выходе. Например, при частоте окончательных выборок 44,1 кГц тактовая частота внутренней избыточной дискретизации должна равняться 11,2896 МГц. Сигнал с выхода дифференциального усилителя интегрируется и подается на компаратор, а выходной сигнал компаратора стробируется с частотой избыточной дискретизации. Если сигнал на выходе интегратора больше 0 В, то на выходе компаратора идет поток двоичных единиц, а если оно меньше 0 В, то результатом будет последовательность нулей. Компаратор, по существу, является 1-разрядным АЦП, и он генерирует последовательность единиц и нулей в соответствии с результатом интегрирования выходного сигнала дифференциального усилителя.
Петля обратной связи замыкает путем подачи стробированного сигнала с выхода компаратора на вход 1-разрядного ЦАП. Это приводит к тому, что на выходе дифференциального усилителя возникает разность между мгновенным значением напряжения на аналоговом входе и средним значением аналоговых выборок, непосредственно предшествующих данному моменту времени. Петля ЦАП – дифференциальный усилитель – компаратор поддерживает нулевой заряд на конденсаторе интегратора. На стробированном выходе компаратора каждый раз появляется достаточное количество со значением «логическая 1», чтобы компенсировать заряд, поступивший в интегратор со стороны аналогового входа через дифференциальный усилитель. Другими словами, на выходе логического элемента И возникает поток битов, следующий с высокой частотой (в типичном случае – 11,2896 МГц), причем плотность логических единиц пропорциональна напряжению на аналоговом входе.
Чтобы выполнить преобразование потока битов в двоичное число, можно воспользоваться счетчиком и регистром-защелкой. На практике это выполняется с помощью цифрового фильтра нижних частот, на выходе которого вновь берутся выборки с частотой 44,1 кГц. Фильтр нижних частот сглаживает быстрые изменения в цифровом сигнале и, следовательно, осуществляет усреднение его по времени, подготавливая сигнал к тому, чтобы из него вновь могли быть взяты выборки с требуемой частотой. Эта процедура называется прореживанием или децимацией.
Дополнительный выигрыш, получаемый от применения избыточной дискретизации, состоит в том, что исключаются сложные аналоговые фильтры, необходимые для того, чтобы избежать перекрытия спектров.
Высокоскоростные средства обработки сигналов позволяют сделать преобразователи с избыточной дискретизацией не только более точными, чем многоразрядные схемы, но и более дешевыми, поскольку вместо трудно осуществимой точности значений параметров здесь требуется точность стробирования, а это значительно проще. Избыточная дискретизация в большой степени терпима к несовершенствам аппаратных средств. В общем случае, отпадает необходимость схемы выборки-хранения, поскольку частота преобразования входного сигнала исключительно велика по сравнению с частотой аналогового входного сигнала.
Недостатком сигма-дельта АЦП является то, что при скачкообразном изменении входного сигнала они начинают давать результат только через три – четыре отсчета.
Ряд ведущих фирм-производителей АЦП полностью перешли в области аналого-цифрового преобразования высокого разрешения на сигма-дельта АЦП. Эти АЦП имеют развитую цифровую часть, включающую микроконтроллер. Это позволяет реализовывать режимы автоматической установки нуля, самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.
С внедрением усовершенствованных АЦП и ЦАП различие между аналоговыми и цифровыми сигналами становится почти незаметным. Конечно, нужно позаботиться о том, чтобы избежать перекрестных искажений при взаимодействии аналоговой и цифровой частей в схеме, но преобразование сегодня все в большей степени сводится просто еще к одной интегральной микросхеме на печатной плате. Это способствует тому, что цифровая обработка сигналов применяется для выполнения все новых и новых функций в электронике.
Сигма-дельта АЦП
Для проведения большинства измерений часто не требуется АЦП со скоростью преобразования, которую даёт АЦП последовательного приближения, зато необходима большая разрешающая способность. Сигма-дельта АЦП могут обеспечивать разрешающую способность до 24 разрядов, но при этом уступают в скорости преобразования. Так, в сигма-дельта АЦП при 16 разрядах можно получить частоту дискретизации до 100К отсчетов/сек, а при 24 разрядах эта частота падает до 1К отсчетов/сек и менее, в зависимости от устройства.
Обычно сигма-дельта АЦП применяются в разнообразных системах сбора данных и в измерительном оборудовании (измерение давления, температуры, веса и т.п.), когда не требуется высокая частота дискретизации и необходимо разрешение более 16 разрядов.
Принцип работы сигма-дельта АЦП сложнее для понимания. Эта архитектура относится к классу интегрирующих АЦП. Но основная особенность сигма-дельта АЦП состоит в том, что частота следования выборок, при которых собственно и происходит анализ уровня напряжения измеряемого сигнала, существенно превышает частоту появления отсчетов на выходе АЦП (частоту дискретизации). Эта частота следования выборок называется частотой передискретизации. Так, сигма-дельта АЦП со скоростью преобразования 100К отсчетов/сек, в котором используется частота передискретизации в 128 раз больше, будет производить выборку значений входного аналогового сигнала с частотой 12.8М отсчетов/сек.
Порядок модулятора определяется численностью интеграторов и сумматоров в его схеме. Сигма-дельта модуляторы N-го порядка содержат N сумматоров и N интеграторов и обеспечивают большее соотношение сигнал/шум при той же частоте отсчетов, чем модуляторы первого порядка. Примерами сигма-дельта модуляторов высокого порядка являются одноканальный AD7720 седьмого порядка и двухканальный ADMOD79 пятого порядка.
Наиболее широко в составе ИМС используются однобитные сигма-дельта модуляторы, в которых в качестве АЦП используется компаратор, а в качестве ЦАП – аналоговый коммутатор (рис. 6.13).
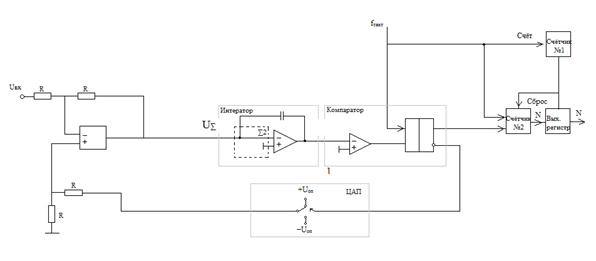
Рис. 6.13. Структурная схема сигма-дельта АЦП первого порядка
Входной сигнал поступает на инвертирующий вход дифференциального усилителя, а на неинвертирующий – выход одноразрядного ЦАП. Таким образом дифференциальный усилитель служит элементом сравнения (вычитающим устройством).
Интегратор – это активный аналоговый ФНЧ с высоким усилением в полосе частот входного сигнала и подавлением частотных составляющих, лежащих вне этой полосы. Квантователь – это в первом приближении компаратор с порогом срабатывания, равным “0”, выход которого может переключаться из состояния ”-Uоп” в состояние “+Uоп”, и который подключен ко входу синхронизируемого тактовой частотой (частотой дискретизации) элемента памяти, сохраняющего это состояние в течение тактового интервала. Если предположить, что на выходе этого элемента памяти, который одновременно является и выходом с уровнями модулятора должен формироваться цифровой сигнал соответствующий уровням логического “нуля” и “единицы” (АЦП), то таким элементом памяти может служить обычный D-триггер. В петле обратной связи при этом понадобится отдельное переключающее устройство, выполняющее функции ЦАП (на рис. 6.13 показано штриховой линией), который управляется цифровым сигналом, а на выходе формирует либо “-Uоп” либо “+Uоп”.
Дополнительным и очень важным достоинством сигма-дельта АЦП является то, что все его внутренние узлы могут быть выполнены интегральным способом на площади одного кремниевого кристалла. Это заметно снижает стоимость конечных устройств и повышает стабильность характеристик АЦП.
Итак, метод дельта-сигма-преобразования базируется на принципе нейтрализации входного тока (среднего) сигнала с помощью переключаемого внутреннего источника тока (иногда заряда в схеме с коммутируемым конденсатором). Это позволяет поддерживать нулевой средний ток на суммирующем входе ОУ. Это принцип уравновешения. Счетчик выслеживает число импульсов подключения к неинвертирующему входу в пределах некоторого заданного числа тактовых импульсов. Полученное число будет пропорционально среднему входному уровню, т.е. это и будет выходным кодом. В схеме рис. 6.13 такие импульсы тока сформированы с помощью эталонного напряжения (Uэт) и резисторов, подаваемые на неинвертирующий вход дифференциального усилителя.
Способ формирования многоразрядных отсчетов на выходе сигма-дельта модулятора зависит от того, какова требуется разрядность этих отсчетов и с какой скоростью они должны следовать. Повышение разрядности и скорости следования отсчетов (частоты дискретизации Fд) усложняет задачу и ограничивает выбор средств, с помощью которых эта задача может быть решена.
Наиболее простым способом получения многоразрядных отсчетов на выходе сигма-дельта модулятора является подсчет количества “единиц” в цифровом потоке, формируемом одноконтурным сигма-дельта модулятором 1-го порядка за период дискретизации Тд=1/Fд. Схема такого устройства представлена на рис. 6.13.
Если заданы частота дискретизации Fд и разрядность выходного кода m, то тактовая частота Fт, на которой работает сигма-дельта модулятор, должна быть выше частоты дискретизации в k раз: Fт=kFд, где k=2 m (при максимальном Uвх все разряды счетчика 2 должны быть установлены в “единицы”).
Тогда интервал времени равный периоду дискретизации можно сформировать путем деления тактовой частоты Fт на число k c помощью обычного счетчика (счетчик 1).
Описанный метод чрезвычайно прост, но обладает невысокой точностью и применим только для квантования медленно меняющихся процессов или в случае, когда высокой точности не требуется. Если же сигнал на входе преобразователя меняется быстро (следовательно, частота дискретизации должна быть велика) и необходимо получить высокое разрешение, то использование данного метода становится невозможным. В подобных случаях пользуются другими методами построения сигма-дельта АЦП – применением модуляторов 2-го и более высоких порядков, каскадным соединением таких модуляторов, использованием многоразрядных квантователей и многоразрядных ЦАП в петле обратной связи, а на выходе размещают сложные цифровые фильтры высоких порядков, выполняющие операцию децимации (прореживания) одноразрядного цифрового потока вместе с увеличением разрядности выходного кода.
Сигма-дельта АЦП
Недостатки АЦП многотактного интегрирования во многом устранены в конструкции сигма-дельта АЦП (в ранней литературе эти преобразователи назывались АЦП с уравновешиванием или балансом зарядов).
Своим названием эти преобразователи обязаны наличием в них двух блоков: сумматора (обозначение операции — S) и интегратора (обозначение операции — D). Один из принципов, заложенных в такого рода преобразователях, позволяющий уменьшить погрешность, вносимую шумами, а следовательно увеличить разрешающую способность — это усреднение результатов измерения на большом интервале времени.
Рис. 1.6 Блок-схема сигма-дельта модулятора
Основные узлы АЦП — это сигма-дельта модулятор и цифровой фильтр. Блок-схема n-разрядного сигма-дельта модулятора первого порядка приведена на рис. 1.6. Работа этой схемы основана на вычитании из входного сигнала Uвх(t) величины сигнала на выходе ЦАП, полученной на предыдущем такте работы схемы. Полученная разность интегрируется, а затем преобразуется в код параллельным АЦП невысокой разрядности. Последовательность кодов поступает на цифровой фильтр нижних частот.
Порядок модулятора определяется численностью интеграторов и сумматоров в его схеме. Сигма-дельта модуляторы N-го порядка содержат N сумматоров и N интеграторов и обеспечивают большее соотношение сигнал/шум при той же частоте отсчетов, чем модуляторы первого порядка.
Примерами сигма-дельта модуляторов высокого порядка являются одноканальный AD7720 седьмого порядка и двухканальный ADMOD79 пятого порядка.
![]()
Рис. 1.7 Структурная схема сигма-дельта АЦП
Наиболее широко в составе ИМС используются однобитные сигма-дельта модуляторы, в которых в качестве АЦП используется компаратор, а в качестве ЦАП — аналоговый коммутатор (рис. 1.7). Принцип действия пояснен в табл. 1. на примере преобразования входного сигнала, равного 0,6 В, при Uоп=1 В. Пусть постоянная времени интегрирования интегратора численно равна периоду тактовых импульсов. В нулевом периоде выходное напряжение интегратора сбрасывается в нуль. На выходе ЦАП также устанавливается нулевое напряжение. Затем схема проходит через показанную в табл. 1. последовательность состояний.
Таблица 1. Принцип работы сигма-дельта АЦП
В тактовые периоды 2 и 7 состояния системы идентичны, так как при неизменном входном сигнале Uвх=0,6 В цикл работы занимает пять тактовых периодов. Усреднение выходного сигнала ЦАП за цикл действительно дает величину напряжения 0,6 В:
Для формирования выходного кода такого преобразователя необходимо каким-либо образом преобразовать последовательность бит на выходе компаратора в виде унитарного кода в последовательный или параллельный двоичный позиционный код. В простейшем случае это можно сделать с помощью двоичного счетчика. Возьмем в нашем примере 4-разрядный счетчик. Подсчет бит на выходе компаратора за 16-титактный цикл дает число 13. Несложно увидеть, что при Uвх=1 В на выходе компаратора всегда будет единица, что дает за цикл число 16, т.е. переполнение счетчика. Напротив, при Uвх=-1 В на выходе компаратора всегда будет нуль, что дает равное нулю содержимое счетчика в конце цикла. В случае, если Uвх=0 то, как это видно из табл. 2, результат счета за цикл составит 810 или 10002. Это значит, что выходное число АЦП представляется в смещенном коде. В рассмотренном примере верхняя граница полной шкалы составит 11112 или +710, а нижняя — 00002 или -810. При Uвх=0,6 В, как это видно из левой половины табл. 1, содержимое счетчика составит 1310 в смещенном коде, что соответствует +5. Учитывая, что +8 соответствует Uвх=1 В, найдем
При использовании двоичного счетчика в качестве преобразователя потока битов, поступающих с выхода компаратора, необходимо выделять фиксированный цикл преобразования, длительность которого равна произведению Kсч fтакт. После его окончания должно производиться считывание результата, например, с помощью регистра-защелки и обнуление счетчика. В этом случае с точки зрения помехоподавляющих свойств сигма-дельта АЦП близки к АЦП многотактного интегрирования. Более эффективно с этой точки зрения применение в сигма-дельта АЦП цифровых фильтров с конечной длительностью переходных процессов.
С ростом числа каскадов интегрирования и суммирования в ??-модуляторе достигается лучший эффект при формировании кривой распределения шума квантования и лучшее эффективное число разрядов при фиксированном коэффициенте избыточной дискретизации. Блок-схема сигма-дельта АЦП второго порядка представлена на рис. 1.8.
Рис. 1.8 Блок-схема сигма-дельта модулятора второго порядка
Повышенная разрешающая способность может быть достигнута за счет увеличения коэффициента избыточной дискретизации и/или за счет использования модулятора более высокого порядка.
В сигма-дельта АЦП обычно применяются цифровые фильтры с амплитудно-частотной характеристикой (АЧХ) вида (sinx/x)3. Передаточная функция такого фильтра в z-области определяется выражением

где М — целое число, которое задается программно и равно отношению тактовой частоты модулятора к частоте отсчетов фильтра. (Частота отсчетов — это частота, с которой обновляются данные). Например, для АЦП AD7714 это число может принимать значения от 19 до 4000. В частотной области модуль передаточной функции фильтра

На рис. 1.9. приведен график амплитудно-частотной характеристики цифрового фильтра, построенной согласно выражению (*) при fтакт=38,4 кГц и М=192, что дает значение частоты отсчетов, совпадающей с первой частотой режекции фильтра АЦП, fотсч=50 Гц. Сравнение этой АЧХ с АЧХ коэффициента подавления помех АЦП с двухкратным интегрированием показывает значительно лучшие помехоподавляющие свойства сигма-дельта АЦП.
В то же время применение цифрового фильтра нижних частот в составе сигма-дельта АЦП вместо счетчика вызывает переходные процессы при изменении входного напряжения. Время установления цифровых фильтров с конечной длительностью переходных процессов, как следует из их названия, конечно и составляет для фильтра вида (sinx/x)3 четыре периода частоты отсчетов, а при начальном обнулении фильтра — три периода. Это снижает быстродействие систем сбора данных на основе сигма-дельта АЦП. Поэтому выпускаются ИМС AD7730 и AD7731, оснащенные сложным цифровым фильтром, обеспечивающие переключение каналов со временем установления 1 мс при сохранении эффективной разрядности не ниже 13 бит (так называемый Fast-Step режим). Обычно цифровой фильтр изготавливается на том же кристалле, что и модулятор, но иногда они выпускаются в виде двух отдельных ИМС (например, AD1555 — модулятор четвертого порядка и AD1556 — цифровой фильтр).
Рис. 1.9 АЧХ цифрового фильтра сигма-дельта АЦП
Сравнение сигма-дельта АЦП с АЦП многотактного интегрирования показывает значительные преимущества первых. Прежде всего, линейность характеристики преобразования сигма-дельта АЦП выше, чем у АЦП многотактного интегрирования равной стоимости. Это объясняется тем, что интегратор сигма-дельта АЦП работает в значительно более узком динамическом диапазоне, и нелинейность переходной характеристики усилителя, на котором построен интегратор, сказывается значительно меньше. Емкость конденсатора интегратора у сигма-дельта АЦП значительно меньше (десятки пикофарад), так что этот конденсатор может быть изготовлен прямо на кристалле ИМС. Как следствие, сигма-дельта АЦП практически не имеет внешних элементов, что существенно сокращает площадь, занимаемую им на плате, и снижает уровень шумов. В результате, например, 24-разрядный сигма-дельта АЦП AD7714 изготавливается в виде однокристалльной ИМС в 24-выводном корпусе, потребляет 3 мВт мощности и стоит примерно 14 долларов США, а 18-разрядный АЦП восьмитактного интегрирования HI-7159 потребляет 75 мВт и стоит около 30 долларов. К тому же сигма-дельта АЦП начинает давать правильный результат через 3-4 отсчета после скачкообразного изменения входного сигнала, что при величине первой частоты режекции, равной 50 Гц, и 20-разрядном разрешении составляет 60-80 мс, а минимальное время преобразования АЦП HI-7159 для 18-разрядного разрешения и той же частоты режекции составляет 140 мс.
В настоящее время ряд ведущих по аналого-цифровым ИМС фирм, такие как Analog Devices и Burr-Brown, прекратили производство АЦП многотактного интегрирования, полностью перейдя в области АЦ-преобразования высокого разрешения на сигма-дельта АЦП.
Сигма-дельта АЦП высокого разрешения имеют развитую цифровую часть, включающую микроконтроллер.
Это позволяет реализовать режимы автоматической установки нуля и самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.
Сигма-дельта АЦП
АЦП многотактного интегрирования имеют ряд недостатков.
Во-первых, нелинейность переходной статической характеристики операционного усилителя, на котором выполняют интегратор, заметным образом сказывается на интегральной нелинейности характеристики преобразования АЦП высокого разрешения. Для уменьшения влияния этого фактора АЦП изготавливают многотактными.
Другим недостатком этих АЦП является то обстоятельство, что интегрирование входного сигнала занимает в цикле преобразования только приблизительно третью часть. Две трети цикла преобразователь не принимает входной сигнал. Это ухудшает помехоподавляющие свойства интегрирующего АЦП.
В-третьих, АЦП многотактного интегрирования должен быть снабжен довольно большим количеством внешних резисторов и конденсаторов с высококачественным диэлектриком, что значительно увеличивает место, занимаемое преобразователем на плате и, как следствие, усиливает влияние помех.
Эти недостатки во многом устранены в конструкции сигма-дельта АЦП. Своим названием эти преобразователи обязаны наличием в них двух блоков: сумматора (обозначение операции — S) и интегратора (обозначение операции — D).
Один из принципов, заложенных в такого рода преобразователях, позволяющий уменьшить погрешность, вносимую шумами, а следовательно увеличить разрешающую способность — это усреднение результатов измерения на большом интервале времени.

Рисунок 20 Структурная схема сигма-дельта модулятора
Основные узлы АЦП — это сигма-дельта модулятор и цифровой фильтр. Схема n-разрядного сигма-дельта модулятора первого порядка приведена на рисунке 20.
Работа этой схемы основана на вычитании из входного сигнала Uвх(t) величины сигнала на выходе ЦАП, полученной на предыдущем такте работы схемы. Полученная разность интегрируется, а затем преобразуется в код параллельным АЦП невысокой разрядности. Последовательность кодов поступает на цифровой фильтр нижних частот.
Порядок модулятора определяется численностью интеграторов и сумматоров в его схеме. Сигма-дельта модуляторы N-го порядка содержат N сумматоров и N интеграторов и обеспечивают большее соотношение сигнал/шум при той же частоте отсчетов, чем модуляторы первого порядка.

Рисунок 21 Структурная схема сигма-дельта АЦП
Наиболее широко в составе ИМС используются однобитные сигма-дельта модуляторы, в которых в качестве АЦП используется компаратор, а в качестве ЦАП — аналоговый комутатор (рисунок 21).
Принцип действия пояснен в таблице 2 на примере преобразования входного сигнала, равного 0,6 В, при Uоп=1 В. Пусть постоянная времени интегрирования интегратора численно равна периоду тактовых импульсов. В нулевом периоде выходное напряжение интегратора сбрасывается в нуль. На выходе ЦАП также устанавливается нулевое напряжение. Затем схема проходит через показанную в таблице 2 последовательность состояний.
В тактовые периоды 2 и 7 состояния системы идентичны, так как при неизменном входном сигнале Uвх=0,6 В цикл работы занимает пять тактовых периодов. Усреднение выходного сигнала ЦАП за цикл действительно дает величину напряжения 0,6 В:

Для формирования выходного кода такого преобразователя необходимо каким-либо образом преобразовать последовательность бит на выходе компаратора в виде унитарного кода в последовательный или параллельный двоичный позиционный код. В простейшем случае это можно сделать с помощью двоичного счетчика. Возьмем в нашем примере 4-разрядный счетчик. Подсчет бит на выходе компаратора за 16-ти тактный цикл дает число 13. Несложно увидеть, что при Uвх=1 В на выходе компаратора всегда будет единица, что дает за цикл число 16, т.е. переполнение счетчика. Напротив, при Uвх=-1 В на выходе компаратора всегда будет нуль, что дает равное нулю содержимое счетчика в конце цикла. В случае, если Uвх=0 то, как это видно из табл. 2, результат счета за цикл составит 810 или 10002. Это значит, что выходное число АЦП представляется в смещенном коде. В рассмотренном примере верхняя граница полной шкалы составит 11112 или +710, а нижняя — 00002 или -810. При Uвх=0,6 В, как это видно из левой половины табл. 2, содержимое счетчика составит 1310 в смещенном коде, что соответствует +5. Учитывая, что +8 соответствует Uвх=1 В, найдем

При использовании двоичного счетчика в качестве преобразователя потока битов, поступающих с выхода компаратора, необходимо выделять фиксированный цикл преобразования, длительность которого равна произведению Kсч fтакт. После его окончания должно производиться считывание результата, например, с помощью регистра-защелки и обнуление счетчика. В этом случае с точки зрения помехоподавляющих свойств сигма-дельта АЦП близки к АЦП многотактного интегрирования. Более эффективно с этой точки зрения применение в сигма-дельта АЦП цифровых фильтров с конечной длительностью переходных процессов.

В сигма-дельта АЦП обычно применяются цифровые фильтры с амплитудно-частотной характеристикой (АЧХ) вида . Передаточная функция такого фильтра в z-области определяется выражением:

где М — целое число, которое задается программно и равно отношению тактовой частоты модулятора к частоте отсчетов фильтра. (Частота отсчетов — это частота, с которой обновляются данные). В частотной области модуль передаточной функции фильтра:

На рис. 22 приведен график амплитудно-частотной характеристики цифрового фильтра, построенной согласно выражению (13) при fтакт=38,4 кГц и М=192, что дает значение частоты отсчетов, совпадающей с первой частотой режекции фильтра АЦП, fотсч=50 Гц. Сравнение этой АЧХ с АЧХ коэффициента подавления помех АЦП с двухкратным интегрированием показывает значительно лучшие помехоподавляющие свойства сигма-дельта АЦП.

В то же время применение цифрового фильтра нижних частот в составе сигма-дельта АЦП вместо счетчика вызывает переходные процессы при изменении входного напряжения. Время установления цифровых фильтров с конечной длительностью переходных процессов, как следует из их названия, конечно и составляет для фильтра вида четыре периода частоты отсчетов, а при начальном обнулении фильтра — три периода. Это снижает быстродействие систем сбора данных на основе сигма-дельта АЦП.

Рисунок 22 АЧХ цифрового фильтра сигма-дельта АЦП
Сравнение сигма-дельта АЦП с АЦП многотактного интегрирования показывает значительные преимущества первых.
Прежде всего, линейность характеристики преобразования сигма-дельта АЦП выше, чем у АЦП многотактного интегрирования равной стоимости. Это объясняется тем, что интегратор сигма-дельта АЦП работает в значительно более узком динамическом диапазоне, и нелинейность переходной характеристики усилителя, на котором построен интегратор, сказывается значительно меньше. Емкость конденсатора интегратора у сигма-дельта АЦП значительно меньше (десятки пикофарад), так что этот конденсатор может быть изготовлен прямо на кристалле ИМС. Как следствие, сигма-дельта АЦП практически не имеет внешних элементов, что существенно сокращает площадь, занимаемую им на плате, и снижает уровень шумов.
Сигма-дельта АЦП высокого разрешения имеют развитую цифровую часть, включающую микроконтроллер. Это позволяет реализовать режимы автоматической установки нуля и самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.
На базе преобразователей напряжение-частота (ПНЧ) могут быть построены интегрирующие АЦП, обеспечивающие относительно высокую точность преобразования при низкой стоимости. Существует несколько видов ПНЧ. Наибольшее применение нашли ПНЧ с заданной длительностью выходного импульса. Структурная схема такого ПНЧ приведена на рис. 23.
Работает ПНЧ следующим образом. Под действием положительного входного сигнала Uвх напряжение Uи на выходе интегратора И уменьшается. При этом ключ S разомкнут. Когда напряжение Uи уменьшится до нуля, компаратор К переключается, запуская тем самым одновибратор. Одновибратор формирует импульс стабильной длительности Ти, который управляет ключем. Последовательность этих импульсов является выходным сигналом ПНЧ. Ключ замыкается и ток Iоп в течение Ти поступает на вход интегратора, вызывая увеличение выходного напряжения интегратора. Далее описанный процесс снова повторяется.

Рисунок 23 Структурная схема ПНЧ
Импульсы тока Iоп уравновешивают ток, вызываемый входным напряжением Uвх. В установившемся режиме


где Uвх.ср — среднее значение входного напряжения за период Т.

Рисунок 24 Блок-схема АЦП на основе ПНЧ
Таким образом, по существу ПНЧ преобразует входное напряжение в унитарный код. Для его преобразования в двоичный позиционный можно использовать счетчик. Схема интегрирующего АЦП на базе ПНЧ приведена на рис. 24.
Двоичный счетчик подсчитывает число импульсов, поступивших от ПНЧ за период Тотсч=1/fотсч, задаваемый отсчетными импульсами, которыми содержимое счетчика заносится в выходной регистр-защелку. Вслед за этим происходит обнуление счетчика. Число импульсов n, подсчитанных счетчиком за время Тотсч,

Здесь Uвх.ср — среднее значение входного напряжения за весь период Тотсч.
Можно заметно повысить точность ПНЧ, если вместо одновибратора включить тактируемый импульсами стабильной частоты D-триггер. Несложно убедиться (см. рис. 16), что в этом случае ПНЧ превращается в однобитный сигма-дельта модулятор.




