Колебательный контур ― это электрическая цепь, содержащая катушку индуктивности и конденсатор. В такой электрической цепи происходят колебания электрического тока и напряжения, и взаимная трансформация энергии электрического поля и энергии магнитного поля.
Процессы в колебательном контуре У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.
Если в цепи, кроме проводов и резисторов, находится катушка индуктивности, в равномерный и быстрый процесс перераспределения заряда вмешивается ЭДС самоиндукции катушки. Согласно правилу Ленца, втекающий в катушку ток вызывает ЭДС самоиндукции ― а ЭДС самоиндукции создает индуцированный ток, направленный так, чтобы препятствовать изменению тока в цепи. Если ток в цепи вдруг резко увеличивается ― индукционный ток стремиться его уменьшить, если ток в сети вдруг уменьшается ― индукционный ток стремиться его увеличивать.
Поэтому из―за катушки индуктивности заряд не переходит сразу через всю цепь, от одной обкладки конденсатора к другой. Сила тока в цепи медленно увеличивается ― потому что ее быстрому росту препятствует ЭДС самоиндукции катушки. Максимальной сила тока становится в тот момент, когда конденсатор разряжен (обе его обкладки обладают нулевым зарядом). В этот момент сила тока максимальна благодаря тому, что как только ее перестает наращивать конденсатор за счет потерянных зарядов ― ЭДС самоиндукции прекращает ей препятствовать.
Но разряженный конденсатор больше не может поддерживать силу току ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.
После того как конденсатор зарядиться ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.
Что такое РЕЗОНАНС НАПРЯЖЕНИЙ | САМОЕ ПОНЯТНОЕ объяснение
Колебания
Начнём обсуждение этой темы с колебаний. В обычной жизни мы часто слышим это слово: «цветок колеблется на ветру», «я не могу принять решение, колеблюсь», «температура воздуха колеблется в диапазоне…». Но что такое колебания в физике?
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
Попробуйте привести несколько примеров такого движения. Верно, к колебаниям можно отнести движение стрелки, вращение качели, качание маятника часов.
Колебания бывают вынужденными и свободными.
- Вынужденные колебания — это колебания, происходящие под действием внешней периодически меняющейся силы. Посадите свою маленькую сестрёнку или братишку на качели: раскачивая их, вы станете той самой внешней силой, под действием которой качели движутся, совершая при этом вынужденные колебания.
- Свободные колебания — это колебания, происходящие под действием внутренних сил в колебательной системе. Груз колеблется на нити или пружине — вот самый распространённый пример свободных колебаний. Такие колебания всегда затухающие, потому что ни у одной системы нет бесконечного запаса энергии для такого движения: рано или поздно колебание прекратится.
Что может совершать свободные колебания? Математический (груз + нить) и пружинный (груз + пружина) маятники, а также электромагнитные волны.

Электромагнитные волны
В курсе школьной физики 8-го класса вы изучали отдельно главы про электричество и магнетизм, и только в 9–10-х классах узнали, что такое разделение не совсем верно. Дело в том, что электричество и магнетизм — две стороны одной монеты, они не могут существовать друг без друга. Движущееся электрическое поле порождает магнитное, а движущееся магнитное поле порождает электрическое. Эти поля распространяются в пространстве одновременно и, что удивительно, в разных плоскостях. Взгляните на рисунок!
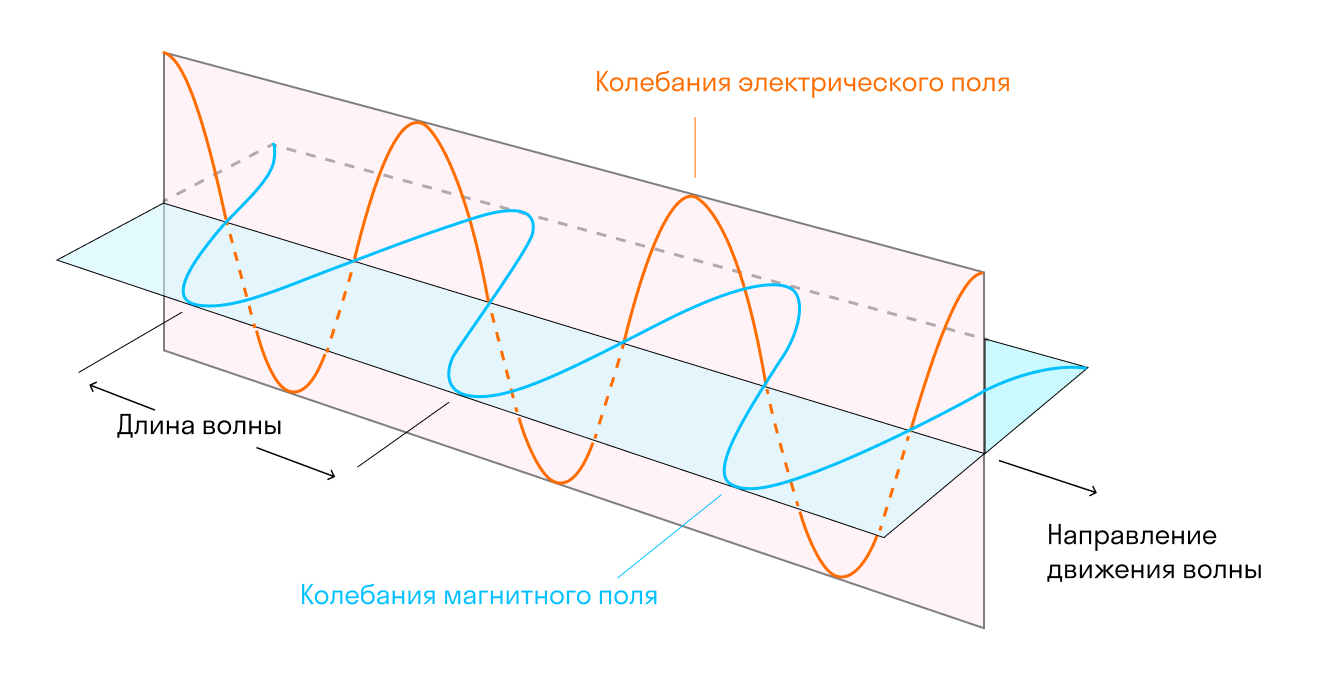
Электромагнитные волны — это распространение в пространстве с течением времени переменных (вихревых) электрических и магнитных полей.
Вихревым электрическим полем называется поле, силовые линии которого представляют собой замкнутые линии.
В разрезе этой темы стоит запомнить две фамилии: Максвелл и Герц. Вот увидите, как сойдёт с ума от счастья учитель физики, когда вы их назовёте. Джеймс Максвелл описал основные положения электромагнитной теории, а Генрих Герц доказал существование электромагнитных волн опытным путём.
К электромагнитным волнам относятся радио, Wi-Fi и даже свет. Более подробно об этом можно прочесть в нашей статье.

Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных параметров. Онлайн калькулятор резонансной частоты колебательного контура, добротности и коэффициента затухания в зависимости от величин индуктивности, ёмкости и сопротивления потерь
Колебательный контур – это пассивная электрическая цепь, которая состоит из конденсатора и катушки индуктивности, в которой возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный контур называется последовательным.
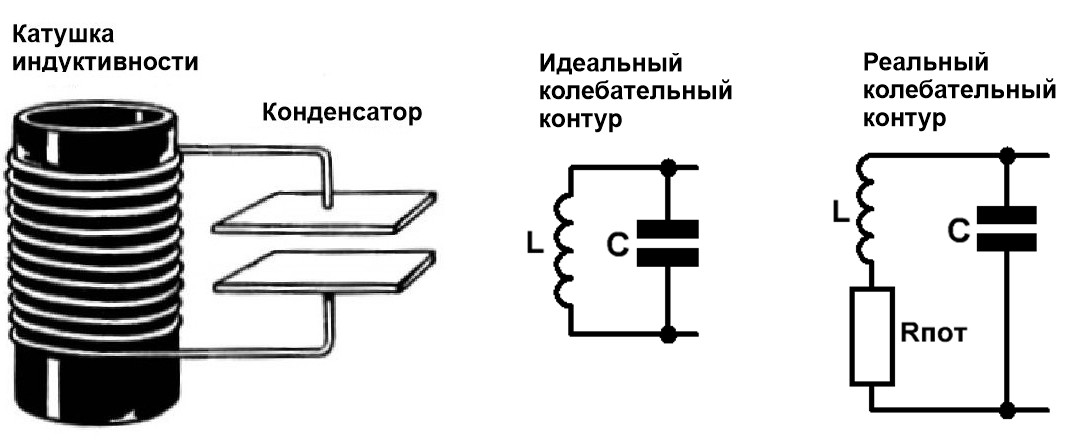
Для начала давайте рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного.
Рис.1 Параллельный колебательный контур, его изображение на схеме
(идеальный колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного сопротивления потерь катушки – Rпот . Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
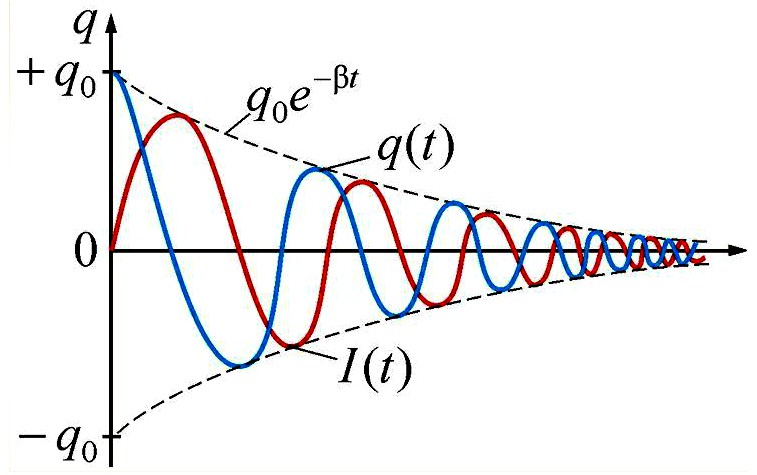
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд qmax от внешнего источника Bat напряже- нием Umax . После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь, суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
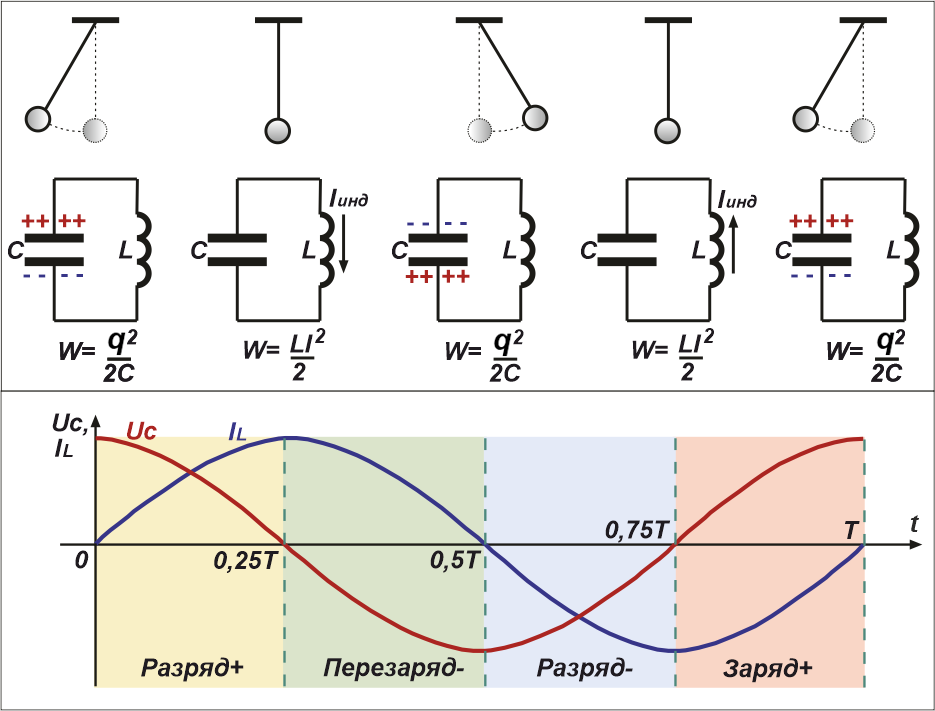
Рис.3 Фазы колебаний в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна W = q 2 /2C ). Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС самоиндукции, препятствующая этому росту.
2. t = 0.25Т – конденсатор полностью разряжен. Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки W = L*I 2 /2 . Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0.5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0.75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь: Формулы для расчёта колебательного LC контура:
Период колебаний: T0 = 2π√ LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 = 2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура: ;
Мгновенные значения напряжения, тока и энергии рассчитываются по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров (с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания β и логарифмический декремент колебаний λ .
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно пропорциональная времени τ , по истечении которого амплитуда колебаний убывает в е раз. Для колебательного контура данная величина вычисляется по формуле: β = Rпотерь /(2L) .
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент равен коэффициенту затухания, умноженному на период колебаний: λ = βT .
С учётом коэффициента затухания формулы приобретают следующий вид:
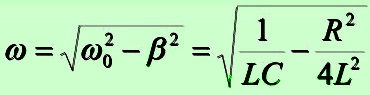
Заряд: q(t) = qmax cos(ωt) e (-βt) ;
Напряжение: U(t) = Umax cos(ωt) e (-βt) ;
Сила тока: I(t) = Imax sin(ωt) e (-βt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) ;
Период: ;
Круговая (циклическая) частота: ;
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие β 2 2 , круговая частота контура равна ω ≈ ω0 , а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
Расчёт резонансной частоты, добротности и коэффициента
затухания контура
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.
Колебательный контур
Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.
Колебательный контур состоит из конденсатора и катушки индуктивности. Электроёмкость конденсатора — (C), индуктивность катушки — (L).
Изображение на схемах
Обрати внимание!
В колебательном контуре периодически происходит переход энергии электрического поля в энергию магнитного поля и наоборот.
На некоторое время с помощью переключателя зарядим конденсатор, замкнув его на источник тока ( рис. А ). Затем наш заряженный конденсатор подсоединим к катушке ( рис. Б ).


t 1 = T 4 . Заряженный конденсатор, подключённый к катушке, начнёт через неё разряжаться. Нижняя обкладка заряжена положительно. Разрядный ток, проходящий по катушке, создаст вокруг неё магнитное поле. Явление самоиндукции будет препятствовать резкому возрастанию тока через катушку, поэтому ток растёт постепенно и через некоторое время приобретает максимальное значение. В этот момент конденсатор будет полностью разряжен. Произошло превращение энергии электрического поля в энергию магнитного поля.

2t 1 = T 2 . Так как конденсатор разряжен, то в следующий момент времени ток должен мгновенно исчезнуть, но в результате самоиндукции, которая препятствует убыванию тока, он некоторое время поддерживается в цепи. Индукционный ток сонаправлен с уходящим током цепи и благодаря этому конденсатор заряжается, только заряд на обкладках поменяется на противоположный знак. Энергия магнитного поля перешла в энергию электрического поля.
Если рассматривать идеальную модель колебательного контура, который не имеет сопротивления, то энергия в нём не потратится, и конденсатор вновь зарядится до максимального значения. В реальности такого не бывает, потому что часть энергия уйдёт на преодоление сопротивления проводников и превратится в тепловую энергию. В реальном колебательном контуре в этот момент времени конденсатор зарядится уже не полностью.


За промежуток времени 4t 1 произошло одно полное колебание. Значит, 4t 1 (=T) , где (T) — период колебаний.
Принцип действия колебательного контура
Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.
Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.
Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.
Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.
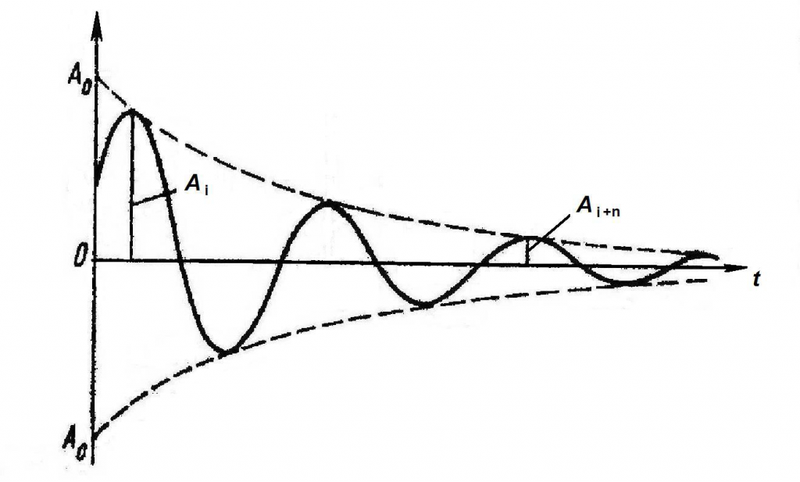
Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.
Резонанс LC-контура
Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).
Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:
Еще термины по предмету «Электроника, электротехника, радиотехника»
Полная мощность рассеивания затвора (Gate power dissipation)
мощность, передаваемая от системы управления преобразователя на управляющие выводы затвора, с учетом перезаряда входной и обратной проходной емкостей и частоты коммутации.
Положительный электрод
для устройства, имеющего два электрода, этот электрод имеет более высокий эпектрический потенциал; в некоторых спучаях, например, дпя электронных ламп и полупроводниковых устройств термин «положительный электрод» применяют для одного или другого электрода в зависимости отусловия электрического оперирования устройства; в других спучаях (например, для эпектрохимическихэлементов) термин «положительный электрод» относят к определенному электроду.
Табличный функциональный преобразователь (LUT, Look-Up Table)
логический блок программируемых БИС/СБИС, реализованный на основе схем программируемой памяти.
- Собственная частота колебательного контура
- Контур
- Виброметр колебательной мощности
- Колебательная составляющая свободного тока
- Четкость контура
- Холодильный контур
- Водяной контур
- Контур протектора
- Контур управления
- Контур Бюргерса
- Информационный контур
- Исходный контур
- Контур ситуации
- Автонастройка контура
- Контур связи
- Контур цепи
- Матрица контуров
- Резонансный контур
- Согласованные контуры
- Контур газоносности
Повышай знания с онлайн-тренажером от Автор24!
- Напиши термин
- Выбери определение из предложенных или загрузи свое
- Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек
Все самое важное и интересное в Telegram
Все сервисы Справочника в твоем телефоне! Просто напиши Боту, что ты ищешь и он быстро найдет нужную статью, лекцию или пособие для тебя!
Перейти в Telegram Bot
Подписаться через qr-код
Telegram Bot
- Научные статьи
- Лекторий
- Методические указания
- Справочник терминов
- Статьи от экспертов
- Отзывы об Автор24
- Последние статьи
- Помощь эксперта
- Справочник рефератов
- Нейросеть для решения задач
- Нейросеть для написания реферата
- Поиск репетитора
- Для правообладателей
- Работа для преподавателей
- Работа для репетиторов
- Партнерская программа
- Реклама на сайте

Возможность создать свои термины в разработке
Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️
Включи камеру на своем телефоне и наведи на Qr-код.
Кампус Хаб бот откроется на устройстве
Привет! Рады, что термин оказался полезен
Для копирования текста подпишись на Telegram bot. Удобный поиск по учебным материалам в твоем телефоне
Последовательный колебательный контур
В колебательном контуре можно получить незатухающие колебания, если подключить его к источнику переменного тока.
Если источник подключен последовательно с катушкой L и конденсатором С , то такая цепь называется последовательным колебательным контуром ( рис.3 ).
При подключении внешнего источника к контуру в нем возникают не собственные (свободные) колебания контура, которые определяются значениями L и C , а с частотой напряжения источника U=Um∙sinω∙t .
Такие колебания контура называются вынужденными .
При вынужденных колебаниях элементы контура L, C будут иметь, в зависимости от частоты источника, определенные индуктивное XL и емкостное Xc сопротивления и соответствующие падения напряжения UL, Uc на них.
Но контур имеет не только реактивные сопротивления, а еще и активное cопротивление потерь R , которое в основном равно сопротивлению провода катушки.
Так как в катушке и конденсаторе напряжения сдвинуты относительно тока на разные фазовые углы, то более наглядно их можно показать на векторных диаграммах ( рис.4 )
Напряжение на индуктивном сопротивлении UL опережает ток на 90° , а напряжение на емкостном сопротивлении Uc отстает от тока на такой же угол 90° И получается, что векторы UL и Uc сдвинуты между собой на 180° , т.е. находятся в противофазе.
Вектор напряжения на источнике U будет равен геометрической сумме напряжения вектора UR и вектора разницы напряжений реактивных сопротивлений UL-Uc .
Как видно из диаграммы рис.4а при UL > Uc напряжение внешнего источника опережает ток в колебательном контуре на угол φ и находится выше оси абcцисс в зоне напряжений индуктивности. Значит в данном случае контур имеет сопротивление индуктивного характера.
При UL ( рис.4b ) вектор источника уже будет отставать от вектора тока на угол φ и контур будет иметь емкостное сопротивление.
Полное сопротивление контура Z будет равно:
Амплитудное значение тока Im определяется по формуле:
где Um — амплитудное напряжение источника, а ω -его угловая частота.
При выполнении равенства:
XL=Xc,
получается наибольшее значение тока и имеет место явление, которое называется резонансом .
Резонанс возникает при условии совпадения частоты источника напряжения с собственной частотой колебания контура.
На рис.5 показан график характеристик зависимости тока Iк и полного сопротивления Z последовательного контура от частоты.

Чтобы понять природу электрического резонанса рассмотрим механический резонанс.
Явление резонанса можно наблюдать на опыте как показано на рис.6 .
Здесь на натянутой общей нитке привязаны три пары шаров 1-1′, 2-2′, 3-3′ каждый из которых представляет собой маятник.
Если раскачать рукой шар 1 , то начинает раскачиваться и шар 1 ‘, тогда как все другие шары остаются неподвижными. Точно так же, если раскачать шар 3 , начнет раскачиваться только шар 3 .
Этот механический резонанс объясняется следующим образом.
В нашем опыте собственные частоты каждой пары маятников одинаковы, т.к. шары одинаковые и длина их нитей тоже одинакова.
Раскачиваясь, маятник 1 передает по общей нитке свои колебания остальным маятникам. Но эти колебания раскачивают только маятник 1′ потому, что его частота собственных колебаний совпадает с частотой «толчков» общей нити от маятника 1 . Так как эти «толчки» совпадают с тактом собственной частоты маятника 1′ , то его амплитуда раскачивания все больше и больше возрастает и может стать больше амплитуды раскачивающего маятника 1 .
Так же, примерно, происходит и при электрическом резонансе.
Представим себе маятник 1 источником колебаний, а маятник 1′ — колебательным контуром.
Маятник 1 , допустим, будет качаться с постоянной амплитудой и частотой.
Маятник 1′ не сможет сразу достичь амплитуды и частоты маятника 1 потому, что раскачать мгновенно общую нить до резонансной частоты и амплитуды будут мешать различные тормозящие процессы — сопротивление воздуха, инерционность, провис нити и т.д. Это будет выглядеть как торможение тока контура индуктивным и емкостным сопротивлениеми при несовпадении частоты источника и контура.
С течением времени маятник 1 раскачает маятник 1′ до своей частоты и амплитуды. Начнется процесс резонанса.
Амплитуда маятника 1′ будет расти до какого то значения, пока сила «подталкивания» не уравновесится противоположной силой торможения.
Так же и в контуре резонансный ток не может возрастать бесконечно.
При резонансе амплитуда тока в контуре равна:
Напряжение на индуктивном сопротивлении —
на емкостном сопротивлении —
Tак как XL=Xc , то вектора UL и Uc будут равны (UL=Uc) , но противоположно направлены ( рис.7 ).
Вектор напряжения U источника совпадает с вектором тока I и равен по величине напряжению на активном сопротивлении UR .
Отсюда следует, что при резонансе контур оказывает источнику сопротивление активного характера R который не дает амплитуде напряжения Um увеличиваться до бесконечности:
При резонансе отношение между напряжением на индуктивном сопротивлении и напряжением источника будет равно добротности Q катушки:
А добротность контуров, применяемых в радиотехнике, большая. Поэтому напряжение на катушке может превышать в сотни раз напряжение источника.
Но так как при резонансе напряжение на катушке равно напряжению на конденсаторе, значит отношение напряжения на конденсаторе к напряжению источника тоже будет равно добротности:
Для примера на рис.8 показана схема последовательного контура с реальными значениями элементов схемы и параметров, а так же полученные величины напряжений на этих элементах. Отсюда видно, что напряжение на катушке и конденсатотре при резонансе будет больше напряжения источника в Q раз.
Резонанс в последовательном колебательном контуром называют резонансом напряжения, т.к. напряжение на реактивных элементах при резонансе становится больше напряжения внешнего источника.
Способность колебательного контура создавать интенсивные колебания на одной частоте (точнее в узкой полосе частот) и почти не реагировать на сигналы других частот называется избирательностью.
Избирательность S численно показывает во сколько раз ослабляются посторонние сигналы по сравнению с колебаниями резонансной частоты ( рис.9 ):
где I(▲f) — ток в контуре при расстройки контура на ▲f .
Полосой пропускания контура называют полосу частот, в пределах которой ток в контуре уменьшается не более, чем в заданное число раз по сравнению с током при резонансе ( рис.10 ):
где — k коэффициент пропорциональности, указывающий на каком уровне резонансного тока Ip измеряется полоса пропускания.
Для k=1 — уровень Ik = 0,707·Ip и
k=√3 — уровень Ik = 0,5·Ip и
В электрических схемах колебательный контур связан с источником сигнала разными способами — непосредственно, индуктивною или емкостной связью.
Если контур связан с источником И индуктивно ( рис.11 ), то контур будет являтся последовательным, т.к. в катушке колебательного контура индуктируется ЭДС, что равносильно последовательному включению источника с L и С .
Такая связь применяется в радиоприемниках для связи антенны с контуром( рис.12 ).
С помощью конденсатора переменной емкости можно настраивать контур в резонанс с нужной радиостанцией.
В этом случае контурный ток, вызванный сигналом этой радиостанции, становится относительно большим, в то время как контурные токи, вызванные другими станциями, ничтожно малы.
Напряжение между точками a — b , вызванное большим резонансным током, подается к следующим каскадам приемника.
Параллельный колебательный контур
В параллельном колебательном контуре источник сигнала соединен с катушкой индуктивности и конденсатором параллельно (рис.11).
При подаче переменного напряжения на контур происходит обмен энергиями между конденсатором и катушкой, но только в цепи внутри контура.
Для возникновения резонанса в нем, как и в последовательном контуре, необходимыми условиями являются равенство емкостного Хс и индуктивного ХL сопротивлений, а так же равенство частоты собственных колебаний контура и частоты колебаний источника тока.
Только резонанс в параллельном колебательном контуром, в отличии от резонанса в последовательном контуре, называют резонансом тока.
В идеальном параллельном контуре (без потерь) вектора индуктивного Ic и емкостного тока IL (при ХL=Xc ) при резонансе будут направлены в противоположные стороны и суммарный ток будет обращаться в нуль ( рис.14a ). А это значит, что сопротивление контура будет стремится к бесконечности.
Но в реальном параллельном контуре существует сопротивление потерь R которое сосредоточено в основном в индуктивности ( рис 14b ) и поэтому, даже при резонансе ток в контуре уже не равен нулю, а равен активной составляющей тока в цепи катушки — Iк=IL+IR.
Значит полное сопротивление контура Z будет уже не бесконечно, а равно:
На рис.15 показан график характеристик зависимости тока Iк и полного сопротивления Z параллельного контура от частоты.
Можно сделать вывод: в цепи параллельного контура существуют два тока — ток от источника I протекающий через активное сопротивление потерь катушки и реактивный ток контура Iк .
Внутри контура протекают реактивный ток довольно таки большой величины:
но он потребляет малый ток от источника, который необходим лишь для компенсации потерь в контуре:
Добротность Q параллельного контура, в отличии от последовательного контура, показывает во сколько раз ток в элементах контура больше потребления тока источника:
На рис.16 дан конкретный пример параллельного колебательного контура, где видно, что ток контура больше тока источника в Q раз.
В радиоприемниках так же применяется непосредственная связь колебательного контура с антенной, т.е. контур включен параллельно источнику сигнала ( рис.17 ).
Переменным конденсатором настраиваем контур на частоту сигнала нужной радиостанции. При резонансе контурный ток, вызванный нужной радиостанцией, становится относительно большим, а сопротивление контура тоже большим.Поэтому между точками а и b получается значительное напряжение.
Для других станций контур представляет малое сопротивление и сигнал радиостанции уходит в «землю».




