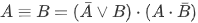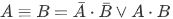Отрицанием высказывания A называется новое высказывание «не A», принимающее значение «истина», если A ложно, и значение «ложь», если A истинно.
A
Правило отрицания высказываний с кванторами: $ mathrm< overline<(forall x)A(x)>=(exists x)overline, overline<(exists x)A(x)>=(forall x)overline > $
Расшифровка первого правила: высказывание «неверно, что для любого x выполняется A(x)» совпадает с высказыванием «найдётся x, для которого A(x) не выполняется».
Расшифровка второго правила: высказывание «неверно, что найдётся x, для которого выполняется A(x)» совпадает с высказыванием «для любого x A(x) не выполняется».
п.2. Конъюнкция
Конъюнкция двух высказываний – это высказывание, которое будет истинным, если истинны оба исходных высказывания; а во всех остальных случаях – будет ложным.
Конъюнкция является логическим умножением.
Обозначение конъюнкции A ∧ B, читается «А и В». Таблица истинности:
A
B
A ∧ B
С точки зрения операций над множествами, конъюнкция аналогична пересечению двух множеств (см. §10 справочника для 8 класса).
С точки зрения записи условий, конъюнкция аналогична системе с фигурной скобкой.
2.5. Дизъюнкция (логическое сложение высказываний)
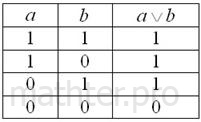
Дизъюнкцией высказываний и называют высказывание (читается «а или бэ»), которое ложно в том и только том случае, когда ложны оба высказывания и :
Предположим, что в экзаменационном билете по высшей математике 2 вопроса и студент сдаёт экзамен, если ответит хотя бы на один вопрос. Рассмотрим следующие высказывания:
– Петя ответил на 1-й вопрос, – Петя ответил на 2-й вопрос.
Дизъюнктивная запись читается просто и понятно: Петя ответил на 1-й или 2-й вопрос и подразумевает три истинных исхода (см. таблицу). При этом экзамен Пётр не сдаст в единственном случае – если «запорет» оба вопроса:
Операция логического сложения также применима для трёх и бОльшего количества высказываний. Некоторые лояльные преподаватели задают 10-15 вопросов и ставят экзамен, если студент хоть что-то знает =)
И, наверное, вы обратили внимание, что логическое ИЛИ отличается от обывательского «или». Люди обычно подразумевают под ним исключающий выбор (или одно или другое). И в математической логике эта операция тоже рассматривается! Она так и называется – Исключающее ИЛИ (англ. XOR). Но возвращаемся к ИЛИ «классическому».
Дизъюнкции соответствует операция объединения множеств. Так, например, запись сообщает нам о том, что «икс» принадлежит интервалу или равен нулю или принадлежит полуинтервалу . Этот же факт можно записать с помощью значка совокупности: . Значок совокупности как раз символизирует связку ИЛИ, но лицезреть его вам придётся намного реже, чем значок системы.
Отрицание, Дизъюнкция и Конъюнкция. Графическое решение логических выражений. Алгебра логики основы
Ну и давайте отвлечёмся от бытового электричества: подавляющее большинство сайтов Интернета расположены на профессиональных серверах, которые снабжаются, как правило, двумя блоками питания. В электротехнике это называется параллельным подключением, которое как раз и моделирует правило ИЛИ – сервер работает, если исправен хотя бы один блок питания. Оборудование, кстати, поддерживает «горячую» замену, т. е. сгоревший БП можно заменить, не выключая сервер. Такая же история с жёсткими дисками – они дублируются в так называемом RAID-массиве, и более того, сам Дата-центр, где находятся серверы, обычно запитывается двумя независимыми электролиниями + дизель-генератор на всякий случай. Эти меры обеспечивают максимальный аптайм сайтов.
И коль скоро речь зашла о компьютерах, то они… базируются на рассмотренных логических операциях! Это кажется невероятным, но задумаемся – а что вообще могут «понимать» эти «железки»? А понимать они могут следующее:
в проводе есть ток – это логическая единица;
провод обесточен – это логический ноль.
И именно данный факт первопричина того, что в основе измерения объёма информации лежит степень двойки:
и т. д.
Простейшим «компьютером» является… обычный выключатель – он хранит информацию в 1 бит (истину или ложь в указанном выше смысле). Центральный же процессор современного компьютера насчитывает сотни миллионов (!) транзисторов, и самое сложное программное обеспечение раскладывается на множество нулей и единиц, которые обрабатываются с помощью элементарных логических операций!
Всё гениальное просто! И уже следующие две операции, которые мы рассмотрим, являются не самостоятельными, то есть могут быть выражены через отрицание, конъюнкцию и дизъюнкцию:
Логическое сложение (дизъюнкция)
Соединение двух (или нескольких) высказываний союзом ИЛИ называется дизъюнкцией или логическим сложением. Логическое сложение схоже с союзом ИЛИ в естественном языке, если он употребляется в смысле «или то, или это, или оба сразу». Операцию логического сложения часто называют операцией ЛОГИЧЕСКОГО ИЛИ .
Высказывание А+В истинно (равно 1) тогда, когда истинно хотя бы одно из входящих в него высказываний А или В, и ложно только тогда, когда ложны оба слагаемых (равны 0).
1 + 1 = 1
Следует обратить внимание на то, что при сложении двух логических единиц получается логическая единица. Алгебра логики оперирует только двумя значениями — ложью (логический 0) и истиной (логическая 1). Истина не может быть двойной или истиной в квадрате, поэтому при сложении двух истин мы получаем просто истину. Точно также при сложении двух логических сигналов высокого уровня мы получаем логический сигнал высокого уровня.
Дизъюнкция обозначается символом v или знаком сложения ( + ).
Правила логического сложения двух высказываний можно свести в следующую таблицу:
| A | B | A + B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Такая таблица называется таблицей истинности для дизъюнкции.
Нетрудно увидеть, что первые три строки таблицы соответствуют правилам сложения двоичных чисел в одном разряде без учета и образования переноса.
Дизъюнкция n переменных ложна тогда и только тогда, когда все составляющие ее переменные ложны.
В логических схемах BEAM-роботов логическое ИЛИ используется для согласования двух логических сигналов.
Другие базовые операции в алгебре логики
Символы и обозначения
Для обозначения дизъюнкции в логике используется символ “∨” (вертикальная черта) или слово “или”.
Например, если у нас есть два утверждения A и B, то их дизъюнкция может быть записана как A ∨ B или A или B.
Также для обозначения дизъюнкции могут использоваться другие символы, такие как “+”, “v” или “∪”. Однако наиболее распространенными и принятыми символами являются “∨” и “или”.
Свойства дизъюнкции
Дизъюнкция – это логическая операция, которая объединяет два утверждения и возвращает истину, если хотя бы одно из утверждений истинно.
Коммутативность
Свойство коммутативности означает, что порядок утверждений в дизъюнкции не имеет значения. То есть, A ∨ B эквивалентно B ∨ A.
Ассоциативность
Свойство ассоциативности означает, что при наличии трех или более утверждений, порядок их объединения в дизъюнкции не имеет значения. То есть, (A ∨ B) ∨ C эквивалентно A ∨ (B ∨ C).
Идемпотентность
Свойство идемпотентности означает, что повторное объединение одного и того же утверждения в дизъюнкции не изменяет ее значение. То есть, A ∨ A эквивалентно A.
Дистрибутивность
Свойство дистрибутивности означает, что дизъюнкция может распространяться на другие логические операции. Например, A ∨ (B ∧ C) эквивалентно (A ∨ B) ∧ (A ∨ C).
Идентичность
Свойство идентичности означает, что если одно из утверждений в дизъюнкции является истиной, то вся дизъюнкция также является истиной. То есть, если A истинно, то A ∨ B также истинно.
Дополнительность
Свойство дополнительности означает, что если одно из утверждений в дизъюнкции является ложью, то вся дизъюнкция зависит от другого утверждения. То есть, если A ложно, то A ∨ B эквивалентно B.
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Связь с естественным языком
В жизни мы постоянно используем слова «или», «либо», «иначе», чтобы объединять несколько своих мыслей в одно высказывание, позволяет выбрать из предложенных вариантов. Так что в естественном языке дизъюнкция также ярко проявляется.
Выражение «Проверим себя или пойдем отдыхать» может быть интерпретировано как дизъюнкция двух высказываний: «Проверим себя», «Пойдем отдыхать». Если ты захочешь проверить себя, короткий тест ждет тебя ниже, если нужна передышка, отдыхай. Но не забудь вернуться к обучению.
В естественном языке принцип дизъюнкции действует так же: если одно из высказываний истинно, то всё выражение будет истинным.

Проверь насколько ты готов к экзамену по информатике

Это займет всего 15 минут, и в конце теста,
тебя будет ждать персональный
образовательный план пройти тест
Проверь себя
В большинстве языков программирования дизъюнкцию обозначают символом:
Есть два высказывания: «Я будущий айтишник», «Этот тест слишком простой». Когда высказывание «Я будущий айтишник или этот тест слишком простой»?
-Когда ложно высказывание «Я будущий айтишник», но истинно «Этот тест слишком простой».
-Когда оба высказывания ложны.
-Я будущий айтишник, этот тест точно слишком простой.
ИМПЛИКАЦИЯ
✑ Сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием (A), а второе (A) является следствием условия (A). .
⚑ Импликацию также называют логическим следованием.
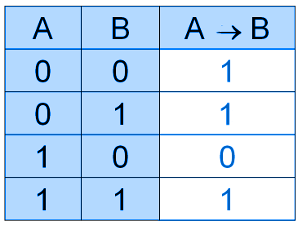
Для записи импликации используют следующие знаки: →, ⇒.
Свойства импликации: A → B = ¬ A ∨ B.
Импликация A→B ложна, если A=1 и B=0. Если A=0, то импликация A→B истинна при любом значении B, (из лжи может следовать истинна).
ЭКВИВАЛЕНТНОСТЬ
✑ сложное логическое выражение, которое истинно на равных значениях переменных A и B .
⚑ Эквивалентность также называют логической равнозначностью.
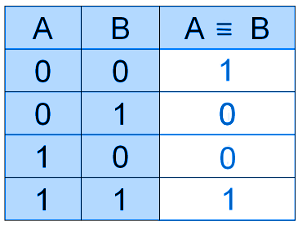
Для записи эквивалентности используют следующие знаки: ↔, ⇔.
Свойства эквивалентности:
- Эквивалентность истинна на равных наборах значений переменных A и B.
- КНФ

- ДНФ