Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики).
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Примеры высказываний:
1. Москва – столица России.
2. Число 27 является простым.
3. Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным, потому что число 27 составное 27 = 3*3*3.
Следующие предложения высказываниями не являются:
- Давай пойдем гулять.
- 2*x > 8.
- a*x2 + b*x + c = 0.
- Который час?
Отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Примеры высказываний:
1. Сегодня светит солнце.
Каждое из этих высказываний характеризует свойства или состояние конкретного объекта (в пермом предложении — погоды, во втором — окружающего мира). Каждое из этих высказываний несет значение «истина» или «ложь».
Простые высказывания назвали логическими переменными, а сложные — логическими функциями. Значения логической функции также только 0 или 1. Для простоты записи высказывания обозначаются латинскими буквами А, В, С.
В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
| Истина | И | True | T |
| Ложь | Л | False | F |
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Логическое выражение — это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции , при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь):
- в естественном языке соответствует союзу «И»;
- в алгебре высказываний обозначение «
- в языках программирования обозначение «And».
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым (или исходным) высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. Если хотя бы одно из составляющих высказываний ложно, то и полученное из них с помощью союза «И» сложное высказывание также считается ложным.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Если два высказывания соединены союзом «И», то полученное сложное высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение, различие):
- в естественном языке соответствует союзу «ИЛИ»;
- в алгебре высказываний обозначение «V» или «+»;
- в языках программирования обозначение «Or».
Дизъюнкция — это логическая операция, которая каждым двум простым (или исходным) высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.
Если два высказывания соединены союзом «ИЛИ», то полученное сложное высказывание истинно когда истинно хотя бы одно из составляющих высказываний.
Рассмотренные выше операции были двуместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко используется и одноместная (унарная) операция отрицание.
Инверсия — отрицание (от латинского disjunctio — разобщение, различие):
- в естественном языке соответствует словам «неверно, что. » и частице «не»;
- в алгебре высказываний обозначение «» или «-»;
- в языках программирования обозначение «Not».
Отрицание — логическая операция, которая с помощью связки «не» каждому исходному высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество, дополняющее его до универсального множества.
Если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным.
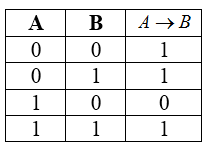
Логическое следование (импликация):
Высказывание, составленное из двух высказываний при помощи связки «если. то. », называется логическим следованием, импликацией (импликация от латинского implico — тесно связываю).
A => B
«Из А следует В»
Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие (посылка А) — истинно, а следствие (заключение В) — ложно и истинно во всех остальных случаях.
Пример. Дано сложное высказывание: «Если выглянет солнце, то станет тепло». Требуется записать его в виде логической формулы. Обозначим через А простое высказывание «выглянет солнце», а через В — «станет тепло». Тогда логической формулой этого сложного высказывания будет импликация: A -> B.
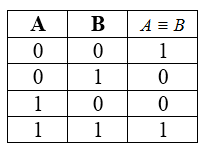
Высказывание, составленное из двух высказываний при помощи связки «тогда и только тогда, когда», называется эквивалентностью (эквивалентность — логическое тождество, равнозначность, взаимная обусловленность.)
A B
«А равносильно В»
Новое высказывание, полученное с использованием эквивалентности, является истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
В алгебре логики логические связки и соответствующие им логические операции имеют специальные названия и обозначаются следующим образом:
| Логическая связка | Название логической операции | Обозначения | ||||||
| не | Отрицание, инверсия | Ø, ù | ||||||
| и, а, но | Конъюнкция, логическое умножение | Быть иль не быть — вот в чем вопрос.» (В. Шекспир) А V A В 2. «Если хочешь быть красивым, поступи в гусары.» (К. Прутков) А => В Построение таблиц истинности и логических функцийЛогическая функция — это функция, в которой переменные принимают только два значения: логическая единица или логический ноль. Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b). Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части — соответствующие значения логической функции. При построении таблицы истинности необходимо учитывать порядок выполнения логических операций. Порядок выполнения логических операций в сложном логическом выражении: Для изменения указанного порядка выполнения операций используются скобки. Алгоритм построения таблиц истинности для сложных выражений: 1. Определить количество строк: количество строк = 2 n + строка для заголовка, n — количество простых высказываний. 2. Определить количество столбцов: количество столбцов = количество переменных + количество логических операций; — определить количество переменных (простых выражений); — определить количество логических операций и последовательность их выполнения. 3. Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности с учетом таблиц истинности основных логических операций. Пример: Составить таблицу истинности логического выражения: D = А — промежуточные результаты (логические операции): А — инверсия (обозначим через E); B Ú C — операция дизъюнкции (обозначим через F); а также искомое окончательное значение арифметического выражения: D = А F — это операция конъюнкции. 3. Заполнить столбцы с учетом таблиц истинности логических операций.
|