Двоичная арифметика Таблица умножения 1 1 0 0 1 0 0 0 х 1001 2 1101 2 1101 1001 х 1 101 0 0 11 1 1 + 1 1 1 1110101 0 1 1 1101 2 х 1001 2 1110101 2 13 10 1001 2 1 2 3 0 2 2 0 2 1 1 2 0 8 1 = 9 10 = 3 2 1 0 1101 2 3 2 1 0
Двоичная арифметика Таблица умножения 1 1 0 0 1 0 0 0 Получив в десятичной системе счисления сомножители, умножим их, т.е. 9 умножаем на 13. Получим число 117. Переведём теперь 117 в двоичную систему счисления. х 1101 1001 х 1 101 0 0 11 1 1 + 1 1 1 111 0 1 1101 2 х 1001 2 1110101 2 = 9 10 117 10 13 10 1001 2 = 3 2 1 0 1101 2 3 2 1 0 13 10 9 10 117 10 1110101 2
Сделайте самостоятельно! Задание 2 Перемножить два двоичных числа 1101 2 и 1001 2 . Перевести исходные числа из двоичной системы счисления в десятичную и перемножить их. Полученное произведение перевести из десятичной системы счисления в двоичную и сравнить результат с ответом, который получился при умножении двоичных чисел.
По теме: методические разработки, презентации и конспекты
Разработка урока на тему: Двоичное кодирование числовой информации. Перевод целых десятичных чисел в двоичный код.
Разработка урока на тему: Двоичное кодирование числовой информации. Перевод целых десятичных чисел в двоичный код.
Двоичная сс. Двоичная арифметика
Разработка ученицы 11 класса.

Урок по информатике в 6 классе по теме «Двоичное кодирование числовой информации. Перевод целых десятичных чисел в двоичную систему счисления»
Урок по информатике в 6 классе по теме «Двоичное кодирование числовой информации. Перевод целых десятичных чисел в двоичную систему счисления»В материалы урока входят конспект урока, презентация.
8 класс ФГОС урок на тему: Двоичная система счисления. Двоичная арифметика
технологическая карта урока.
Двоичные числа. Перевод двоичного числа в десятичное с помощью двоичного ряда, 6 класс
Урок рассматривает вопросы записи чисел в двоичном виде и переводу чисел из двоичной записи в десятичную с помощью двоичного ряда, 6 класс. Презентация, представленная с технологической картой урока, .

Двоичная система счисления. Двоичная арифметика
Методическая разработка к уроку 8 Класс «Двоичная система счисления. Двоичная арифметика
(1) (+) (1) (+) (1) (=) (11).
Рис. (2). Сложение двоичных чисел
Умножим двоичные числа (11011) на (110). Умножение в двоичной системе счисления сводится к многократному сложению.
Рис. (3). Умножение двоичных чисел
Арифметические операции в восьмеричной и шестнадцатеричной системах счисления выполняются аналогичным образом. Нужно построить соответствующие таблицы сложения, вычитания, умножения и деления. Но это весьма трудоёмкий процесс. Вычисления в этих системах счисления лучше доверить компьютеру.
Умножение и деление двоичных чисел
3. Умножение чисел, представленных в форме с фиксированной запятой в дополнительном коде
В случае, когда числа в машине хранятся в дополнительном коде целесообразно все операции над числами производить в дополнительном коде. Однако при этом возникает ряд особенностей, которые необходимо учитывать.
Произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительного множителя, при этом используются модифицированные коды.
Пример 3.2. Умножить числа 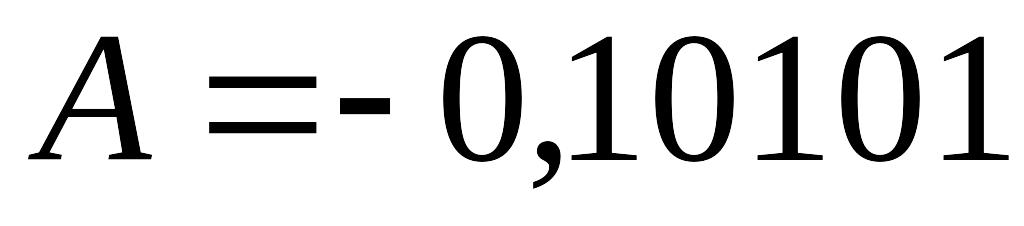 и
и 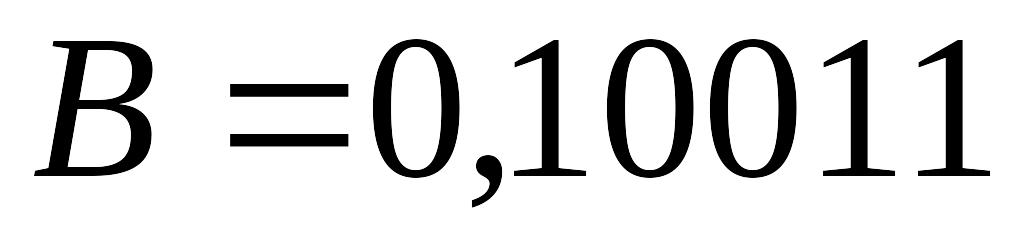 в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
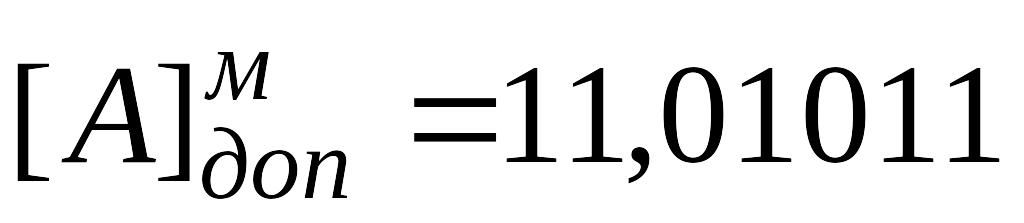
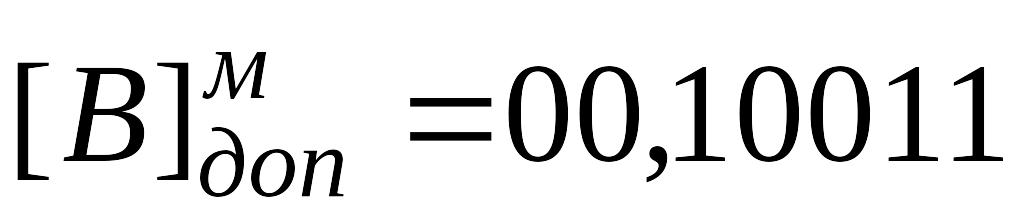
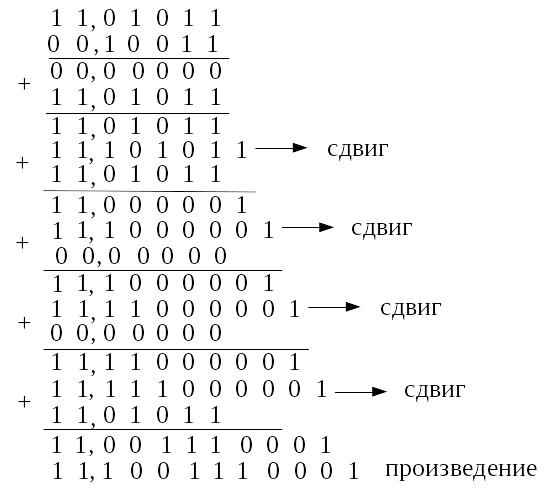
Таким образом 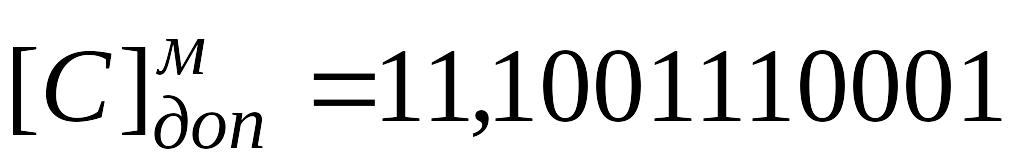 , а
, а 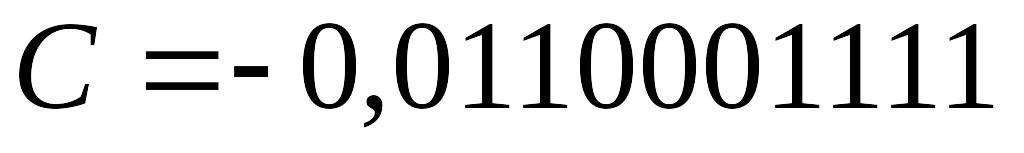 .
.
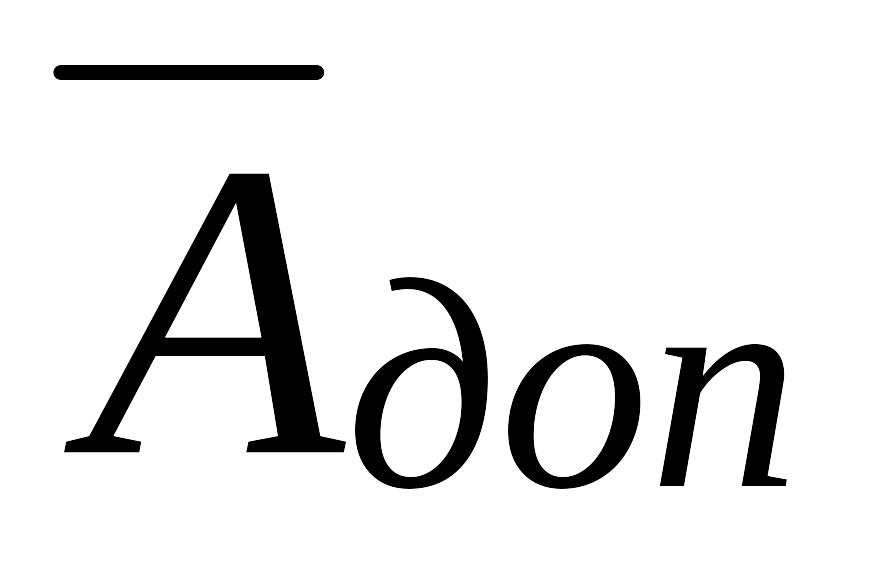
Если множитель отрицательное число, то произведение чисел в дополнительном коде получается прибавлением поправки к произведению дополнительных кодов сомножителей.
Пример 3.3. Умножить числа 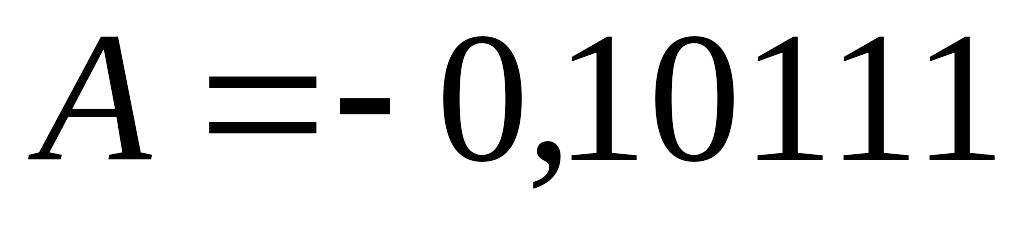 и
и 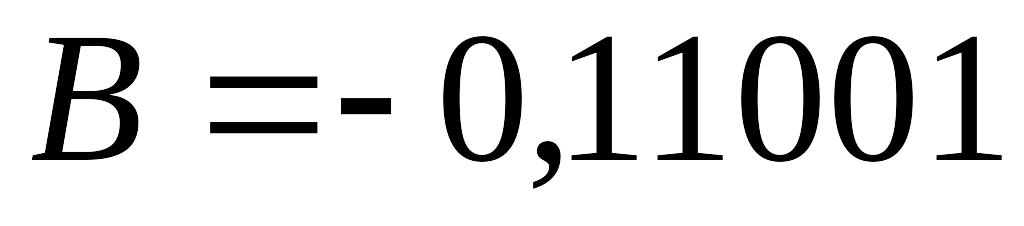 в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
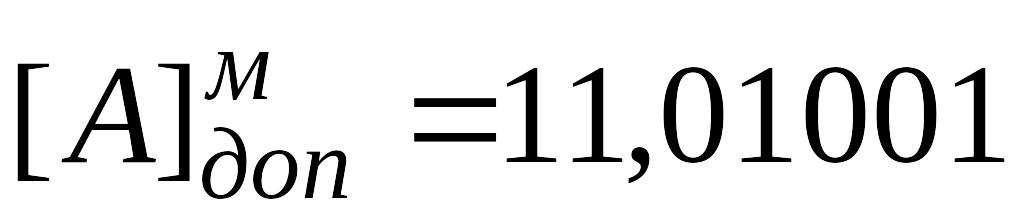
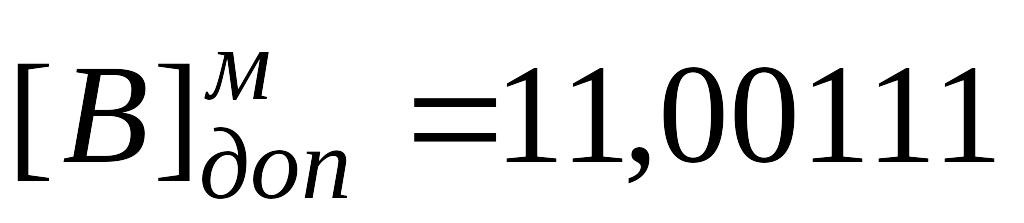
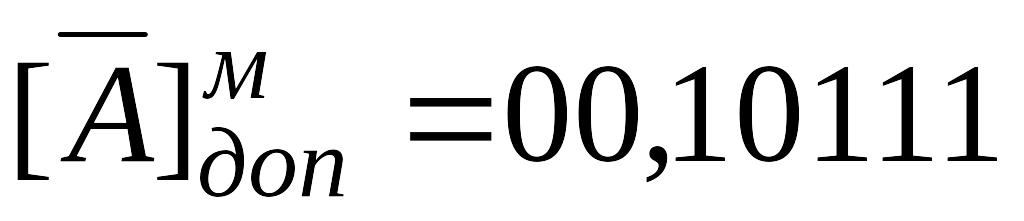
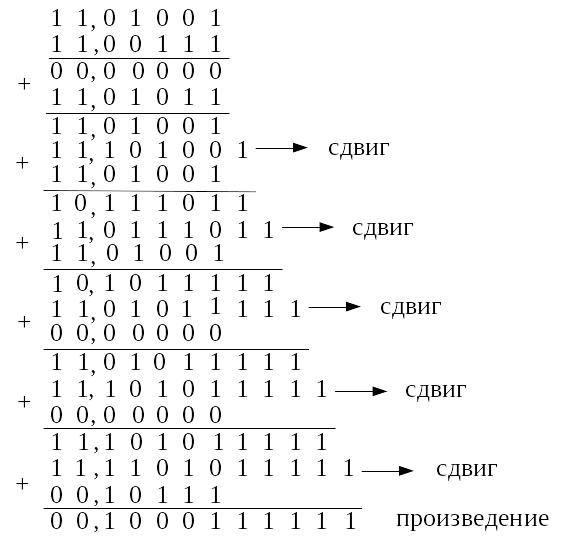
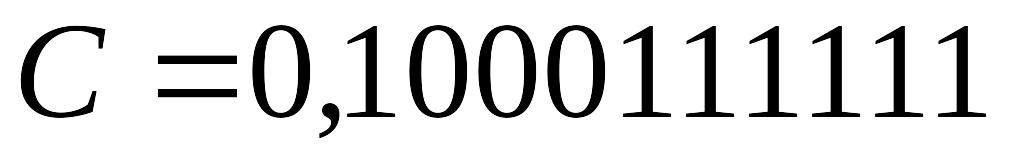
Таким образом .
4. Умножение чисел, представленных в форме с фиксированной запятой в обратном коде
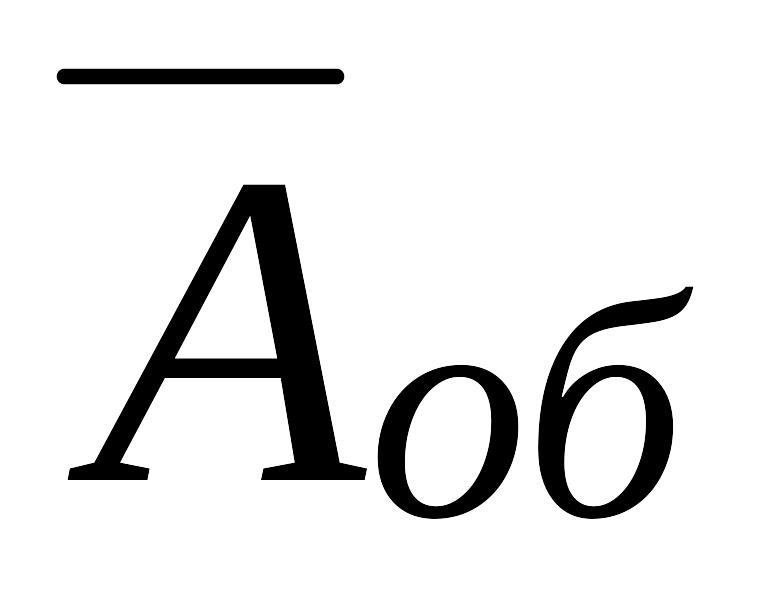
Произведение обратных кодов сомножителей равно обратному коду результата только в случае положительного множителя. Если множитель – отрицательное число, то произведение чисел в обратном коде получается прибавлением к произведению обратных кодов сомножителей.
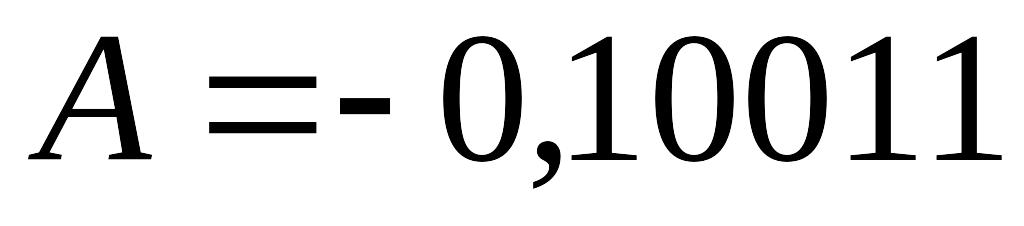
Пример 3.4. Умножить числа и в обратном коде.
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.
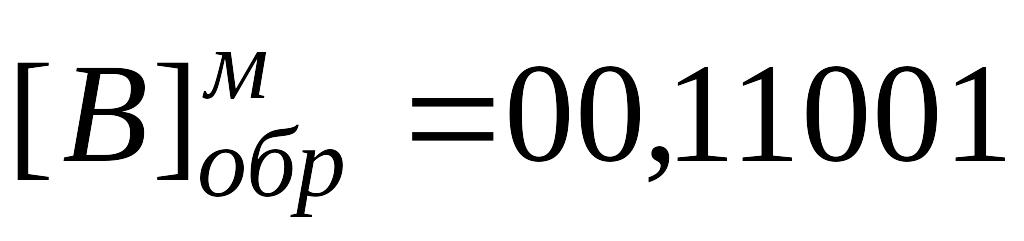
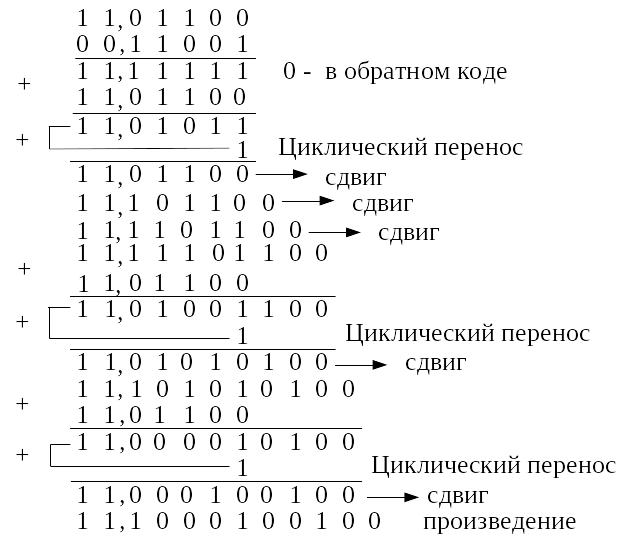
Таким образом, 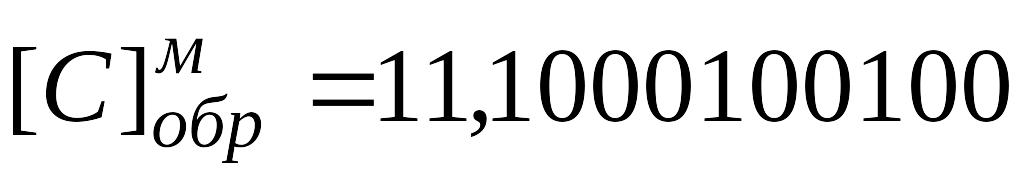 , а
, а 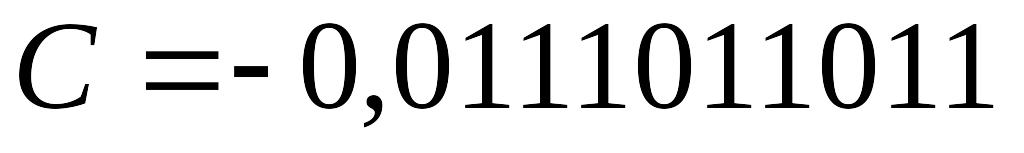
Пример 3.5. Умножить числа и .
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.
Двоичная арифметика
Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.
Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.
При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.
Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.
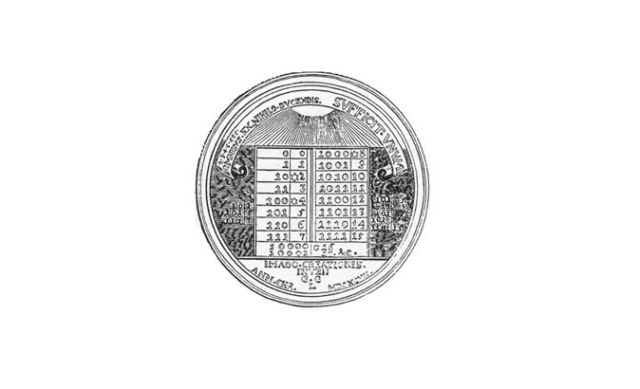
Сложение
Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.
Правила сложения двоичных чисел:
Например, сумма двоичных чисел 1000111 + 110011 = 1111010
Двоичная арифметика
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример : Вычислить 1011,12 + 1010,112

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример : Вычислить 111,12 + 1112 + 101,12

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1. Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Двоичная арифметика
Арифметические действия в двоичной системе производятся по обычным для позиционных систем правилам, которые нам известны из десятичной арифметики, но при этом используются таблицы сложения и умножения двоичной системы:
Таблица сложения

Таблица сложения в двоичной системе очень проста. Надо только помнить, что прибавление нуля не меняет число, а один плюс один, будет два.
Таблица умножения

Таблица умножения ещё проще. Здесь нужно твёрдо знать, что любое число, умноженное на нуль, есть нуль и что умножение на единицу не меняет числа.
Сложение многозначных чисел производится точно так же, как и в десятичной системе, то есть поразрядно, начиная с младшего. Например:

Вычитание в двоичной системе выполняется по таким правилам:


Точки, поставленные над некоторыми разрядами уменьшаемого, показывают, что в двоичной системе единица помеченного разряда раздробляется на две единицы низшего разряда.
Умножение и деление двоичных чисел практически не отличается от умножения и деления чисел, записанных в десятичной системе счисления. Единственным отличием является то, что при умножении в столбик не приходится находить произведение первого множителя на значения последовательных разрядов второго множителя, так как значение этих разрядов 1 или 0. А при делении в столбик не нужно подбирать неполное делимое, так как учитывая специфику двоичных чисел, неполное делимое можно определить просто посмотрев на делимое.
Примеры. Выполнить умножение и деление:
3. Умножение чисел, представленных в форме с фиксированной запятой в дополнительном коде
В случае, когда числа в машине хранятся в дополнительном коде целесообразно все операции над числами производить в дополнительном коде. Однако при этом возникает ряд особенностей, которые необходимо учитывать.
Произведение дополнительных кодов сомножителей равно дополнительному коду результата только в случае положительного множителя, при этом используются модифицированные коды.
Пример 3.2. Умножить числа 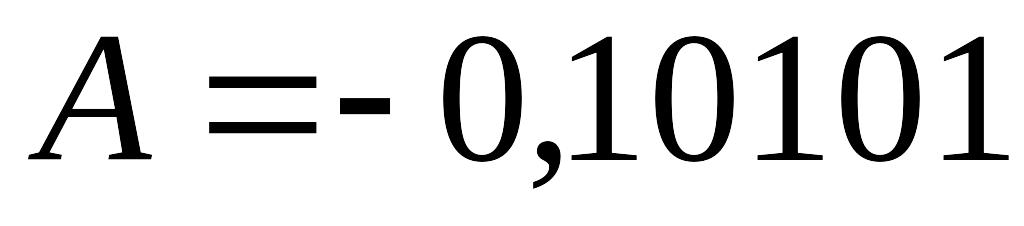 и
и 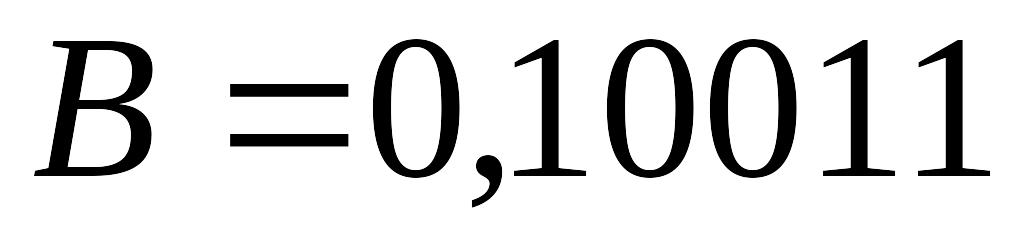 в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
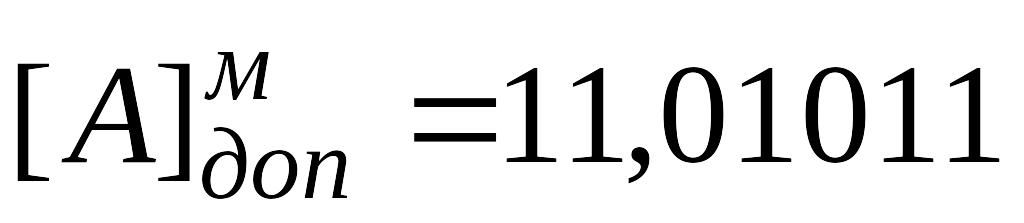
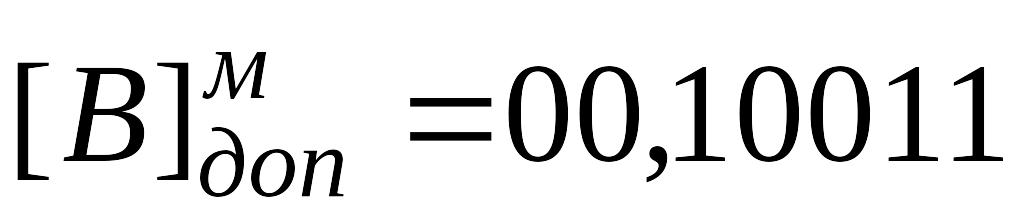

Таким образом 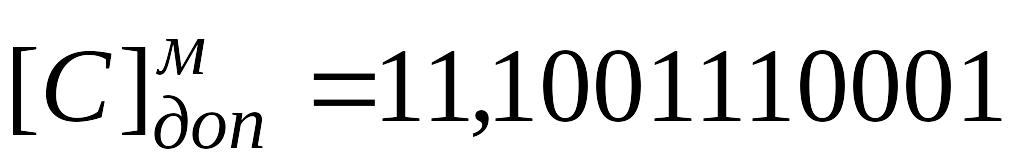 , а
, а 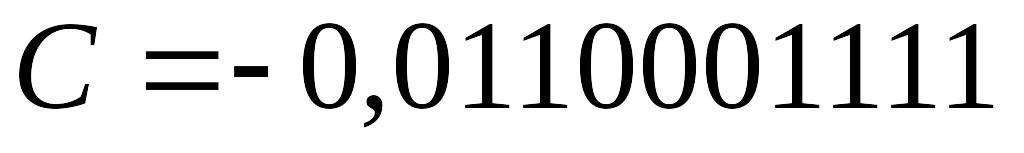 .
.
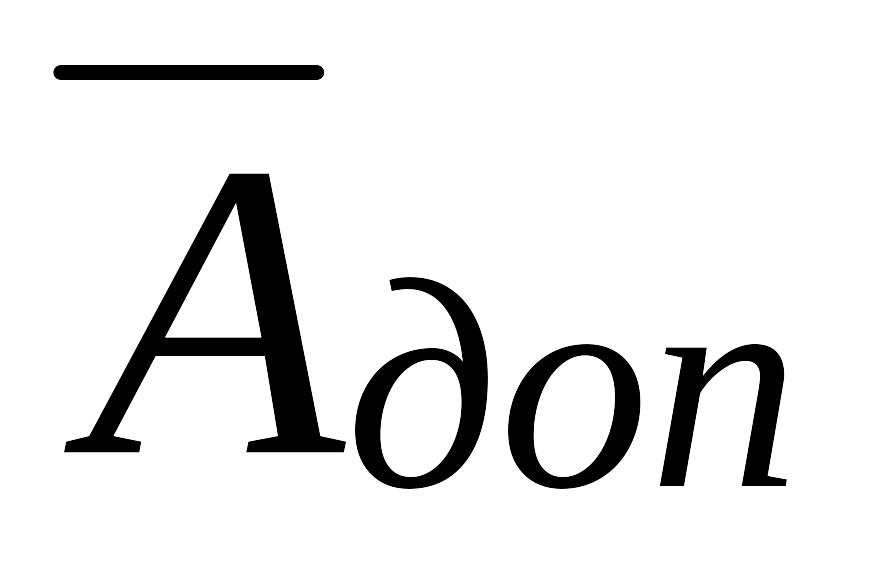
Если множитель отрицательное число, то произведение чисел в дополнительном коде получается прибавлением поправки к произведению дополнительных кодов сомножителей.
Пример 3.3. Умножить числа 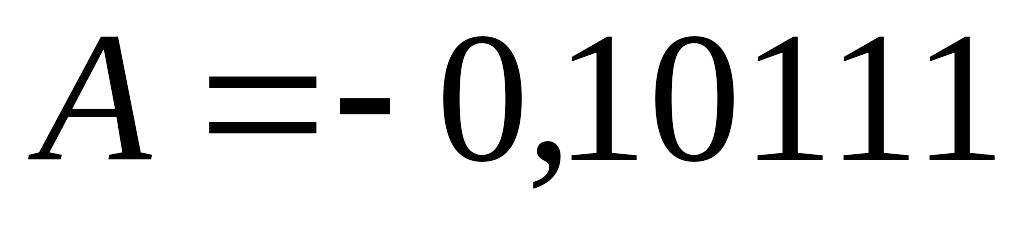 и
и 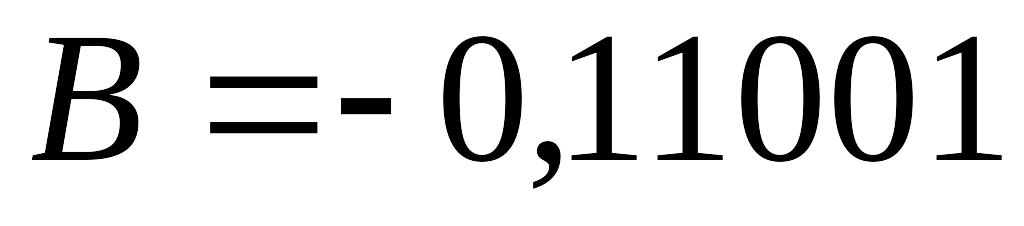 в дополнительных кодах.
в дополнительных кодах.
Решение. Запишем машинные изображения чисел A и B в модифицированном дополнительном коде.
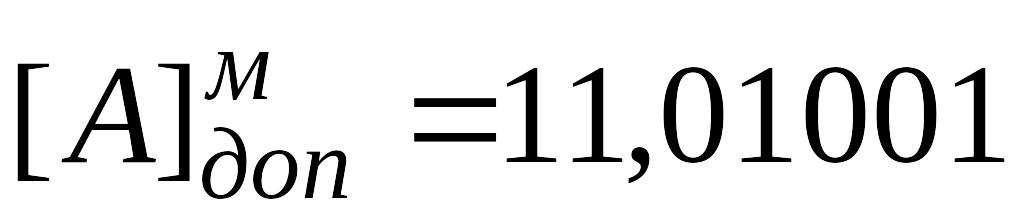
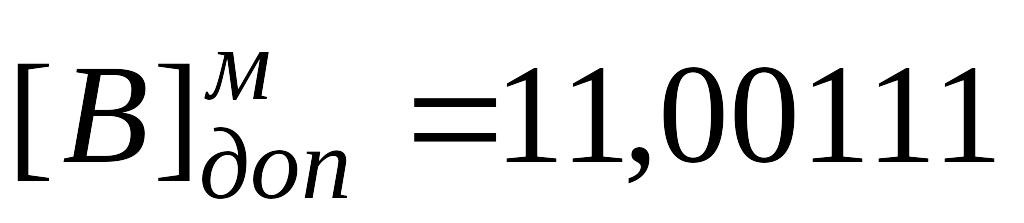
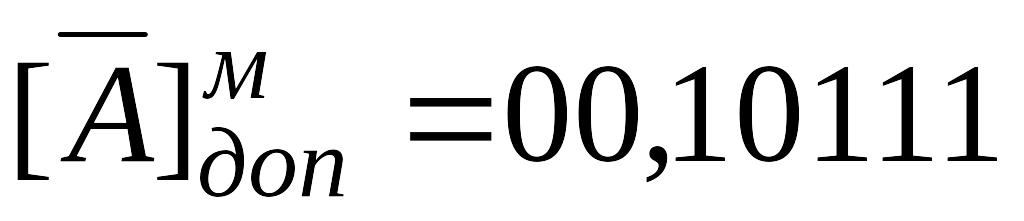

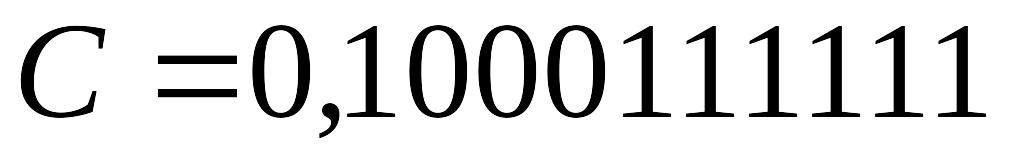
Таким образом .
4. Умножение чисел, представленных в форме с фиксированной запятой в обратном коде
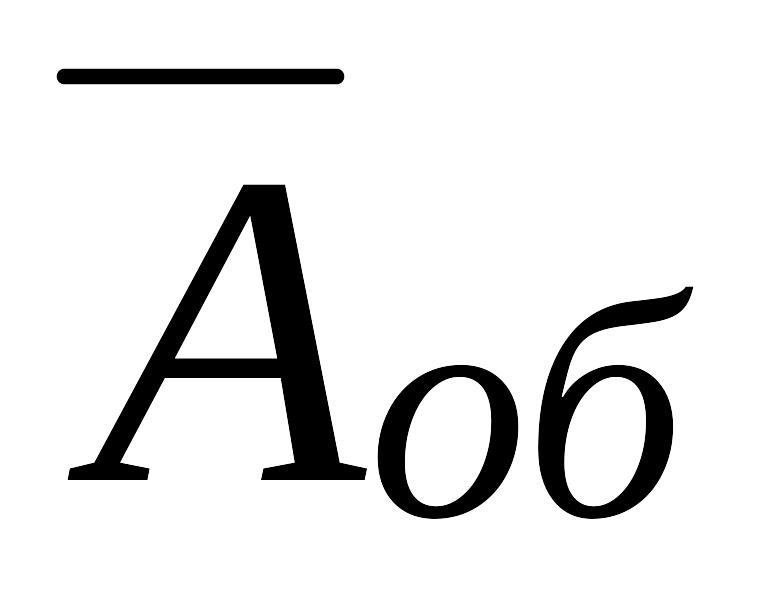
Произведение обратных кодов сомножителей равно обратному коду результата только в случае положительного множителя. Если множитель – отрицательное число, то произведение чисел в обратном коде получается прибавлением к произведению обратных кодов сомножителей.
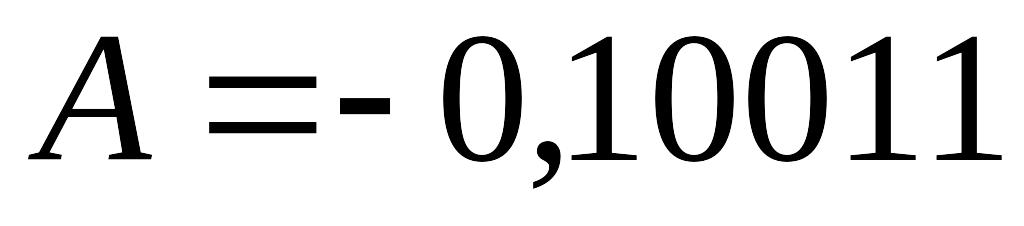
Пример 3.4. Умножить числа и в обратном коде.
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.
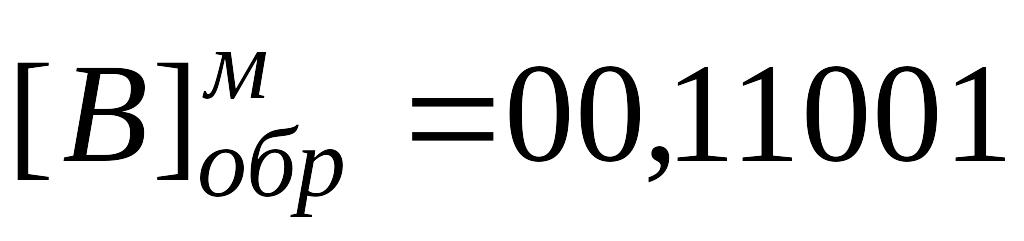

Таким образом, 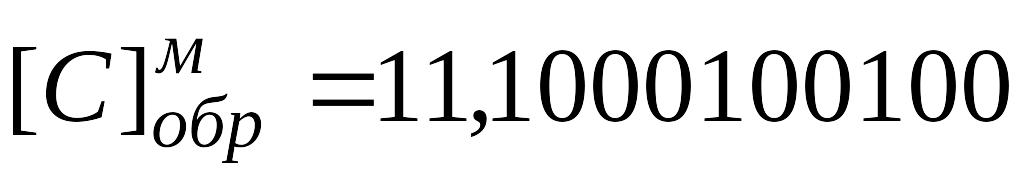 , а
, а 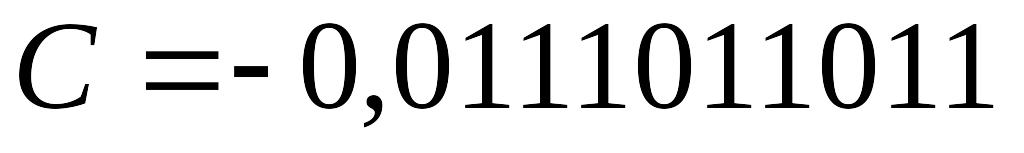
Пример 3.5. Умножить числа и .
Решение. Запишем машинные изображения чисел A и B в модифицированном обратном коде.




