Расчет электрических параметров необходим для правильных построений цепей. Поскольку целью использования электричества в электротехнике является задача по выполнению током работы, то встает вопрос о том, как найти силу тока. Данный параметр используют при вычислениях мощности и в расчетах потребления электрической энергии.
Существуют разные способы определения этого важного параметра, которые мы рассмотрим в данной статье.
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.

Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I 2 R, откуда
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи
показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Что такое внутреннее сопротивление и ЭДС
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.

Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:
Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.
Источник тока

Как мы уже выяснили, электрические схемы не могут работать просто так. Представим, что вы хотите поехать на машине, в которой нет бензина. Конечно, машина не заведется, так как ее нужно заправить. Электрические схемы работают по такому же принципу. Если их не подпитывать током, то они не будут работать.
Электрический ток — это направленное, упорядоченное движение электрических зарядов. Поэтому, чтобы поддерживать в цепи ток длительное время, в нем должен быть участок, на котором будет происходить перенос зарядов против сил электростатического поля (поля, создаваемого неподвижными зарядами). То есть, то место, где электроны будут принудительно приходить в движение.
Источник тока — элемент электрической цепи, в котором на заряды действует сторонняя сила, задающая направление движения зарядов (тока).
Перемещение зарядов на этом участке возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонними силами. Эти силы приводят заряды в движение. Благодаря этому поддерживается ток в цепи. Действие сторонних сил характеризуется величиной, называемой электродвижущей силой источника тока (ЭДС), о которой поговорим чуть позднее.

Примером источника тока может служить обычная батарейка. Вы наверняка замечали, что на пальчиковых батарейках с одной стороны пишется «плюс», а с другой — «минус». Это означает, что электрический ток пойдет от положительной части батарейки к отрицательной. А почему ток выходит из одной части, но заходит в другую?
Для объяснения этого явления рассмотрим картинку ниже. Главным критерием рабочей электрической цепи является ее замкнутость, то есть вся цепь неразрывно связана. Подключим нашу батарейку (источник тока) к электрической цепи, которую также называют внешней электрической цепью.
Как мы видим на этом рисунке, на заряды внутри источника тока действует сторонняя сила ((F_)), от плюса к плюсу) и сила электростатического поля ((F)), которая направлена от плюса к минусу. Без действия сторонних сил внутри источника положительный заряд будет двигаться от «+» к «-» (по направлению силы (F)).
Мы действуем сторонними силами так, чтобы он стал двигаться к «+» (по направлению (F_)), то есть против сил электростатического поля. Тогда заряды вылетают из источника тока и далее по внешней цепи, уже под действием обычного электростатического поля, движутся по стандартным законам от «+» к «-». Это и есть наш долгожданный электрический ток – движущиеся заряды. Если бы мы не действовали сторонними силами, все заряды бы просто сидели на месте («+» окружили бы «-», и наоборот). То есть, сама сторонняя сила задает направление движения заряда.
После того как заряд выходит из источника тока, на него действует только одна сила F. Поэтому он обходит всю цепь и возвращается в этот же источник тока. Там на него вновь действует сторонняя сила, ну а дальше вы уже знаете.
Если бы в источнике тока не было сторонних сил, то все положительные заряды застряли бы у минуса.
Основные параметры источника тока
Как и любой другой элемент электрической цепи, источник тока обладает своими характеристиками, которые могут меняться в зависимости от условий использования. Главными характеристиками являются ЭДС источника тока (электродвижущая сила) и его внутреннее сопротивление.
ЭДС источника тока (ε) — это физический параметр, который характеризует работу сторонних сил ((А_)), затраченную на перемещение зарядов (q) внутри источника.
Внутреннее сопротивление определяет количество потерь энергии при прохождении тока через источник тока.
Стоит понимать, что внутреннее сопротивление появляется из-за неидеальности реальных предметов. Только у идеальных источников тока отсутствует внутреннее сопротивление.

Однако при расчете характеристик электрических схем никакой сложности не возникает, так как мы просто представляем, что в цепи появляется дополнительный резистор (на схемах обозначается прямоугольником и буквой R), сопротивление которого будет равняться внутреннему сопротивлению источника тока.
Раз уж мы затронули расчеты электрических схем, то пора вплотную к ним приблизиться.
Закон Ома для полной цепи
Когда в полной электрической цепи имеется источник ЭДС, в цепи возникает ток. Его величину можно найти, используя закон сохранения энергии и закон Джоуля-Ленца, выражающий энергию, выделяемую на электрическом элементе при прохождении по нему тока.
Если сторонние силы за время $Δt$ переместили заряд $Δq$, то, они совершили работу:
Заряд, переносимый сторонними силами внутри источника, пройдет по цепи за то же время $Δt$, а значит, сила тока в цепи будет равна:
Таким образом, величина работы сторонних сил:
А согласно закону Джоуля-Ленца, ток $I$, прошедший через цепь, создаст некоторое количество теплоты. Во внешней цепи эта теплота выделится на сопротивлении внешней цепи $R$, а внутри источника тока – на его внутреннем сопротивлении $r$:
Вся эта теплота, согласно Закону сохранения энергии, получена в результате работы сторонних сил ($А_ = Q$), то есть:
Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.
Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.
Сложные цепи с несколькими источниками тока
В замкнутой цепи может быть не один источник тока.
В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.
В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.
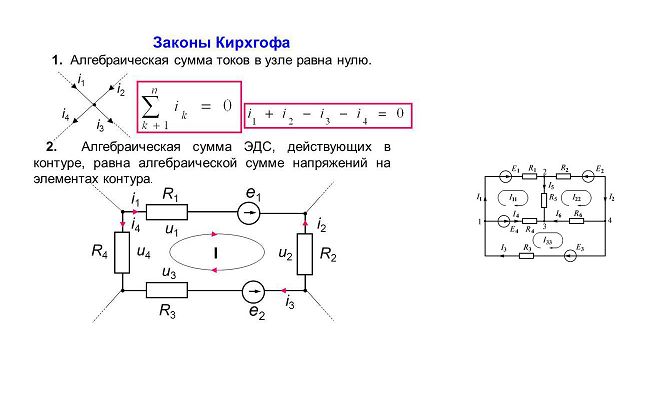
Мнемоническая диаграмма
Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти . Потренируйтесь, это может вам пригодится.
Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.
Закон Ома для полной электрической цепи.
Источник электрического тока, соединенный проводами с различными электроприборами и потребителями электрической энергии, образует электрическую цепь.
Электрическую цепь принято изображать с помощью схем, в которых элементы электрической цепи (сопротивления, источники тока, включатели, лампы, приборы и т. д.) обозначены специальными значками.
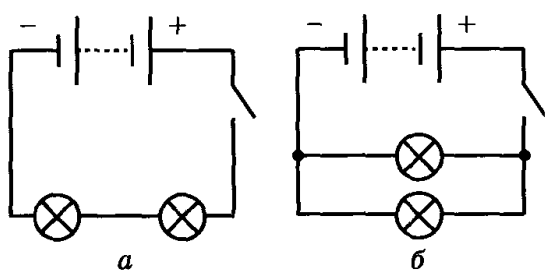
Направление тока в цепи — это направление от положительного полюса источника тока к отрицательному. Это правило было установлено в XIX в. и с тех пор соблюдается. Перемещение реальных зарядов может не совпадать с условным направлением тока. Так, в металлах носителями тока являются отрицательно заряженные электроны, и движутся они от отрицательного полюса к положительному, т. е. в обратном направлении. В электролитах реальное перемещение зарядов может совпадать или быть противоположным направлению тока, в зависимости от того, какие ионы являются носителями заряда — положительные или отрицательные.
Включение элементов в электрическую цепь может быть последовательным или параллельным.
Закон Ома для полной цепи.
Рассмотрим электрическую цепь, состоящую из источника тока и резистора R.
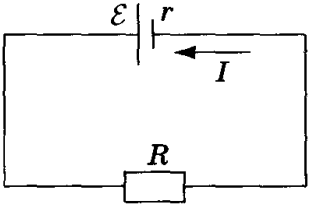
Закон Ома для полной цепи устанавливает связь между силой тока в цепи, ЭДС и полным сопротивлением цепи, состоящим из внешнего сопротивления R и внутреннего сопротивления источника тока r.
Работа сторонних сил Aст источника тока, согласно определению ЭДС (ɛ) равна Aст = ɛq, где q — заряд, перемещенный ЭДС. Согласно определению тока q = It, где t — время, в течение которого переносился заряд. Отсюда имеем:
Тепло, выделяемое при совершении работы в цепи, согласно закону Джоуля — Ленца, равно:
Закон Ома для замкнутой цепи обычно записывается в виде:
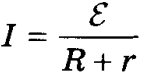
.
Сила тока в полной цепи равна отношению ЭДС цепи к ее полному сопротивлению.
Если цепь содержит несколько последовательно соединенных источников с ЭДС ɛ1, ɛ2, ɛ3 и т. д., то полная ЭДС цепи равна алгебраической сумме ЭДС отдельных источников. Знак ЭДС источника определяется по отношению к направлению обхода контура, который выбирается произвольно, например, на рисунке ниже — против часовой стрелки.
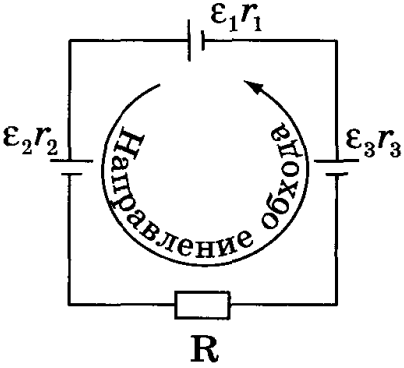
Сторонние силы внутри источника совершают при этом положительную работу. И наоборот, для цепи справедливо следующее уравнение:
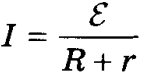
В соответствии с сила тока положительна при положительной ЭДС — направление тока во внешней цепи совпадает с направлением обхода контура. Полное сопротивление цепи с несколькими источниками равно сумме внешнего и внутренних сопротивлений всех источников ЭДС, например, для рисунка выше:
Закон Ома для полной цепи
Когда в полной электрической цепи имеется источник ЭДС, в цепи возникает ток. Его величину можно найти, используя закон сохранения энергии и закон Джоуля-Ленца, выражающий энергию, выделяемую на электрическом элементе при прохождении по нему тока.
Если сторонние силы за время $Δt$ переместили заряд $Δq$, то, они совершили работу:
Заряд, переносимый сторонними силами внутри источника, пройдет по цепи за то же время $Δt$, а значит, сила тока в цепи будет равна:
Таким образом, величина работы сторонних сил:
А согласно закону Джоуля-Ленца, ток $I$, прошедший через цепь, создаст некоторое количество теплоты. Во внешней цепи эта теплота выделится на сопротивлении внешней цепи $R$, а внутри источника тока – на его внутреннем сопротивлении $r$:
Вся эта теплота, согласно Закону сохранения энергии, получена в результате работы сторонних сил ($А_ = Q$), то есть:
Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:
Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.
Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.
Сложные цепи с несколькими источниками тока
В замкнутой цепи может быть не один источник тока.
В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.
В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.

Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Вывод
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.





