Электромагнитная волна характеризуется одним главным параметром — числом гребней, которые за секунду проходят мимо наблюдателя (или поступают в детектор). Эту величину называют частотой излучения ν. Поскольку для всех электромагнитных волн скорость в вакууме (с) одинакова, по частоте легко определить длину волны λ:
Мы просто делим путь, пройденный светом за секунду, на число колебаний за то же время и получаем длину одного колебания. Длина волны — очень важный параметр, поскольку она определяет пограничный масштаб: на расстояниях заметно больше длины волны излучение подчиняется законам геометрической оптики, его можно описывать как распространение лучей. На меньших расстояниях совершенно необходимо учитывать волновую природу света, его способность обтекать препятствия, невозможность точно локализовать положение луча и т. п.
Из этих соображений, в частности, следует, что невозможно получить изображение объектов, если их размер порядка или меньше длины волны излучения, на которой ведется наблюдение. Это, в частности, ставит предел возможностям микроскопов. В видимом свете невозможно рассмотреть объекты размером менее полмикрона; соответственно, увеличение больше чем 1-2 тысячи раз для оптического микроскопа лишено смысла.
Длина стоячей волны
Длиной стоячей волны($lambda_$) называют расстояние в пространстве между двумя пучностями (или узлами):
где $lambda$ – длина бегущей волны. Надо заметить, что расстояние между соседними пучностью и узлом связывает равенство:
Длина бегущей волны
В бегущей волне длина волны связана с фазовой скоростью (vph) формулой:
Разность фаз и длина волны
Две точки волны находящиеся на расстоянии $Delta x$ имеют при колебании разность фаз ($Delta varphi$), которая равна:
Длина волны: определение и расчет
Конечно, у любой волны есть характеристики. Одна из таких характеристик — это длина волны.
- λ — длина волны [м]
Длиной волны называется расстояние между двумя точками этой волны, колеблющимися в одной фазе. Если проще, то это расстояние между двумя «гребнями».
Еще длиной волны можно назвать расстояние, пройденное волной, за один период колебания.
Период — это время, за которое происходит одно колебание. То есть, если дано время распространения волны и количество колебаний, можно рассчитать период.
Формула периода колебания волны
T = t/N
N — количество колебаний [—]
Курсы подготовки к ОГЭ по физике помогут снять стресс перед экзаменом и получить высокий балл.
Выберите идеального репетитора по физике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения

Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Длина волны. Скорость волны | Физика 11 класс #17 | Инфоурок
Формула скорости
= S/t
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
= λ/T
λ — длина волны [м]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
Возьмем формулу скорости:

Математическое представление волн и волновых явлений
Так называемая синусоидальная волна удобна в математическом представлении.
На оси х, как правило, обозначают время распространения волны, а по оси у – положение волны (в том числе, ее амплитуду).
Второй вариант – через использование волновых чисел и угловой частоты. В этом случае показатель длины волны и волновое число будут связаны с частотой и скоростью.
Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь
Мне нужна помощь
Задача 1.
Необходимо найти длину волны, распространяющейся со скоростью 5 метров в секунду. Причем известно, что волна за десять секунд успевает производить 4 полных колебания.
В данном случае можно просто использовать формулу:
Задача 2:
Требуется найти длину колебательной волны, если известно, что дистанция между первой и четвертой стационарными волнами – 15 см.
Длину стоячей волны можно найти по формуле:
С другой стороны:
Здесь Где и n1и n2 являются порядковыми номерами вспученностей.
Согласно условию, n1=1 и n2=4.
Приравняв обе правые части уравнений, можно получить следующее соотношение:
Следовательно, ответом задачи будет — λ=0,1 метра.
Скорость волны в физике
Рисунок 2. Скорость и длина волны. Автор24 — интернет-биржа студенческих работ
Любой волновой процесс распространяется с определенной скоростью. Под быстротой волны считают общий показатель распространения противодействия. Например, удар по торцу металлического стержня образует в нем местное прочное сжатие, которое затем будет двигаться вдоль выколотки со скоростью примерно 10 км/с.
Скорость волны можно определить свойствами окружающей среды, в которой этот процесс происходит. При трансформации волны из одного пространства в другое ее скорость кардинально изменяется.
В физике под длиной волны подразумевают расстояние, на которое может распространиться волна за время, равное общему периоду колебаний в ней.
Определение 3
Скорость волны — это абсолютная и постоянная величина для определенной среды, равная произведению скорости на время ее генерализации.
Таким образом, чтобы измерить длину волны, надо скорость волнового процесса умножить на фазу его колебаний в ней: где $v$ — скорость конкретной волны, $T$ — период общих колебаний в волне, $lambda$ — длина самой волны.
Указанная формула определяет связь длины волны с ее скоростью и фазой. Учитывая, что промежуток колебаний в волновых процессах всегда пропорционален частоте, можно утверждать, что что скорость волны равна созданию длины на стабильную частоту колебаний в ней.
Замечание 1
Волны способны передавать силу и энергию, а также обладают конкретикой, что способствует одному волновому процессу не влиять на колебания другого.
В результате, эти две гранитизации могут легко проходить параллельно и не мешать друг другу.
Виды волн
Волны с точки зрения физики передают общую звуковую энергию, которая легко может существовать в любой среде. Благодаря разнообразию существующих волновых процессов, их невозможно точно определить и выделить основные характеристики, присущи только этому явлению.
Волновой процесс имеет многогранную природу в физике, сюда относят:
- химическую;
- механическую;
- электромагнитную;
- спиновую волны;
- гравитационную;
- плотность вероятности.
Американские ученые два года назад получили Нобелевскую премию за изобретение уникального детектора, которые способен с точностью измерить указанные показатели. Устройство в лазерной гравитационно-волновой обсерватории в первый раз зафиксировало гравитационную волну. Чтобы указанный вид волн долететь до нашей планеты, ему понадобилось более одного миллиарда лет. Далеко за видимым горизонтом галактики произошло мощное столкновение двух черных дыр, после чего прошло уже полтора миллиарда лет.
Звуковыми волнами принято считать волны, которые легко воспринимаются человеческим ухом. Диапазон этих частот находятся в границах примерно от 20 Гц до 20 кГц, а волновые процессы с частотой менее указанных показателей называются инфразвуком, а с частотой более 20 кГц – ультразвуком. Волны звукового диапазона могут находится не только в газе, но и в жидкости, и в других состояниях. Однако волны в газообразном пространстве – среде нашего обитания – представляют собой особый интерес.
Волна и ее распространение
Движение – форма существования материи. Одним из широко распространенных в природе движений является колебательное движение, при котором измеряемая величина изменяется не монотонно, а циклически увеличивая и уменьшая свое значение.

В протяженных объектах любые изменения (и в том числе колебательные процессы), как правило, происходят не сразу во всем объекте, а сперва начинаются в одной его части, а потом распространяются на остальной объект.
Для наблюдения распространения колебательных движений удобно использовать поверхность воды. В первый момент колеблются только частицы воды непосредственно в месте возникновения волны. Далее происходит распространение колебательного движения. При этом сами частицы воды в горизонтальном направлении не движутся, движется лишь само колебание водной глади.

Волна – это колебания среды, распространяющиеся в ней с течением времени.
Параметры волны
Фаза, период и частота
Для распространяющейся волны можно ввести параметр, который называется фазой. Фаза – это одинаковое состояние среды распространения. Для поверхности воды фаза – это величина отклонения от спокойного состояния (от нулевого уровня). Точки волны, находящиеся в одинаковом состоянии, будут находиться в одинаковых фазах. Если записывать в таблицу время, проходящее между одинаковыми фазами какой-то точки, то можно заметить, что это время будет кратно некоторому минимальному значению. Это значение, минимальное время, за которое волна оказывается в одной и той же фазе, называется периодом колебаний $T$ волны. Число периодов за одну секунду называется частотой волны $nu$ (для обозначения используется греческая буква «ню»):
Фазу можно сопоставить с углом на координатной плоскости. Полная волна соответствует углу $2pi$, все фазы повторяются с этим периодом точно так же, как повторяется значение круговых функций (синуса, косинуса и других).
Одному значению отклонения от нулевого значения соответствуют две фазы – одна в момент возрастания, другая – в момент спадания волны (исключение – самый «пик» или самое «дно» волны). Это разные фазы, путать их не следует.
Скорость распространения и длина волны
Поскольку волна распространяется не мгновенно, то, отметив одинаковую фазу волны (движущийся гребень), можно определить скорость этого распространения $v$ относительно неподвижных предметов (например, относительно берега, в случае, когда волна распространяется вдоль него). Для вычисления используется обычная формула скорости – отношение пройденного расстояния к прошедшему времени. Кроме того, можно ввести понятие «длина волны».
Расстояние, которое проходит волна за один период колебания, называется длиной волны, для обозначения используется греческая буква $lambda$ (лямбда). Формула длины волны:
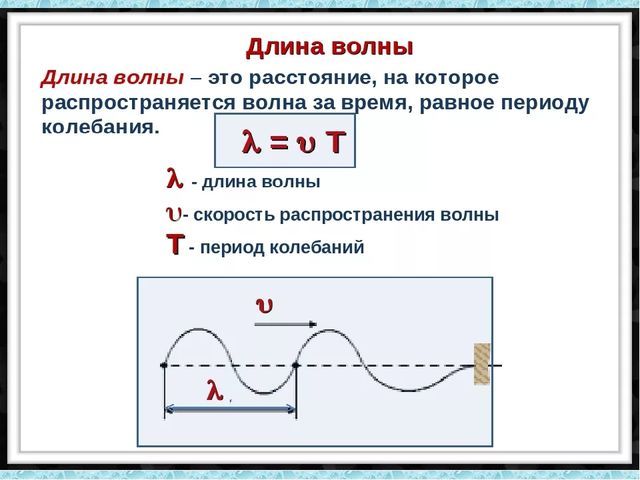
Если известна частота колебаний, для расчета удобнее пользоваться другой формулой (она вытекает из определения частоты):
Слышимый звук представляет из себя колебания плотности воздуха. Распространяется он в нормальных условиях со скоростью, имеющей значения порядка 300-350м/с, и имеет длину волны от ~15мм (самые высокие частоты) до ~15м (самые низкие частоты)
Скорость и длина волны
Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:
где
v — скорость волны; T — период колебаний в волне; λ (греческая буква «ламбда») — длина волны.
Выбрав направление распространения волны за направление оси x и обозначив через y координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45. Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны λ.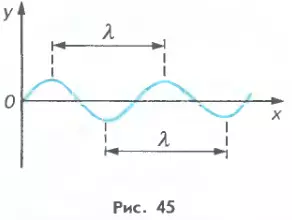
Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т. е. T = 1/ν, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой: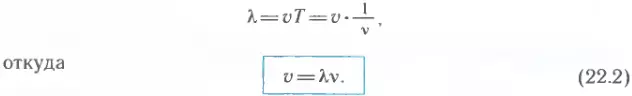
Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
1. Что понимают под скоростью волны? 2. Что такое длина волны? 3. Как длина волны связана со скоростью и периодом колебаний в волне? 4. Как длина волны связана со скоростью и частотой колебаний в волне? 5. Какие из следующих характеристик волны изменяются при переходе волны из одной среды в другую: а) частота; б) период; в) скорость; г) длина волны?
Экспериментальное задание. Налейте воду в ванну и посредством ритмичных касаний воды пальцем (или линейкой) создайте на ее поверхности волны. Используя разную частоту колебаний (например, касаясь воды один и два раза в секунду), обратите внимание на расстояние между соседними гребнями волн. При какой частоте колебаний длина волны больше?




