Что такое скважность импульса

Содержание

Электрические сигналы, амплитуда которых имеет только 2 допустимых состояния: низкого уровня – «0» или высокого уровня – «1», называются импульсными. Одним из важных параметров периодического импульсного процесса является скважность импульсов.

Скважность (S) – это безразмерная величина, характеризующая некоторые свойства периодического импульсного сигнала.
Рассчитывается значение скважности – как отношение его периода повторений (Т) к длительности импульса (tи).
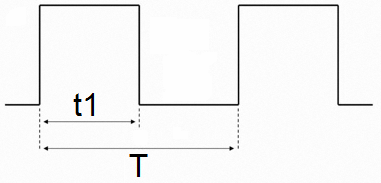
Длительностью импульсного сигнала считается временной интервал высокого (по отношению к показателю основания импульса) уровня напряжения (Рис.1).

Поскольку длительность импульса не может превышать его период, то, как следует из определения, значение скважности всегда должно быть больше единицы!

Если длительность импульса равна половине периода, то скважность равна двум, а сам такой сигнал является симметричным и называется меандром.

Рис.1 Форма импульсного сигнала и примеры импульсов разной скважности

Иногда в радиотехнике используется величина, обратная скважности, называемая коэффициентом заполнения (D).
Таким образом, для импульсного сигнала справедливы следующие простейшие соотношения:
S = T/tимп ;
D = 1/S = tимп/T ;
T = tимп + tпаузы ;
F = 1/T ,
где S – это скважность импульсов, D – коэффициент заполнения, Т – период, tимп – длительность высокого (положительного) уровня импульса, tпаузы – длительность низкого (отрицательного) уровня.

Сдобрим пройденный материал парой незамысловатых онлайн калькуляторов.

Онлайн расчёт длительности импульса по частоте и скважности

А теперь для тех, кто измерил длительности импульсов – всё то же самое, только наоборот:

Онлайн расчёт скважности по длительности импульса

Что такое скважность импульсов и как её определить?

Онлайн калькуляторы перевода длительности импульсов в скваж- ность и скважности в длительность

Скважность

Рис.1 Форма импульсного сигнала и примеры импульсов разной скважности

Сдобрим пройденный материал парой незамысловатых онлайн калькуляторов.

Онлайн расчёт длительности импульса по частоте и скважности

А теперь для тех, кто измерил длительности импульсов – всё то же самое, только наоборот:

Онлайн расчёт скважности по длительности импульса

Что такое скважность

Одной из важнейших величин в импульсной технике является скважность S. Скважность S характеризует прямоугольный импульс, и определяет то, во сколько раз период импульса T больше его длительности t1. Так, меандр, например, имеет скважность равную 2, поскольку длительность импульса в такой последовательности равна половине его периода: S=T/t1=2.

Как видим, и в числителе, и в знаменателе стоят продолжительности, измеряемые в секундах, поэтому скважность — величина безразмерная. Для справки напомним, что меандр — это такая импульсная последовательность, где длительность положительной части импульса t1 равна длительности его исходного состояния t0.

Величина обратная скважности называется коэффициентом заполнения D. Таким образом, теоретически скважность может изменяться от бесконечности до 1, тогда как соответствующий ей коэффициент заполнения может принимать значения от 0 до 1. Записывать величину скважности часто более удобно, чем коэффициент заполнения в виде дроби.

Например: D=0.5 – коэффициент заполнения меандра, или скважность S=2 – более удобочитаемая запись того же самого. Скважность S=10 соответствует коэффициенту заполнения D=0.1 — имеется ввиду, что продолжительность импульса в 10 раз меньше его периода (суммы его положительной и исходной частей).

Когда заходит речь о широтно-импульсной модуляции (ШИМ), то говорят, что при в драйвере происходит изменение ширины или длительности импульса, практически имеется ввиду изменение скважности при постоянной частоте. В этом контексте чем больше скважность — тем уже импульс, чем меньше скважность — тем шире импульс.

Здесь и просматривается этимологическая связь с русским словом «скважина»: большая скважина (по сути — яма между импульсами в последовательности) — сам импульс выглядит как более узкий, маленькая скважина — импульсы широкие (а вот яма между ними — узкая).

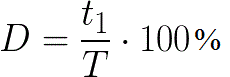
В англоязычной литературе не используется термин «скважность», а используется лишь термин «duty cycle» — рабочий цикл, являющийся аналогом русскоязычного термина «коэффициент заполнения» (D), только указывается он обычно не дробью, а в процентах. Например, мы пишем D=0.5, а в англоязычной литературе можно встретить 50% duty cycle или D = 50%, когда речь идет о меандре. Или D = 30% если длительность импульса соотносится с его периодом как 30 к 100.

Давайте рассмотрим простой практический пример. Лампочка включается на одну секунду через каждые 59 секунд, затем на 59 секунд гаснет, и так все время повторяется в течение неопределенного времени.

Что это значит? Длительность импульса t1 = 1 секунда, период импульса T = 59+1 = 60 секунд. Следовательно с какой скважностью включается лампочка?

Со скважностью S = 60/1. Скважность 60. Значит коэффициент заполнения равен 1/60, то есть D = 0,01666 или duty cycle 1,66%. В данном примере отчетливо видно, что запись в терминах скважности S = 60 более удобочитаема и точна, чем запись в форме коэффициента заполнения D = 0,01666 или duty cycle 1,666%.

Наконец, еще одно полезное применение скважности. Счетчики-дешифраторы импульсов (типа К561ИЕ8) способны делить импульсную последовательность на отдельные импульсы, здесь снова значение скважности подходит лучше, оно может быть определено через разрядность счетчика и сосчитано (пропорционально количеству импульсов, подсчитанных счетчиком).

Таким образом, даже для цифровой техники оперирование напрямую скважностью импульсов часто оказывается более удобным, чем свойственным принятому в англоязычной литературе коэффициентом заполнения.

Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика

Формирование импульсов с заданной скважностью

Для формирования электрических импульсов с определенными параметрами, в том числе скважностью, используются специальные схемы.

С помощью RC-цепочки и компаратора
С использованием мультивибратора
На основе микроконтроллера или микросхемы ШИМ-контроллера

Наиболее точное и гибкое управление параметрами импульсов обеспечивает применение микроконтроллеров и микросхем.

Одним из популярных решений является микросхема таймера NE555. С ее помощью можно формировать импульсы с регулируемой скважностью от 50% до 100%. Другим вариантом могут быть микроконтроллеры серии AVR или микросхемы управления мощностью на основе ШИМ.

Принцип ШИМ (широтно-импульсной модуляции) как раз и основан на изменении скважности импульсов для регулирования различных параметров в электронных схемах.

Конкретный метод формирования выбирается исходя из требований к параметрам импульсов и особенностей применения.

Измерение скважности импульсов

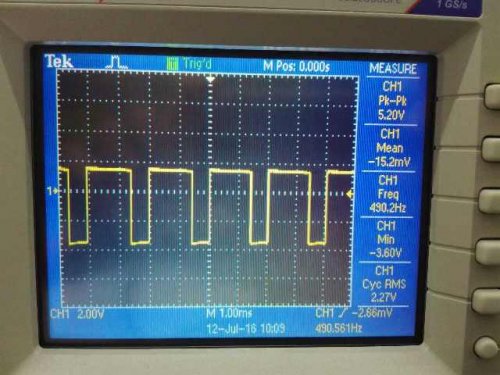
Для анализа и контроля параметров импульсных сигналов необходимо уметь точно измерять скважность импульсов. Для этого применяют такие приборы, как осциллограф, частотомер и цифровой мультиметр.

На экране осциллографа наглядно видны длительности импульсов и пауз. По полученной осциллограмме можно определить t1, T и рассчитать скважность.

Ликбез КО. Лекция №3 Что такое скважность.

Если длина импульса равна половине периода, то скважность равна двум, такой сигнал называется меандром. Длительность такого импульса и .

11 июля 2013, четверг 06:38

OQtagooi [ ] для раздела Блоги

Что такое скважность.
Скважностью называют безразмерную физическую величину, характеризующую любую импульсную систему. Она обозначается буквой S и определяется отношением периода импульсных сигналов T к их длительности. Кроме того существует так же величина обратная скважности, ее называют коэффициентом заполнения и обозначают буквой D, а по-английски она называется Duty cycle.

Если длина импульса равна половине периода, то скважность равна двум, такой сигнал называется меандром. Длительность такого импульса и паузы между имульсами в периоде равны. Скважность может выражаться в процентах и является важной характеристикой импульсной системы, поскольку определяет отношение пиковой мощности импульсной установки к ее средней мощности. Недостаточно высокая скважность систем дискретной обработки информации приводит к ее искажению.

other_material_inline_bottom

Лента материалов

other_material_bottom

Правила размещения комментариев

Соблюдение Правил конференции строго обязательно!
Флуд, флейм и оффтоп преследуются по всей строгости закона!

Комментарии, содержащие оскорбления, нецензурные выражения (в т.ч. замаскированный мат), экстремистские высказывания, рекламу и спам , удаляются независимо от содержимого, а к их авторам могут применяться меры вплоть до запрета написания комментариев и, в случае написания комментария через социальные сети, жалобы в администрацию данной сети.

Что такое ШИМ

Что такое электрический импульс? Это резкий конечный всплеск напряжения в системе. Поскольку он конечен, то он имеет начало, обычно называемое фронтом, ширину и спад, его окончание, период.

Такие всплески можно охарактеризовать следующими параметрами:

периодичность – это временной период до фронта следующего импульса, обозначается литерой T;
скважность – отношение периода к ширине, это величина безразмерная и выражается чаще всего в процентах, на схеме можно обозначить участок между спадом первого импульса и фронтом нового, обозначается литерой S;
частота сигнала – количество всплесков за определённый промежуток времени, величина, обратная периоду колебаний;
ширина импульса – период времени, в течение которого его амплитуда стабильна;
коэффициент заполнения – значение, обратное скважности, обычно обозначается в формулах литерой t.

Таким образом, скважность импульса – это соотношение:

Благодаря этому, широтно-импульсная модуляция позволяет управляемо изменять напряжение в системе от нулевого значения до максимальной амплитуды сигнала, это используется для установки оптимальных режимов работы инерциальных систем.

Применение

Для формирования прямоугольных колебаний применяется микросхема аналогового типа или чип-контроллер. Сами колебания управляют только нагрузкой, идущей от источника тока. Подключение производится через ключевую схему на полупроводнике. Ключ имеет всего два состояния: либо он включён в сеть, либо размыкает её.

Грубо говоря, все зависит от характеристик колебаний. Так, если светильник подключен через подобную схему, то при низкой частоте работы устройства лампа будет мигать с определенной периодичностью, но при превышении её сверх 50Гц в человеческих глазах отдельные всплески света сольются в одно ровное свечение. Это особенность человеческого глаза, который не улавливает колебания свыше этого значения. Но и яркость свечения можно регулировать. Чем ниже коэффициент заполнения, а, следовательно, и значение, обратное ему, тем меньше яркость свечения источника.

Аналогичный пример можно использовать и с двигателем постоянного тока, под управлением широтно-импульсного регулятора. При этом низкая частота приведёт к снижению оборотов двигателя, в то время как высокая – к его эффективной работе. Для её достижения используются ключи-полупроводники, обладающие значительным быстродействием и низким коэффициентом проводимости, так как в противном случае возможно запаздывание сигнала.

При необходимости сигналы схемы импульсного регулятора можно усреднять, для этого используются фильтры низких частот, но при подключении двигателя с большой механической инерцией и хорошим значением индуктивности. В этом случае снижение амплитуды и частоты происходит самопроизвольно.

Скважность, а также её обратное значение зависят от уровня моделирующего сигнала, частота таких устройств определяется частотой дублирующего генератора, подающего дополнительный сигнал.

Генератор для получения скважности

Скважность – одна из характеристик импульсного сигнала

Амплитуду (размах колебаний), обозначаемую как Um.
Их полную длительность – t1.
Продолжительность паузы – tn.

Одна из важнейших характеристик последовательности из повторяющихся во времени сигналов – период их следования T. Иногда этот показатель выражается в виде обратной величины, называемой частотой f = 1/T.

Понятие «скважность» применимо только для периодически повторяющихся импульсных сигналов (для одиночного импульса с передним и задним срезами определиться с ее значением невозможно). Эта величина указывает на то, насколько период последовательности импульсов (T) больше длительности каждого из них (t1). В качестве примера чаще всего рассматривается меандр, скважность S которого соответствует двум единицам (средняя последовательность импульсов на Рис.-1).

Это означает, что длительность импульса в меандре вдвое меньше, чем его период: S=T/t1=2. Из соотношения видно, что размерность обеих сравниваемых величин – продолжительность по времени, измеряемая в секундах. Из этого следует, что сама скважность – безразмерная величина. Период типового импульсного сигнала в любом случае больше его длительности, из чего следует, что значения этого показателя никогда не достигают единицы.

Разновидности импульсов, у которых учитывается скважность

В современных цифровых устройствах действуют импульсы самой различной формы, зависящей от того, как изменяется их величина во времени. На практике чаще всего встречаются импульсные сигналы следующего вида (Рис.-2):

Прямоугольные.
Их трапецеидальные аналоги.
Ступенчатые, пилообразные и треугольные.
Экспоненциальные импульсы.
Колокольчатые сигналы.

Технические показатели, имеющие отношение к форме импульсов, в основном касаются свойств отдельных участков их графического представления. Идеальный прямоугольный сигнал – это формальное изображение периодического колебания более сложной формы. В действительности из-за наличия паразитных связей и переходных процессов форма реального импульса существенно отличается от прямоугольного вида (Рис.-3).

Основные параметры таких сигналов, это:

Размах или амплитуда импульса – Um.
Его длительность – tи.
Длина переднего среза (фронта) – tф.
Длительность заднего среза – tсп.

К этим показателям при необходимости добавляются спад вершины сигнала, а также размах и длительность выброса заднего фронта. При определении скважности последовательности импульсов обязательно учитывается уровень, на котором измеряется этот показатель. В импульсной технике за ориентир берется его величина в пределах от 0,1 до 0,9 от амплитуды сигнала в Вольтах.

Для визуальной оценки реальной формы исследуемых импульсов удобнее всего воспользоваться осциллографом, на экране которого формируются их изображения. Частота следования импульсов определяется с помощью частотомера.

Что такое коэффициент заполнения и чем он неудобен при расчетах

Величину, обратную скважности специалисты называют коэффициентом заполнения и обозначают его как D. В теоретических расчетах скважность может изменяться от бесконечного значения до единицы (не включительно). При этом соответствующий ей коэффициент заполнения D варьируется в диапазоне от нуля до значений, близких к единице.

На практике чаще пользуются показателем скважности, поскольку записывать коэффициент заполнения в виде десятичной дроби не совсем удобно. Так вместо записи D=0,5 (для меандра) его скважность представляется в более удобной форме S=2. Еще один пример удобства пользования этим коэффициентом – проектирование распространенных в электронике счетчиков и дешифраторов импульсов различной длительности.

Эти элементы цифровой техники при включении в схему выполняют функцию делителей частоты, так что в этом случае коэффициент пересчета имеет большое значение. При подсчете импульсов скважность очень удобна тем, что по ее значению легко определяется нужная разрядность электронных счетчиков. В отличие от зарубежной практики, где чаще пользуются обратным показателем, у нас в стране предпочтение отдается именно ей.

Удобство представления скважности на бытовом примере

Убедиться в целесообразности использования при расчетах скважности вместо коэффициента заполнения позволяет следующий бытовой пример. Воспользуемся лампочкой накаливания, которую будем включать через каждые 29 секунд на одну секунду.

В этом случае череда включений и выключений лампочки может быть представлена в виде последовательности импульсов с односекундной длительностью. Период этого повторяющегося процесса складывается из времени, когда лампочка не горит (29 сек) и когда она светится. То есть его значение будет равно 30 секундам.

Скважность такого процесса подсчитывается очень просто и представляется в удобном для записи виде. Это будет 30/1=30. А выражение для коэффициента заполнения придется представить в виде длинной строчки из цифр в десятичном представлении (1/30=0,03333333). Из сравнения двух форм представления нужной величины сразу видно, какая из них удобнее применительно к бытовой практике.

Особенности учета скважности в устройствах с ШИМ

Вопрос учета скважности особо важен при рассмотрении способа кодированной обработки сигнала, который называется «широтно-импульсная модуляция» и сокращенно обозначается как ШИМ. Основная суть этого метода кодировки состоит в изменении длительности импульса или его ширины по определенному закону, заданному условиями модуляции.

Подобная обработка сигнала как раз и относится к его скважности, которая в данном случае имеет не фиксированное значение, а постоянно меняется во времени. В методе обработки ШИМ изменения этого параметра означают либо сужение активной части импульса, либо ее расширение.

Плавные колебания его ширины рассматриваются по отношению к периоду сигнала, который в данном случае фиксирован по условиям работы устройства. Переменная скважность в ШИМ – типичный пример важности этой характеристики при проектировании и построении современных цифровых схем.

Где еще учитывается скважность в электронике

Этому показателю придается большое значение при проектировании следующих электронных узлов, входящих в состав сложных устройств:

Тактовые генераторы цифровых интегральных схем.
Контрольные электронные устройства.
Задающие генераторы в радиопередающих и радиоприемных устройствах.
Модули измерительной аппаратуры.

В первом примере скважность учитывается при тактировании работы компьютерных модулей и процессора, а во втором – она определяет частоту опроса (сканирования) контрольных датчиков.

В современных задающих генераторах приемо-передающей аппаратуры от импульсной последовательности задающего цифрового блока зависит корректность выставления несущей частоты ВЧ колебаний. В измерительных приборах от правильно выбранной скважности последовательности тактовых импульсов зависит точность снятия показаний.

Формирователи импульсов различной формы и скважности

Для формирования импульсов прямоугольной формы применяются специальные генераторные схемы, построенные на основе аналоговых или цифровых элементов. Для увеличения их мощности на выходе генераторов устанавливаются импульсные ключи на транзисторах, работающих в режиме насыщения.

Этот режим предполагает нахождение полупроводникового элемента в одном из двух возможных состояний («открыт» или «закрыт»). Первое соответствует активной части импульсных сигналов (их вершине), а второе – паузе между ними.

Для получения нужной скважности формируемой последовательности импульсов их длительность регулируется специальной электронной схемой, построенной на микроконтроллере.

Пример формирования импульсного светового сигнала в быту

Параметры импульсных сигналов, как правило, зависят от типа источника, но в жизни известны случаи их неявного проявления и воздействия на человека. В качестве примера обычно рассматривают свет от лампочки накаливания, которая излучает световой сигнал (загорается) с частотой электросети, равной 50 Герц. Однако человеческий глаз ощущает его как непрерывный, что объясняется инерционностью нашего зрения.

В результате этого оно воспринимает импульсные сигналы как сплошной световой поток. Единственное, на что наш глаз реагирует как положено – градации яркости свечения лампочки. Эта возможность как раз и реализуется за счет изменения скважности невидимых для нас импульсов. Аналогичным образом действуют электродвигатели постоянного тока, при своем вращении сглаживающие управляющие импульсы ШИМ. За счет изменения их скважности удается либо увеличивать частоту оборотов вала, либо уменьшать ее.

Что такое скважность

Скважностью называют безразмерную физическую величину, характеризующую любую импульсную систему. Она обозначается буквой S и определяется отношением периода импульсных сигналов T к их длительности. Кроме того существует так же величина обратная скважности, ее называют коэффициентом заполнения и обозначают буквой D, а по-английски она называется Duty cycle. Если длина импульса равна половине периода, то скважность равна двум, такой сигнал называется меандром. Длительность такого импульса и паузы между имульсами в периоде равны. Скважность может выражаться в процентах и является важной характеристикой импульсной системы, поскольку определяет отношение пиковой мощности импульсной установки к ее средней мощности. Недостаточно высокая скважность систем дискретной обработки информации приводит к ее искажению.