Система СИ была принята XI Генеральной конференцией по мерам и весам, некоторые последующие конференции внесли в СИ ряд изменений.
Система СИ определяет семь основных и производные единицы измерения, а также набор приставок . Установлены стандартные сокращённые обозначения для единиц измерения и правила записи производных единиц.
В России действует ГОСТ 8.417-2002, предписывающий обязательное использование СИ. В нем перечислены единицы измерения, приведены их русские и международные названия и установлены правила их применения. По этим правилам в международных документах и на шкалах приборов допускается использовать только международные обозначения. Во внутренних документах и публикациях можно использовать либо международные либо русские обозначения (но не те и другие одновременно).
Основные единицы : килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других.
Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в Системе СИ присвоены собственные названия.
Приставки можно использовать перед названиями единиц измерения; они означают, что единицу измерения нужно умножить или разделить на определенное целое число, степень числа 10. Например приставка «кило» означает умножение на 1000 (километр = 1000 метров). Приставки СИ называют также десятичными приставками.
История
Система СИ основана на метрической системе мер, которая была создана французскими учеными и впервые была широко внедрена после Великой Французской революции. До введения метрической системы, единицы измерения выбирались случайно и независимо друг от друга. Поэтому пересчет из одной единицы измерения в другую был сложным. К тому же в разных местах применялись разные единицы измерения, иногда с одинаковыми названиями. Метрическая система должна была стать удобной и единой системой мер и весов.
В 1799 г. были утверждены два эталона — для единицы измерения длины ( метр) и для единицы измерения веса ( килограмм).
В 1874 г. была введена система СГС, основанная на трех единицах измерения — сантиметр, грамм и секунда. Были также введены десятичные приставки от микро до мега.
В 1889 г. 1-ая Генеральная конференция по мерам и весам приняла систему мер, сходную с СГС, но основанную на метре, килограмме и секунде, т. к. эти единицы были признаны более удобными для практического использования.
В последующем были введены базовые единицы для измерения физических величин в области электричества и оптики.
В 1960 г. XI Генеральная конференция по мерам и весам приняла стандарт, который впервые получил название «Международная система единиц (СИ)».
В 1971 г. IV Генеральная конференция по мерам и весам внесла изменения в СИ, добавив, в частности, единицу измерения количества вещества ( моль).
Перевод единиц измерения | Физика | TutorOnline
В настоящее время СИ принята в качестве законной системы единиц измерения большинством стран мира и почти всегда используется в области науки (даже в тех странах, которые не приняли СИ).
Единицы системы СИ
После обозначений единиц Системы СИ и их производных точка не ставится, в отличие от обычных сокращений.
Основные единицы
| Длина | метр | metre (meter) | м | m |
| Масса | килограмм | kilogram | кг | kg |
| Время | секунда | second | с | s |
| Сила электрического тока | ампер | ampere | А | A |
| Термодинамическая температура | кельвин | kelvin | К | K |
| Сила света | кандела | candela | кд | cd |
| Количество вещества | моль | mole | моль | mol |
Производные единицы
Производные единицы могут быть выражены через основные с помощью математических операций умножения и деления. Некоторым из производных единиц, для удобства, присвоены собственные названия, такие единицы тоже можно использовать в математических выражениях для образования других производных единиц.
Математическое выражение для производной единицы измерения вытекает из физического закона, с помощью которого эта единица измерения определяется или определения физической величины, для которой она вводится. Например, скорость — это расстояние, которое тело проходит в единицу времени. Соответственно, единица измерения скорости — м/с (метр в секунду).
Часто одна и та же единица измерения может быть записана по разному, с помощью разного набора основных и производных единиц (см., например, последнюю колонку в таблице Производные единицы с собственными названиями ). Однако, на практике используются установленные (или просто общепринятые) выражения, которые наилучшим образом отражают физический смысл измеряемой величины. Например, для записи значения момента силы следует использовать Н×м, и не следует использовать м×Н или Дж.
| Плоский угол | радиан | radian | рад | rad | м×м -1 = 1 |
| Телесный угол | стерадиан | steradian | ср | sr | м 2 ×м -2 = 1 |
| Температура по шкале Цельсия | градус Цельсия | °C | degree Celsius | °C | K |
| Частота | герц | hertz | Гц | Hz | с -1 |
| Сила | ньютон | newton | Н | N | кг×м/c 2 |
| Энергия | джоуль | joule | Дж | J | Н×м = кг×м 2 /c 2 |
| Мощность | ватт | watt | Вт | W | Дж/с = кг×м 2 /c 3 |
| Давление | паскаль | pascal | Па | Pa | Н/м 2 = кг?м -1 ?с 2 |
| Световой поток | люмен | lumen | лм | lm | кд×ср |
| Освещённость | люкс | lux | лк | lx | лм/м 2 = кд×ср×м -2 |
| Электрический заряд | кулон | coulomb | Кл | C | А×с |
| Разница потенциалов | вольт | volt | В | V | Дж/Кл = кг×м 2 ×с -3 ×А -1 |
| Сопротивление | ом | ohm | Ом | Ω | В/А = кг×м 2 ×с -3 ×А -2 |
| Ёмкость | фарад | farad | Ф | F | Кл/В = кг -1 ×м -2 ×с 4 ×А 2 |
| Магнитный поток | вебер | weber | Вб | Wb | кг×м 2 ×с -2 ×А -1 |
| Магнитная индукция | тесла | tesla | Тл | T | Вб/м 2 = кг×с -2 ×А -1 |
| Индуктивность | генри | henry | Гн | H | кг×м 2 ×с -2 ×А -2 |
| Электрическая проводимость | сименс | siemens | См | S | Ом -1 = кг -1 ×м -2 ×с 3 А 2 |
| Радиоактивность | беккерель | becquerel | Бк | Bq | с -1 |
| Поглощённая доза ионизирующего излучения | грэй | gray | Гр | Gy | Дж/кг = м 2 /c 2 |
| Эффективная доза ионизирующего излучения | зиверт | sievert | Зв | Sv | Дж/кг = м 2 /c 2 |
| Активность катализатора | катал | katal | кат | kat | mol×s -1 |
Единицы, не входящие в Систему СИ
Некоторые единицы измерения, не входящие в Систему СИ, по решению Генеральной конференции по мерам и весам «допускаются для использования совместно с СИ».
| минута | minute | мин | min | 60 с |
| час | hour | ч | h | 60 мин = 3600 с |
| сутки | day | сут | d | 24 ч = 86 400 с |
| градус | degree | ° | ° | (П/180) рад |
| угловая минута | minute | ′ | ′ | (1/60)° = (П/10 800) |
| угловая секунда | second | ″ | ″ | (1/60)′ = (П/648 000) |
| литр | litre (liter) | л | l, L | 1 дм 3 |
| тонна | tonne | т | t | 1000 кг |
| непер | neper | Нп | Np | |
| бел | bel | Б | B | |
| электронвольт | electronvolt | эВ | eV | 10 -19 Дж |
| атомная единица массы | unified atomic mass unit | а. е. м. | u | =1,49597870691 -27 кг |
| астрономическая единица | astronomical unit | а. е. | ua | 10 11 м |
| морская миля | nautical mile | миля | 1852 м (точно) | |
| узел | knot | уз | 1 морская миля в час = (1852/3600) м/с | |
| ар | are | а | a | 10 2 м 2 |
| гектар | hectare | га | ha | 10 4 м 2 |
| бар | bar | бар | bar | 10 5 Па |
| ангстрем | ångström | Å | Å | 10 -10 м |
| барн | barn | б | b | 10 -28 м 2 |
Приставки СИ для образования десятичных и дольных единиц
| экса | Э | E | 10 18 |
| пета | П | P | 10 15 |
| тера | Т | Т | 10 12 |
| гига | Г | G | 10 9 |
| мега | М | М | 10 6 |
| кило | к | k | 10 |
| гекто | г | h | 10 2 |
| дека | да | da | 10 1 |
| деци | д | d | 10 -1 |
| санти | с | c | 10 -2 |
| милли | м | m | 10 -3 |
| микро | мк | m | 10 -6 |
| нано | н | n | 10 -9 |
| пикто | п | p | 10 -12 |
| фемто | ф | f | 10 -15 |
| атто | а | а | 10 -18 |
Объём

Объём, одна из основных величин, связанная с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов , т. е. кубов с рёбрами, равными единице длины. В СИ объём измеряется в м 3 .
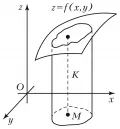
Задача вычисления объёмов простейших тел, идущая от практических потребностей, была одним из стимулов развития геометрии . Математика Древнего Востока (Вавилония, Египет) располагала рядом правил (большей частью эмпирических) для вычисления объёма тел, с которыми чаще всего приходилось встречаться на практике (например, призматических брусьев, пирамид полных и усечённых, цилиндров ). Среди формул для вычисления объёма были и неточные, дававшие не слишком заметную ошибку лишь в пределах употребительных размеров тела. Греческая математика последних столетий до н. э. освободила теорию вычисления объёма от приближённых эмпирических правил. В «Началах» Евклида и в сочинениях Архимеда имеются только точные правила для вычисления объёма многогранников и некоторых круглых тел (цилиндра, конуса , шара и их частей). При этом в создании учения об объёме многогранников греческие математики должны были преодолеть значительные трудности, существенно отличающие этот раздел геометрии от родственного ему раздела о площадях многоугольников. Источник различия, как выяснилось лишь в начале 20 в., состоит в следующем: в то время как всякий многоугольник можно посредством надлежащих прямолинейных разрезов и перекладывания полученных частей «перекроить» в квадрат, аналогичное преобразование (посредством плоских разрезов) произвольного многогранника в куб оказывается, вообще говоря, невозможным ( теорема Дена , 1901). Отсюда становится ясным, почему Евклид уже в случае треугольной пирамиды был вынужден прибегнуть к бесконечному процессу последовательных приближений, пользуясь при доказательстве методом исчерпывания . Бесконечный процесс лежит и в основе современной трактовки измерения объёма, сводящейся к следующему. Рассматриваются всевозможные многогранники, вписанные в тело K K K , и всевозможные многогранники, описанные вокруг тела K K K . Рис. 1. Объём. Рис. 1. Объём. Вычисление объёма многогранника сводится к вычислению объёмов составляющих его тетраэдров (треугольных пирамид). Пусть < V α > < V α >– множество чисел, состоящее из объёмов вписанных в тело многогранников, а < V β > < V β >– множество чисел, состоящее из объёмов описанных вокруг тела K K K многогранников. Множество < V α > < V α >ограничено сверху (например, объём любого описанного многогранника), а множество < V β > < V β >ограничено снизу (например, числом нуль). Наименьшее из чисел, ограничивающее сверху множество < V α > < V α >, называется нижним объёмом V ‾ underline V V тела K K K , а наибольшее из чисел, ограничивающее снизу множество < V β > < V β >, называется верхним объёмом V ‾ overline V V тела K K K . Если верхний объём тела K K K совпадает с его нижним объёмом V ‾ underline V V , то число V = V ‾ = V ‾ V=overline V= underline V V = V = V называется объёмом тела K K K , а само тело – кубируемым телом. Для того чтобы тело было кубируемым, необходимо и достаточно, чтобы для любого положительного числа ε varepsilon ε можно было указать такой описанный вокруг тела многогранник и такой вписанный в тело многогранник, разность V β − V α V_beta -V_alpha V β − V α объёмов которых была бы меньше ε varepsilon ε .
Аналитически объём может быть выражен с помощью кратных интегралов . Пусть тело K K K (рис. 1) ограничено цилиндрической поверхностью с параллельными оси O z Oz O z образующими, квадрируемой областью M M M плоскости O x y Oxy O x y и поверхностью z = f ( x , y ) z=f(x,y) z = f ( x , y ) , которую любая параллель к образующей цилиндра пересекает в одной и только в одной точке. Объём такого тела может быть вычислен с помощью двойного интеграла
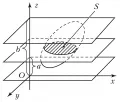
v = ∬ M f ( x , y ) d x d y . displaystyle v=iintlimits_M f(x,y)dxdy. v = M ∬ f ( x , y ) d x d y . Объём тела, ограниченного замкнутой поверхностью, которая пересекается с параллелями к оси O z Oz O z не более чем в двух точках, может быть вычислен как разность объёмов двух тел, подобных предшествующему. В общем случае объём тела может быть выражен в виде тройного интеграла v = ∭ d x d y d z , displaystyle v=iiint dxdydz, v = ∭ d x d y d z , Рис. 2. Объём. Рис. 2. Объём. где интегрирование распространяется на часть пространства, занятую телом. Иногда удобно вычислять объём тела через его поперечные сечения. Пусть тело, содержащееся между плоскостями z = a z=a z = a и z = b z=b z = b , b > a b>a b > a , рассекается плоскостями, параллельными оси O z Oz O z (рис. 2). Если все сечения тела квадрируемы и площадь сечения S = S ( z ) S=S(z) S = S ( z ) – непрерывная функция z z z , то объём тела может быть выражен интегралом V = ∫ a b S ( z ) d z . displaystyle V=int^_S(z)dz. V = ∫ a b S ( z ) d z . Об обобщениях понятия объёма см. в статье Мера множества .
Дубнов Яков Семёнович . Первая публикация: Большая российская энциклопедия, 2013.
Опубликовано 24 августа 2022 г. в 12:00 (GMT+3). Последнее обновление 24 августа 2022 г. в 12:00 (GMT+3). Связаться с редакцией
Единицы измерения объема
Единица СИ объема : [V] = кубический метр (м 3 ), кроме того: литр (л).
| 1 м 3 = 10 3 дм 3 = 10 6 см 3 = 10 9 мм 3 |
| 1 литр (л) = 1 дм 3 = 10 -3 м 3 |
Единицы измерения объема, не входящие в СИ
| 1 кубический ярд (ярд 3 ) = 27 фут 3 = 46656 дюйм 3 = 0.7646 м 3 |
| 1 кубический фут (фут 3 ) = 1728 дюйм 3 = 28.32 дм 3 |
| 1 кубический дюйм (дюйм 3 ) = 16.39 см 3 |
| 1 регистровая тонна = 100 фут 3 = 2.832 м 3 |
| 1 бушель = 8 гал [Британия] = 36.37 дм 3 |
| 1 галлон (гал) [Британия] = 4.546 дм 3 |
| 1 галлон (гал) [США] = 3.785 дм 3 |
По возможности следует избегать следующих сокращений:
куб. м для м 3 (кубический метр),
куб. дм для дм 3 (кубический дециметр),
куб. см для см 3 (кубический сантиметр),
куб. мм для мм 3 (кубический миллиметр).
Объем твердых тел неправильной формы может быть измерен либо по объему вытесненной жидкости, либо путем измерения выталкивающей силы в определенной жидкости.
США (сухие вещества)
- 1 Баррель [bl] = 115.627123584 дм³.
- 1 Бушель [bu] = 4 пекам = 8 галлонам = 32 квартам = 64 пинтам = 35.239072 дм³.
- 1 Пек [pk] = 8.80976778 дм³.
- 1 Галлон [gal] = 4.40488377086 дм³.
- 1 Кварта [qt] = 1.10122094272 дм³.
- 1 Пинта [pt] = 0.5506104713575 дм³.
- 1 Баррель [bl] = 163.65924 дм³.
- 1 Бушель [bu] = 36.36872 дм³.
- 1 Пек [pk] = 9.09218 дм³.
- 1 Галлон [gal] = 4.546090 дм³.
- 1 Кварта [qt] = 1.1365225 дм³.
- 1 Пинта [pt] = 0.56826125 дм³.
- 1 Унция [oz] = 28.413060625 см³.
Единицы измерения объема.
Объем ( V – от. лат. volume – объем, наполнение) – количественная характеристика пространства, занимаемого телом или веществом.
Объем (V – от. лат. volume – объем, наполнение) – количественная характеристика пространства, занимаемого телом или веществом. Объемом также обозначают вместимость, то есть объем внутреннего пространства сосуда и т.п. Объем тела или вместимость сосуда определяется его формой и линейными размерами.
Объем простых тел – это положительная величина, численное значение которой обладает следующими свойствами:
- равные тела имеют равные объемы,
- если тело разбито на части, являющиеся простыми телами, объем этого тела равен сумме объемов его частей,
- объем куба, ребро которого равно единице длины, равен единице.
Если ребро куба равно 1 см, то объем равен 1 см 3 , если ребро равно 1 м – то объем измеряется в 1 м 3 и т.д.
Система СИ. Международная система единиц измерения
Система СИ была принята XI Генеральной конференцией по мерам и весам, некоторые последующие конференции внесли в СИ ряд изменений.
Система СИ определяет семь основных и производные единицы измерения, а также набор приставок. Установлены стандартные сокращённые обозначения для единиц измерения и правила записи производных единиц.
В России действует ГОСТ 8.417-2002, предписывающий обязательное использование системы СИ. В нем перечислены единицы измерения, приведены их русские и международные названия и установлены правила их применения. По этим правилам в международных документах и на шкалах приборов допускается использовать только международные обозначения. Во внутренних документах и публикациях можно использовать либо международные либо русские обозначения (но не те и другие одновременно).
Основные единицы системы СИ: килограмм, метр, секунда, ампер, кельвин, моль и кандела. В рамках системы СИ считается, что эти единицы имеют независимую размерность, т. е. ни одна из основных единиц не может быть получена из других.
Производные единицы получаются из основных с помощью алгебраических действий, таких как умножение и деление. Некоторым из производных единиц в Системе СИ присвоены собственные названия.
Приставки можно использовать перед названиями единиц измерения; они означают, что единицу измерения нужно умножить или разделить на определенное целое число, степень числа 10. Например приставка «кило» означает умножение на 1000 (километр = 1000 метров). Приставки СИ называют также десятичными приставками.
Система СИ основана на метрической системе мер, которая была создана французскими учеными и впервые была широко внедрена после Великой Французской революции. До введения метрической системы, единицы измерения выбирались случайно и независимо друг от друга. Поэтому пересчет из одной единицы измерения в другую был сложным. К тому же в разных местах применялись разные единицы измерения, иногда с одинаковыми названиями. Метрическая система должна была стать удобной и единой системой мер и весов.
В 1799 г. были утверждены два эталона — для единицы измерения длины ( метр) и для единицы измерения веса ( килограмм).
В 1874 г. была введена система СГС, основанная на трех единицах измерения — сантиметр, грамм и секунда. Были также введены десятичные приставки от микро до мега.
В 1889 г. 1-ая Генеральная конференция по мерам и весам приняла систему мер, сходную с СГС, но основанную на метре, килограмме и секунде, т. к. эти единицы были признаны более удобными для практического использования.
В последующем были введены базовые единицы для измерения физических величин в области электричества и оптики.
В 1960 г. XI Генеральная конференция по мерам и весам приняла стандарт, который впервые получил название «Международная система единиц (СИ)».
В 1971 г. IV Генеральная конференция по мерам и весам внесла изменения в СИ, добавив, в частности, единицу измерения количества вещества ( моль).
В настоящее время система СИ принята в качестве законной системы единиц измерения большинством стран мира и почти всегда используется в области науки (даже в тех странах, которые не приняли СИ).
Меры и единицы объёма
Для пересчета единиц объема из одной размерности в другую можно воспользоваться данным конвертером. Здесь также представлены табличные данные о соотношении единиц объема (системных и внесистемных) в различных мерах.
![]()
Поделитесь информацией с друзьями
![]()
Скачать перечень калькуляторов
Таблица единиц объёма в метрической системе мер
| 1 см 3 | 1 000 мм 3 |
| 1 дм 3 (литр) | 1 000 см 3 |
| 1 дм 3 | 1 000 000 мм 3 |
| 1 м 3 | 1 000 дм 3 |
| 1 м 3 | 1 000 000 см 3 |
| 1 км 3 | 1 000 000 000 м 3 |
| 1 пинта | 0,56826125 л |
| 1 кварта | 2 пинты |
| 1 галлон | 8 пинт |
| 1 баррель | 158,988 л |
| 1 дюйм 3 | 16 387,064 мм 3 |
| 1 фут 3 | 1 728 дюймов 3 |
| 1 ярд 3 | 27 футов 3 |
| 1 ярд 3 | 46 656 дюймов 3 |
| 1 миля 3 | 5 451 776 000 ярдов 3 |




