Почему операция исключающее или называется сложением по модулю 2

Содержание

Иногда в некоторых задачах и формулах можно встретить странный знак — плюс в кружке: ⨁. Рассказываем, что он означает в математике и информатике.

В статье про сложение двух чисел с помощью транзистора мы говорили о логических операциях — И, ИЛИ и НЕ. Они работают с битами, то есть с нулями и единицами. Например, логическая операция НЕ меняет значение бита на противоположное — 1 меняет на 0 и наоборот.

Другие логические операции работают уже с двумя битами, они называются бинарными — например, логическое И, которое мы используем в половине наших проектов. Логика такая:

если оба числа — это единицы, то результат тоже будет единица, а во всех остальных случаях он будет равен нулю.

Логическое исключающее ИЛИ — это бинарная логическая операция, которая возвращает истину только тогда, когда одно из чисел — 1, а второе — 0. Обозначается так — XOR:

В информатике эту операцию ещё называется сложением по модулю 2, когда от результата откидывается всё, что кратно двум:

1 + 1 = 2 ← кратно двум, поэтому отбрасываем, и получается 1 ⨁ 1 = 0

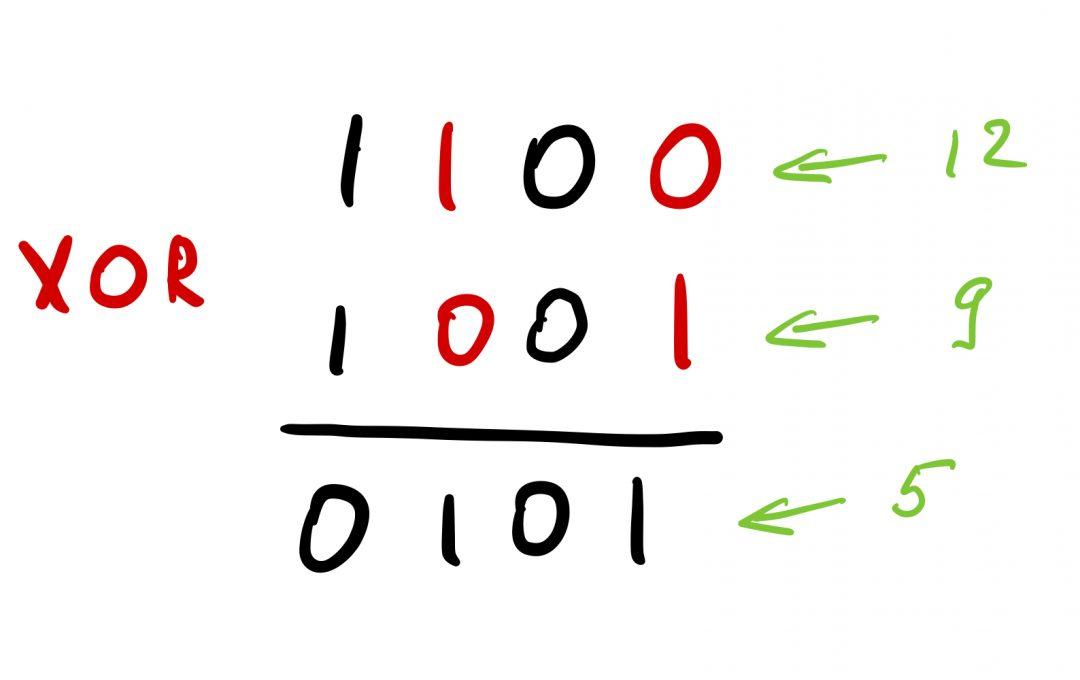
Чтобы было понятнее, как это работает, посчитаем 12 ⨁ 9 с точки зрения ИТ. Если непонятно, как из одного числа получается другое из нолей и единиц, почитайте нашу статью про двоичное счисление:

Переводим 12 в двоичный вид: 1100
Переводим 9 в двоичный вид: 1001
Побитово применяем XOR к каждому разряду и получаем 0101
Переводим 0101 в десятичный вид: 5
12 ⨁ 9 = 5

Математика: некий алгоритм расчёта

Иногда на собеседованиях дают такие задания на проверку логики:

Чему равно 7 ⨁ 3?

Если попробовать посчитать это как XOR, то результат не совпадёт с тем, что в ответах. Это значит, что плюсом в кружке обозначается некий алгоритм расчёта, в котором нам и нужно разобраться, чтобы решить задачу.

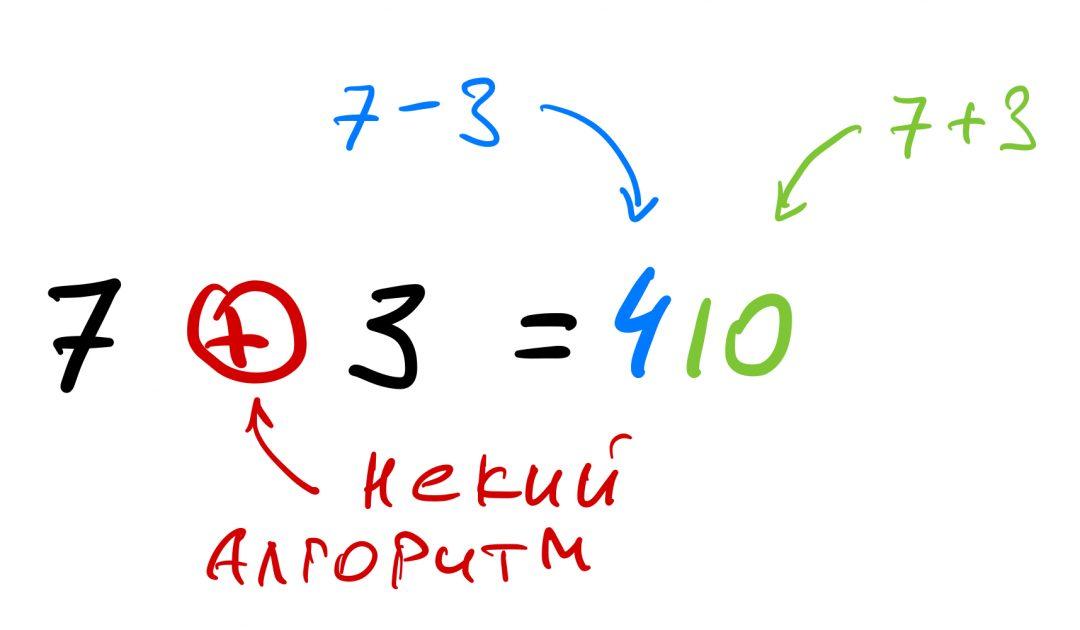
Алгоритм расчёта при этом может быть любым и включать в себя сколько угодно действий. В нашем случае он выглядит так:

Сначала из левого числа вычитается правое — так получается первое число в ответе:

А затем, наоборот, правое число складывается с левым — так получается второе число в ответе:

Получается, что правильное решение будет таким: 7 ⨁ 3 = 410

Функция сложения по модулю 2 (xor)

Завершая тему базисов следует отметить, что «джентльменский» набор функций языков программирования обычно включает конъюнкцию, дизъюнкцию, отрицание и «исключающее или». Ниже дана таблица истинности этих функций (вырезка из полной таблицы для всех функций):

Побитовое исключающее ИЛИ (сложение по модулю 2). Результат операции 42 ^ 30

Почему xor называется «сложение по модулю 2»? Потому что так оно и есть: в двоичной системе 0+0=0, 0+1=1+0=1, 1+1=10, а по модулю 2 (остаток от деления на 2) последняя сумма как раз и даёт 0.

Включение функции xor в джентльменский набор вызвано её замечательными свойствами. Во-первых, при инвертировании одного из аргументов эта функция также инвертируется. Во-вторых, эта функция показывает, когда аргументы не равны (а при инвертировании одного из аргументов — когда равны). В-третьих, она позволяет проводить управляемое инвертирование: при нулевом аргументе другой аргумент не меняется, при единичном же значении второй аргумент инвертируется. Наконец, эта функция инволютивна (её повторное применение возвращает к исходному аргументу): если (x3=x1 xor x2), то (x3 xor x1=x2) и (x3 xor x2=x1).

На последнем свойстве построен трюк с обменом значений двух переменных без использования третьей переменной (в C это записывается как «a^=b^=a^=b»). В графике эта функция применяется при выводе спрайтов на картинку — повторное её применение убирает спрайт с картинки. Также эта функция используется в криптографии — одна из схем заключается в наложении некоего кода на поток данных через функцию xor. Зашифрованный таким образом поток на исходный поток не похож, но может быть легко восстановлен повторным применением шифрующего кода.

На самом деле, функции «исключающее или», «неравнозначность» и «сложение по модулю 2» — разные функции, идентичные только в случае двух аргументов. Вот таблица истинности этих функций для трёх аргументов:

Почему операция исключающее или называется сложением по модулю 2

Нет аккаунта? Зарегистрироваться

Вступление

В математике обычное ИЛИ (включающее, OR ) встречается гораздо чаще исключающего (также называемого XOR ).

Например, когда Вы пишете выражение pVq, которое читается ”p ИЛИ q”, это так называемое включающее ИЛИ. В этом случае это выражение ИСТИНА ( true ), если p = ИСТИНА или q = ИСТИНА, или и p = ИСТИНА и q = ИСТИНА.

Включающее ИЛИ используется в обычном понимании операции ИЛИ ( OR ), оно используется чаще в логике, нежели исключающее ИЛИ ( XOR ).

Зачастую мы используем логику исключающего ИЛИ в предложениях. Например, если человек говорит: «Этим летом я поеду в Лондон или в Париж», он таким образом говорит нам, что хочет поехать либо в Лондон, либо в Париж, но не в оба. Даже если его заявление не кажется нам неверным,если он съездит в оба эти города, скорее всего иметься в ввиду будет поездка только в один из этих городов.

Вы можете подумать, что XOR не является интересным оператором. Он похож на OR, почему он должен быть интереснее чем OR?

Сначала приведём таблицу истинности операции XOR для булевых переменных:

Различные видения XOR

Мы можем увидеть XOR с различных сторон.

Предположим, что p и q — булевы переменные (переменные, которые могут принимать два взаимоисключающих значения (0 или 1, либо ИСТИНА И НЕИСТИНА, либо true и false )).

Также предположим, что p 1 , p 2 , p 3 … p n – булевы переменные.

Обозначим (+) операцию XOR (обозначается плюсом в кружочке). Тут мы имеем ввиду операцию XOR над булевыми переменными,а не побитовую операцию XOR , речь о побитовой XOR пойдёт немного дальше.

Для операций над булевыми переменными мы увидим, что:

p (+) q = true , если ТОЛЬКО ОДНА из переменных p и q равна true, это общепринятое определение XOR ;
p1 (+) p2 (+). (+) pn = true, если число переменных со значением true является нечётным, или равно false , если число переменных со значением true окажется чётным. Это как бы новое видение XOR, но еасли считать XOR ассоциативной операцией, то это является расширением предыдущего свойства.
p1 (+) p2 (+). (+) pn это тоже самое как сложение по модулю 2. Т.е. Если трактовать, что true == 1, а false == 0, то:

бинарная логика итд

Feb. 15th, 2012 at 4:40 PM

Двоичная логика (двузначная логика) — это логика, основанная на двух утверждениях. Истина (логическая единица) и ложь (логический нуль). Из-за простоты реализации получила широкое распространение в вычислительной технике. В вычислительной технике разделяют положительную (истина=1, ложь=0) и отрицательную (истина=0, ложь=1) логику.

В простейшей Булевой алгебре есть только два элемента, 0 и 1, и она определяется правилами:

XYX И Y

0	0	0
0	1	0
1	0	0
1	1	1

XYX ИЛИ Y

0	0	0
0	1	1
1	0	1
1	1	1

Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:

Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквивалентность («тогда и только тогда, когда»), импликация («следовательно»), сложение по модулю два («исключающее или»), штрих Шеффера , стрелка Пирса и другие.

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется вбитовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция приобретает смысл вычитания из единицы; — немодульного сложения; — равенства; — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR); — непревосходства суммы над 1 (то есть A B = (A + B)

Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний аксиом. Это позволило рассматривать, например, логику кубитов, тройственную логику (когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено») и др.

Свойства логических операций

Коммутативность: xy = yx, >.
Идемпотентность: xx = x, >.
Ассоциативность: (xy)z = x(yz), >.
Дистрибутивность конъюнкций и дизъюнкции относительно дизъюнкции, конъюнкции и суммы по модулю два соответственно:
,
,
.
Законы де Мо́ргана:
,
.
Законы поглощения:
,
.
Другие (1):
.
.
.
.
.
Другие (2):
.
.
.
Другие (3) (Дополнение законов де Мо́ргана):
.
.