Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом: F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц) .
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое к тому же может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой очень простых онлайн калькуляторов.
Онлайн калькулятор расчёта периода колебаний по частоте
А теперь всё то же самое, но наоборот:
Онлайн калькулятор расчёта частоты по периоду колебаний
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
 |  |
Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и,
наоборот – перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом: F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц) .
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое к тому же может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой очень простых онлайн калькуляторов.
Онлайн калькулятор расчёта периода колебаний по частоте
А теперь всё то же самое, но наоборот:
Онлайн калькулятор расчёта частоты по периоду колебаний
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
Период и частота обращения
Скорость при движении по окружности
При движении по окружности вместе со скоростью движения по траектории ($v$- линейная скорость) вводят угловую скорость ($omega $), которая характеризует быстроту изменения угла $varphi $:
Определим, какова связь между линейной и угловой скоростями. Длину дуги АМ ($s$) (рис.1) можно найти как:
тогда изменение длины дуги за время$ Delta t$ равно$ Delta s$:
[Delta s=RDelta varphi left(3right).]
Найдем отношение $frac$, разделив обе части выражения (3) на $Delta t$:
Перейдем к пределу в правой и левой частях равенства (4) при $Delta tto 0$, получим:
Ускорение материальной точки при движении по окружности
Величина нормальной (центростремительной) компоненты ускорения вычисляется при помощи формулы:
При равномерном перемещении по окружности величина центростремительного ускорения постоянна ($a_n=const). $Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Тангенциальное ускорение при движении по окружности вычисляют, как и при любом криволинейном движении:
Как связаны между собой частота колебаний и период?
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом: F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц) .
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое к тому же может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой очень простых онлайн калькуляторов.
Онлайн калькулятор расчёта периода колебаний по частоте
А теперь всё то же самое, но наоборот:
Онлайн калькулятор расчёта частоты по периоду колебаний
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
| | |
Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и,
наоборот – перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом: F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц) .
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое к тому же может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой очень простых онлайн калькуляторов.
Онлайн калькулятор расчёта периода колебаний по частоте
А теперь всё то же самое, но наоборот:
Онлайн калькулятор расчёта частоты по периоду колебаний
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
Период обращения тела при движении по окружности равен 1 мин чему равна частота обращения
Равномерное движение по окружности характеризуют периодом и частотой обращения.
Период обращения — это время, за которое совершается один оборот.
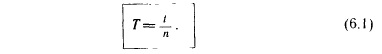
Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле:
Итак, чтобы найти период обращения, надо время, за которое совершено п оборотов, разделить на число оборотов.
Другой характеристикой равномерного движения по окружности является частота обращения.
Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:
Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.
За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с -1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.
Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому
Формулы (6.1) и (6.3) позволяют найти период обращения Т, если известны число n и время оборотов t или частота обращения V. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела V и радиус окружности r, по которой оно движется.
Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (lокр = 2 Пr, где П≈3,14- число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,
Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.
. 1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?
С.В. Громов, Н.А. Родина, Физика 8 класс
Отослано читателями из интернет-сайтов
Сборник конспектов уроков по физике, рефераты на тему из школьной программы. Календарно тематическое планирование. физика 8 класс онлайн, книги и учебники по физике. Школьнику подготовиться к уроку.
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Период обращения тела при движении по окружности равен 1 мин чему равна частота обращения
Задание №1629
Рассчитайте центростремительное ускорение, с которым по закруглению радиусом 250 м движется поезд со скоростью 36 км/ч.
Задание №1630
Найдите период и частоту обращения минутной стрелки.
Дано:
N = 1 оборот;
t = 60 мин.
Найти:
ν − ?
T − ?
СИ:
t = 3600 с.
Решение:
Найдем период обращения минутной стрелки:
$T = frac$;
$T = frac = 3600$ с = 60 мин.
Найдем частоту обращения минутной стрелки:
$ν = frac$;
$ν = frac = 2,8 * 10^ с^$.
Ответ: 60 мин.; $2,8 * 10^ с^$.
Задание №1631
Радиус колеса велосипеда равен 30 см. Определите линейную скорость вращения точек обода колеса, если колесо делает 100 оборотов в минуту.
Дано:
R = 30 см;
N = 100 оборотов;
t = 1 мин.
Найти:
v − ?
СИ:
R = 0,3 м;
t = 60 с.
Решение:
Найдем период обращения колеса:
$T = frac$;
$T = frac = 0,6$ с;
$v = frac$;
$v = frac = 3,1$ м/с.
Ответ: 3,1 м/с.
Задание №1632
Чему равны частота и период обращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов?
Дано:
N = 50 оборотов;
t = 2 мин.
Найти:
ν − ?
T − ?
СИ:
t = 120 с.
Решение:
Найдем период обращения колеса:
$T = frac$;
$T = frac = 2,4$ с;
Найдем частоту обращения:
$ν = frac$;
$ν = frac = 0,42 с^$.
Ответ: 2,4 с.; 0,42 $с^$.
Задание №1633
Радиус, описываемый секундной стрелкой, равен 10 см. Определите линейную скорость острия стрелки, частоту обращения и центростремительное ускорение.
Дано:
R = 10 см;
t = 60 с.
Найти:
$v_$ − ?
ν − ?
$a_$ − ?
СИ:
R = 0,1 м.
Решение:
За 60 секунд стрелка делает один полный оборот. Найдем частоту обращения секундной стрелки:
$ν = frac$;
$ν = frac = 0,017 с^$.
Найдем линейную скорость острия стрелки:
$v_ = frac$;
$v_ = frac = 0,01$ м/с;
Найдем центростремительное ускорение:
$a_ = frac>$;
$a_ = frac> = 0,001 м/с^$.
Ответ: ,017 с^$; 0,01 м/с; ,001 м/с^$.
Задание №1634
Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колёса локомотива, радиус которых 0,6 м?
Дано:
v = 72 км/ч;
t = 1 мин.;
R = 0,6 м.
Найти:
N − ?
СИ:
v = 20 м/с;
t = 60 с.
Решение:
Найдем период обращения колеса:
$v = frac$;
$T = frac$;
Найдем количество оборотов колеса в минуту:
$N = frac = frac<frac> =frac$;
$N = frac = 318$ об/мин.
Ответ: 318 об/мин.
Задание №1635
При точении деталей скорость резания достигает 240 м/мин. На какое число оборотов в минуту при этом нужно включить шпиндель токарного станка, если диаметр детали 100 мм?
Дано:
v = 240 м/мин.;
t = 1 мин.;
d = 100 мм.
Найти:
N − ?
СИ:
v = 4 м/с;
t = 60 с;
d = 0,1 м.
Решение:
d = 2R;
Найдем период обращения шпинделя токарного станка:
$v = frac = frac$;
$T = frac$;
Найдем количество оборотов шпинделя в минуту:
$N = frac = frac<frac> =frac$;
$N = frac = 764$ об/мин.
Ответ: 764 об/мин.
Задание №1636
Секундная стрелка часов в 4 раза короче минутной. Рассчитайте отношение скоростей концов стрелок.
Задание №1637
Тело движется по окружности радиусом 1 м. Чему равен период обращения тела по окружности, если центростремительное ускорение составляет 4 $м/с^$?
Дано:
R = 1 м;
$a_ = 4 м/с^$.
Найти:
T − ?
Решение:
Найдем скорость движения тела:
$a_ = frac$;
$v^ = a_ * R$;
$v = sqrt $;
$v = sqrt = 2$ м/с;
Найдем период обращения тела по окружности:
$v = frac$;
$T = frac$;
$T = frac = 3,14$ с.
Ответ: 3,14 с.
Задание №1638
При равномерном движении по окружности радиусом 0,1 м тело совершает 30 оборотов в минуту. Чему равно центростремительное ускорение?
Дано:
R = 0,1 м;
t = 1 мин.;
N = 30 оборотов.
Найти:
$a_$ − ?
СИ:
t = 60 с.
Решение:
Найдем период обращения тела:
$T = frac$;
Найдем скорость движения тела:
$v = frac = frac<frac> = frac$;
$v = frac = 0,314$ м/с;
Найдем центростремительное ускорение
$a_ = frac>$;
$a_ = frac> = 1 м/с^$.
Ответ: $1 м/с^$.
Задание №1639
При какой скорости движения автомобиля МАЗ − 200 его колесо диаметром 1,1 м вращается с частотой 310 об/мин?
Дано:
d = 1,1 м;
ν = 310 об/мин.
Найти:
v − ?
СИ:
ν = 5,17 об/с.
Решение:
Найдем период обращения тела:
$ν = frac$;
$T = frac$;
Найдем скорость движения тела:
d = 2R;
$v = frac = frac<frac> = πdν$;
v = 3,14 * 1,1 * 5,17 = 17,8 м/с = 64 км/ч.
Ответ: 64 км/ч.
Задание №1640
Период обращения первого искусственного спутника Земли был равен 96,2 мин. Сколько оборотов совершал спутник в минуту; в сутки?
Дано:
T = 96,2 мин.
$t_ = 1$ мин.;
$t_ = 1$ сутки.
Найти:
$N_$ − ?
$N_$ − ?
Решение:
Найдем количество оборотов спутника:
$T = frac$;
$N = frac$;
$N_ = frac = 0,01$ об/мин;
$t_ = 1$ сутки = 24 ч. * 60 мин. = 1440 мин.
$N_ = frac = 15$ об/сутки.
Ответ: 0,01 об/мин; 15 об/сутки.
Задание №1641
Какой путь проходит за сутки конец минутной стрелки Кремлёвских курантов, если длина стрелки 4,5 м?
Дано:
R = 4,5 м;
t = сутки;
T = 60 мин.
Найти:
l − ?
СИ:
t = 86400 с.;
T = 3600 с.
Решение:
Найдем скорость движения минутной стрелки:
$v = frac$;
Найдем путь, который проходит минутная стрелка:
$l = vt = frac$;
$l = frac = 678$ м.
Ответ: 678 м.
Задание №1642
Заднее колесо трактора, диаметр которого равен 120 см, сделало 520 оборотов. Сколько оборотов сделало на том же расстоянии переднее колесо диаметром 64 см?
Дано:
$d_ = 120$ см;
$N_ = 520$ оборотов;
$d_ = 64$ см;
$S_ = S_$.
Найти:
$N_$ − ?
СИ:
$d_ = 1,2$ м;
$d_ = 0,64$ м.
Решение:
Длина окружности колеса равна:
l = πd;
Расстояние, которое проходит колесо, равно:
S = lN = πdN;
Т.к. $S_ = S_$, то
$πd_N_ = πd_N_$;
$N_ = frac<πd_N_><πd_> = frac$;
$N_ = frac = 975$ оборотов.
Ответ: 975 оборотов.
Задание №1643
Шарик на нити длиной 20 см равномерно вращается в вертикальной плоскости. Чему равно центростремительное ускорение шарика, если за 2 мин он делает 60 оборотов?
Дано:
R = 20 см;
t = 2 мин;
N = 60 оборотов.
Найти:
$a_$ − ?
СИ:
R = 0,2 м;
t = 120 с.
Решение:
Найдем период обращения тела:
$T = frac$;
Найдем скорость движения тела:
$v = frac = frac<frac> = frac$;
$v = frac = 0,628$ м/с;
Найдем центростремительное ускорение
$a_ = frac>$;
$a_ = frac> = 2 м/с^$.
Ответ: $2 м/с^$.
- Вы здесь:
- 7 класс
- Физика
- ГДЗ ответы к сборнику вопросов и задач по физике к учебникам 7-9 класс Перышкина, Гутник (Марон, Позойский)
- ГДЗ ответы физика 7 класс Ханнанова, рабочая тетрадь к учебнику Перышкина
- ГДЗ ответы по физике 7 класс к учебнику Перышкин, Дрофа
Частота обращения
Движение тела (точки) по окружности можно характеризовать еще одной величиной — числом оборотов по окружности в единицу времени. Ее называют частотой обращения и обозначают буквой п. Она очень просто связана с периодом обращения Т. Если, например, период обращения равен 0,1 с, то за 1 с тело совершает 10 оборотов. Так что частота — это величина, обратная периоду:
Единица частоты — это 1:с, или с _1 .
Скорость v движения тела по окружности можно выразить и через
частоту п. В самом деле, при одном обороте тело проходит путь, равный2π r, где г — радиус окружности. Значит, при п оборотах тело пройдет за 1 с путь, равный 2π rп. Следовательно, v= 2π rп. Подставив это выражение в формулу (3) предыдущего параграфа, мы получим для центростремительного ускорения еще одну формулу:
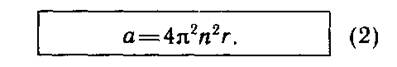
О зависимости центростремительного ускорения от радиуса окружности. Согласно формуле (3) § 15 центростремительное ускорение обратно пропорционально радиусу окружности r. По формулам же (1) и (2) этого параграфа оно прямо пропорционально радиусу. Это может показаться странным. Но никакого противоречия здесь нет. Мы знаем, что центростремительное ускорение пропорционально квадрату скорости Но если скорость выразить через частоту п или период Т (v= 2π rп; v = 2π r:Т) и подставить в формулу то это и приводит к формулам (1) и (2), по которым центростремительное ускорение пропорционально радиусу.
При решении задач можно пользоваться любой из трех формул для центростремительного ускорения — формулой (3) § 15 и формулами (1) и (2) этого параграфа.
| | | следующая лекция ==> | |
| Период обращения | | | Равномерное движение по окружности |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2024) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.011 сек. —>
Период обращения тела по окружности равен 1ч. чему равна частота обращения?
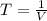, где Т-период, V(ню)-частота.
или Гц, переводим 1 час в секунды:
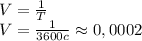Гц
4,8(100 оценок)
t₂ = 100°C — температура кипения воды
с = 4200 Дж/(кг·град) — удельная теплоёмкость воды
ρ = 1000 кг/м³ — плотность воды
q = 30·10⁶ Дж/кг — удельная теплота сгорания древесного угля
m — ? — масса древесного угля
Энергия, полученная при сгорании древесного угля
Энергия, необходимая для нагрева воды
Уравнение энергетического баланса
m = 4200 · 1000 · 0.006 · (100 — 20) : 30·10⁶
m = 0.0672 кг = 67,2 г
4,8(79 оценок)
Притяжение незаряженных тел из диэлектриков к заряженным телам объясняется их к поляризации.
Поляризация – явление смещения связанных электрических зарядов внутри атомов, молекул или внутри кристаллов под действием внешнего электрического поля. Самый простой пример поляризации – действие внешнего электрического поля на нейтральный атом. Во внешнем электрическом поле сила, действующая на отрицательно заряженную оболочку, направлена противоположно силе, которая действует на положительное ядро. Под действием этих сил электронная оболочка несколько смещается относительно ядра и деформируется. Атом остаётся в целом нейтральным, но центры положительного и отрицательного заряда в нём уже не совпадают. Такой атом можно рассматривать как систему из двух равных по модулю точечных зарядов противоположного знака, которую называют диполем.
