Обозначение логических операций в информатике

Содержание

На данной странице будут рассмотренны 5 логических операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность, которых Вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции. Советуем Вам воспользоваться нашими программами для решения задач по математике, геометрии и теории вероятности. Помоми большого количества программ для решения задач на сайте работает форум, на котором Вы всегда можете задать вопрос и на котором Вам всегда помогуть с решением задач. Пользуйтесь нашими сервисами на здоровье!

Высказывание — это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).

Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.

Логическое выражение — устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).

Сложное логическое выражение — логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.

Логические операции и таблицы истинности

1) Логическое умножение или конъюнкция:

Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A

дизъюнкция;

конъюнкция;

строгая дизъюнкция;

импликация;

эквивалентность.

В программировании также стоит обратить внимание на запись исключающего или. Это – операция XOR.

Импликация или логическое следование

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть, данная логическая операция связывает два простых логических выражения, из которых первое является условием ($A$), а второе ($A$) является следствием условия ($A$).

Обозначения: $to$, $Rightarrow$.

Таблица истинности для импликации

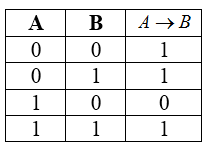
$A to B = ¬A vee B$.
Импликация $A to B$ ложна, если $A=1$ и $B=0$.
Если $A=0$, то импликация $A to B$ истинна при любом значении $B$, (из лжи может следовать истинна).

Эквивалентность или логическая равнозначность

Эквивалентность — это сложное логическое выражение, которое истинно на равных значениях переменных $A$ и $B$.

ИНФОРМАТИКА 8 класс: Свойства логических операций

Обозначения: $leftrightarrow$, $Leftrightarrow$, $equiv$.

Таблица истинности для эквивалентности

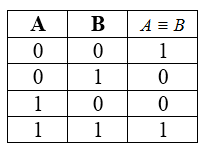
Эквивалентность истинна на равных наборах значений переменных $A$ и $B$.
КНФ $A equiv B = (bar vee B) cdot (A cdot bar)$
ДНФ $A equiv B = bar cdot bar vee A cdot B$

Логика

f) символ 1 используется для обозначения истины (истинного высказывания); символ 0 – для обозначения лжи (ложного высказывания).

1.2. Два логических выражения, содержащих переменные, называются равносильными (эквивалентными), если значения этих выражений совпадают при любых значениях переменных. Так, выражения А → В и (¬А) / В равносильны, а А / В и А / В – нет (значения выражений разные, например, при А = 1, В = 0).

1.3. Приоритеты логических операций: инверсия (отрицание), конъюнкция (логическое умножение), дизъюнкция (логическое сложение), импликация (следование), тождество. Таким образом, ¬А / В / С / D означает то же, что и

Возможна запись А / В / С вместо (А / В) / С. То же относится и к конъюнкции: возможна запись А / В / С вместо (А / В) / С.

2. Свойства

Приведенный ниже список НЕ претендует на полноту, но, надеемся, достаточно представителен.

2.1. Общие свойства

Для набора из n логических переменных существует ровно 2n различных значений. Таблица истинности для логического выражения от n переменных содержит n+1 столбец и 2n строк.

2.2.Дизъюнкция

Если хоть одно из подвыражений, к которым применяется дизъюнкция, истинно на некотором наборе значений переменных, то и вся дизъюнкция истинна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то дизъюнкция этих выражений тоже ложна.
Значение дизъюнкции не зависит от порядка записи подвыражений, к которым она применяется.

2.3. Конъюнкция

Если хоть одно из подвыражений, к которым применяется конъюнкция, ложно на некотором наборе значений переменных, то и вся конъюнкция ложна для этого набора значений.
Если все выражения из некоторого списка истинны на некотором наборе значений переменных, то конъюнкция этих выражений тоже истинна.
Если все выражения из некоторого списка ложны на некотором наборе значений переменных, то конъюнкция этих выражений тоже ложна.
Значение конюнкции не зависит от порядка записи подвыражений, к которым она применяется.

2.4. Простые дизъюнкции и конъюнкции

Назовем (для удобства) конъюнкцию простой, если подвыражения, к которым применяется конъюнкция, – различные переменные или их отрицания. Аналогично, дизъюнкция называется простой, если подвыражения, к которым применяется дизъюнкция, – различные переменные или их отрицания.

Простая конъюнкция принимает значение 1 (истина) ровно на одном наборе значений переменных.
Простая дизъюнкция принимает значение 0 (ложь) ровно на одном наборе значений переменных.

2.5. Импликация

Импликация A →B равносильна дизъюнкции (¬А) / В. Эту дизъюнкцию можно записать и так: ¬А / В.
Импликация A →B принимает значение 0 (ложь) только если A=1 и B=0. Если A=0, то импликация A →B истинна при любом значении B.

Общие сведения

Одним из простых типов данных в информатике считается булевый. Этот примитивный вид может принимать два возможных значения истинный или ложный. В международной системе для описания используются слова true и false. Своё название тип получил благодаря английскому математику Джорджу Буля изучающий логику математических операций. В общем случае под ним понимают действие, соответствующее некому высказыванию. То есть с её помощью получают сложные выражения из простых и используют результат для управления последовательности определённых программ.

Наиболее часто в языках программирования применяется числовой тип описания. В них считается, что ноль соответствует логической лжи, а единица — истинности. Это даёт возможность использовать действия, выбрав отдельные биты с помощью побитовых операций. Среди них наиболее известны следующие:

конъюнкция — действие по смыслу приближённое к логическому умножению и союзу «и»;
дизъюнкция — сложение напоминающее сравнение «или», то есть «или то, или это, или оба одновременно»;
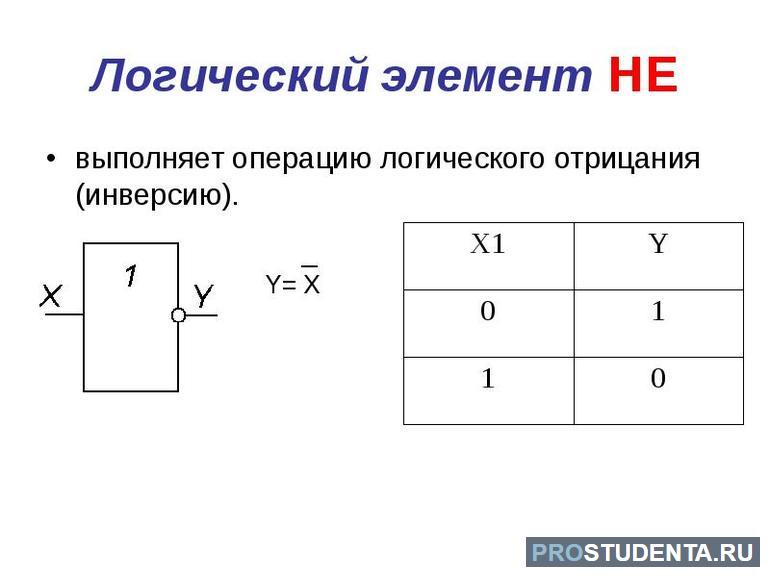
отрицание — операция над суждением с противоположным результатом начальному.

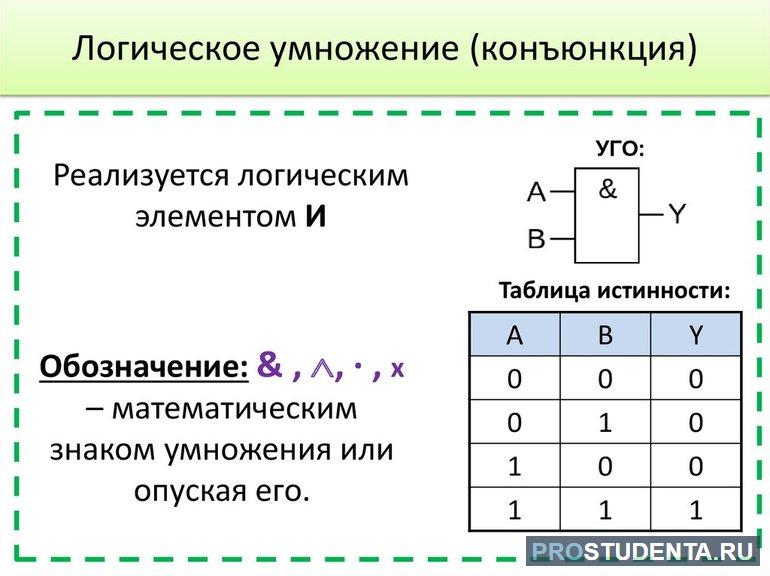
Последнее действие принято обозначать чертой, ставящейся над суждением. Кроме этого, могут использоваться операции исключающие «ИЛИ», эквивалентности, инверсии и сравнения. Но традиционным применением булевого типа считаются значения «да» / «нет».

Для реализации логических действий используются электрические схемы, называемые логическими элементами. В качестве данных используются сигналы с разным уровнем напряжения. На вход схемы подаётся значение, принимаемое за ноль или единицу, а с выхода снимается другое с определённым уровнем. То есть используется двоичная система счисления. Напряжение высокого значения принимается как истина, а низкого считается за ложь. Логические схемы позволяют в наглядном графическом виде отобразить последовательность операций при вычислении логических формул.

Такие логические элементы используют для организации работы компьютеров, схем автоматического контроля. Поэтому для любых видов сигналов характерны дискретные величины. При этом сам элемент может иметь как один, так и несколько входов, два или один выход. Традиционно элементы логики изготавливают в виде радиодеталей. Это интегральные микросхемы разного размера.

Таблица истинности

Любую логическую функцию можно описать с помощью таблицы истинности. То есть при выполнении действий их результатом будет два вида значение «истина» либо «ложь». Как оказалось, использовать таблицы для описания работы элементов довольно удобно. Причём вместо слов в ней ставят единицу либо ноль. Сложное логическое выражение обычно включает в себя несколько простых. Соединяет их операция.

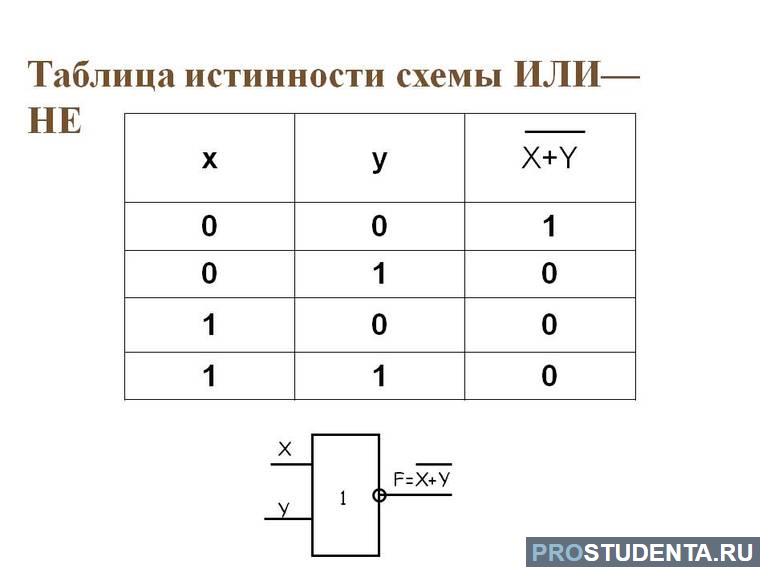
Таблица истинности содержит все возможные комбинации переменных на входе и соответствующий результат их на выходе. Состоит она из 2 n строк, где n — количество переменных, и n + m столбцов, у которых m — выходные данные. Если все строки известны, то исследуемый элемент, включающий функцию, называют частично определённый. Количество существующих операций зависит от числа высказываний. Если содержится 2 n строк, то и всевозможных комбинаций будет 2 n соответствующих значениям аргументов.

Строится таблица по простому принципу. В столбцах указываются номера входов и выходов, а строки заполняют соответствующими цифрами. Например, пусть имеется логический элемент с тремя выводами. Два из них входа X1 и X2, а один выход Y1. При подаче высокого напряжения сразу на два входных контакта на выходе устанавливается низкий уровень. В ином же случае всегда будет высокий. Для такой ситуации в первых двух столбцах проставляется все возможные варианты. Их будет четыре. В последней же колонке, советующей выходу, ставятся везде нули, кроме строчки, состоящей из двух единиц.

Построенная таблица является законченной основной характеристикой логического элемента. Работать с ней довольно удобно, так как наглядно и без дополнительных пояснений видно, какие сигналы установятся на выходе. Иногда есть смысл строить истинность для той или иной функции, используя лишь определённый набор заданных операций. Существует несколько возможностей описания:

дизъюнктивная;
конъюнктивная;
алгебраическая нормальная.

Простой конъюнкцией называется система переменных, где каждая из них встречается только один раз. Если же объединить дизъюнкции с помощью конъюнкции, то можно получить совершённую конъюнктивную нормальную форму. В обратном случае возникнет дизъюнктивная составляющая.

3.3. Построение таблиц истинности для логических выражений

Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:

подсчитать n — число переменных в выражении;
подсчитать общее число логических операций в выражении;
установить последовательность выполнения логических операций с учётом скобок и приоритетов;
определить число столбцов в таблице: число переменных + число операций;
заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
определить число строк в таблице (не считая шапки таблицы) m = 2n;
выписать наборы входных переменных с учётом того, что они представляют собой целый ряд n—разрядных двоичных чисел от 0 до 2 n — 1;
провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.

Построим таблицу истинности для логического выражения A ∨ А Б равносильно логическому выражению А.