Максимальная сила тока протекающего через катушку формула

Содержание

Чему равна максимальная сила тока, протекающего через колебательный контур с катушкой, имеющей индуктивность 6 мкГн и конденсатором ёмкостью 40 пФ?

Тема: Расчет максимальной силы тока в колебательном контуре

Объяснение:
Чтобы найти максимальную силу тока в колебательном контуре, используем формулу:

Где:
— — максимальная сила тока
— — напряжение в колебательном контуре
— — импеданс колебательного контура
— — сопротивление в колебательном контуре
— — ёмкость конденсатора
— — индуктивность катушки
— — угловая частота, равная 1/√(LC)

Переведем данные в соответствующие единицы измерения. Заменим значения в формуле и произведем вычисления, чтобы найти максимальную силу тока.

Пример использования:
Дано:
— Ф
— Гн

Решение:
Переводим значения в базовые единицы:
— Ф = 40 пФ = 40times10^ Ф.
— Гн = 6 мкГн = 6times10^ Гн.

Подставляем значения в формулу:
—

Совет:
Чтобы лучше понять колебательные контуры, рекомендуется изучить основные понятия по физике и электротехнике, такие как сопротивление, ёмкость и индуктивность. Это поможет вам лучше разобраться в этой формуле и применить ее на практике.

Упражнение:
Найдите максимальную силу тока в колебательном контуре с конденсатором ёмкостью 20 нФ и катушкой с индуктивностью 8 мкГн, если напряжение в контуре равно 12 В.

Колебательный контур

Колебательный контур ― это электрическая цепь, содержащая катушку индуктивности и конденсатор. В такой электрической цепи происходят колебания электрического тока и напряжения, и взаимная трансформация энергии электрического поля и энергии магнитного поля.

Процессы в колебательном контуре У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.

Если в цепи, кроме проводов и резисторов, находится катушка индуктивности, в равномерный и быстрый процесс перераспределения заряда вмешивается ЭДС самоиндукции катушки. Согласно правилу Ленца, втекающий в катушку ток вызывает ЭДС самоиндукции ― а ЭДС самоиндукции создает индуцированный ток, направленный так, чтобы препятствовать изменению тока в цепи. Если ток в цепи вдруг резко увеличивается ― индукционный ток стремиться его уменьшить, если ток в сети вдруг уменьшается ― индукционный ток стремиться его увеличивать.

катушка индуктивности в цепях постоянного и переменного тока

Поэтому из―за катушки индуктивности заряд не переходит сразу через всю цепь, от одной обкладки конденсатора к другой. Сила тока в цепи медленно увеличивается ― потому что ее быстрому росту препятствует ЭДС самоиндукции катушки. Максимальной сила тока становится в тот момент, когда конденсатор разряжен (обе его обкладки обладают нулевым зарядом). В этот момент сила тока максимальна благодаря тому, что как только ее перестает наращивать конденсатор за счет потерянных зарядов ― ЭДС самоиндукции прекращает ей препятствовать.

Но разряженный конденсатор больше не может поддерживать силу току ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.

После того как конденсатор зарядиться ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.

Параллельный и последовательный колебательный контур

Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных параметров. Онлайн калькулятор резонансной частоты колебательного контура, добротности и коэффициента затухания в зависимости от величин индуктивности, ёмкости и сопротивления потерь

Колебательный контур – это пассивная электрическая цепь, которая состоит из конденсатора и катушки индуктивности, в которой возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный контур называется последовательным.

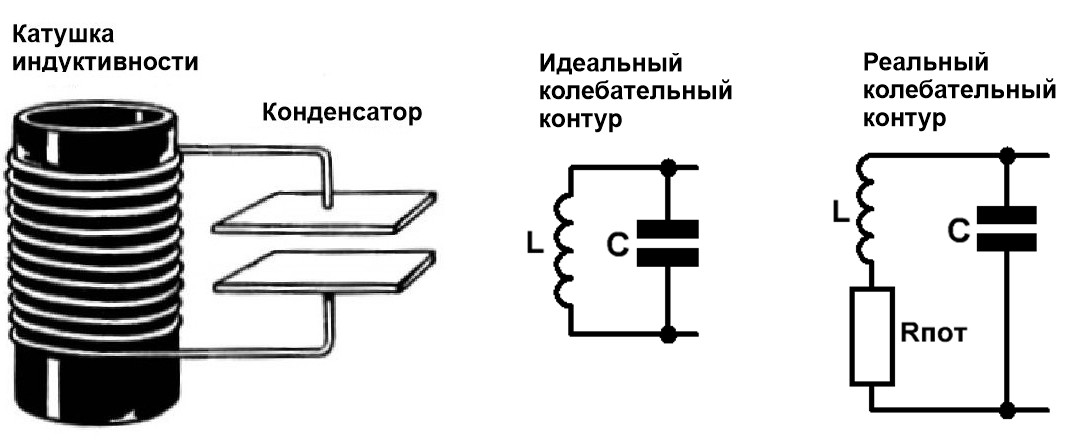
Для начала давайте рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного.

Рис.1 Параллельный колебательный контур, его изображение на схеме
(идеальный колебательный контур), реальный колебательный контур

При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного сопротивления потерь катушки – Rпот . Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.

Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)

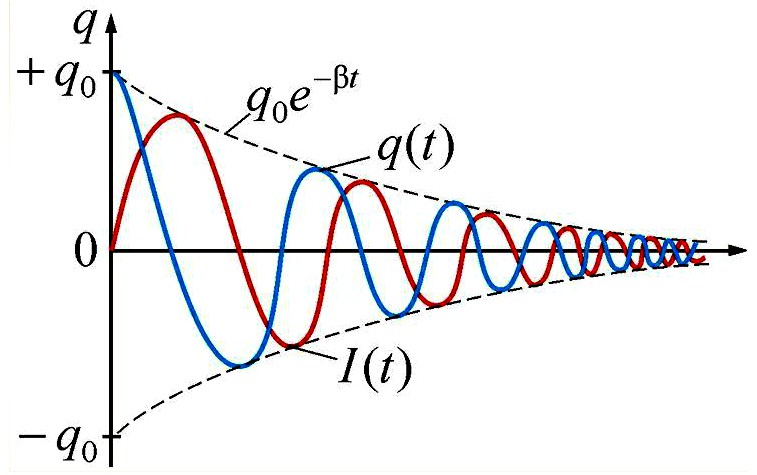
Рис.2 Колебательный процесс в параллельном колебательном контуре

Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд qmax от внешнего источника Bat напряже- нием Umax . После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).

Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь, суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.

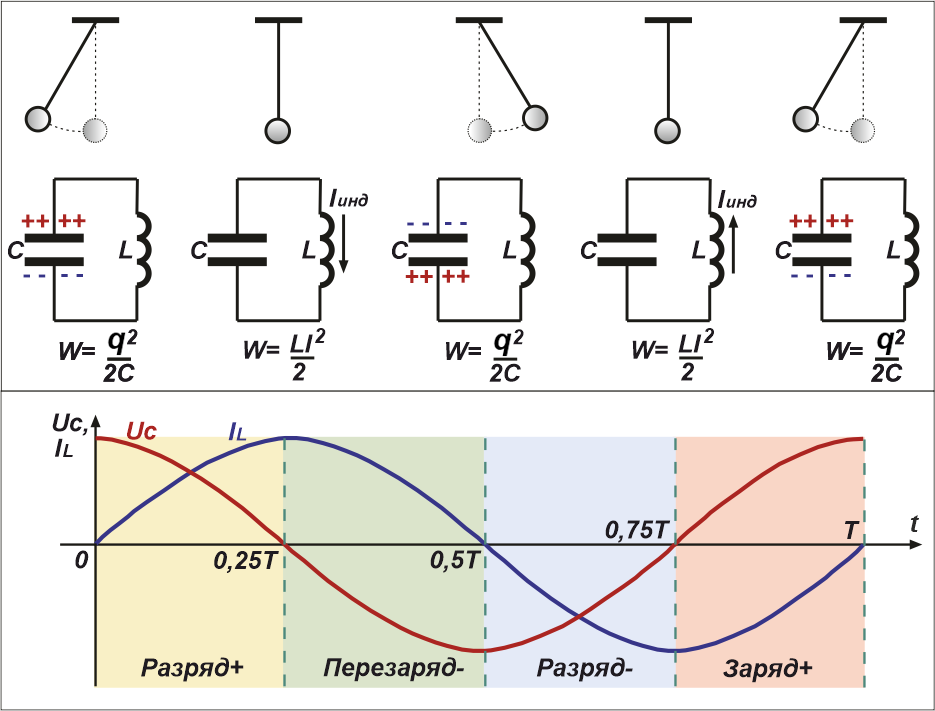
Рис.3 Фазы колебаний в колебательном контуре за полный период

Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.

Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна W = q 2 /2C ). Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС самоиндукции, препятствующая этому росту.
2. t = 0.25Т – конденсатор полностью разряжен. Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки W = L*I 2 /2 . Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0.5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0.75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.

А теперь: Формулы для расчёта колебательного LC контура:

Период колебаний: T0 = 2π√ LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 = 2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура: ;

Мгновенные значения напряжения, тока и энергии рассчитываются по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) .

Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров (с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания β и логарифмический декремент колебаний λ .
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно пропорциональная времени τ , по истечении которого амплитуда колебаний убывает в е раз. Для колебательного контура данная величина вычисляется по формуле: β = Rпотерь /(2L) .
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент равен коэффициенту затухания, умноженному на период колебаний: λ = βT .

С учётом коэффициента затухания формулы приобретают следующий вид:

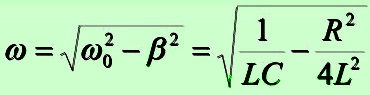
Заряд: q(t) = qmax cos(ωt) e (-βt) ;
Напряжение: U(t) = Umax cos(ωt) e (-βt) ;
Сила тока: I(t) = Imax sin(ωt) e (-βt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) ;
Период: ;
Круговая (циклическая) частота: ;

Добротность: Q = Lω/R .

При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие β 2 2 , круговая частота контура равна ω ≈ ω0 , а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.

Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.

Расчёт резонансной частоты, добротности и коэффициента
затухания контура

Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.

А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.

Чему равна максимальная сила тока, протекающего через колебательный контур с катушкой, имеющей индуктивность 6 мкГн и

Тема: Расчет максимальной силы тока в колебательном контуре

Объяснение:
Чтобы найти максимальную силу тока в колебательном контуре, используем формулу:

Пример использования:
Дано:
— Ф
— Гн

Решение:
Переводим значения в базовые единицы:
— Ф = 40 пФ = 40times10^ Ф.
— Гн = 6 мкГн = 6times10^ Гн.

Подставляем значения в формулу:
—

Схемы соединения катушек индуктивностей

Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:

Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:

Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.

Добротность катушки индуктивности

На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.

Добротность катушки индуктивности может быть найдена через следующую формулу:

где R является собственным сопротивлением обмотки.

Чему равна максимальная сила тока, протекающего через колебательный контур с катушкой, имеющей индуктивность 6 мкГн и

Тема: Расчет максимальной силы тока в колебательном контуре

Объяснение:
Чтобы найти максимальную силу тока в колебательном контуре, используем формулу:

Пример использования:
Дано:
— Ф
— Гн

Решение:
Переводим значения в базовые единицы:
— Ф = 40 пФ = 40times10^ Ф.
— Гн = 6 мкГн = 6times10^ Гн.

Подставляем значения в формулу:
—

Конструкция катушки индуктивности

Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.

Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.

Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.

Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.

Применение катушек индуктивности

Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.

Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.

Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.

Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.

Нет связанных сообщений