Какова связь между циклической частотой и периодом

Содержание

Обучайтесь и развивайтесь всесторонне вместе с нами, делитесь знаниями и накопленным опытом, расширяйте границы знаний и ваших умений.

поделиться знаниями или
запомнить страничку

Все категории
экономические 43,679
гуманитарные 33,657
юридические 17,917
школьный раздел 612,672
разное 16,911

Формулы для частных случаев нахождения циклической частоты

Пружинный маятник совершает гармонические колебания с циклической частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Гармонические колебания физического маятника происходят с циклической частотой равной:

где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.

Частным случаем физического маятника является математический маятник (физический маятник, масса которого сосредоточена в точке), циклическая частота его колебаний может быть найдена как:

где $l$ — длина подвеса, на которой находится материальная точка.

Частота колебаний в электрическом контуре равна:

где $C$ — емкость конденсатора, который входит в контур; $L$ — индуктивность катушки контура.

Если колебаний являются затухающими, то их частоту находят как:

где $delta $ — коэффициент затухания; в случае с затуханием колебаний, $<omega >_0$ называют собственной угловой частотой колебаний.

Примеры задач с решением

Задание. В электрический колебательный контур (рис.1) входит соленоид, длина которого $l$, площадь поперечного сечения $S_1$, число витков $N $и плоский конденсатор с расстоянием между пластинами $d$, площадью пластин $S_2$. Какова частота собственных колебаний контура ($<omega >_0$)?

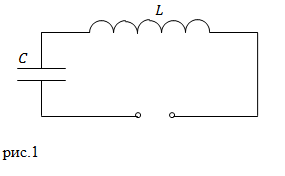
Урок 87 (осн). Вращательное движение. Период и частота вращения

Решение. Основой для решения задачи служить формула для частоты колебаний в электрическом контуре:

Элементом, обладающим индукцией в нашем контуре является соленоид. Индуктивность соленоида равна:

где $mu =1$, $<mu >_0$ — магнитная постоянная.

Емкость плоского конденсатора вычислим по формуле:

где $varepsilon =1$,

Формулы для частных случаев нахождения циклической частоты

Пружинный маятник совершает гармонические колебания с циклической частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Гармонические колебания физического маятника происходят с циклической частотой равной:

где $l$ — длина подвеса, на которой находится материальная точка.

Частота колебаний в электрическом контуре равна:

где $C$ — емкость конденсатора, который входит в контур; $L$ — индуктивность катушки контура.

Если колебаний являются затухающими, то их частоту находят как:

$ — электрическая постоянная.

Правые части выражений (1.2) и (1.3) подставим в (1.1) вместо соответствующих величин:

Задание. Чему равна циклическая частота гармонических колебаний материальной точки, если амплитуда скорости точки равна $>_=v_0$, амплитуда ее ускорения: $>_=a_0$? Начальная фаза колебаний равна нулю.

Решение. Из контекста условий задачи понятно, что колебания совершает координата $x$, поэтому уравнение колебаний (в общем виде) запишем как:

По условию задачи

Формулы для частных случаев нахождения циклической частоты

Пружинный маятник совершает гармонические колебания с циклической частотой равной:

$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.

Гармонические колебания физического маятника происходят с циклической частотой равной:

где $l$ — длина подвеса, на которой находится материальная точка.

Частота колебаний в электрическом контуре равна:

где $C$ — емкость конденсатора, который входит в контур; $L$ — индуктивность катушки контура.

Если колебаний являются затухающими, то их частоту находят как:

0$=0. Тогда уравнение для скорости изменения параметра $xleft(tright)$ имеет вид:

Из выражения (2.2) следует, что:

Уравнение для ускорения материальной точки, используя (2.2) запишем как:

Мы получили следующую систему из двух уравнений с двумя неизвестными:

Найдем отношение $frac$, получим:

Гармонические колебания

Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах ( Г ) . Связь с циклической частотой ω и периодом T выражается с помощью формулы:

ω = 2 π f = 2 π T .

Рисунок 2 . 1 . 2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки.

Рисунок 2 . 1 . 2 . Стробоскопическое изображение гармонических колебаний. Начальная фаза φ 0 = 0 . Интервал времени между последовательными положениями тела τ = T 12 .

На графике 2 . 1 . 3 . показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний x m , или периода Т (частоты f ), или начальной фазы φ 0 .

Рисунок 2 . 1 . 3 . Во всех трех случаях для синих кривых φ 0 = 0 : a – красная кривая отличается от синей только большей амплитудой ( x ‘ m > x m ) ; b – красная кривая отличается от синей только значением периода ( T ‘ = T 2 ) ; с – красная кривая отличается от синей только значением начальной фазы φ 0 ‘ = — π 2 р а д .

Гармонический закон

Если колебания совершаются вдоль прямой О х , тогда направление вектора скорости аналогично. Определение скорости движения тела υ = υ x определяют из выражения υ = ∆ x ∆ t ; ∆ t → 0 .

Отношение ∆ x ∆ t при ∆ t → 0 математика трактует как вычисление производной функции x ( t ) за определенное время t . Обозначение принимает вид d x ( t ) d t , x ‘ ( t ) или x ˙ .

Гармонический закон движения записывается в качестве x = x m cos ( ω t + φ 0 ) . После вычисления производной формула приобретает вид:

υ = x ˙ ( t ) = — ω x m sin ( ω t + φ 0 ) = ω x m cos ω t + φ 0 + π 2 .

Слагаемое + π 2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ = ω x m производится при прохождении тела через положение равновесия, то есть x = 0 . Аналогично определяют ускорение a = a x . Тогда a = ∆ υ ∆ t , ∆ t → 0 . Отсюда следует, что a равняется производной функции υ ( t ) за время t или второй производной функции x ( t ) . Подставив выражения, получим

a = υ ˙ ( t ) = x ¨ ( t ) = — ω 2 x m cos ( ω t + φ 0 ) = — ω 2 x ( t ) .

Наличие отрицательного знака указывает на то, что ускорение a ( t ) имеет противоположный смещению x ( t ) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия x = 0 .

На рисунке 2 . 1 . 4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания.

Рисунок 2 . 1 . 4 . Графики координаты x ( t ) , скорости υ ( t ) и ускорения a ( t ) тела, совершающего гармонические колебания.

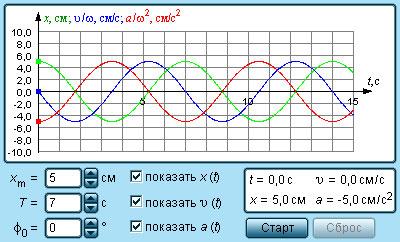
Рисунок 2 . 1 . 5 . Модель гармонических колебаний.

Связь линейной и циклической частоты. Связь периода гармонических колебаний с циклической частотой.

Гармоническимиколебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Период колебаний- наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние, в котором он находился в первоначальный момент, выбранный произвольно) Циклическая частота характеризует скорость изменения Фаза колебаний- это величина, которая определяет положение колебательной системы в любой момент времени Линейнаячастота — это скалярная физическая величина равная числу колебаний совершаемых системой за единицу времени, измеряется в Герцах .

Центр масс-воображаемая точка C,положение котрой характеризует распределение массы этой системы. Ее радиус-вектор равен 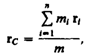где mi и ri — соответственно масса и радиус-вектор i-й материальной точки; n — число материальных точек в системе; – масса системы Закон сохранения импульсов: В замкнутой системе тел векторная сумма импульсов тел не изменяется при взаимодействии тел. Если импульс одного тела увеличился, то это означает, что у какого-то другого тела (или нескольких тел) в этот момент импульс уменьшился ровно на такую же величину. Закон сохранения импульса — Векторная сумма импульсов двух тел до взаимодействия равна векторной сумме их импульсов после взаимодействия 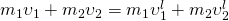Докажем закон сохранения импульса. Возьмем и обозначим массы двух тел и и скорости до взаимодействия , а после взаимодействия (столкновения) По третьему закон Ньютона силы, действующие на тела при их взаимодействии, равны по модулю и противоположны по направлению; поэтому их можно обозначить Для изменений импульсов тел при их взаимодействии на основании . Импульса силы можно записать так Для первого тела: Для второго тела: И тогда у нас получается, что закон сохранения импульсов выглядит так: Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих между собой тел при отсутствии действия сил со стороны других тел, не входящих в систему, или равны нулю, сумма импульсов тел остается неизменной. Необходимым условием применимости закона сохранения импульса к системе взаимодействующих тел является использование инерциальной системы отсчета В Формуле мы использовали : — Время взаимодействия тел — Импульс 1 тела до взаимодействия — Импульс 2 тела до взаимодействия 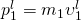— Импульс 1 тела после взаимодействия — Импульс 2 тела после взаимодействия Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.Реактивно движение оснвоано на принципе отдачи. В ракете при сгорании топлива газы, нагретые до высокой температуры, выбрасываются из сопла с большой скоростью относительно ракеты. Обозначим массу выброшенных газов через m, а массу ракеты после истечения газов через M. Тогда для замкнутой системы «ракета + газы» на основании закона сохранения импульса (по аналогии с задачей о выстреле из орудия) можно записать:

где V – скорость ракеты после истечения газов. В данном случае предполагается, что начальная скорость ракеты равнялась нулю. Полученная формула для скорости ракеты справедлива лишь при условии, что вся масса сгоревшего топлива выбрасывается из ракеты одновременно. На самом деле истечение происходит постепенно в течение всего времени ускоренного движения ракеты. Каждая последующая порция газа выбрасывается из ракеты, которая уже приобрела некоторую скорость.

Длина волны, частота волны, волновое число. Связь между скоростью волны ее длиной и частотой.

ЧАСТОТАВОЛНЫ, число полных колебаний или циклов волны, совершенных в единицу времени; если за 1 секунду, то измеряется в ГЕРЦАХ Волновое число -это отношение 2π радиан к длине волны (числоволн на длине 2π)

Закон равноускоренного движения по прямой, графики зависимости пути и скорости от времени при равноускоренном движении.

равноускоренным движением называют такое движение, при котором вектор ускорения остается неизменным по модулю и направлению. Так как υ – υ0 = at, окончательная формула для перемещения s тела при равномерно ускоренном движении на промежутке времени от 0 до t запишется в виде:

Для нахождения координаты y тела в любой момент времени t нужно к начальной координате y0 прибавить перемещение за время t:

Это выражение называют законом равноускоренного движения.

Логарифмический декремент затухания, связь с временем релаксации и периодом колебаний.

Логарифмический декремент затухания равен логарифму D: , N – число колебаний, совершаемых за время уменьшения амплитуды в e раз. Логарифмический декремент затухания обратно пропорционален числу колебаний, в результате которых амплитуда колебаний уменьшилась в ераз. Если А(t) и А(t+ Т) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение называется декрементом затухания.

Кинетическая энергия системы материальных точек (определение, единицы измерения). Связь между приращением кинетической энергии и работой сил, приложенных к телу

Механика Читать 0 мин.

Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.

Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.

Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac$ , где

Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где

N ― количество колебаний;

Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac<2pi>$ , где

ω ― циклическая частота [рад/с];

Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:

ω ― циклическая частота [рад/с];

φ0 ― начальная фаза колебаний, [рад];

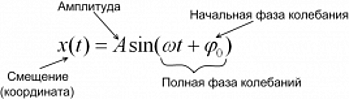
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.

Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.

Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.

Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где

φ ― полная фаза колебаний [рад];

φ0 ― начальная фаза колебаний, [рад];

ω ― циклическая частота [рад/с];

Пример анализа гармонических колебаний точки

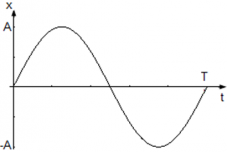
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где

ω ― циклическая частота [рад/с].

Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac<pi> +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac<3pi> +2pi n$ , где n = 0, 1 , 2, … N.

График колебания координаты точки имеет вид:

Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt’, где

v ― скорость движения точки [м/с];

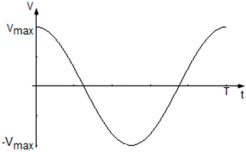
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt’ = |Asin(ωt)|’t = Acos(ωt).

Уравнение скорости точки равно v(t) = Acos(ωt), где

v ― скорость движения точки [м/с];

ω ― циклическая частота [рад/с];

Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.

График колебания скорости точки имеет вид:

Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.

Ускорение ― это производная скорости по времени: a = vt’, где

a ― ускорение движения точки [м/с2];

v ― скорость движения точки [м/с];

Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt’ = [Aωcos(ωt)]t’ = –Aω2sin(ωt).

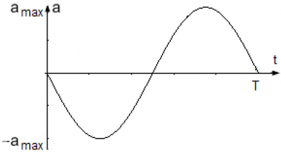
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где

a ― ускорение движения точки [м/с2];

ω ― циклическая частота [рад/с];

Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.

График колебания ускорения точки имеет вид:

Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где

E ― полная механическая энергия системы, E = const, [Дж];

EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];

EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].

Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).

Потенциальная энергия деформированной пружины равна EП = $frac$ , где

EП ― потенциальная энергия деформированной пружины, [Дж];

k ― коэффициент упругости пружины [Н/м];

x ― деформация пружины (величина ее удлинения или сжатия) [м].

У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac$ = $frac$ = $frac cdot A^2 sin^2 (omega t)$ .

Уравнение потенциальной энергии пружинного маятника EП = $frac cdot A^2 sin^2 (omega t)$ , где

EП ― потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

ω ― циклическая частота [рад/с];

Амплитуда потенциальной энергии пружинного маятника равна EПmax = $fracA^2$ , где

EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];

k ― коэффициент упругости пружины [Н/м];

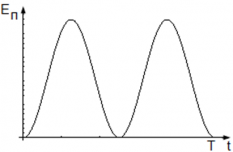
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.

График колебаний потенциальной энергии пружинного маятника:

Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac$ , где

Eк ― кинетическая энергия тела, [Дж];

v ― скорость движения тела, [м/с].

У тела, которое совершает колебательные движения, скорость ― переменная величина.

Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac$ = $frac cdot (Aomegacos(omega t))^2$ = $frac cdot A^2 omega^2 cos^2 (omega t)$ .

Уравнение кинетической энергии маятника Eк = $frac cdot A^2 omega^2 cos^2 (omega t)$ , где

Eк ― кинетическая энергия маятника, [Дж];

ω ― циклическая частота [рад/с];

Амплитуда кинетической энергии маятника равна EКmax = $frac cdot A^2 omega^2$ , где

EКmax ― максимальная кинетическая энергия маятника, [Дж];

ω ― циклическая частота [рад/с].

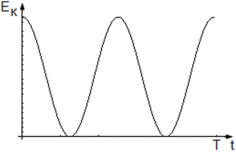
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.

График колебаний кинетической энергии маятника:

Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.

Период колебаний математического маятника равен T = $2pi sqrt>$ , где

l ― длина нити математического маятника [м];

g ― ускорение свободного падения [м/с2].

Период колебаний пружинного маятника равен T = $2pi sqrt>$ , где

Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.

Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.

На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.

Превращение энергии при гармонических колебаниях

Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

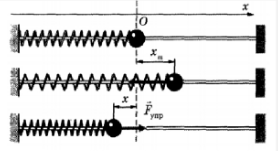
Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние xmax, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

W p m a x = k x 2 m a x 2 . .

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

W k m a x = m v 2 m a x 2 . .

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

W = W p + W k = k x 2 x 2 . . + m v 2 x 2 . . = k x 2 m a x 2 . . = m v 2 m a x 2 . .

В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

W p = k x 2 2 . . = k ( x m a x 2 . . ) 2 2 . . = k x 2 m a x 8 . .

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

W = W p m a x = k x 2 m a x 2 . .

Тогда кинетическая энергия равна:

W k = k x 2 m a x 2 . . − k x 2 m a x 8 . .

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

W k W p . . = k x 2 m a x 2 . . − k x 2 m a x 8 . . k x 2 m a x 8 . . . . = k x 2 m a x 2 . . 8 k x 2 m a x . . − 1 = 4 − 1 = 3

Резонанс

Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.

Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.

Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.

Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

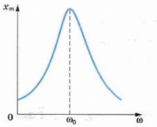
Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.

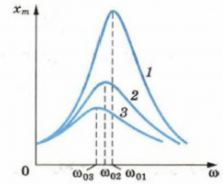
На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.

Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?

Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:

v = s t . . = 8 1 , 5 . . ≈ 5 , 33 ( м с . . ) ≈ 19 , 2 ( к м ч . . )

Текст: Алиса Никитина, 9.9k

Задание EF17508

Смещение груза пружинного маятника меняется с течением времени по закону x = A cos . 2 π T . . t , где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?

Алгоритм решения

1. Определить исходное значение потенциальной энергии шарика.
2. Сделать рисунок и определить положение шарика в начальный момент времени.

3. Определить положение шарика в момент в момент времени, когда потенциальная энергия шарика снова примет исходное значение.

4. Определить, через какое время шарик примет такое положение.

Решение

Известно, что смещение маятника меняется по закону:

x = A cos . 2 π T . . t

В начальный момент времени t = 0 смещение будет равно амплитуде, поскольку косинус нуля равен «1». Следовательно, исходное значение потенциальной энергии маятника равно:

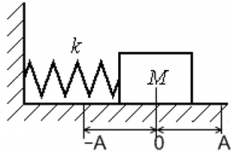
Сделаем рисунок, обозначив за x 0 положение равновесия системы. Тогда A и –A будут амплитудами (максимальными смещениями от положения равновесия).

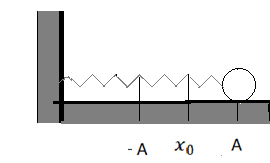
Потенциальная энергия зависит только от модуля смещения, поэтому ее значение станет таким же, как в начальный момент времени, когда смещение достигнет максимального смещения с противоположной стороны (оно составит –A). В этом легко убедиться:

W p t = k ( − A ) 2 2 . . = k A 2 2 . . = W p 0

К этому моменту пройдет половина периода колебания, следовательно:

t = T 2 . . = 1 2 . . = 0 , 5 ( с )

Задание EF17644

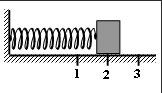
Груз изображённого на рисунке пружинного маятника совершает гармонические колебания между точками 1 и 3. Как меняются кинетическая энергия груза маятника, потенциальная энергия и жёсткость пружины при движении груза маятника от точки 2 к точке 3? Для каждой величины определите соответствующий характер её изменения:

1)	увеличивается
2)	уменьшается
3)	не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Вспомнить, от чего зависит кинетическая энергия груза маятника, и установить, как она меняется при движении груза маятника от точки 2 к точке 3.

2. Вспомнить, от чего зависит потенциальная энергия пружины маятника, и установить, как она меняется в рассматриваемый промежуток времени.

3. Вспомнить, от чего зависит жёсткость пружины, и установить, как она меняется.

Решение

Точка 2 соответствует положению равновесия, тока 3 — максимальному смещению пружинного маятника. Кинетическая энергия груза маятника зависит от скорости его перемещения:

Кинетическая энергия пружинного маятника максимально в положении равновесия и минимальная при максимальном смещении груза. Следовательно, на промежутке 2–3 она уменьшается.

Потенциальная энергия пружины маятника определяется формулой:

Так как смещение во время перемещения из точки 2 в точку 3 растет, то потенциальная энергия пружины маятника увеличивается.

Жесткость пружины зависит от природы материала. Это постоянная величина, которая с течением времени не изменяется.

Задание EF22760

Необходимо сделать нитяной маятник и с его помощью экспериментально определить ускорение свободного падения. Для этого школьник уже взял штатив с муфтой и лапкой, линейку и нить. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?

г) электронные весы

д) алюминиевый шарик

Алгоритм решения

1. Записать формулу, которая связывает ускорение свободного падения с периодом колебаний маятника.
2. Определить, что не хватает для проведения эксперимента и выбрать недостающие предметы из списка.

Решение

Ускорение свободного падения с периодом колебаний маятника связывает формула:

Следовательно, нужно значит не только длину нити маятника, но и период колебаний. Измерить его можно с помощью секундомера. А чтобы получить сам маятник, к нити нужно будет привязать массивный шарик. Например, алюминиевый.

Что такое разность фаз

Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.

Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.

( large varphi_) – для первого процесса и,

( large varphi_) – для второго процесса.

Рис. 12. Для двух колебаний можно ввести понятие разности фаз

Определим разность фаз между первым и вторым колебательными процессами:

Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.

Как связаны характеристики колебаний — формулы

Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.

Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.

Связь между периодом, количеством колебаний и общим временем колебательного процесса:

( large T left( c right) ) – время одного полного колебания (период колебаний);

( large N left( text right) ) – количество полных колебаний;

( large t left( c right) ) – общее время для нескольких колебаний;

Период и частота колебаний связаны так:

(large nu left( text right) ) – частота колебаний.

Количество и частота колебаний связаны формулой:

Связь между частотой и циклической частотой колебаний:

(large displaystyle omega left( frac> right) ) – циклическая (круговая) частота колебаний.

Фаза и циклическая частота колебаний связаны так:

(large varphi_ left( text right) ) — начальная фаза;

(large varphi left( text right) ) – фаза (угол) в выбранный момент времени t;

Между фазой и количеством колебаний связь описана так:

Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:

(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.