Сервис автоматически переводит введенное число во все указанные системы. При желании, ненужные системы можно отключить, сняв флажок (галочку) с соответствующего значения.
Цифры и буквы используемые в разных системах счисления (СС):
- двоичная: 0 и 1;
- восьмеричная: 0, 1, 2, 3, 4, 5, 6, 7;
- десятичная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
- шестнадцатеричная: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и букв: A, B, C, D, E, F;
- двоично-десятичная: 0 и 1.
Перевод из двоичной системы в восьмеричную и обратно
Разбиваем двоичное число на группы по 3 цифры, а затем находим соответствующее восьмеричное значение для каждой группы в таблице.
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример. Переведем двоичное число 1110101 в восьмеричную. Для начала разделим его на группы по 3 цифры, предварительно дописав нули с левой стороны числа, для того чтобы количество цифр стало кратно 3: 001 110 101. Находим соответствие каждой группе в таблице и получаем для первой группы — 1, для второй группы — 6, для третей группы — 5. Получаем конечный результат — 165.
Для перевода из восьмеричной системы в двоичную необходимо выполнить все действия в обратном порядке.
Пример. Переведем восьмеричное число 1374 в двоичное. Для этого найдем каждому восьмеричному значению соответствующее двоичное, воспользовавшись таблицей. Символу 1 соответствует 001, символу 3 — 011, символу 7 — 111, символу 4 — 100. Запишем полученные результаты в таком же порядке и получим: 001 011 111 100. Так как нули с левой стороны числа не имеют значения их можно не записывать: 1011111100.
Как перевести число из двоичной системы счисления
Чтобы перевести число из двоичной системы счисления в четвертичную, восьмеричную или шестнадцатеричную систему, нужно воспользоваться алгоритмом перевода:
- Разбить двоичное число справа налево на группы по 2 (для четвертичной СС), 3 (для восьмеричной СС) или 4 (для шестнадцатеричной СС) цифры. Если слева не будет хватать цифр для полной группы, нужно дописать необходимое количество незначащих нулей.
- Заменить каждую группу цифр на ее аналог в соответствующей системе счисления.
Перевести число 1111001102 из двоичной системы в четвертичную.
Разбиваем число на группы по 2 цифры справа налево и заменяем каждую группу на аналог в четвертичной системе счисления из таблицы:
1111001102 = 01 11 10 01 10 = 132124
Перевести число 1111001102 из двоичной системы в восьмеричную.
Как перевести из двоичной системы счисления в шестнадцатеричную
Разбиваем число на группы по 3 цифры справа налево и заменяем каждую группу на аналог в восьмеричной системе счисления из таблицы:
1111001102 = 111 100 110 = 7468
Перевести число 1111001102 из двоичной системы в шестнадцатеричную.
Разбиваем число на группы по 4 цифры справа налево и заменяем каждую группу на аналог в шестнадцатеричной системе счисления из таблицы:
1111001102 = 0001 1110 0110 = 1E616
Как перевести число в двоичную систему счисления
Чтобы перевести число из четвертичной, восьмеричной или шестнадцатеричной системы счисления в двоичную, нужно воспользоваться алгоритмом перевода:
- Заменить каждую цифру на двоичный аналог, состоящий из 2 (для четвертичной), 3 (для восьмеричной) или 4 (для шестнадцатеричной) цифр. Если нужно, число дополняется нулями слева.
- Вычеркнуть из числа незначащие нули.
Перевести число 1203234 из четвертичной системы в двоичную.
Выполняем замену каждой цифры на группу из 2 цифр в двоичной системе счисления:
1203234 = 01 10 00 11 10 11 = 110001110112
Перевести число 264750308 из восьмеричной системы в двоичную.
Выполняем замену каждой цифры на группу из 3 цифр в двоичной системе счисления:
264750308 = 010 110 100 111 101 000 011 000 = 101101001111010000110002
Перевести число 2AC0F7416 из шестнадцатеричной системы в двоичную.
Выполняем замену каждой цифры на группу из 4 цифр в двоичной системе счисления:
2AC0F7416 = 0010 1010 1100 0000 1111 0111 0100 = 101010110000001111011101002
Поделитесь статьей с одноклассниками «Как перевести из двоичной в восьмеричную, шестнадцатеричную и четвертичную системы».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Перевод числа из двоичной системы счисления в шестнадцатеричную
Преобразование числа из двоичной системы, основанной на двух цифрах (0 и 1), в шестнадцатеричную систему, где используются цифры от 0 до 9 и буквы от A до F, требует группировки битов и их последующего представления в виде шестнадцатеричных символов.
Методика перевода из двоичной системы в шестнадцатеричную
- Группировка битов Для начала необходимо разделить число на разряды. Каждая цифра в двоичном числе представляет собой умножение числа 2 в степени, соответствующей позиции разряда, начиная справа налево. Например, для числа 11011010: Группируем биты: 1101 1010
- Преобразование в шестнадцатеричную систему Каждую группу из четырех битов преобразуем в соответствующий шестнадцатеричный символ. Например, для числа 1101 1010: Каждая группа преобразуется в шестнадцатеричный символ: DA Итоговое шестнадцатеричное число: DA
Пример на Python
Приведем пример простой функции на языке Python для перевода числа из двоичной системы в шестнадцатеричную систему:
def binary_to_hex(binary_number): hexadecimal_digits = «0123456789ABCDEF» hex_number = «» # Добавляем нули слева, если количество битов не кратно четырем while len(binary_number) % 4 != 0: binary_number = «0» + binary_number # Группируем биты и преобразуем их в шестнадцатеричные символы for i in range(0, len(binary_number), 4): bits = binary_number[i:i+4] decimal_value = int(bits, 2) hex_digit = hexadecimal_digits[decimal_value] hex_number += hex_digit return hex_number # Пример использования binary_num = «11011010» hex_num = binary_to_hex(binary_num) print(f»Двоичное число в шестнадцатеричной системе = «)
Применение перевода в шестнадцатеричную систему
Перевод чисел из двоичной системы в шестнадцатеричную используется в информатике для удобства представления и записи больших двоичных чисел. Шестнадцатеричная система удобна для работы с данными и позволяет более компактно записывать большие двоичные значения.
Перевод из двоичной системы счисления в шестнадцатеричную
Вы делитесь ссылкой на ваш сохраненный расчет. Изменения, внесенные в расчет, будут автоматически доступны по ссылке.
Вы делитесь ссылкой на статичный расчет. При изменении вами расчета, изменения не будут транслироваться по ссылке.
Как перевести
Преобразовать число из двоичной системы счисления в шестнадцатеричную можно тремя способами.
Перевести сначала в десятичную систему счисления, затем из нее в конечную.
Разбиваем число на группы по 4 цифры справа налево. Последнюю (левую) группу дополним при необходимости ведущими нулями. Внутри каждой полученной группы произведем умножение каждой цифры на 2 n , где n — номер разряда , начиная с 0. Затем сложим результаты.
110102 = (0001) (1010) = (0*2 3 + 0*2 2 + 0*2 1 + 1*2 0 ) (1*2 3 + 0*2 2 + 1*2 1 + 0*2 0 ) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A16
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
1011111002 = (0001) (0111) (1100) = 17C16
Нужно знать, что такое двоичная или бинарная система счисления
Прежде чем размышлять о том, как перевести число из 2 в 16, необходимо хорошо понимать, что собою представляют числа в двоичной системе счисления. Напомню, что алфавит бинарной системы счисления состоит из двух допустимых элементов – 0 и 1. Это означает, что абсолютно любое число, записанное в двоичном виде, будет состоять из набора нулей и единиц. Вот примеры чисел, записанных в бинарном представлении: 10010, 100, 111101010110, 1000001.
С бинарной системой мы разобрались, вспомнили базовые моменты, сейчас поговорим о 16-ричной системе. Алфавит 16-ричной системы счисления состоит из шестнадцати различных знаков: 10 арабских цифр (от 0 до 9) и 6 первых заглавных латинских букв (от ‘А’ до ‘F’). Это означает, что абсолютно любое число, записанное в шестнадцатеричном виде, будет состоять из знаков вышеприведенного алфавита. Вот примеры чисел, записанных в 16-ричном представлении:
| 810A | FCDF | 198303 | 100FFF0 |
Поговорим об алгоритме преобразования числа из 2-ной в 16-ричную систему счисления
Нам потребуется в обязательном порядке рассмотреть кодировочную таблицу Тетрад. Без применения данной таблицы будет довольно затруднительно оперативно осуществлять перевод чисел из 2 в 16 систему.
Назначение кодировочной таблицы Тетрад: однозначно сопоставить символы двоичной системы счисления и 16-ричной системы счисления.
Таблица Тетрад имеет следующую структуру:
Таблица Тетрад
0000 — 0
0001 — 1
0010 — 2
0011 — 3
0100 — 4
0101 — 5
0110 — 6
0111 — 7
1000 — 8
1001 — 9
1010 — A
1011 — B
1100 — C
1101 — D
1110 — E
1111 — F
Допустим нам требуется преобразовать число 1010111110010102 в 16-ричную систему. В первую очередь необходимо исходный бинарный код разбить на группы по четыре разряда, причем, что очень важно, разбиение в обязательном порядке следует начинать справа налево.
101 . 0111 . 1100 . 1010
После разбиения мы получили четыре группы: 101, 0111, 1100 и 1010. Особого внимания требует самый левый сегмент, то есть сегмент 101. Как видно, его длина составляет 3 разряда, а необходимо, чтобы его длина равнялась четырем, следовательно, дополним данный сегмент ведущим незначащим нулем:
101 -> 0 101.
Вы скажите, а собственно на каком основании мы дописываем слева от числа какой-то 0? Все дело в том, что добавление незначащих нулей не оказывает никакого влияния на значение исходного числа. Следовательно, мы имеем полное право дописать слева от бинарного числа не только один ноль, а в принципе любое количество нулей и получить число нужной длины.
На заключительном этапе преобразования необходимо каждую из полученных бинарных групп перевести в соответствующее значение по кодировочной таблице Тетрад.
| 0101 -> 5 | 0111 -> 7 | 1100 -> C | 1010 -> A |
А сейчас я вам предлагаю ознакомиться с мультимединым решением, в котором показано как неравномерный код преобразуется из бинарного состояния в 16-ричное состояние:
Преобразуйте каждые 4 двоичные цифры в шестнадцатеричную в соответствии с этой таблицей:
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | А |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Преобразуйте (01001110) 2 в шестнадцатеричное:
Правила перевода чисел из двоичной системы счисления в другую
- Чтобы перевести число из двоичной системы счисления в восьмеричную, его необходимо разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, затем каждую триаду заменить соответствующей восьмеричной цифрой согласно таблице 4.
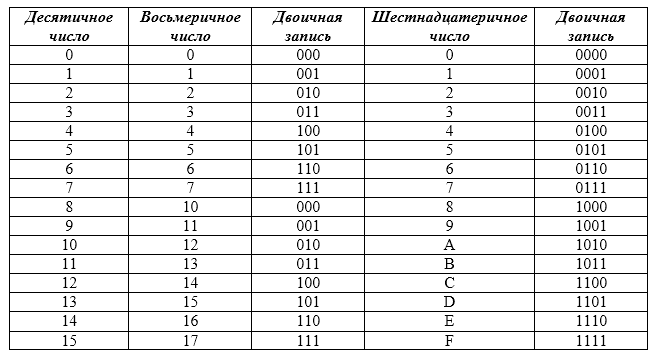
Рисунок 7. Таблица 4
Число $1001011_2$ перевести в восьмеричную систему счисления.
Решение. Используя таблицу 4, переведем число из двоичной системы счисления в восьмеричную:
$001 001 011_2 = 113_8$
- Чтобы перевести число из двоичной системы счисления в шестнадцатеричную, его следует разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, затем каждую тетраду заменить соответствующей восьмеричной цифрой согласно таблице 4.
Число $1011100011_2$ перевести в шестнадцатеричную систему счисления.
Решение. Используя таблицу 4 переведем число из двоичной системы счисления в шестнадцатеричную:
$0010 1110 0011_2 = 2E3_$
Правила перевода чисел из любой системы счисления в двоичную
- Для перевода числа из восьмеричной системы счисления в двоичную следует каждую цифру заменить эквивалентной ей двоичной триадой, представленной в таблице 4.
Число $531_8$ перевести в двоичную систему счисления. Решение: $531_8 = 101011001_2$
- Для перевода числа из шестнадцатеричной системы счисления в двоичную требуется каждую цифру заменить эквивалентной ей двоичной тетрадой, представленной в таблице 4.
Число $EE8_$ перевести в двоичную систему счисления.
Решение:
- При переводе числа из восьмеричной системы счисления в шестнадцатеричную и обратно, необходимо выполнить промежуточный перевод чисел в двоичную систему.
Число $FEA_$ перевести в восьмеричную систему счисления.
Решение:
$111 111 101 010_2 = 7752_8$
Число $6635_8$ перевести в шестнадцатеричную систему счисления.
Решение:
$1101 1001 11012 = D9D_$




