Как переводить числа в шестнадцатеричную систему счисления

Представлено правило перевода двоичного числа в восьмеричную и шестнадцатеричную системы счисления.

Система счисления – это способ наименования и представления чисел с помощью символов. Такие символы в любой системе счисления называются цифрами.

Алфавит системы счисления – это совокупность символов, используемых в данной системе счисления.

Все системы счисления подразделяются на два класса – позиционные и непозиционные. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно P, то система счисления называется P-ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.

Запись произвольного числа x в P -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена

x = a n P n + a n -1 P n -1 + . + a 1 P 1 + a 0 P 0 + a -1 P -1 + . + a -m P -m

Двоичная система счисления – это система, в которой для записи чисел используются две цифры 0 и 1. Основанием двоичной системы счисления является число 2.

Двоичный код числа — запись этого числа в двоичной системе счисления. Например,

0=0 2
1=1 2
2=10 2
3=11 2 …
7=111 2
120=1111000 2 .

В восьмеричной системе используется восемь цифр: 0, 1, 2, 3, 4, 5, 6, 7. Эта система счисления используется как вспомогательная для записи информации в сокращенном виде. Для представления одной цифры восьмеричной системы используются три двоичных разряда (триада):

Правило записи

Наименование системы счисления	Запись
Двоичная	1012
Восьмеричная	7028
Десятичная	19010 (если основание у числа не указано, то считается что число записано в десятичной системе)
Шестнадцатеричная	A1F16

Основание системы счисления указывает на количество символов алфавита используемой системы счисления.

Десятичная система счисления

Десятичная система счисления — это позиционная система (т.е. значение каждой цифры в записи числа зависит от его разряда) по основанию 10.

В приведенном выше числе три разряда: единицы, десятки и сотни. Можем прочитать это число так 1 сотня, 2 десятки и 3 единицы (100 + 20 + 3).

Перевод чисел из десятичной в шестнадцатеричную систему счисления. Лекция по информатике №3

Каждый разряд мы можем пронумеровать, с младшего (единицы), начиная с ноля.

Индекс разряда	2	1	0
Число	1	2	3

После того, как индексы расставлены, можно записать число в развернутой форме. Развернутая форма записывается в виде суммы разрядных слагаемых. Каждое разрядное слагаемое записывается в виде числа умноженного на основание системы возведенное в степень индекса(веса) разряда.

1*10 2 + 2*10 1 + 3*10 0 = 100 + 20 + 3

Перевод из десятичной системы счисления в шестнадцатеричную

Вы делитесь ссылкой на ваш сохраненный расчет. Изменения, внесенные в расчет, будут автоматически доступны по ссылке.

Вы делитесь ссылкой на статичный расчет. При изменении вами расчета, изменения не будут транслироваться по ссылке.

Как перевести

Для того, чтобы преобразовать число из десятичной системы счисления в шестнадцатеричную, необходимо выполнить следующие действия.

1. Делим десятичное число на 16 и записываем остаток от деления.
2. Результат деления вновь делим на 16 и опять записываем остаток.
3. Повторяем операцию до тех пор пока результат деления не будет равен нулю.
4. Запишем полученные остатки в обратном порядке и получим искомое число.

В шестнадцатеричной записи числа 10, 11, 12, 13, 14, 15 записываются буквами A, B, C, D, E, F соответственно.

Переведем число 100010 в шестнадцатеричную систему:

1000 / 16 = 62 (остаток 8)
62 / 16 = 3 (остаток 14, в шестнадцатеричной системе – E)
3 / 16 = 0 (остаток 3)
Записываем остатки в обратном порядке, получаем результат: 3E816

2. Перевод чисел в системах счисления

Рассмотрим алгоритмы перевода чисел из одной позиционной системы в другую систему счисления. В подразделе рассмотрены алгоритмы перевода чисел в десятичную систему счисления из произвольной системы счисления, а также перевод чисел из произвольной системы счисления в десятичную систему счисления.

Для перевода двоичного числа в восьмеричную (шестнадцатеричную) систему счисления необходимо исходное двоичное число разбить на триады (тетрады). Триада (тетрада) – это последовательность трех (четырех) соседних двоичных цифр исходного числа. Разделение на триады (тетрады) проводится от разделительной точки. Целая часть числа разбивается при движении от разделительной точки влево. Дробная часть числа разбивается при движении от разделительной точки вправо. Если крайние группы цифр, полученные после разбиения, не содержат три (четыре) цифры, то они дополняются нулями. Крайняя левая группа – нулями слева, крайняя правая группа – нулями справа. Затем каждой триаде (тетраде) необходимо поставить в соответствие восьмеричную (шестнадцатеричную) цифру, используя табл. 2.1. Искомое число – последовательность восьмеричных (шестнадцатеричных) цифр, записанных в том же самом порядке, в каком располагаются соответствующие триады (тетрады) в записи исходного числа.

Пример 5.1. Дано двоичное число N2 = 11101.012. Выполним перевод числа в восьмеричную систему счисления.

1. Разобьем целую и дробную части числа на триады и дополним крайние группы цифр нулями:

2. Поставим в соответствие каждой триаде восьмеричную цифру:

Таким образом, в восьмеричной системе счисления число 11101.012 имеет вид:

Пример 5.2. Дано двоичное число N2 = 11101.012. Выполним перевод числа в шестнадцатеричную систему счисления.

1. Разобьем целую и дробную части числа на тетрады и дополним крайние группы цифр нулями:

11101→ 0001 1101;

2. Поставим в соответствие каждой тетраде шестнадцатеричную цифру:

Таким образом, в шестнадцатеричной системе счисления число 11101.012 имеет вид:

2.2. Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления

Для перевода чисел из восьмеричной (шестнадцатеричной) системы счисления в двоичную систему счисления необходимо каждой восьмеричной (шестнадцатеричной) цифре исходного числа поставить в соответствие триаду (тетраду) двоичных цифр. Запись искомого числа является последовательностью полученных триад (тетрад), расположенных в том же самом порядке, в котором располагаются соответствующие восьмеричные (шестнадцатеричные) цифры в записи исходного числа.

Пример 5.3. Дано восьмеричное число N8 = 273.57. Выполнить перевод числа в двоичную систему счисления.

Заменим каждую цифру числа на соответствующую триаду:

Тогда в двоичной системе счисления число имеет вид:

N2 = 10111011.101111.

Пример 5.4. Дано шестнадцатеричное число N16 = 273.5716. Выполним перевод числа в двоичную систему счисления.

Заменим цифру шестнадцатеричного числа соответствующей тетрадой:

Тогда в двоичной системе счисления число имеет вид:

N2 = 001001110011.01010111.

Правила перевода чисел из любой системы счисления в двоичную

• Для перевода числа из восьмеричной системы счисления в двоичную следует каждую цифру заменить эквивалентной ей двоичной триадой, представленной в таблице 4.

Число $531_8$ перевести в двоичную систему счисления. Решение: $531_8 = 101011001_2$

• Для перевода числа из шестнадцатеричной системы счисления в двоичную требуется каждую цифру заменить эквивалентной ей двоичной тетрадой, представленной в таблице 4.

Число $EE8_$ перевести в двоичную систему счисления.

Решение:

• При переводе числа из восьмеричной системы счисления в шестнадцатеричную и обратно, необходимо выполнить промежуточный перевод чисел в двоичную систему.

Число $FEA_$ перевести в восьмеричную систему счисления.

Решение:

$111 111 101 010_2 = 7752_8$

Число $6635_8$ перевести в шестнадцатеричную систему счисления.

Решение:

$1101 1001 11012 = D9D_$

Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения

Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:

число	6	3	7	2
позиция	3	2	1	0

Тогда число 6372 можно представить в следующем виде:

6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .

Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.

Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:

число	1	2	8	7	.	9	2	3
позиция	3	2	1	0	-1	-2	-3

Тогда число 1287.923 можно представить в виде:

1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .

В общем случае формулу можно представить в следующем виде:

Цn·s n +Цn-1·s n-1 +. +Ц1·s 1 +Ц0·s 0 +Д-1·s -1 +Д-2·s -2 +. +Д-k·s -k

где Цn-целое число в позиции n, Д-k- дробное число в позиции (-k), s — система счисления.

Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр , в восьмеричной системе счисления — из множества цифр , в двоичной системе счисления — из множества цифр , в шестнадцатеричной системе счисления — из множества цифр , где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.

В таблице Таб.1 представлены числа в разных системах счисления.

Таблица 1

Система счисления
10	2	8	16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Перевод чисел из одной системы счисления в другую

Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.

С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.

Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:

Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:

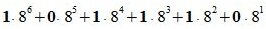
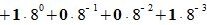
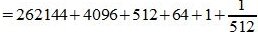
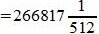
Пример 3. Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:

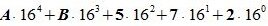
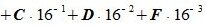
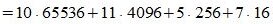
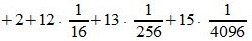
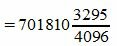
Здесь A -заменен на 10, B — на 11, C- на 12, F — на 15.

Перевод из двоично-десятичной системы в десятичную и обратно

Для этого необходимо разбить двоичное число на группы по 4 символа, предварительно дописав с левой стороны необходимое количество нулей, что бы общее количество символов стало кратно 4. Далее переводим каждую группу в десятичное значение и полученные результаты записываем в соответствующем порядке. Для упрощения задачи можно воспользоваться таблицей соответствия двоичного и десятичного значений.

значение2 значение10

0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9

Пример. Переведем число 111100100110001 из двоично-десятичной системы в десятичную. Для начала допишем недостающий ноль с левой стороны и разделим по 4 символа: 0111 1001 0011 0001. Далее находим соответствующие десятичные значения в таблице и получаем: 7931.

Для обратного перевода необходимо произвести все действия в обратном порядке, то есть каждой цифре десятичного значения находим по таблице соответствующее двоичное значение и записываем полученные результаты в таком же порядке, как и цифры десятичного числа.

Пример. Десятичное число 1234 переведем в двоично-десятичную. Находим по таблице все соответствия: символу 1 соответствует 0001, символу 2 — 0010, символу 3 — 0011 и символу 4 — 0100. В результате получаем: 0001001000110100.

Перевод из десятичной в двоичную, восьмеричную и шестнадцатеричную системы

Для того что бы перевести из десятичной системы в любую другую необходимо последовательно делить число на основание той системы в которую переводим до тех пор пока частное от деления не станет равным нулю. Далее записываем остатки от делений в обратном порядке. Полученная последовательность будет являться результатом перевода в выбранную систему счисления. Для понимания указанных действий разберем последовательное преобразование для каждой из систем.

Из десятичной в двоичную. Исходное число 230, основание системы «2». Производим последовательное деление:

• 230 ÷ 2 = 115 (в остатке 0);
• 115 ÷ 2 = 57 (в остатке 1);
• 57 ÷ 2 = 28 (в остатке 1);
• 28 ÷ 2 = 14 (в остатке 0);
• 14 ÷ 2 = 7 (в остатке 0);
• 7 ÷ 2 = 3 (в остатке 1);
• 3 ÷ 2 = 1 (в остатке 1);
• 1 ÷ 2 = 0 (в остатке 1).

Записываем остатки от деления на 2 в обратном порядке и получаем следующую последовательность: 11100110. Полученный результат является двоичным представлением числа 230.

Из десятичной в восьмеричную. Исходное число 789, основание системы «8». Производим последовательное деление:

• 789 ÷ 8 = 98 (в остатке 5);
• 98 ÷ 8 = 12 (в остатке 2);
• 12 ÷ 8 = 1 (в остатке 4);
• 1 ÷ 8 = 0 (в остатке 1).

Записываем остатки от деления на 8 в обратном порядке и получаем следующую последовательность: 1425. Полученный результат является восьмеричным представлением числа 789.

Из десятичной в шестнадцатеричную. Исходное число 7000, основание системы «16». Производим последовательное деление:

• 7000 ÷ 16 = 437 (в остатке 8);
• 437 ÷ 16 = 27 (в остатке 5);
• 27 ÷ 16 = 1 (в остатке 11);
• 1 ÷ 16 = 0 (в остатке 1).

Записываем остатки от деления на 16 в обратном порядке. Если остаток от деления больше 9, то вместо числа записываем букву, соответствие чисел и букв представлено ниже в таблице. В результате получаем следующую последовательность: 1B58. Полученный последовательность является шестнадцатеричным представлением числа 7000.

число буква

10	A
11	B
12	C
13	D
14	E
15	F