1. Цепь рис. 2.3 содержит шесть ветвей (), четыре узла (), один источник тока ().
Выберем положительные направления токов в схеме, как это указано на рис. 2.4.
2. Определим достаточное количество уравнений для расчета цепи по первому закону Кирхгофа:
по второму закону Кирхгофа:
Достаточное количество уравнений равно пяти, что соответствует числу неизвестных токов (рис. 2.4).
3. Составим систему уравнений по законам Кирхгофа.
Три уравнения по первому закону Кирхгофа, например, для узлов 2, 3 и 4. Два уравнения по второму закону Кирхгофа. Положительные направления обхода независимых контуров выберем в соответствии с указанными на рис. 2.4.
П р и м е ч а н и е: При выборе независимых контуров необходимо следить за тем, чтобы контур не содержал ветви с источником тока.
4. После подстановки числовых значений параметров элементов цепи получим:
5. Решение системы получим в матричной форме
6. В результате решения матричной системы уравнений находим токи:
Знак минус у тока означает, что действительное направление тока противоположно направлению, выбранному на схеме рис.2.4.
П р и м е ч а н и е: изменять знак тока на обратный не следует, так как это может привести к ошибке в дальнейших расчетах.
7. Правильность расчета установим путем проверки баланса мощностей. Мощность, поступающая в цепь от источников энергии должна равняться сумме мощностей потребителей электрической энергии:
Предварительно найдем напряжение на зажимах с источником тока (рис. 2.4). На основании второго закона Кирхгофа получим:
Полная мощность, развиваемая источниками энергии
Полная мощность потерь в резистивных сопротивлениях
Погрешность расчета составляет:
Для схемы электрической цепи (рис. 2.5) построить график изменения потенциала во внешнем контуре. Параметры элементов цепи заданы , , , , , , , .
Рис. 2.5. Рис. 2.6.
1. Предварительно выполним расчет токов внешнего контура. Цепь (рис. 2.5) содержит шесть ветвей (), четыре узла (), один источник тока ().
Выберем положительные направления токов в схеме цепи в соответствии с указанными на рис. 2.6.
2. Достаточное количество уравнений для расчета цепи по первому закону Кирхгофа , по второму закону Кирхгофа .
Общее количество уравнений равно пяти.
3. Три уравнения по первому закону Кирхгофа составим для узлов 1, 2 и 4.
Два уравнения по второму закону Кирхгофа для контуров и обозначенных в схеме на рис. 2.6.
4. Запишем систему в матричной форме
5. После подстановки числовых значений получим
6. Решение матричной системы позволяет определить токи
7. Выделим элемент внешнего контура (рис. 2.7). Примем потенциал точки 1 равным нулю (). Рассчитаем потенциалы точек контура, обходя его по часовой стрелке:
Олимпиадная задача по ТОЭ #4. Постоянный ток. Определить показание вольтметра
8. Порядок построения потенциальной диаграммы представлен на рис. 2.8. На диаграмме по оси абсцисс откладываем значения сопротивлений участков в последовательности расположения их в контуре.
Определить показания вольтметров в схеме цепи рис. 2.9, если , , , , , , . Внутреннее сопротивление вольтметров принять равным .
Рис. 2.9. Рис. 2.10.
1. Заменим вольтметры, изображенные на схеме (рис. 2.9), векторами напряжений, указывающих на разность потенциалов между точками их подключения (рис. 2.10). Направления действия векторов напряжений выбираем произвольно.
2. Определим недостающий ток по первому закону Кирхгофа
3. Показание вольтметра определим из выражения, записанного по второму закону Кирхгофа для замкнутого контура (рис. 2.10).
4. Показание вольтметра определим из выражения, записанного по второму закону Кирхгофа для замкнутого контура , рис. 2.10:
5. Показание вольтметра определим из выражения, записанного по второму закону Кирхгофа для замкнутого контура , рис. 2.10:
Определить показания приборов в схеме рис. 2.11, если , , , , . Внутренние сопротивления вольтметров принять , амперметров .
Рис. 2.11. Рис. 2.12.
1. Выполним замену приборов с учетом их внутренних сопротивлений (рис. 2.12) и обозначим токи ветвей.
2. Показание амперметра равно значению тока (рис. 2.12)
3. Показание амперметра будет определяться током источника , включенным последовательно в цепь с амперметром, т.е. .
4. Показание вольтметра определим из выражения, записанного по второму закону Кирхгофа для замкнутого контура (рис. 2.12):
5. Показание вольтметра определим по выражению, записанному по второму закону Кирхгофа для замкнутого контура (рис. 2.12):
Задачи для самостоятельного решения
Задача 2.6. В цепи (рис. 2.13) , , , . Определить показания приборов, если , .
Задача 2.7. Определить показание вольтметра в цепи рис. 2.14. Параметры цепи заданы: , , .
Рис. 2.13. Рис. 2.14.
Задача 2.8. Для схемы на рис. 2.15, пользуясь законами Кирхгофа, найти все токи, если , , , , , , .
Задача 2.9. Для схемы рис. 2.16, пользуясь законами Кирхгофа определить токи в ветвях с резистивными сопротивлениями, если , , , .
Рис. 2.15. Рис. 2.16.
Задача 2.10. Для схемы рис. 2.17, пользуясь законами Кирхгофа определить все токи, если , , , , , , , , .
Задача 2.11. Напряжение на входе цепи (рис. 2.18). составляет . Определить напряжение на выходе цепи, если , , , .
Рис. 2.17. Рис. 2.18.
Задача 2.12. Определить токи в схеме рис. 2.19, если , , , , , . Проверить баланс мощностей.
Задача 2.13. Для схемы рис. 2.20, пользуясь законами Кирхгофа определить показания приборов, если , , , , , . Принять внутренние сопротивления приборов: , .
Рис. 2.19. Рис. 2.20.
Задача 2.14. Для схемы рис. 2.21, пользуясь законами Кирхгофа определить все токи. Дано , , , , .
Задача 2.15. Рассчитать с использованием законов Кирхгофа токи в схеме рис.2.22, если , , , , , , .
Задача 2.16. Для схемы рис. 2.23, пользуясь законами Кирхгофа определить все токи, если , , , , , .
Рис. 2.21. Рис. 2.22.
Задача 2.17. Для схемы рис. 2.24, пользуясь законами Кирхгофа определить все токи. Дано , , , , , , , .
Рис. 2.23. Рис. 2.24.
Решение
Поскольку вольтметр имеет бесконечно большое сопротивление, он не оказывает влияние на величину тока рассматриваемой одноконтурной электрической цепи, и поэтому при определении величины тока не играет никакой роли и не учитывается.
Направление тока, как и направление обхода контура, выбирается произвольно (рис.1.1.17).
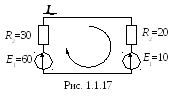
По второму закону Кирхгофа:
2. Определение показания вольтметра.
Показание вольтметра не зависит от того, какая часть схемы рассматривается с целью его определения.
Для определения показания вольтметра составляется уравнение, согласно II закону Кирхгофа (направления обхода контуров показаны на рис. 1.1.18, а и 1.1.18,б)
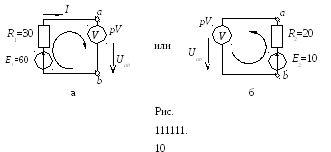
Е1 = R1 I + Uab , Uab = E1 – R1 I = 60 – 30 · 1 = 30, B
или Е2 = R2 I + Uab , Uab = E2 – R2 I = 10 – 20 · 1 = 30, B.
Вольтметр показывает значение, равное Vab, в рассматриваемом случае 30 В.
3.Определение режимов работы источников ЭДС.
Если мощность источника ЭДС P = I E – величина положительная, то источник работает в режиме генератора, в противном случае – в режиме приемника:
P1 = IE1 = 1· 60 = 60, Вт – источник ЭДС E1 в режиме генератора;
P2 = I E2 = 1· 10 = 10, Вт – источник ЭДС E2 в режиме приемника.
Задача 1.7. Рассчитать цепь методом контурных токов. Составить 
 баланс мощностей, используя.
баланс мощностей, используя.
1. Определение токов в ветвях.
Направление токов в ветвях и контурных токов (II IIII) выбираются произвольно, причем целесообразнее чтобы направления контурных токов совпадали с обходами соответствующих контуров (рис. 1.1.19).
Согласно методу контурных токов составляются уравнения ко II закону Кирхгофа для замкнутых независимых контуров цепи относительно не токов в ветвях, а контурных токов:
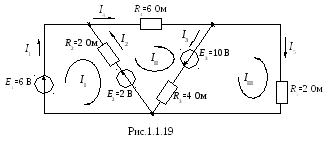
или 2II + 2 III ……………… = — 2 + 6;
2 II + (2 + 6 + 4)III – 4IIII = — 10 – 2;
откуда значения контурных токов:
II = 36/11 А, III = 14/11 А, IIII = 9/11 А
Токи во внешних ветвях:
I1 = II = 36/11 А, I4 = III = 14/11 А, I5 = IIII = 9/11 А,
а токи в смежных ветвях:
I2 = — II – III = — 36 / 11 + 14 / 11 = — 2, А,
I3 = IIII – III = 9 / 11 + 14 / 11 = 23 / 11, А.
2. Составление управления баланса мощности.
Алгебраическая сумма мощностей всех источников цепи равна арифметической сумме мощностей всех ее приемников:
или в числовом выражении
36/11·6 (-2) 2 + 23/11·10 = 2(-2) 2 + 4(23/11) 2 + 6(14/11) 2 + 2(9/11) 2 , Вт
402/11 = 402/11, Вт.
Задача 1.8. Определить токи в ветвях электрической цепи методом междуузлового напряжения (Ri, Ом, Ej, В) (рис. 1.1.20).
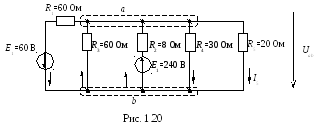
Решение
1. Определение междуузлового напряжения.
Потенциальные узлы отмечаются буквами с целью соблюдения знаков узловых токов, например, а u b, тогда искомое напряжение
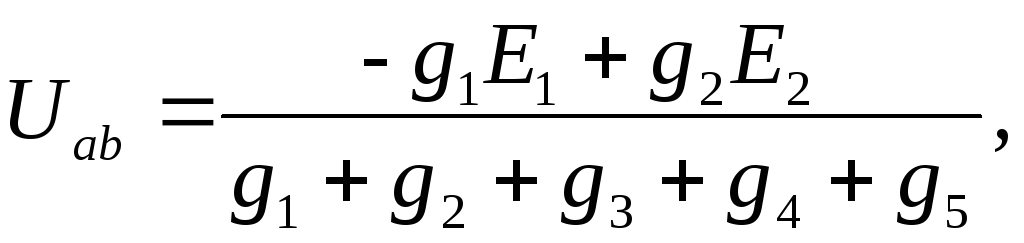

где gi = 1/Ri – проводимость i-ой ветви, См, или в числовом выражении
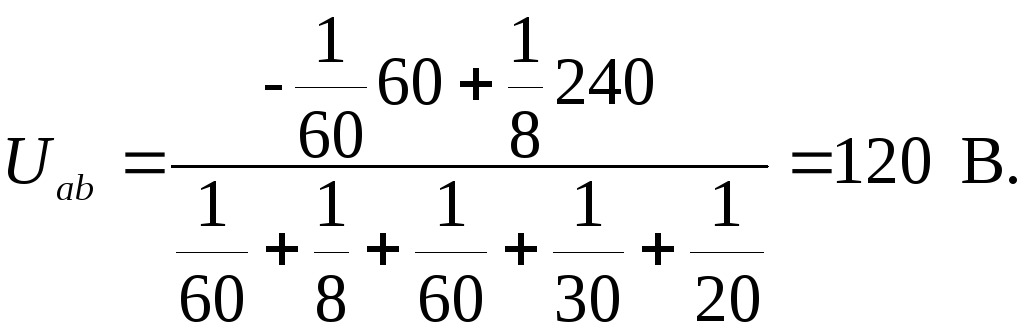
2. Определение токов в ветвях.
Направления токов в ветвях выбираются произвольно, а их величины определяются согласно закону Ома для активного или пассивного участков цепи:
I3 = — Uab/R3 = — 120/60 = -2 A;
I4 = Uab/R4 = 120/30 = 4 A;
I5 = Uab/R5 = 120/20 = 6 A.
3. Проверкой служит уравнение, составленное по первому закону Кирхгофа, при подстановке в нее рассчитанных числовых значений токов:
— I1 + I3 + I2 – I4 – I5 = 0 или — 3 + (-2) + 15 – 4 – 6 = 0.
Задача 1.9. Определить показание вольтметра в электрической цепи (рис. 1.1.21).
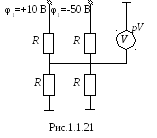
Решение
С учетом того, что ЭДС источника питания всегда направлена от минуса к плюсу, а заземленные узлы равно потенциальны, предлагаемая схема может быть изображена следующим образом (рис. 1.1.22)
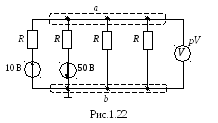
Показание вольтметра в такой схеме, как известно, определяется методом междуузлового напряжения как модуль напряжения между двумя узлами a и b :
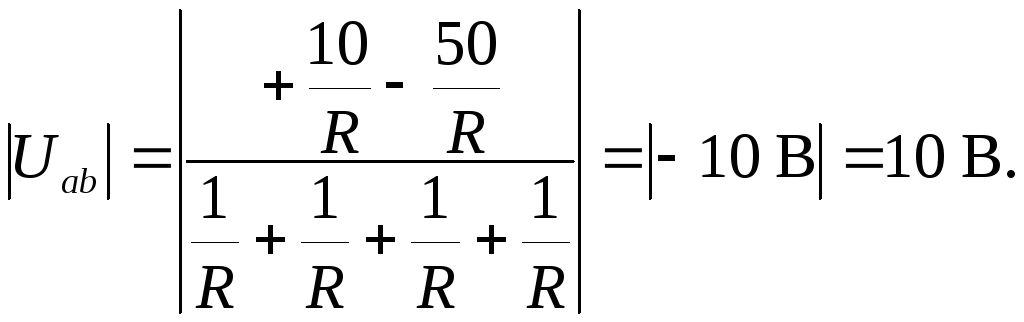
Задача 1.10. Для электрической цепи определить ток в ветви с резистором R4 методом активного двухполюсника (рис. 1.1.23).
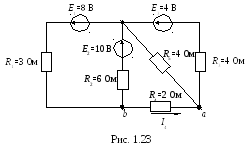
Решение
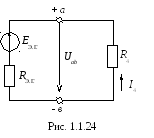
Согласно методу активного двухполюсника (или эквивалентного генератора ) воздействие всех источников питания на ветвь с неизвестным током заменяется воздействием одного, так называемого «эквивалентного», генератора, который на эквивалентной схеме замещения (рис.1.1.24) соединяется последовательно с исследуемой ветвью:
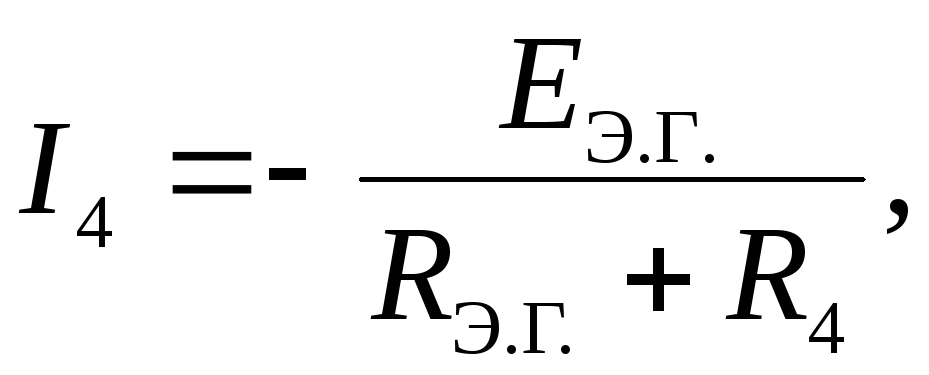
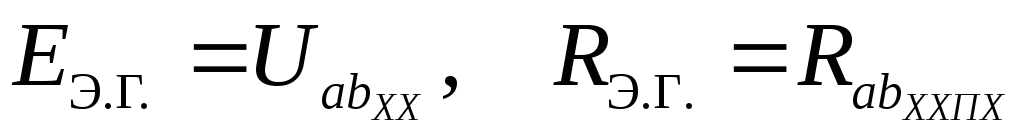
,
где 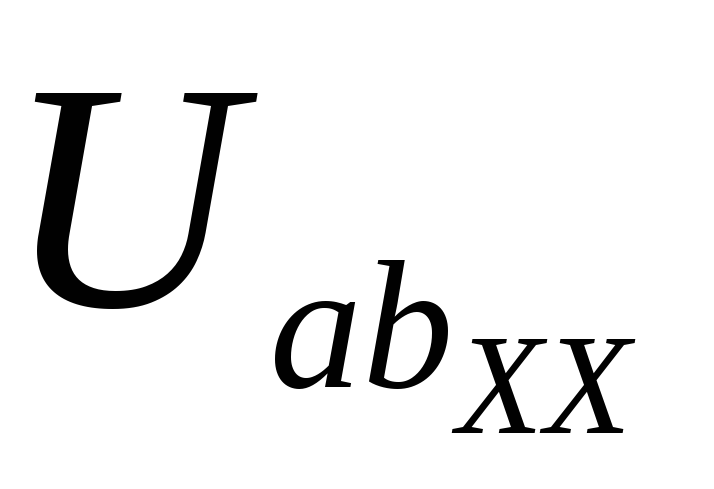 – напряжение между зажимами эквивалентного генератора а и b в режиме холостого хода;
– напряжение между зажимами эквивалентного генератора а и b в режиме холостого хода; 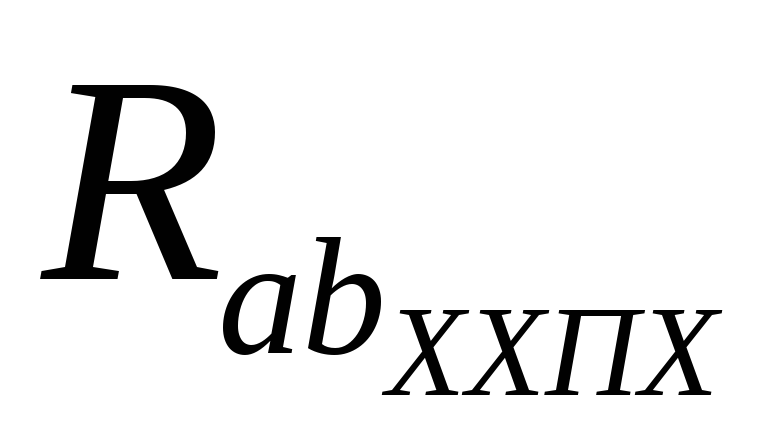 – сопротивление между зажимами а и b пассивного двухполюсника, полученного из схемы, соответствующей холостому ходу эквивалентного генератора.
– сопротивление между зажимами а и b пассивного двухполюсника, полученного из схемы, соответствующей холостому ходу эквивалентного генератора.
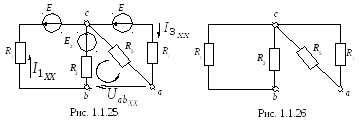
В рассматриваемом случае схема, соответствующая холостому ходу эквивалентного генератора, выглядит так (рис. 1.1.25.)
Пассивный двухполюсник (рис. 1.1.26) образуется при исключении источников питания, по сохранения их внутренних сопротивлений (в данном случае нулевых).
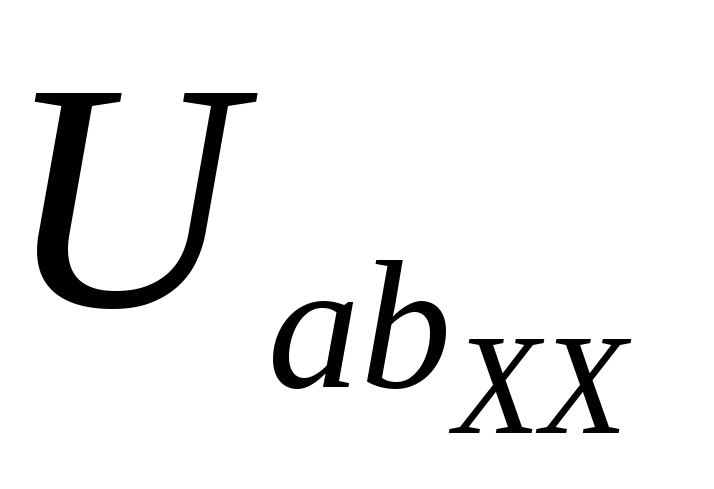
1. Определение ЭДС эквивалентного генератора (рис. 1.1.25). В двухконтурной схеме определяются токи в ветвях и далее на основе двух законов Кирхгофа в контуре aсb расcчитывается :
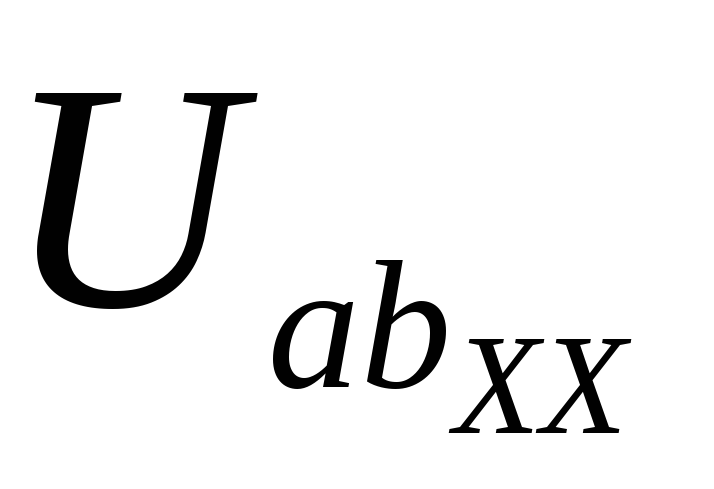
-E2 = R5I3хх + R2I1хх –
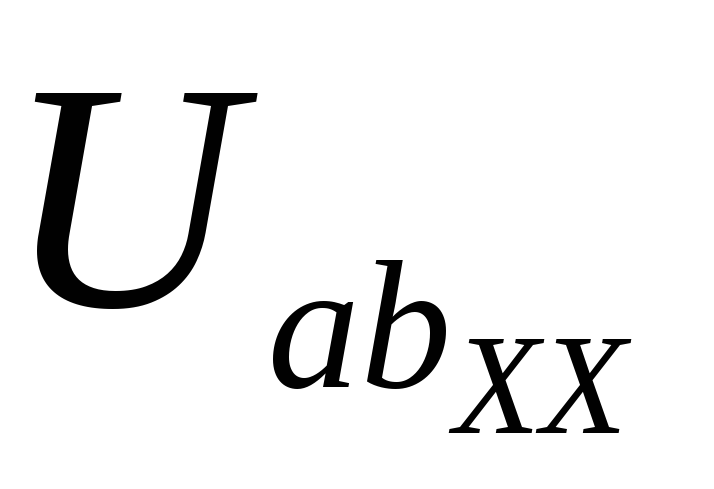
или = E2 + R5I3хх + R2I1хх =10 + 4(-0,5) + 6(-2) = — 4 В.
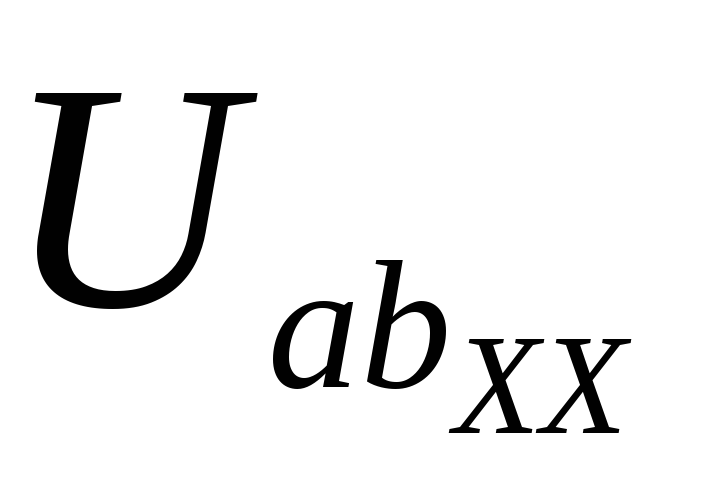
Таким образом, = — 4 В.
2. Определение внутреннего сопротивления эквивалентного генератора (рис. 1.1.26). Как видно, R1 и R2 соединены параллельно друг другу, R5 и R3 –аналогично, между собой они соединены последовательно, поэтому:
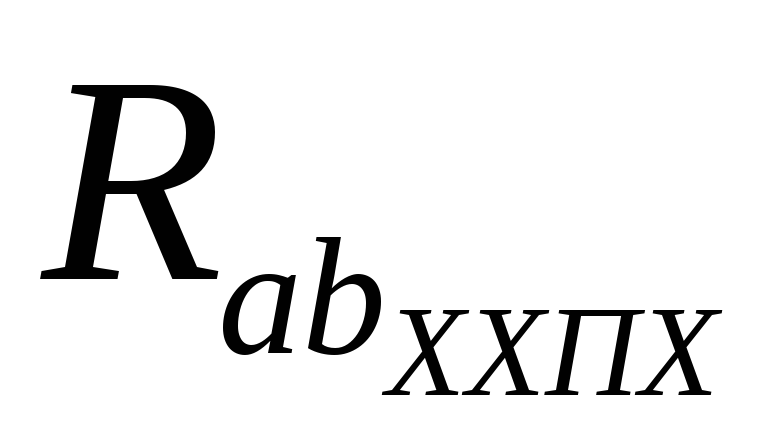
 = R1R2/(R1 + R2) +R3R5/(R3 + R5) = 36/(3+6) + 44/(4+4) = 4 Ом,
= R1R2/(R1 + R2) +R3R5/(R3 + R5) = 36/(3+6) + 44/(4+4) = 4 Ом,
или RЭ.Г. = = 4 Ом.
3. Определение тока в исследуемой ветви (рис. 1.1.24)
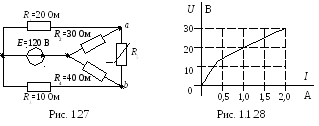
Задача 1.11. В электрической цепи (рис.1.1.27) определить ток в ветви с линейным элементом R5. Вольтамперная характеристика (ВАХ) нелинейного элемента (НЭ) приведена на рис. 1.1.28.
1
 .
.
Определение параметров эквивалентного генератора
Для определения тока в одной ветви схемы (в рассматриваемом случае, в ветви с НЭ) используется метод эквивалентного генератора. Эквивалентная схема замещения исходной цепи, а так же схемы эквивалентного генератора на холостом ходу и пассивного двухполюсника приводится на рис. 1.1.29 и 1.1.30.
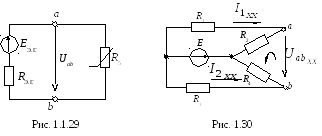
А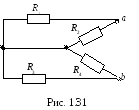 налогично решению предыдущей задачи ЭДС эквивалентного генератора ЕЭ.Г. =
налогично решению предыдущей задачи ЭДС эквивалентного генератора ЕЭ.Г. =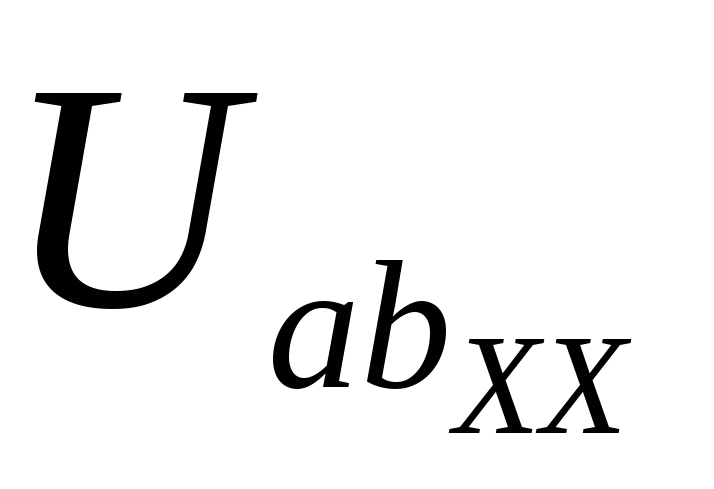 , причем (рис. 1.1.30)
, причем (рис. 1.1.30)
—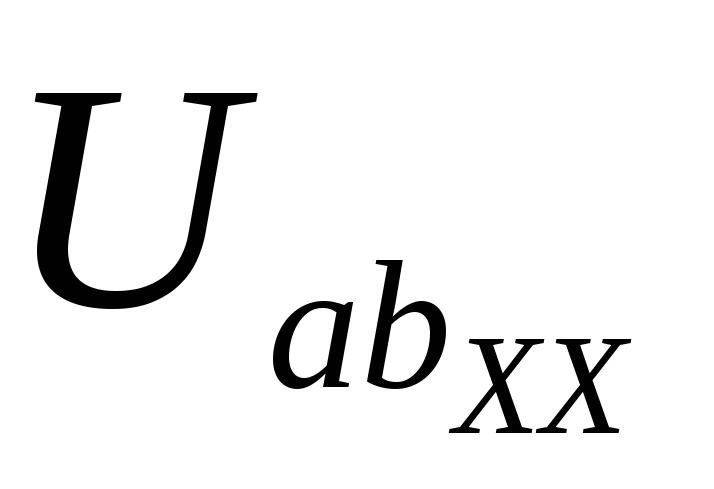 + R2
+ R2 — R4
— R4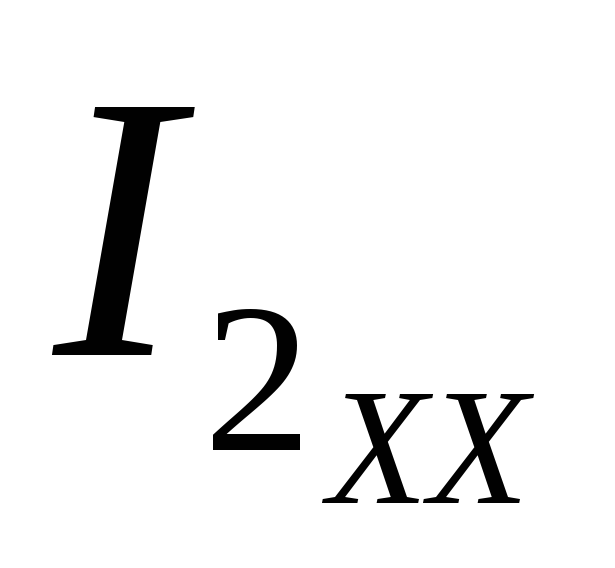 = 0,
= 0,
то есть EЭ.Г.= 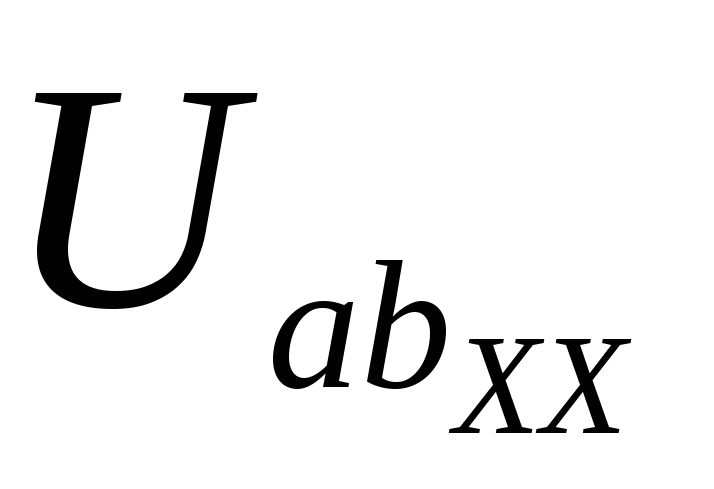 =+ R2
=+ R2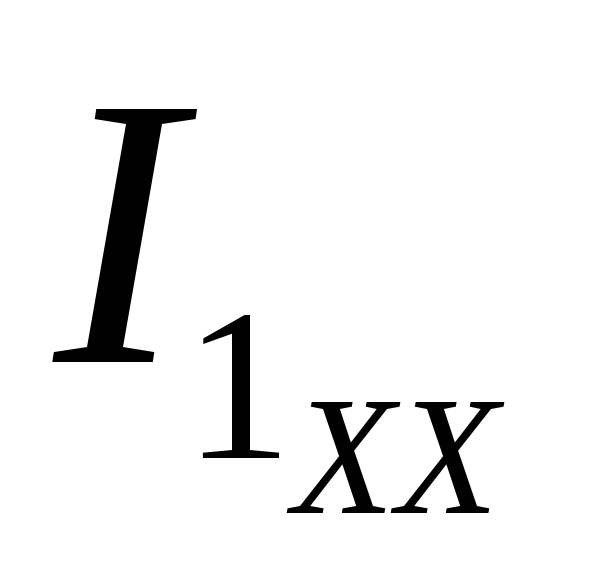 — R4
— R4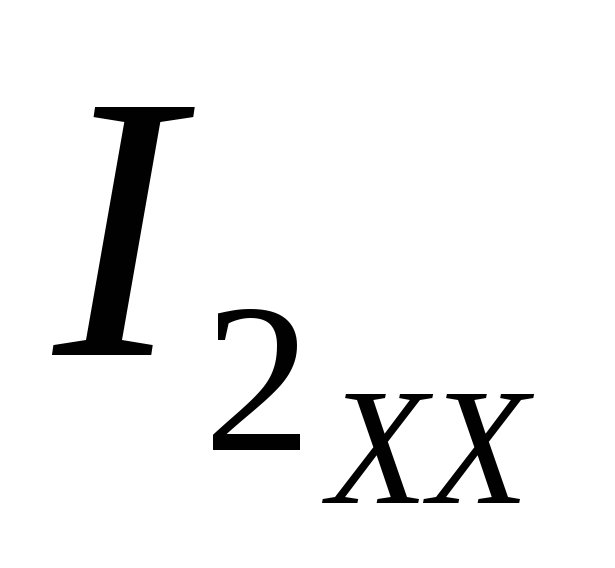 .
.
Токи 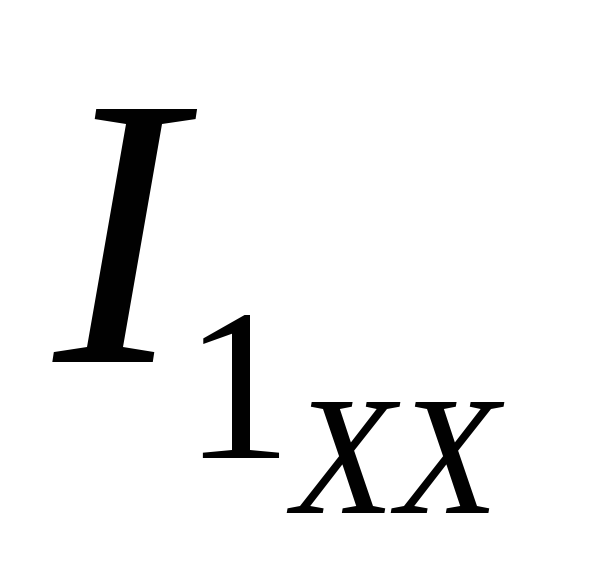 и
и 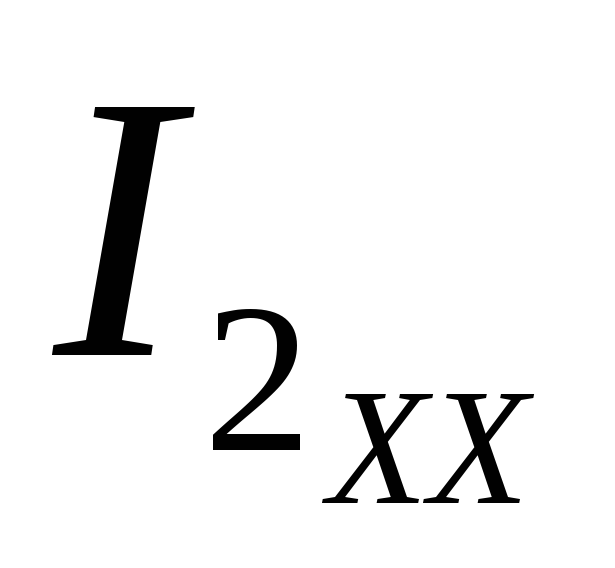 определяются любым известным методом, например,
определяются любым известным методом, например,
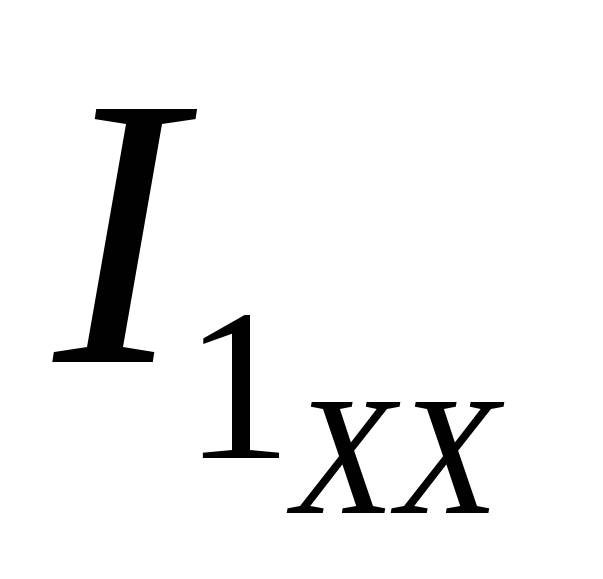
= — E / (R1 + R2) = -120 / (20 + 30) = -2,4 A;
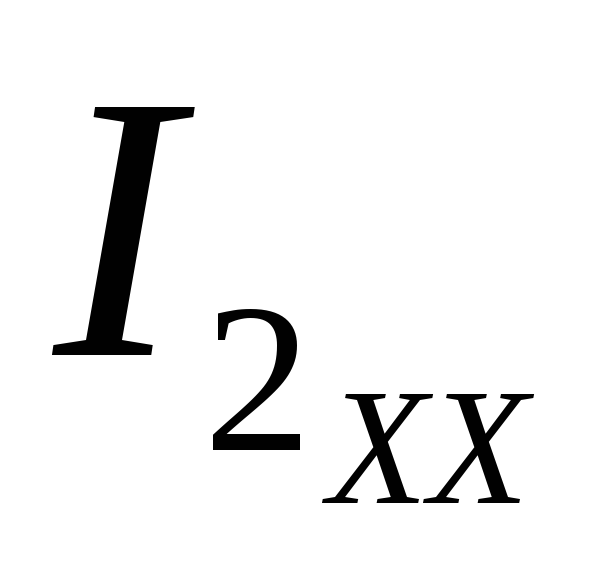
= -E / (R3 + R4) = -120 / (10 + 40) = -2,4 A.
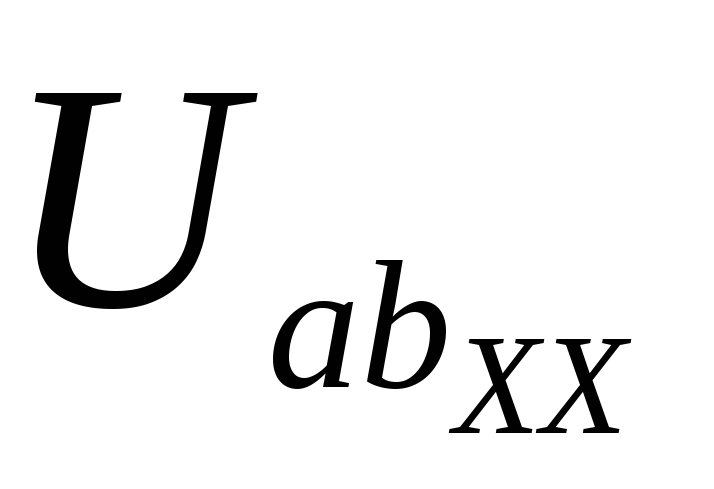
Тогда EЭ.Г. == 30(-2.4) — 40 (-2,4) = 24 В.
Внутреннее сопротивление эквивалентного генератора (рис. 1.1.31)
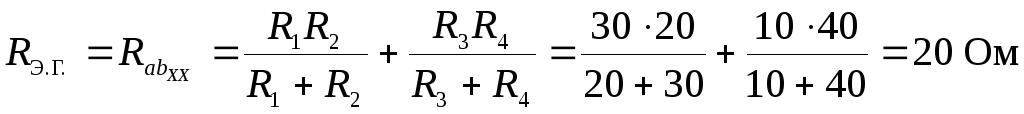
.
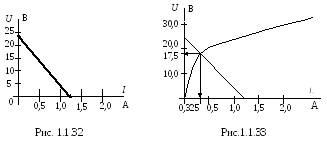
Таким образом, внешняя характеристика эквивалентного генератора имеет вид (рис. 1.1.32)
Стрелочный вольтметр


И хоть мы уже давно привыкли к цифровым вольтметрам, в природе всё ещё встречаются и стрелочные.
В некоторых случаях их применение может быть более удобным и практичным, чем использование современных цифровых.
Если в ваши руки попал стрелочный вольтметр, то желательно узнать его основные характеристики. Их легко определить по шкале и надписях на ней. В мои руки попал встраиваемый вольтметр М42300.

Внизу, под шкалой, как правило, есть несколько значков и указана модель прибора. Так, значок в виде подковы (или изогнутого магнита) означает, что это прибор магнитоэлектрической системы с подвижной рамкой.
На следующем снимке можно разглядеть такую подковку.

Горизонтальная чёрточка указывает на то, что данный измерительный прибор рассчитан на работу с постоянным током (напряжением).
Тут же стоит уточнить, почему речь идёт о постоянном токе. Не секрет, что стрелочными бывают не только вольтметры, но и огромное количество других измерительных приборов, например, тот же аналоговый амперметр или омметр.
Действие любого стрелочного прибора основано на отклонении катушки в поле магнита при прохождении постоянного тока по этой самой катушке. Чтобы отобразить с помощью стрелки показания на шкале прибора, ток должен быть постоянным.
Если он будет переменным, то стрелка будет отклоняться вправо-влево с частотой переменного тока, который протекает через обмотку катушки. Чтобы измерить величину переменного тока или напряжения в измерительный прибор встраивают выпрямитель.
Именно поэтому, под шкалой прибора указывается тип тока, с которым он способен работать: постоянным или переменным.
Далее на шкале прибора можно обнаружить целое или дробное число, вроде 1,5; 1,0 и подобное. Это класс точности прибора, выраженный в процентах %. Понятно, чем меньше число, тем лучше – показания будут точнее.
Также можно увидеть такой знак – две пересекающиеся черты под прямым углом. Этот знак указывает на то, что рабочее положение прибора вертикальное.
При горизонтальном положении показания могут быть менее точные. Иными словами прибор может «врать». Стрелочный вольтметр с таким значком лучше устанавливать в прибор вертикально и исключить существенный наклон.
А вот такой знак говорит о том, что рабочее положение прибора – горизонтальное.
Ещё один интересный знак – пятиконечная звезда с цифрой внутри.
Данный знак предупреждает о том, что между корпусом прибора и его магнитоэлектрической системой напряжение не должно превышать 2кВ (2000 вольт). На это стоит обращать внимание при эксплуатации вольтметра в высоковольтных установках. Если вы планируете использовать его в блоке питания на 12 – 50 вольт, то беспокоиться не стоит.
Как считывать показания со шкалы стрелочного вольтметра?
Для тех, кто впервые видит шкалу прибора, возникает вполне резонный вопрос: «А как же считывать показания?» На первый взгляд ничего непонятно .
На самом деле всё просто. Чтобы определить минимальное деление шкалы нужно определить ближайшее число (цифру) на шкале. Как видим на шкале нашего М42300 – это 2.

Далее считаем количество промежутков между чёрточками до первого числа или цифры – в нашем случае до 2. Их оказывается 10. Далее делим 2 на 10, получаем 0,2. То есть, расстояние от одной маленькой чёрточки до соседней, равно – 0,2 вольта.
Вот мы и нашли минимальное деление шкалы. Таким образом, если стрелка прибора отклонится на 2 маленьких деления, то это будет означать, что напряжение равно 0,4V (2 * 0,2V = 0,4V).
В наличии уже знакомый нам встраиваемый вольтметр модели М42300. Прибор предназначен для измерения постоянного напряжения до 10 вольт. Шаг измерения — 0,2 вольта.
Прикручиваем к клеммам вольтметра два провода (соблюдаем полярность!), и подключаем севшую батарейку на 1,5 вольта или любую попавшуюся.

Вот такие показания я увидел на шкале прибора. Как видим, напряжение батарейки равно 1 вольту (5 делений * 0,2V = 1V). Пока фотографировал, стрелка вольтметра упорно двигалась к началу шкалы — батарейка отдавала последние «соки».

Кроме этого мне стало интересно, какой ток потребляет сам стрелочный вольтметр. Поэтому вместо батарейки я подключил блок питания и выставил на выходе 10 вольт — чтобы стрелка прибора отклонилась на всю шкалу. Далее я подключил в разрыв цепи цифровой мультиметр и измерил ток.

Оказалось, ток, потребляемый стрелочным вольтметром, составил всего 1 миллиампер (1 мА). Его достаточно, чтобы стрелка отклонилась на всю шкалу. Это очень мало. Поясню свой намёк.
Получается, что стрелочный вольтметр экономичнее цифрового. Посудите сами, любой цифровой измерительный прибор имеет дисплей (ЖК или светодиодный), контроллер, а также буферные элементы для управления дисплеем. И это только часть его схемы. Всё это потребляет ток, садит батарею или аккумулятор. И если в случае вольтметра с жидкокристаллическим дисплеем потребляемый ток невелик, то при наличии активного светодиодного индикатора, потребляемый ток будет уже существенный.
Вот и получается, что для портативных приборов с автономным питанием иногда разумнее использовать классический стрелочный вольтметр.
При подключении вольтметра к цепи следует помнить о нескольких простых правилах.
- Во-первых, вольтметр (любой, хоть цифровой, хоть стрелочный) необходимо подключать параллельно той цепи или элементу, напряжение на котором планируется измерять или контролировать.
- Во-вторых, следует учитывать рабочий диапазон измерений. Узнать его легко – достаточно взглянуть на шкалу и определить последнее число на шкале. Это и будет граничное напряжение для измерения данным вольтметром. Естественно, есть и универсальные вольтметры, с выбором предела измерения, но сейчас речь идёт о встраиваемом стрелочном вольтметре с одним пределом измерения.
Надеюсь, теперь вам будет проще определить основные характеристики стрелочного вольтметра, а самое главное, применить его в своих самоделках, например, встроив его в блок питания с регулируемым выходным напряжением . А если сделать светодиодную подсветку его шкалы, то он будет выглядеть вообще шикарно! Согласитесь, такой стрелочный вольтметр будет смотреться стильно и эффектно.
Правила подключения вольтметра в электрическую цепь
- Зажимы вольтметра нужно подсоединять к тем точкам цепи, между которыми надо измерить напряжение. Такое подключение называется параллельным (рисунок 3).
Подробнее об особенностях параллельного подключения приборов вы узнаете в следующих уроках.
- У одного из зажимов вольтметра стоит знак “+”. Провод, подключенный к этому зажиму, необходимо соединять с проводом, идущим от положительного полюса источника тока (рисунок 4). Если подключить прибор неправильно, то стрелка вольтметра просто начнет отклоняться в другую сторону.
Измерение напряжения вольтметром в электроприборе
Используя вышеприведенные правила, давайте попробуем на практическом опыте измерить напряжение.
Допустим, его необходимо измерить на электрической лампе. Соберем электрическую цепь, состоящую из ключа, электрической лампы, источника тока. Подключим последовательно в эту цепь амперметр. Вольтметр подсоединяем параллельно к зажимам лампы (рисунок 5).
Схема такой электрической цепи будет выглядеть следующим образом (рисунок 6).
Обратите внимание, что амперметром здесь мы измеряем силу тока в электрической лампе. Вольтметром мы измеряем ее напряжение.
Амперметр подключается последовательно, а вольтметр — параллельно.
А какой должна быть сила тока, проходящего через вольтметр, по сравнению с силой тока в цепи? Отличается ли она от силы тока во всей цепи?
Да, отличается. Вольтметр устроен таким образом, что сила тока, проходящего через него, крайне мала по сравнению с силой тока в самой электрической цепи. Это позволяет исключить изменение напряжения между теми точками, к которым подсоединен вольтметр. Это же и способствует получению более точных значений напряжения.
Ошибки, которые могут возникнуть
В процессе определения показаний вольтметра по схеме могут возникнуть некоторые ошибки. Рассмотрим некоторые из них:
1. Неправильное подключение схемы: Если схема подключена неправильно, то показания вольтметра могут быть неверными. Убедитесь, что все провода и элементы схемы подключены правильно, и проводник с минусом вольтметра соединен с общим проводом схемы.
2. Плохой контакт: Если в схеме имеются провода с плохим контактом, то показания вольтметра могут быть непостоянными или неверными. Обратите внимание на качество контакта и, при необходимости, проверьте и отремонтируйте провода и соединения.
3. Сопротивление проводов: Если в схеме присутствуют провода с большим сопротивлением, то показания вольтметра могут быть неправильными. Убедитесь, что провода имеют низкое сопротивление, чтобы минимизировать потери напряжения и обеспечить точные показания вольтметра.
4. Сбои в работе вольтметра: Иногда вольтметр может работать неправильно из-за сбоев в его работе. В этом случае, проверьте состояние вольтметра, убедитесь, что он работает нормально, и при необходимости замените или отремонтируйте его.
5. Воздействие внешних факторов: Вольтметр может быть подвержен воздействию внешних факторов, таких как магнитные поля или электромагнитные излучения. Это может привести к искажению показаний вольтметра. Проверьте, что вольтметр не подвержен воздействию таких факторов, и при необходимости переставьте или защитите его от таких воздействий.
Пример неверных или сопряженных с ошибками показаний вольтметра:
Sally-Face.ru — это отличный ресурс для тех, кто ищет свежие вопросы и ответы на самые разные темы. На сайте собрана огромная база знаний, которая поможет вам быстро и легко найти ответы на интересующие вас вопросы.
Одной из главных особенностей сайта является его актуальность. Администрация регулярно обновляет базу данных, добавляя новые вопросы и ответы на самые разные темы. Благодаря этому вы всегда можете быть уверены в том, что найдете на сайте самую актуальную информацию.
Кроме того, на сайте Sally-Face.ru вы можете найти ответы на вопросы, которые вам не удалось найти на других ресурсах. На сайте собраны ответы на самые разные вопросы, начиная от технических и заканчивая медицинскими.
Если вы обнаружили неточность или ошибку в ответе на сайте, вы всегда можете сообщить об этом администрации. Для этого на сайте есть специальная форма обратной связи, которую можно заполнить, чтобы сообщить об ошибке.
В целом, сайт Sally-Face.ru является одним из лучших ресурсов для тех, кто ищет свежие и актуальные ответы на самые разные вопросы. Благодаря его удобному интерфейсу и огромной базе данных вы можете быстро и легко найти ответы на все свои вопросы.
Измерение напряжения. Вольтметр.
Прибор, предназначенный для измерения напряжения, называется вольтметр. И, в отличие от амперметра, в цепь он включается параллельно участку цепи, напряжение на котором необходимо определить. И, опять же, в противоположность идеальному амперметру, имеющему нулевое сопротивление, сопротивление идеального вольтметра должно быть равно бесконечности. Давай разберемся, с чем это связано:
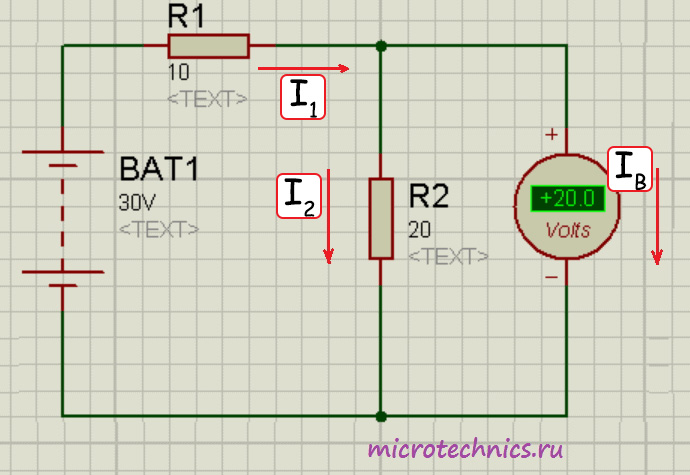
Если бы в цепи не было вольтметра, ток через резисторы был бы один и тот же и определялся по Закону Ома следующим образом:
I_1 = I_2 = frac = frac = 1
Итак, величина тока составила бы 1 А, а соответственно напряжение на резисторе 2 было бы равно 20 В. С этим все понятно, а теперь мы хотим измерить это напряжение вольтметром и включаем его параллельно с R_2 . Если бы сопротивление вольтметра было бы бесконечно большим, то через него просто не потек бы ток ( I_B = 0 ), и прибор не оказал бы никакого воздействия на исходную цепь. Но поскольку r_В имеет конечную величину и не равно бесконечности, то через вольтметр потечет ток. В связи с этим напряжение на резисторе R_2 уже не будет таким, каким бы оно было при отсутствии измерительного прибора. Вот поэтому идеальным был бы такой вольтметр, через который не проходил бы ток. Как и в случае с амперметром, есть специальный метод, который позволяет увеличить пределы измерения напряжения для вольтметра. Для осуществления этого необходимо включить последовательно с прибором добавочное сопротивление, величина которого определяется по формуле:
R_Д = r_Вmedspace (nmedspace-medspace 1)
Это приведет к тому, что показания вольтметра будут в n раз меньше, чем значение измеряемого напряжения. По традиции давайте рассмотрим небольшой практический пример:
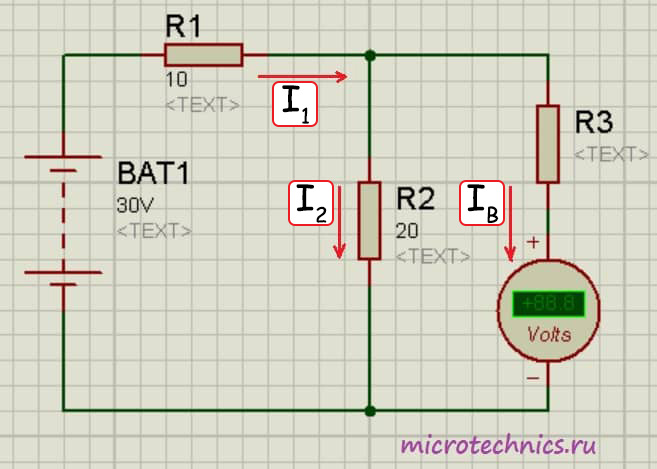
Здесь мы добавили в цепь добавочное сопротивление R_3 . Перед нами стоит задача измерить напряжение на резисторе R_2:medspace U_2 = R_2medspace I_2 . Давайте определим, какой результат при таком включении выдаст нам вольтметр:
U_2 = I_2medspace R_2 = U_В + I_Вmedspace R_3
Подставим в эту формулу выражение для расчета сопротивления добавочного резистора:
U_2 = U_В + I_Вmedspace (r_Вmedspace (nmedspace-medspace 1)) = U_В + I_Вmedspace r_Вmedspace nmedspace-medspace I_Вmedspace r_В = U_В + U_Вmedspace nmedspace-medspace U_В = U_Вmedspace n
Таким образом: U_В = frac . То есть показания вольтметра будут в n раз меньше, чем величина напряжения, которое мы измеряли. Так что, используя данный метод, возможно значительно увеличить пределы измерения вольтметра. В завершении статьи пару слов об измерении сопротивления и мощности. Для решения обеих задач возможно совместное использование амперметра и вольтметра. В предыдущих статьях (про мощность и сопротивление) мы подробно останавливались на понятиях сопротивления и мощности и их связи с напряжением и сопротивлением, таким образом, зная ток и напряжение электрической цепи можно произвести расчет нужного нам параметра. Ну а кроме того есть специальные приборы, которые позволяют произвести измерения сопротивления участка цепи (омметр) и мощности (ваттметр). В общем-то, на этом, пожалуй, на сегодня закончим, следите за обновлениями!
Решение

Найдите показания амперметра в цепи
Построив векторную диаграмму, я получил ответ AC= 8 A. Подскажите, пожалуйста, правильно ли это?
Найдите показания вольтметра
Найти показания вольтметра в электрической цепи (тема про трансформаторы) Помогите:(
Найдите показания вольтметра и ваттметра
Здравствуйте, я не знаю, как читать вольтметр и ваттметр.
Найдите показания амперметра и вольтметра
Пожалуйста, помогите мне решить эту проблему. XL=10 Ом XC=10 Ом R1=10 Ом R2=10 Ом U=100 В Требуется.
Найдите напряжение и снимите показания вольтметра
Вам необходимо найти напряжение и снять показания вольтметра. X1 X2 X3 X4 начал искать, но потом.
Падение напряжения на сопротивлении R V (Вы можете не вычислять показания вольтметра, а сразу сказать, что U V = E поскольку вольтметр подключен параллельно батарее, а внутреннее сопротивление батареи и амперметра не учитывается)
Как найти показания на вольтметре
Решение:
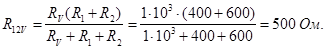
Ток, протекающий через сопротивление R 12 V (показания амперметра)
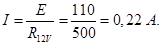
Падение напряжения на сопротивлении R V (Показания вольтметра не могут быть рассчитаны, но могут быть немедленно сообщены как U V = E поскольку вольтметр подключен параллельно батарее, а внутреннее сопротивление батареи и амперметра не учитывается)
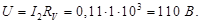
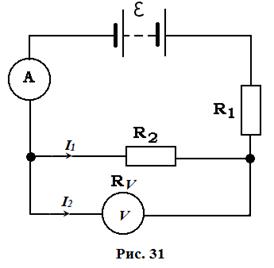
Ответ: 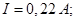
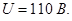
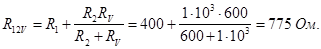
Ток, протекающий через сопротивление R 12 V (показания амперметра)
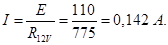
Падение напряжения на сопротивлении R V (показания вольтметра)
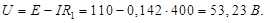
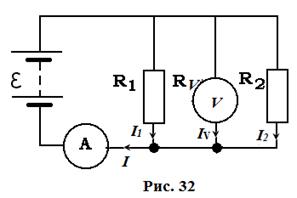
Ответ: 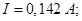
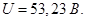
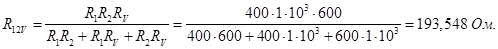
Ток, протекающий через сопротивление R 12 V (показания амперметра)
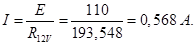
Падение напряжения на сопротивлении R V (Показания вольтметра не могут быть рассчитаны, но могут быть сразу представлены как U V = E поскольку вольтметр подключен параллельно батарее и внутреннее сопротивление батареи и амперметра не учитывается)
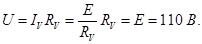
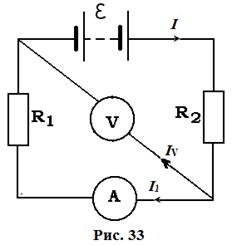
Ответ: 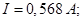
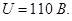
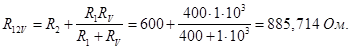
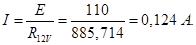
Ток, протекающий через сопротивление R 2
Падение напряжения на сопротивлении R 2
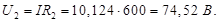
Падение напряжения на сопротивлении R V (показания вольтметра)
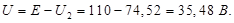
Ток, протекающий через сопротивление R R 1 (показания амперметра)
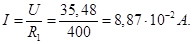
Ответ: 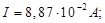
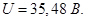
- Разветвленные цепи. Правило обхода цепи – Электричество и магнетизм – Киберфорум .
- Топология электрической цепи (Лекция N 2) .
- Как найти напряжение источника .
- Измерение тока и напряжения. Вольтметр и амперметр .
- Измерительный инструмент – это инструмент для измерения. Что такое измерительный инструмент? .
- Пример проблемы с шунтирующим сопротивлением .
- Закон Ома для полной цепи .




