Длина волны — это одна из важных характеристик волновых процессов, которая позволяет определить расстояние между двумя соседними точками волны, на которых наблюдается одна и та же фаза колебаний. Зная длину волны, можно предсказывать свойства волн и использовать их в различных областях науки и техники.
Одним из способов определить длину волны является анализ графика зависимости физической величины от времени или пространственной координаты. Для этого необходимо определить период колебаний и скорость распространения волны.
Период колебаний можно найти по графику, определяя временной интервал между двумя ближайшими точками, на которых достигается одна и та же фаза колебаний. Скорость распространения волны можно найти, измерив фиксированное расстояние между двумя соседними точками, на которых достигается одна и та же фаза колебаний, и разделив его на время, за которое волна проходит это расстояние.
После определения периода колебаний и скорости распространения волны, можно вычислить длину волны по формуле: длина волны = скорость распространения волны * период колебаний. Таким образом, анализ графика позволяет определить длину волны и получить информацию о свойствах волны.
Как измерить длину волны: практическое руководство
Измерение длины волны может быть полезным при изучении оптики, звука и других физических явлений. Определить длину волны по графику можно сравнивая расстояние между двумя точками на графике с периодом колебаний.
Для начала, убедитесь, что вы имеете график колебаний, на котором видны один или несколько полных периодов. Если график представлен в виде временной зависимости, у вас будет несколько периодов колебаний.
Выберите две точки на графике, которые соответствуют одному полному периоду колебаний. Обычно точками выбирают гребни или впадины, где амплитуда колебаний меняется наиболее значительно.
Измерьте расстояние между этими двумя точками на графике. Вы можете использовать линейку или другое измерительное устройство для точного измерения. Запишите это расстояние величиной в метрах.
Следующим шагом является определение периода колебаний. Это время, за которое происходит одно полное колебание, выраженное в секундах. Обычно период представляет собой горизонтальную величину на графике, отмеченную временными метками.
Используйте измерительное устройство, чтобы определить временной интервал между двумя ближайшими временными метками, соответствующими одному полному периоду колебаний. Запишите этот период величиной в секундах.
Теперь, чтобы найти длину волны, разделите значение периода на измеренное расстояние на графике. Например, если период равен 0,1 секунды, а расстояние между двумя точками на графике равно 0,02 метра, то длина волны будет равна 0,1 / 0,02 = 5 метров.
Итак, измерение длины волны по графику может быть достаточно простым. Следуя этому практическому руководству, вы сможете определить длину волны и изучать различные физические явления с графической точки зрения.
9 класс, 35 урок, Длина волны. Скорость распространения волн
Длина волны. Связь длины волны со скоростью её распространения и периодом (частотой)
Скорость волны зависит от строения вещества и взаимодействия между её молекулами (атомами). Поэтому в различных средах скорость одной и той же волны будет отличаться.
Помимо скорости, важной характеристикой волны является длина волны.
Длина волны — расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Рассмотрим процесс передачи колебаний от точки к точке при распространении поперечной волны.
Используется модель, в которой частицы среды заменяют шариками. Для удобства их можно пронумеровать (рис. (1)).
Частицы среды связаны между собой межмолекулярными силами взаимодействия, поэтому волна передаётся от одной частицы к другой.
![]()
Рис. (1). Модель упругой среды для демонстрации колебаний
Отклоним первый шарик от положения равновесия. Силы притяжения передадут движение второму, третьему шарику. Каждый элемент вещества (молекула, атом) повторит движение первой частицы с запаздыванием, которые называют сдвигом фазы. Это запаздывание зависит от расстояния, на котором находится рассматриваемый шарик по отношению к первому шарику.
Предположим, что первый шарик достиг максимального смещения от положения равновесия (рис. (2)). В этот момент четвёртый шарик только начнет движение, следовательно, он отстаёт от первого на (1/4) колебания.

Рис. (2). Изображение максимального смещения от положения равновесия первого шарика
В момент времени, когда смещение четвертого шарика будет наибольшим (рис. (3)), седьмой шарик будет отставать от него на (1/4) колебания. А если рассмотреть отставание седьмого шарика от первого, то оно составляет (1/2) колебания.

Рис. (3). Изображение максимального смещения от положения равновесия четвёртого шарика
Между седьмым и четвёртым шариком, а также седьмым и десятым (1/4) часть колебания (рис. (4)).

Рис. (4). Изображение максимального смещения от положения равновесия седьмого шарика
Первый и тринадцатый шарик совершают одно колебание, то есть двигаются в одной фазе (рис. (5)). Это значит, что между ними все шарики с первого по двенадцатый проходят полный колебательный процесс или составляют одну волну.
Примеры расчета длины волны для звуковых, электромагнитных и радиоволн
Задача №1
Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2
Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3
Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.
Связь со скоростью
Чтобы вывести формулу скорости через длину волны, нужно вспомнить формулу скорости из кинематики — это раздел физики, в котором изучается движение тел без учета внешнего воздействия).
Формула скорости
= S/t
Переходя к волнам, можно провести следующие аналогии:
- путь — длина волны
- время — период
А для скорости даже аналогия не нужна — скорость и в Африке скорость.
Формула скорости волны
= λ/T
λ — длина волны [м]
Задачка
Лодка совершает колебания на волнах. За 40 с она совершила 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
Решение:
Возьмем формулу скорости:

Резонанс
Если громко говорить в одном помещении с гитарой — можно услышать, как на ней начал играть призрак. На самом деле частота струны совпала с частотой голоса и возник резонанс.
На графике ниже можно увидеть, что на некоторой частоте резко увеличивается амплитуда. Эта частота называется частотой резонанса.
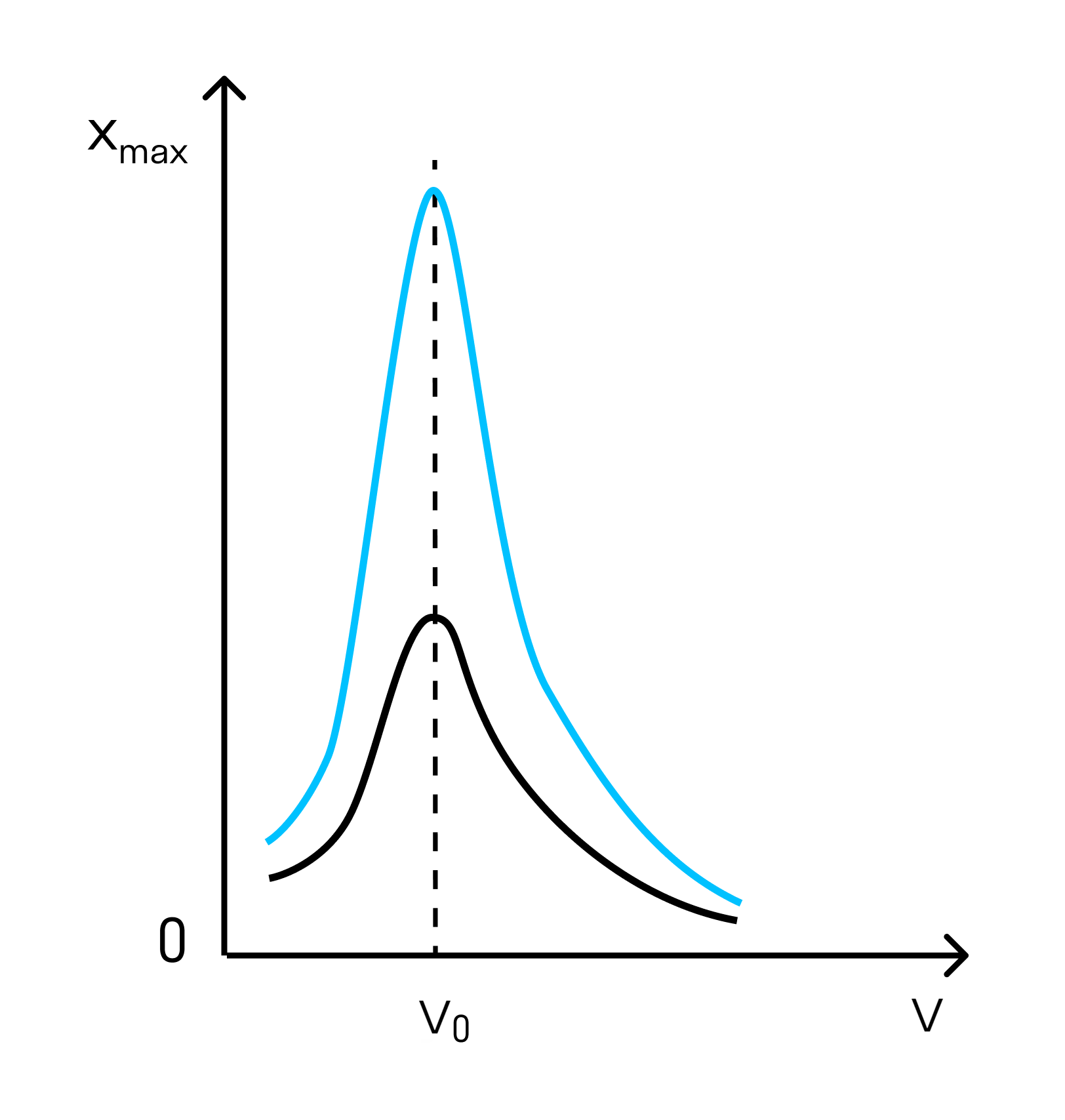
Частота — это величина, обратная периоду. Она показывает, за какое время происходит одно колебание.
Формула частоты
ν = N/t
N — количество колебаний [—]
В мире существует очень много историй про то, как солдаты шли в ногу по мосту, он впал в резонанс и все провалились. А вот еще одна история про гидрологов — как говорится, из первых уст
Команда гидрологов — специалистов по внутренним водам — работала на Алтае и изучала местную реку. Через реку был протянут веревочный мост, а по центру моста стояла лебедка, которая помогает поднять пробу воды из речки, не спускаясь до нее.
В один из дней экспедиции начался сильный, почти штормовой, ветер. Исследователи работали на мосту, а когда поняли, что находиться на веревочной конструкции в такой сильный ветер небезопасно, начали с него уходить. Как только последний человек из команды сделал шаг с моста на землю, мост вместе с лебедкой разнесло в щепки. Это произошло из-за того, что частота ветра совпала с собственной частотой раскачивающегося моста. Хорошо, что история закончилась именно так.
Длина и скорость волны.
Любая волна распространяется с некоторой скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.
Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.
Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.
Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

,
где v — скорость волны, Т — период колебаний в волне, λ (греческая буква лямбда) — длина волны.

Формула выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте v, т. е. Т = 1/v, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:

,

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.
Длина волны — это пространственный период волны. На графике волны (рис. выше) длина волны определяется как расстояние между двумя ближайшими точками гармонической бегущей волны, находящимися в одинаковой фазе колебаний. Это как бы мгновенные фотографии волн в колеблющейся упругой среде в моменты времени t и t + Δt. Ось х совпадает с направлением распространения волны, на оси ординат отложены смещения s колеблющихся частиц среды.
Частота колебаний в волне совпадает с частотой колебаний источника, т. к. колебания частиц в среде являются вынужденными и не зависят от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.
Длина волны
Длина электромагнитной волны в среде короче, чем в вакууме:
где n = ε μ > 1 >>1> — 1 / ε >> , показывающую, во сколько раз длины волны в среде короче по отношению к длине волны в вакууме, которую называют коэффициентом укорочения. Например, для полиэтилена (используется в радиочастотном диапазоне как изоляционный материал с малыми потерями) ε ≈ 2,56, и коэффициент укорочения приближенно равен 1/1,5 ≈ 0,67.
Напротив, длина электромагнитной волны (поперечномагнитной, поперечноэлектрической) в Волны де Бройля [ ]
Волнам де Бройля также соответствует определенная длина волны. Частице с энергией Е и импульсом p, соответствуют:
где h — Примеры [ ]
Видеоурок: длина волны
Приближённо, с погрешностью около 0,07 % рассчитать длину радиоволны в свободном пространстве можно так: 300 делим на частоту в мегагерцах, получаем длину волны в метрах. Другой способ — запомнить какую-нибудь удобную пару f ↔ λ, например, частоте 100 МГц соответствует длина волны 3 м; тогда оценив, во сколько раз требуемая частота выше или ниже 100 МГц, можно определить длину волны. Например, 1 МГц ниже 100 МГц в 100 раз, значит 1 МГц ↔ 3 м × 100 = 300 м
Примеры характерных частот и длин волн: частоте 50 радиовещательный FM-диапазон ) — 3 м; 900 (1800) МГц ( Wi-Fi ) — 12,5 см; 10 ГГц (бортовые Шаблон:Nobr [3] .
Примечания [ ]
- ↑ Определение не вполне корректно, поскольку (1) в одинаковой фазе колебания происходят и на фронте волны, и расстояние между точками на фронте может быть произвольным, в том числе и нулевым; (2) чтобы расстояние между двумя точками равнялось длине волны, колебание должно происходить не в одинаковой фазе, а со сдвигом фаз в 2π, и расположены точки должны быть вдоль линии распространения
- ↑ ГОСТ 18238-72. Линии передачи сверхвысоких частот. Термины и определения
- ↑ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин
- Шаблон:БСЭ3
- Шаблон:БСЭ3
Физические характеристики волны
Обратимся к рисункам д, е еще раз. Видно, что когда частица 1 находится в положении равновесия и движется вверх, частица 13 тоже находится в положении равновесия и движется вверх. Спустя четверть период частица 1 будет максимально отклонена от положения равновесия, ровно, как и частица 13. Так как частицы 1 и 13 движутся одинаково, говорят, что колебания этих частиц происходят в одинаковых фазах. Расстояние между этими частицами называют длиной волны.
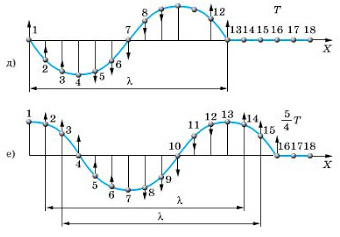
Внимание! В действительности частица 13 отстает по фазе от частицы 1 на 2π. Но поскольку такая разница фаз не приводит к различию в состояниях колеблющихся частиц, можно считать, что частицы колеблются в одинаковых фазах.
Длина волны — расстояние между двумя ближайшими точками волны, колеблющимися в одинаковых фазах.
Длина волны обозначается как λ (лямбда). Единица измерения длины волны — метр (м).
Согласно рисунку е, в одинаковых фазах колеблются частицы 1 и 13, 2 и 14, 3 и 15, 4 и 16. Поэтому расстояния между этими частицами равно длине волны. Но частицы 1 и 7, находящиеся на расстоянии λ 2 . . , колеблются в противоположных фазах. Посмотрите на рисунок д: когда 1 частица находится в положении равновесия и движется вверх, частица 7 находится в положении равновесия и движется низ. На рисунке е обе частицы максимально отклонены от положения равновесия, но в противоположных направлениях.
Волна распространяется на расстояние λ за время, равное периоду колебаний частиц вещества. Зная расстояние, на которое распространилась волна, и время, в течение которого это распространение происходило, можно найти скорость волны:
Но мы знаем, что период равен величине, обратной частоте колебаний:
Тогда скорость распространения волны равна:
Скорость волны равна произведению длины волны на частоту колебаний.
При распространении волны мы имеем дело с периодичностью двоякого рода:
- Во-первых, каждая частица среды совершает периодические колебания во времени. В случае гармонических колебаний (эти колебания происходят по синусоидальному или косинусоидальному закону) частота постоянна и амплитуда одинакова во всех точках. Колебания отличаются только фазами.
- Во-вторых, в данный момент времени форма волны повторяется в пространстве через отрезки длиной λ вдоль линии распространения волны. На рисунке ниже показан профиль волны в определенный момент времени (сплошная линия). С течением времени вся эта картина перемещается со скоростью v направо. Спустя промежуток времени ∆t волна будет иметь вид, изображенный на том же рисунке прерывистой линией.
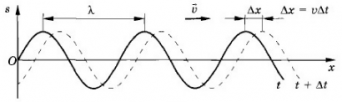
Пример №1. Определите скорость распространение волны на поверхности воды, если расстояние между ее гребнями равно 1 метру. Учитывайте, что мимо наблюдателя за 5 секунд прошло 10 волн.
Обычно под волной на воде люди понимают гребни — частицы воды, максимально отклоненные от положения равновесия. Расстояние между гребнями равно длине волны. Чтобы найти скорость распространения волны, нужно знать частоту колебания молекул воды. Ее можно вычислить по следующей формуле:
где n — количество «волн», прошедших мимо наблюдателя.
Тогда скорость волны равна:
v = λ ν = λ n t . . = 1 · 10 5 . . = 2 ( м с . . )
Уравнение бегущей волны
Определение
Бегущая волна — волна, распространяющаяся в пространстве.
Колебания гармонической волны в любой точке происходят по гармоническому закону с одной и той же амплитудой. Найдем уравнение, описывающее колебательный процесс в любой точке пространства при распространении гармонической волны.
Будем рассматривать волну, бегущую по длинному тонкому резиновому шнуру. Ось Ox направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение любой колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса необходимо знать значение s в любой точке шнура в любой момент времени. Следовательно, нужно знать вид функции:
Заставим конец шнура (точка х = 0) совершать гармонические колебания с частотой ω. Если начальную фазу колебаний считать равной 0, то колебания этой точки будут происходить по закону:
s = s m a x s i n ω t
s m a x — амплитуда колебаний (рис. а).
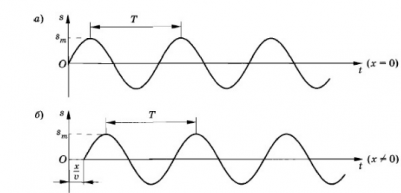
Колебания распространяются вдоль шнура (оси Ox) со скоростью v и в произвольную точку шнура с координатой х придут спустя время, которое можно определить следующим выражением:
Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. б). Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой smax, но с другой фазой:
Уравнение бегущей волны
s = s m a x s i n [ ω ( t − τ ) ] = s m a x s i n [ ω ( t − x v . . ) ]
Это уравнение называется уравнением бегущей волны, распространяющейся в положительном направлении оси Ox.
Пример №2. Уравнение бегущей волны имеет вид s ( x , t ) = 0 , 1 sin . ( 2 π t − x π 2 . . ) . Найдите частоту волны, скорость её распространения и длину.
Запишем уравнение бегущей волны:
s = s m a x s i n [ ω ( t − τ ) ] = s m a x s i n [ ω ( t − x v . . ) ]
Сопоставляя эти два уравнения можно определить, что циклическая частота и скорость распространения соответственно равны:
ω = 2 π ( р а д с . . )
Циклическую частоту также можно рассчитать по формуле:
Тогда частота волны равна:
ν = ω 2 π . . = 2 π 2 π . . = 1 ( Г ц )
Тогда длина волны равна:
λ = v ν . . = 4 1 . . = 4 ( м )
Текст: Алиса Никитина, 4.6k
Задание ЕГЭ-Ф-ДВ2023-21
Даны следующие зависимости величин: А) зависимость периода малых свободных колебаний математического маятника от длины нити маятника; Б) зависимость количества теплоты, выделяющегося при конденсации пара, от его массы; В) зависимость силы тока через участок цепи, содержащий резистор, от сопротивления резистора при постоянном напряжении на концах участка. Установите соответствие между этими зависимостями и видами графиков, обозначенных цифрами 1–5. Для каждой зависимости А–В подберите соответствующий вид графика и запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Алгоритм решения:
1. Установить, как период малых свободных колебаний математического маятника зависит от длины нити. Выбрать номер подходящего под эту зависимость графика.
2. Установить, как количество теплоты, выделяющееся при конденсации пара, зависит от его массы. Подобрать соответствующий график.
3. Установить, как сила тока на участке цепи с резистором зависит от сопротивления резистора при постоянном напряжении на концах участка. Выбрать соответствующий график.
4. Записать ответ в виде последовательности цифр выбранных графиков в порядке возрастания.
Решение:
Период колебаний математического маятника определяется формулой:
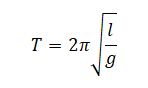
Видно, что период колебаний прямо пропорционален корню из длины нити математического маятника. Следовательно, графиком его зависимости от длины нити является горизонтально расположенная полупарабола — как на графике 1.
Количество теплоты, выделяющееся при конденсации пара, определяется формулой:
Следовательно, между количеством теплоты, выделяющимся при конденсации пара, и массой этого пара существует прямо пропорциональная связь. Поэтому график зависимости выглядит как прямая, выходящая из начала координат — как на графике 3.
Сила тока на участке цепи с резистором определяется законом Ома:
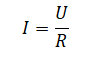
Следовательно, между силой тока и сопротивлением существует обратно пропорциональная связь. Графиком такой зависимости является гипербола — как на графике 5.
Следовательно, правильная последовательность цифр в ответе — 135.
Задание EF18242
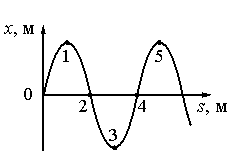
На рисунке показан профиль бегущей волны в некоторый момент времени. Разность фаз колебаний точек 1 и 5 равна
Алгоритм решения
- Определить характер движения указанных точек.
- По характеру движения точек определить их разность фаз.
Решение
Точки 1 и 5 соответствуют максимальной амплитуде колебаний. В этот момент они меняют направление движения (до этого двигались вверх, теперь меняют направление в противоположную сторону). Поскольку точки 1 и 5 движутся одинаково, можно считать, что они колеблются в одинаковых фазах. Это возможно, если разность фаз кратна 2π.
Задание EF22628
Какова скорость звуковых волн в среде, если при частоте 400 Гц длина волны λ = 4 м?
Алгоритм решения






