
Как я и обещал в статье про переменные резисторы (ссылка), сегодня речь пойдет о возможных способах соединения, в частности о последовательном соединении резисторов и о параллельном.
Последовательное соединение резисторов.
Давайте начнем с рассмотрения цепей, элементы которой соединены последовательно. И хоть мы и будем рассматривать только резисторы в качестве элементов цепи в данной статье, но правила, касающиеся напряжений и токов при разных соединениях, будут справедливы и для других элементов. Итак, первая цепь, которую мы будем разбирать выглядит следующим образом:
Здесь у нас классический случай последовательного соединения — два последовательно включенных резистора. Но не будем забегать вперед и рассчитывать общее сопротивление цепи, а для начала рассмотрим все напряжения и токи. Итак, первое правило заключается в том, что протекающие по всем проводникам токи при последовательном соединении равны между собой:
I = I_1 = I_2
А для определения общего напряжения при последовательном соединении, напряжения на отдельных элементах необходимо просуммировать:
U = U_1 + U_2
В то же время, по закону Ома для напряжений, сопротивлений и токов в данной цепи справедливы следующие соотношения:
U_1 = I_1R_1 = IR_1
U_2 = I_2R_2 = IR_2
Тогда для вычисления общего напряжения можно использовать следующее выражение:
U = U_1 + U_2 = IR_2 + IR_2 = I(R_1 + R_2)
Но для общего напряжения также справедлив закон Ома:
U = IR_0
Здесь R_0 — это общее сопротивление цепи, которое исходя из двух формул для общего напряжения равно:
R_0 = R_1 + R_2
Таким образом, при последовательном соединении резисторов общее сопротивление цепи будет равно сумме сопротивлений всех проводников. Например, для следующей цепи:
Общее сопротивление будет равно:
R_0 = R_1 + R_2 + R_3 + R_4 + R_5 + R_6 + R_7 + R_8 + R_9 + R_
Количество элементов значения не имеет, правило, по которому мы определяем общее сопротивление, будет работать в любом случае. А если при последовательном соединении все сопротивления равны ( R_1 = R_2 = . = R ), то общее сопротивление цепи составит:
R_0 = nR
В данной формуле n равно количеству элементов. С последовательным соединением резисторов разобрались, логичным образом переходим к параллельному.
Резистор – что это такое, назначение, виды, правила расчета
Элемент схемы, вызывающий сопротивление течению электрического тока и преобразующий его в тепловую энергию, называется резистором. Характеризуется компонент величиной сопротивления, выражаемой в «Омах». Чем выше значение этого параметра, тем сильнее электричество преобразуется в тепло.
Предназначается резистор для понижения или ограничения главных характеристик электрической цепи – силы тока и напряжения. При этом различаются между собой такие компоненты схемы не только по величине сопротивления, но также возможности его изменения – на 2 вида:
Найти общее сопротивление цепи со смешанным соединением резисторов
- Постоянные. Рабочая характеристика остается неизменной на протяжении всего периода эксплуатации. При перемене параметра устройство становится негодным и требует замены.
- Переменные. Сопротивление изменяется с помощью специального регулятора вручную – с целью подстройки под конкретные условия. В основе этого лежит принцип настройки различных приборов – звука в динамиках, степени нагрева в плитке и проч.
При этом в схему компонент можно установить в любом положении – так как контактные ножки одинаковы с обоих краев, и полярности не имеют.


Смотрите также:
Каталог компаний, что специализируются на электротехнических работах любой сложности
Независимо от того, каким способом выполняется соединение – последовательным, параллельным или смешанным – для внедрения в конкретную электросхему требуется правильный расчет резисторов. Для этого применяется известный закон Ома:
Например, имеется светильник на 6 вольт, требующий для работы силу тока 30 мА. Для поиска подходящего резистора значения подставляются в формулу:
Р = 6 / 0,03 А = 200 Ом.
Таким же способом можно рассчитать силу тока, проходящую через резистор известного номинала, и подобрать соответствующую лампочку.
Типы соединения
В электросхемах резисторы соединяются 3-мя способами:
В этом случае крайний контакт последующего элемента стыкуется с начальным контактом предыдущего. Таким образом, компоненты выстраиваются в одну линию.
При этом общее сопротивление цепи равняется сумме участников – то есть их величины просто складываются. Например, если взять 4 одинаковых элемента по 2 кОм, то в итоге получится = 2 + 2 + 2 + 2 = 8 кОм.

На заметку! Резисторы характеризуются не только сопротивлением, но и мощностью. В обоих типах соединения величина всегда суммируется.

В случае, когда элементы монтируются с одной стороны к одному проводнику, а с другой ко второму, соединение называется параллельным. В отличие от предыдущего варианта, где по мере прохождения по цепи электроны сталкивались со все новыми препятствиям, здесь, наоборот, у зарядов появляется больше путей прохода.
Для расчета применяется такая формула:
Получается, что сопротивление в цепи падает, а величина проводимости, напротив, увеличивается обратнопропорционально.
При необходимости электросхема оснащается наборами из последовательных и смешанных вариантов стыковки. Расчет выполняется поэтапно – для каждого участка по отдельности по своей формуле. Затем результаты складываются.


Применение
На практике рассмотренные типы стыковки резисторов применяются в следующих целях:
- Токоограничитель. Элемент ставится в схему, когда требуется конкретная величина тока для работы какого-нибудь устройства заданного номинала, например, лампочки.
- Стягивание и подтягивание. Поддерживают разомкнутое и сомкнутое состояние пусковых устройств, защищают от потери напряжения, когда цепь замкнута, и замыкания, когда разомкнута.
- Делитель напряжения. Используется для отделения части напряжения от исходного значения. Например, если в цепи 20 В, а есть элемент, для которого требуется всего 10 В – то делитель создает для него 10-вольтную ветку.
Важно! Резистор должен подбираться не только по величине сопротивления, но также мощности – она должна соответствовать нагрузке. Превышение параметра может вызвать воспламенение схемы.
Видео описание
Видео-урок о том, как соединяются резисторы:

Параллельное соединение проводников
При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой.
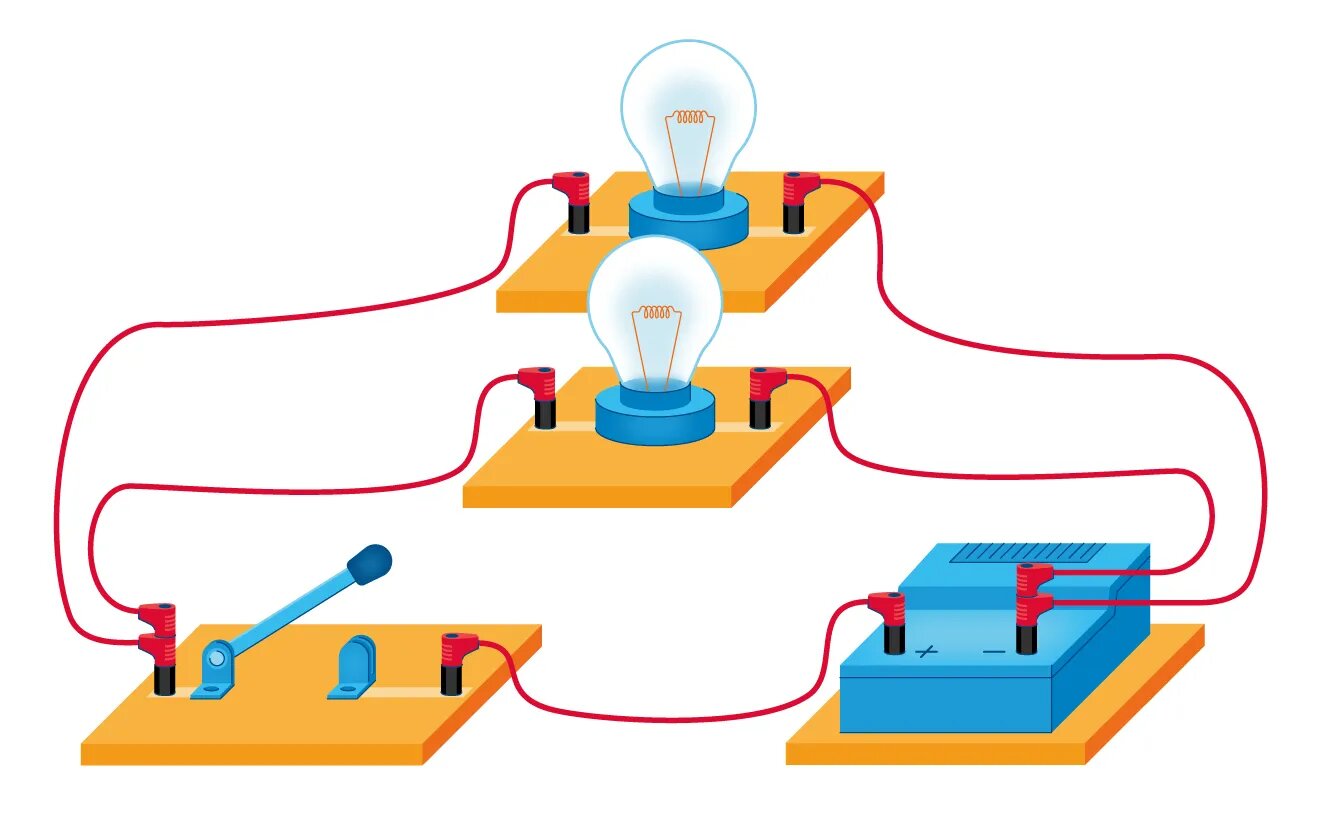
Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату.
Приведем еще несколько примеров применения параллельного способа соединения:
- освещение в больших торговых залах;
- бытовые электроприборы в квартире;
- компьютеры в кабинете информатики;
- вольтметр для измерения напряжения на участке цепи.
Параллельное соединение проводников: формулы
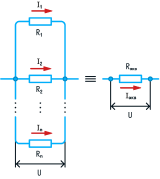
- Напряжение при параллельном соединении в любых частях цепи одинаково: U = U1 = U2 = … = Un. Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении.
- Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках: Iэкв = I1 + I2 + … + In. Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну.
- Общее сопротивление цепи определяется по формуле: 1 / Rэкв = 1 / R1 + 1 / R2 + … + 1 / Rn. Для двух параллельно соединенных проводников формулу можно записать иначе: Rэкв = (R1 · R2) / (R1 + R2).
Если n одинаковых проводников, каждый из которых имеет сопротивление R1, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество:
Вернемся к Анфисе и ее гирлянде. Мы уже разобрались, почему перестали гореть все зеленые лампочки. Пришло время узнать, почему продолжили гореть все остальные. В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.
Пример решения задачи
Два резистора с сопротивлениями 10 Ом и 11 Ом соответственно соединены параллельно и подключены к напряжению 220 В. Чему равна сила тока в неразветвленной части цепи?
Решение.
- Определим общее сопротивление при параллельном соединении проводников: R = (R1 · R2) / (R1 + R2) = (10 · 11) / (10 + 11) = 110 / 21 Ом ≈ 5,24 Ом.
- По закону Ома определим силу тока в цепи: I = U / R = 220 / (110 / 21) = 42 А.
Ответ: сила тока в неразветвленной части цепи равна 42 А.
Выберите идеального репетитора по физике
15 000+ проверенных преподавателей со средним рейтингом 4,8. Учтём ваш график и цель обучения

Смешанное соединение проводников
Зачастую реальные электрические схемы оказываются сложнее, поэтому используют различные комбинации последовательного и параллельного способов соединения. Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.
Алгоритм решения задач со смешанным соединением проводников:
- Прочитать условие задачи, начертить схему электрической цепи, при необходимости пронумеровать проводники.
- Проанализировать схему, т. е. найти участки, где используется только последовательное или только параллельное соединение проводников. Определить сопротивление на этих участках.
- Выяснить вид соединения участков между собой. Найти общее сопротивление всей цепи.
- С помощью закона Ома и законов последовательного и параллельного соединения проводников найти распределения токов и напряжений в цепи.
Пример решения задачи
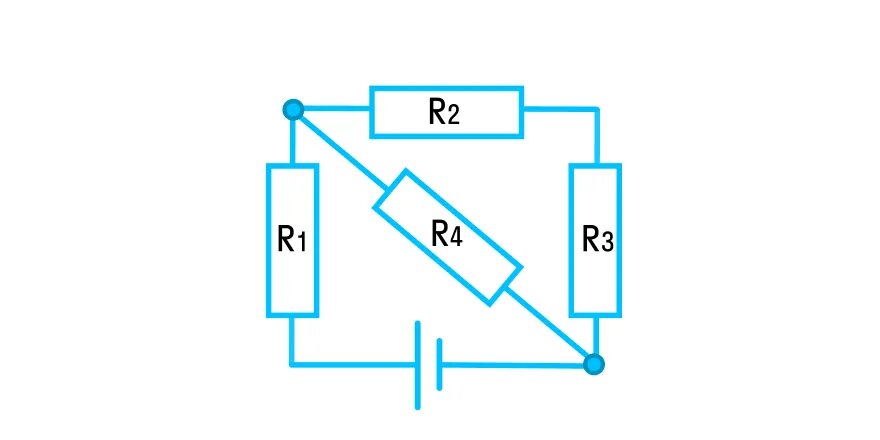
На рисунке показана схема электрической цепи. Сопротивления резисторов одинаковы и равны 12 Ом. Напряжение источника — 100 В. Какова сила тока, протекающего через резистор R4?
Решение.
- Проанализируем данную схему. Резисторы R2 и R3 соединены между собой последовательно, а с резистором R4 — параллельно. Весь этот участок соединен последовательно с источником тока и резистором R1.
- Определим сопротивление последовательно соединенных резисторов R2 и R3: R23 = R2 + R3 = 12 + 12 = 24 Ом.
- Найдем общее сопротивление резистора R4 и участка 2–3, соединенных параллельно: R234 = (R23 · R4) / (R23 + R4) = (24 · 12) / (24 + 12) = 8 Ом.
- Определим общее сопротивление всей цепи как сумму включенных последовательно резистора R1 и участка 2–3–4: Rэкв = R1 + R234 = 12 + 8 = 20 Ом.
- По закону Ома найдем силу тока в неразветвленной части цепи: I = U / Rэкв = 200 / 20 = 5 А.
- По закону Ома определим напряжение на участке, состоящем из резисторов R2, R3, R4: Uэкв1 = I · R234 = 5 · 8 = 40 В.
- Поскольку при параллельном соединении напряжение одинаково, то напряжение на резисторе R4 также равно 40 В. По закону Ома найдем силу тока, протекающего через резистор R4: I4 = Uэкв1 / R4 = 40 / 12 ≈ 3,3 А.
Ответ: через резистор R4 протекает ток силой приблизительно 3,3 А.
Мы разобрали довольно много формул последовательного и параллельного подключения проводников. А запомнить их можно с помощью вот таких схем:
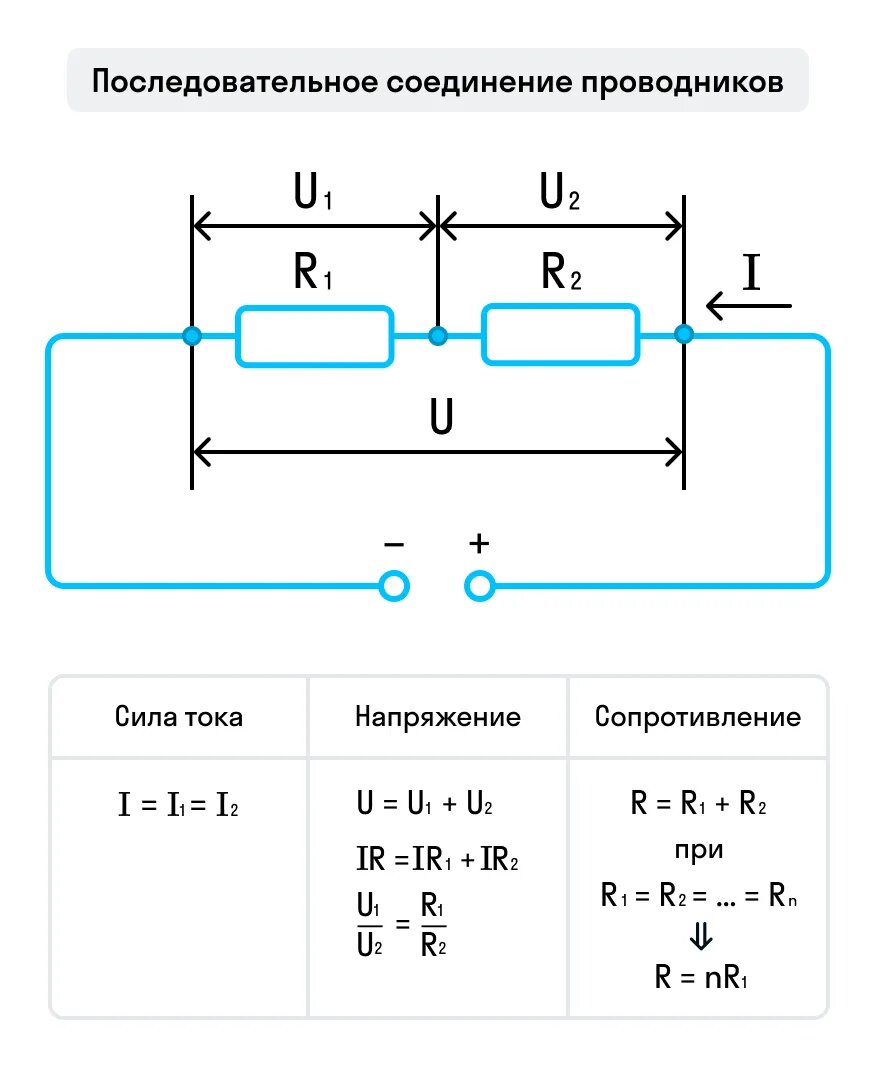
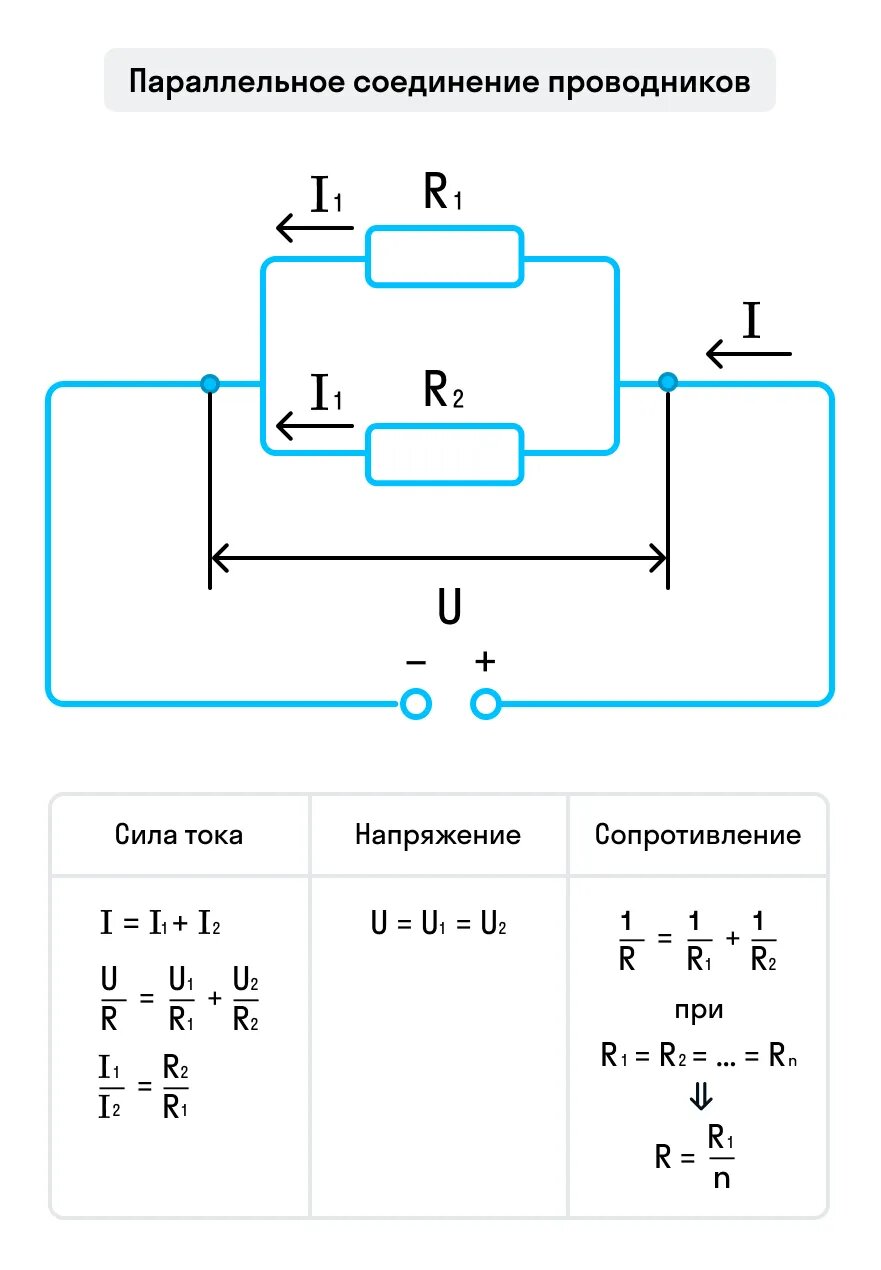
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!
Расчет последовательного и параллельного соединения резисторов — онлайн-калькулятор
Рассчитайте сопротивление при параллельном и последовательном подключении резисторов онлайн — расчет соединения резисторов при помощи калькулятора.
Все калькуляторы
Также можно рассчитать
- Конфигурация
- Расчёт
- Сохранить
- Справка
- Партнерские скидки
- Виджет на сайт
- Комментарии
Запуск приложения
Выберите способ сохранения

Скачать PDF
Скачать расчёт с выбранными параметрами в формате PDF — чертежи + данные.

Поделиться
Поделиться ссылкой на расчёт в Facebook, ВКонтакте, Google+ и т.д.

Сканировать QR-код
Получить ссылку на расчет с параметрами через сканирование QR-кода
Разместите калькулятор у себя на сайте БЕСПЛАТНО
Соединение резисторов последовательным или параллельным способом позволяет получить проводник с определенным номинальным сопротивлением, необходимым для выполнения поставленной задачи. Резисторы, соединенные последовательно, приводят к увеличению общего сопротивления на сумму сопротивлений каждого элемента. Параллельное подключение, наоборот, приводит к уменьшению сопротивления на величину, пропорциональную сумме сопротивлений и количества элементов. Математически это можно представить следующим образом:
При помощи калькулятора соединение резисторов от КАЛК.ПРО можно выполнить расчет сопротивлений при последовательном и параллельном подключении неограниченного количества элементов. Для начала вычисления введите данные сопротивления каждого резистора и их количество, а затем нажмите кнопку «Рассчитать».
Как рассчитать общее сопротивление резисторов?
- Выберите тип соединения (последовательное, параллельное).
- Добавьте необходимое количество элементов.
- Введите сопротивление каждого элемента.
- Нажмите кнопку «Рассчитать»
Смежные нормативные документы:
- ГОСТ 21342.0-75 Резисторы «Общие требования при измерении электрических параметров»
- ГОСТ 28608-90 (МЭК 115-1-82) «Резисторы постоянные для электронной аппаратуры»
- СП 76.13330.2016 «Электротехнические устройства»
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:

Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
![]()
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:

Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:

Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:

Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.

Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.

Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Последовательное и параллельное соединение проводников
В быту и в промышленности в электрическую цепь соединяются сразу несколько потребителей электрической энергии. Различают три вида соединения сопротивлений (резисторов):
- последовательное соединение проводников
- параллельное соединение проводников
- смешанное соединение проводников
Последовательное соединение проводников
Схема соединения выглядит следующим образом:
Рис. (1). Схема № (1)
Обрати внимание!
При последовательном соединении все входящие в него проводники соединяются друг за другом, т.е. конец первого проводника соединяется с началом второго.
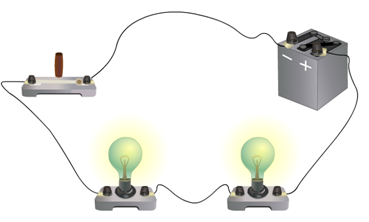
Рис. (2). Две лампы, последовательно
Опыт показывает:
Сила тока в любых частях цепи одна и та же (об этом свидетельствуют показания амперметров): I = I 1 = I 2 .
Если выкрутить одну лампу, то цепь разомкнётся, а другая лампа тоже погаснет.
Опыт показывает следующее:
При последовательном соединении сопротивлений результирующее напряжение равно сумме напряжений на участках: U = U 1 + U 2 .
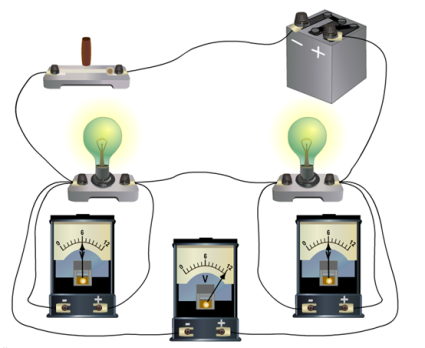
Рис. (3). Напряжение при последовательном соединении
Результирующее сопротивление последовательно соединённых потребителей равно сумме сопротивлений потребителей: R = R 1 + R 2 .
Для проверки данного утверждения можно использовать омметр. При подключении омметра ключ должен быть разомкнут!
Омметр подключают по очереди к каждому потребителю, а потом к обоим одновременно.
Сопротивление цепи (R), состоящей из (n) одинаковых ламп, сопротивлением R 1 каждая, в (n) раз больше сопротивления одной лампы: (R) = R 1 * (n).
Пример 4
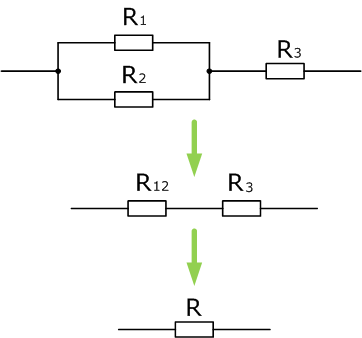
Чтобы рассчитать общее сопротивление смешанного соединения проводников, необходимо для начала найти общее сопротивление резисторов R1 и R2 соединенных параллельно, а затем общее сопротивление, как сумму R12 и R3 соединенных последовательно.
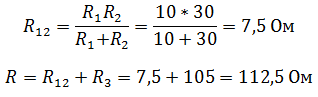
Пример 5
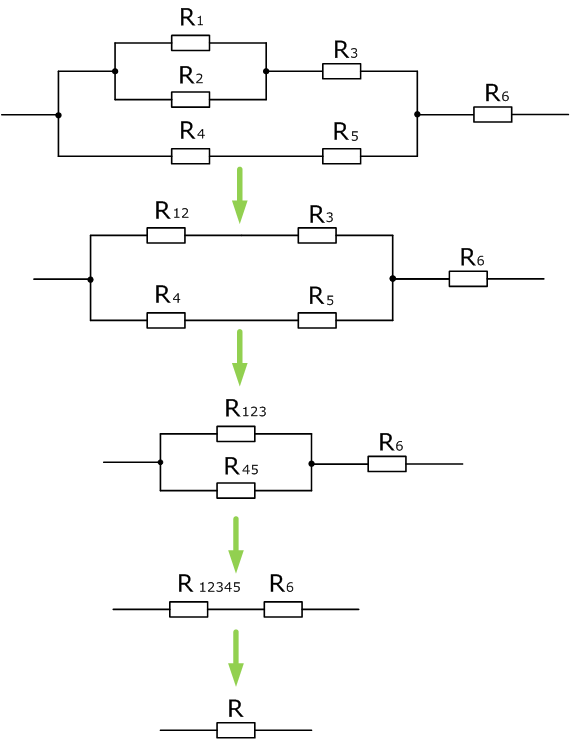
Данная электрическая цепь сложнее, чем предыдущие, но как можно увидеть, она также состоит из последовательно или параллельно соединенных сопротивлений, которые можно постепенно сворачивать, приводя цепь к единственному эквивалентному сопротивлению R.
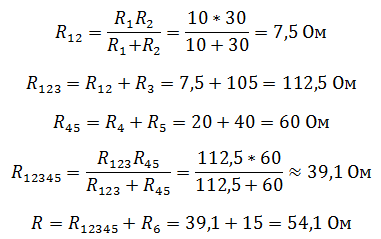
Путем сворачивания цепи с помощью преобразований последовательно и параллельно соединенных проводников, можно максимально упростить для дальнейшего расчета сколь угодно сложную схему. Исключением служат цепи содержащие сопротивления, соединенные по схеме звезда и треугольник.




