Как формулируется закон ома для полной цепи

Содержание

Если изолированный проводник поместить в электрическое поле то на свободные заряды в проводнике будет действовать сила В результате в проводнике возникает кратковременное перемещение свободных зарядов. Этот процесс закончится тогда, когда собственное электрическое поле зарядов, возникших на поверхности проводника, скомпенсирует полностью внешнее поле. Результирующее электростатическое поле внутри проводника будет равно нулю (см. § 1.5).

Однако, в проводниках при определенных условиях может возникнуть непрерывное упорядоченное движение свободных носителей электрического заряда. Такое движение называется электрическим током . За направление электрического тока принято направление движения положительных свободных зарядов. Для существования электрического тока в проводнике необходимо создать в нем электрическое поле.

Количественной мерой электрического тока служит сила тока – скалярная физическая величина, равная отношению заряда Δ, переносимого через поперечное сечение проводника (рис. 1.8.1) за интервал времени Δ, к этому интервалу времени:

Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным .

Рисунок 1.8.1.

Упорядоченное движение электронов в металлическом проводнике и ток . – площадь поперечного сечения проводника, – электрическое поле

В Международной системе единиц СИ сила тока измеряется в амперах (А). Единица измерения тока устанавливается по магнитному взаимодействию двух параллельных проводников с током (см. § 1.16).

Постоянный электрический ток может быть создан только в замкнутой цепи , в которой свободные носители заряда циркулируют по замкнутым траекториям. Электрическое поле в разных точках такой цепи неизменно во времени. Следовательно, электрическое поле в цепи постоянного тока имеет характер замороженного электростатического поля. Но при перемещении электрического заряда в электростатическом поле по замкнутой траектории, работа электрических сил равна нулю (см. § 1.4). Поэтому для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения . Такие устройства называются источниками постоянного тока . Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .

Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.

Урок 256. Закон Ома для полной (замкнутой) цепи.

При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.

Физическая величина, равная отношению работы сторонних сил при перемещении заряда от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):

Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).

При перемещении единичного положительного заряда по замкнутой цепи постоянного тока работа сторонних сил равна сумме ЭДС, действующих в этой цепи, а работа электростатического поля равна нулю.

Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными . Участки, включающие источники тока, называются неоднородными .

При перемещении единичного положительного заряда по некоторому участку цепи работу совершают как электростатические (кулоновские), так и сторонние силы. Работа электростатических сил равна разности потенциалов Δφ12 = φ1 – φ2 между начальной (1) и конечной (2) точками неоднородного участка. Работа сторонних сил равна по определению электродвижущей силе 12, действующей на данном участке. Поэтому полная работа равна

12 = φ1 – φ2 + 12.

Величину 12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:

12 = φ1 – φ2.

Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока , текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника:

где = const.

Величину принято называть электрическим сопротивлением . Проводник, обладающий электрическим сопротивлением, называется резистором . Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.

В СИ единицей электрического сопротивления проводников служит ом (Ом). Сопротивлением в 1 Ом обладает такой участок цепи, в котором при напряжении 1 В возникает ток силой 1 А.

Проводники, подчиняющиеся закону Ома, называются линейными . Графическая зависимость силы тока от напряжения (такие графики называются вольт-амперными характеристиками , сокращенно ВАХ) изображается прямой линией, проходящей через начало координат. Следует отметить, что существует много материалов и устройств, не подчиняющихся закону Ома, например, полупроводниковый диод или газоразрядная лампа. Даже у металлических проводников при токах достаточно большой силы наблюдается отклонение от линейного закона Ома, так как электрическое сопротивление металлических проводников растет с ростом температуры.

Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:

Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи .

На рис. 1.8.2 изображена замкнутая цепь постоянного тока. Участок цепи () является однородным.

Рисунок 1.8.2.

Цепь постоянного тока

Участок () содержит источник тока с ЭДС, равной .

По закону Ома для неоднородного участка,

Сложив оба равенства, получим:

Эта формула выражет закон Ома для полной цепи : сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.

Сопротивление неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока . В этом случае участок () на рис. 1.8.2 является внутренним участком источника. Если точки и замкнуть проводником, сопротивление которого мало по сравнению с внутренним сопротивлением источника ( ток короткого замыкания

Сила тока короткого замыкания – максимальная сила тока, которую можно получить от данного источника с электродвижущей силой и внутренним сопротивлением . У источников с малым внутренним сопротивлением ток короткого замыкания может быть очень велик и вызывать разрушение электрической цепи или источника. Например, у свинцовых аккумуляторов, используемых в автомобилях, сила тока короткого замыкания может составлять несколько сотен ампер. Особенно опасны короткие замыкания в осветительных сетях, питаемых от подстанций (тысячи ампер). Чтобы избежать разрушительного действия таких больших токов, в цепь включаются предохранители или специальные автоматы защиты сетей.

В ряде случаев для предотвращения опасных значений силы тока короткого замыкания к источнику последовательно подсоединяется некоторое внешнее сопротивление. Тогда сопротивление равно сумме внутреннего сопротивления источника и внешнего сопротивления, и при коротком замыкании сила тока не окажется чрезмерно большой.

Если внешняя цепь разомкнута, то , т. е. разность потенциалов на полюсах разомкнутой батареи равна ее ЭДС.

Если внешнее нагрузочное сопротивление включено и через батарею протекает ток , разность потенциалов на ее полюсах становится равной

На рис. 1.8.3 дано схематическое изображение источника постоянного тока с ЭДС равной и внутренним сопротивлением в трех режимах: «холостой ход», работа на нагрузку и режим короткого замыкания (к. з.). Указаны напряженность электрического поля внутри батареи и силы, действующие на положительные заряды: – электрическая сила и – сторонняя сила. В режиме короткого замыкания электрическое поле внутри батареи исчезает.

Рисунок 1.8.3.

Схематическое изображение источника постоянного тока: 1 – батарея разомкнута; 2 – батарея замкнута на внешнее сопротивление ; 3 – режим короткого замыкания

Для измерения напряжений и токов в электрических цепях постоянного тока используются специальные приборы – вольтметры и амперметры .

Вольтметр предназначен для измерения разности потенциалов, приложенной к его клеммам. Он подключается параллельно участку цепи, на котором производится измерение разности потенциалов. Любой вольтметр обладает некоторым внутренним сопротивлением . Для того, чтобы вольтметр не вносил заметного перераспределения токов при подключении к измеряемой цепи, его внутреннее сопротивление должно быть велико по сравнению с сопротивлением того участка цепи, к которому он подключен. Для цепи, изображенной на рис. 1.8.4, это условие записывается в виде:

Это условие означает, что ток , протекающий через вольтметр, много меньше тока , который протекает по тестируемому участку цепи.

Поскольку внутри вольтметра не действуют сторонние силы, разность потенциалов на его клеммах совпадает по определению с напряжением. Поэтому можно говорить, что вольтметр измеряет напряжение.

Амперметр предназначен для измерения силы тока в цепи. Амперметр включается последовательно в разрыв электрической цепи, чтобы через него проходил весь измеряемый ток. Амперметр также обладает некоторым внутренним сопротивлением A. В отличие от вольтметра, внутреннее сопротивление амперметра должно быть достаточно малым по сравнению с полным сопротивлением всей цепи. Для цепи на рис. 1.8.4 сопротивление амперметра должно удовлетворять условию

чтобы при включении амперметра ток в цепи не изменялся.

Измерительные приборы – вольтметры и амперметры – бывают двух видов: стрелочные (аналоговые) и цифровые. Цифровые электроизмерительные приборы представляют собой сложные электронные устройства. Обычно цифровые приборы обеспечивают более высокую точность измерений.

Рисунок 1.8.4.

Формулировка и объяснение закона Ома

Немец Георг Ом изучал фичи электричества в 19 веке, и стал таким великим физиком, что в честь него теперь законы называют. И не зря. Это мы уже хорошо знакомы с ним и его возможностями, потому что он есть в каждом доме. А тогда люди только начали изучать движение частиц, и не все было так очевидно. Поэтому наш ученый долго следил за потоком частиц и вывел закономерности.

В такой форме закон Ома дошел до наших дней: сила тока через участок цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.

Это значит, что здесь линейная зависимость: при увеличении напряжения, увеличится сила потока и наоборот.

Формула: I = U / R,

где I — сила тока, U — напряжение, R — сопротивление.

Это правило может применяться далеко не для всех условий. Оно характерно для постоянного тока, для переменного используются другие понятия. Но в ОГЭ и ЕГЭ тебе точно встретятся задачи, для решения которых придется вспомнить об этой зависимости.

Закон Ома для участка цепи

Проверим твою внимательность: заметил, что в самом определении закона Ома используется термин «участок цепи»?

Определние, которое мы приводили выше, и является законом Ома для участка цепи.

Что такое этот загадочный участок? Это часть электросхемы, которая содержит определенный набор элементов. В этой части мы и будем проводить наши изменения и вычисления, не обращая внимания на другие условия.

Когда мы имеем дело с таким отдельно взятым участком, смело можем использовать выражение, которое, надеемся, ты запомнил.

Закон Ома для полной цепи

Возьмем источник постоянного тока, состоящий из сосуда с серной кислотой и помещёнными в него цинковым и угольным электродами. Цинк отдаёт в кислоту двухвалентные ионы, становясь согласно закону сохранения заряда отрицательно заряженным. Для рассмотрения закона Ома для полной цепи на участке между электродами помещается резистор, замыкающий цепь, что приводит к появлению постоянного электрического тока – избыток электронов цинка начнёт движение в угольный электрод. В ходе химической реакции совершается работа А по переносу заряда q. Её целесообразно выразить через ЭДС:

Кроме того, по закону сохранения энергии работа расходуется на выделение тепла Q в нагрузке и в самом источнике:

Количество теплоты согласно закону Джоуля-Ленца для источника и нагрузки:

Q = I²• r • t, где r – сопротивление источника
и
Q = I²• R • t, где R – сопротивление нагрузки.

Выразим количество электричества (заряд) через силу тока:

Для вывода закона Ома продолжаем преобразования и получаем ЭДС для полной цепи:

ε • I • t = I²• r • t + I²• R • t
⇓
ε = I•r + I•R – из этого выражения выводится формула закона Ома для полной цепи:

Классическая формулировка закона Ома для полной цепи: сила тока полной цепи прямопропорциональна ЭДС источника и обратноспропорциональна полному сопротивлению цепи.

Обычно сопротивление источника значительно ниже сопротивления нагрузки: R ≫ r. В таких случаях ε ≈ U, а формула принимает вид уравнения закона Ома для участка цепи:

Примечательно, что изначально принятые Георгом Омом символы отличаются от используемых сегодня.

Закон Ома для переменного тока.

В случае токов, подчиняющихся гармоническому закону, нагрузка проявляет ряд особенностей. В реальной цепи наравне с активной (резистивной) нагрузкой в той или иной степени обязательно присутствуют ёмкость и индуктивность, создавая колебательный контур. Эти элементы представляют собой реактивную составляющую нагрузки, расчёт которой несколько сложнее.

Возьмем последовательную цепь из резистора, конденсатора и катушки в установившемся режиме, питающуюся от источника ЭДС с пренебрежимым сопротивлением (при этом e ≈ U), соединённую идеальными проводниками:

За основу векторной диаграммы возьмем ток, так как он одинаковый на всех элементах схемы. Напряжение на резисторе совпадает по направлению с током. В катушке появляется ЭДС индукции, противодействующая изменению напряжения, а в конденсаторе напряжение препятствует току, соответственно, фазы колебаний в них отличаются: в катушке напряжение опережает ток, в конденсаторе зависимость обратная:

где ω – радиальная частота, равняющаяся 2πf, т. е. 100π при 50 Гц.

Результирующее напряжение согласно параллелограмму сил:

Емкостное сопротивление обозначается XС, а индуктивное XL. Полное сопротивление обозначается Z и называется импедансом. Для простоты его называют сопротивлением, учитывающим частоту.

Выразим отсюда полное сопротивление, т. е. сопротивление, определяющее активно-реактивный характер нагрузки:

Имея все параметры рассматриваемой модели в установившемся режиме можно записать закон Ома для полной цепи переменного тока в установившемся режиме:

Вывод формул закона Ома

Вывод формулы закона Ома для участка цепи можно провести на основе закона Джоуля-Ленца. Этот закон гласит, что количество теплоты Q, выделяющееся на участке цепи, пропорционально квадрату силы тока I, сопротивлению участка R и времени прохождения тока t:

С другой стороны, по закону сохранения энергии выделившаяся на участке теплота Q равна работе A тока на преодоление напряжения U:

Приравнивая два выражения для Q и решая полученное уравнение относительно I, получаем формулу закона Ома для участка цепи:

Аналогично можно вывести формулу закона Ома для полной цепи, основываясь на законе Джоуля-Ленца для полной цепи:

Решая это уравнение относительно I, окончательно получаем:

Таким образом, используя более общие законы физики, можно строго математически получить основные формулы закона Ома, выражающие связь между током, напряжением и сопротивлением.

Графическая интерпретация закона Ома

Закон Ома для участка цепи можно проиллюстрировать с помощью так называемого треугольника Ома:

Этот треугольник наглядно демонстрирует связь между током I, напряжением U и сопротивлением R:

ток I пропорционален напряжению U и обратно пропорционален R;
если U растёт, то растёт и I;
если R растёт, то I уменьшается.

Треугольник Ома наглядно демонстрирует качественную зависимость между величинами, о которой говорит закон Ома. Это помогает лучше понять физический смысл закона.

Далее рассмотрим примеры применения закона Ома для расчёта электрических цепей.

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

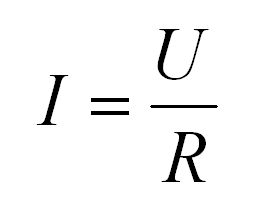
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

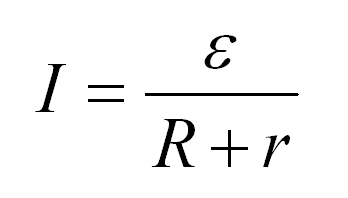
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

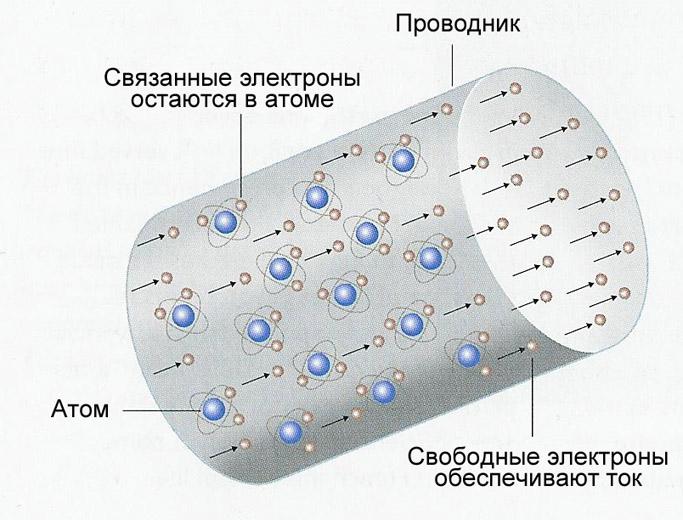
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Мы поможем сдать на отлично и без пересдач

Контрольная работа от 1 дня / от 120 р. Узнать стоимость
Дипломная работа от 7 дней / от 9540 р. Узнать стоимость
Курсовая работа от 5 дней / от 2160 р. Узнать стоимость
Реферат от 1 дня / от 840 р. Узнать стоимость

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Отдельный участок и полная электрическая цепь

Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.

Расчет тока участка электрической схемы

Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.

Поэтому расчетная формула, в данном случае, выглядит просто:

I = U/ R,

Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.

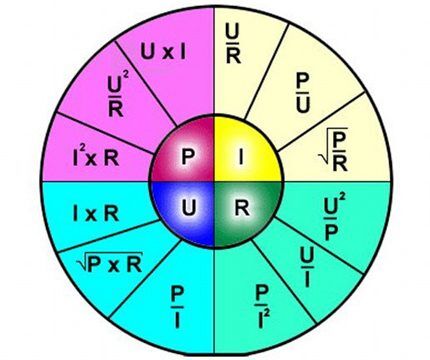
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления

Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.

Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.

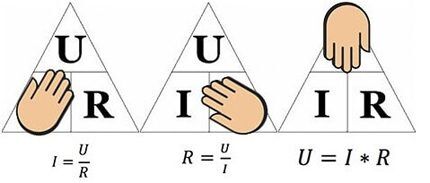
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление

Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.

Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).

Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.

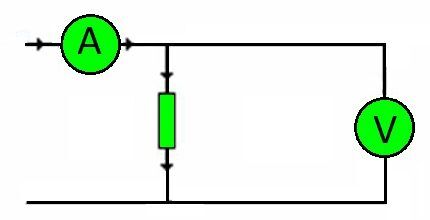
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.

Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.

Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.

У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.

Вариант расчета для полной цепи

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.

Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.

Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

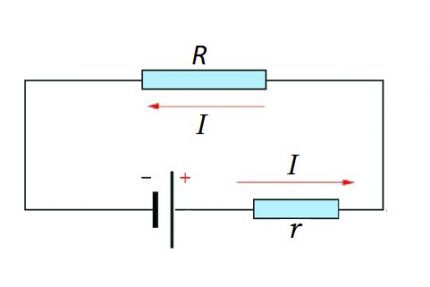
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.

Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Рассмотрение действия закона к переменной величине

Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).

Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока

Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.

Расчёт подобных явлений ведётся при помощи формулы:

Z = U / I или Z = R + J * (XL — XC)

где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

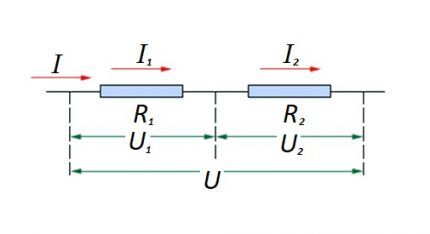
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

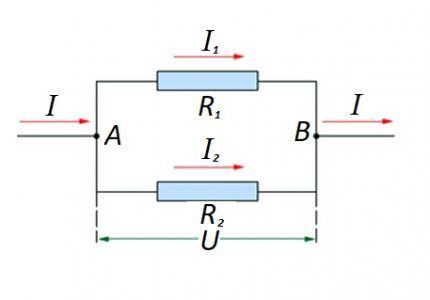
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Пример

Представим схему с источником энергии и с лампочкой. И следуем закону Ома.

Если мы увеличим напряжение, то лампочка будет светиться ярче, ведь сила потока зарядов увеличится. Если же у нас будет лампочка с большим сопротивлением, то она будет светиться слабее.