Системы счисления – одна из самых главных основ информатики. Практически ни в одной школе и ни в одном университете не пропускают данную тему, но зачастую именно с переводом шестнадцатеричной системы у многих возникают проблемы, хотя это не такая уж сложная задача, и её перевод практически не отличается от других систем счисления.
Давайте рассмотрим эту систему поподробнее.
Для чего нужна шестнадцатеричная система
Итак, шестнадцатеричная система счисления, как следует из названия, имеет в своём основании число 16. Почему так? Дело в том, что единица информации в информатике – это бит. Восемь бит образуют байт. Также информационной среде существует такое понятие, как машинное слово – это минимальная единица данных, представляющая собой шестнадцать бит, то есть два байта. Считается, что машинное слово – это минимальная величина разрядности регистров процессора, при которой можно работать с ЭВМ.
Так вот, как мы знаем, компьютер работает на двоичном коде. Однако, если Вы когда-нибудь переводили числа из двоичной системы в десятичную, то замечали, что в ней бывает довольно много разрядов, особенно при переводе больших чисел, например, перевод числа 5132 в двоичной системе будет записано так:

Как можно увидеть, при переводе в двоичную систему этого числа у нас получилось аж 13 разрядов (с 0 до 12). Довольно муторно, а главное, занимает много места на письме и отнимает много времени для перевода.
Именно для этого придумали восьмеричную и шестнадцатеричную системы счисления, для этого придумали и байты. Эти системы помогают сократить затраты на перевод чисел и привести их к более приятному визуальному виду.
Если перевести то же число 5132 в восьмеричную систему счисления, то получится «более сокращённая версия» двоичного кода:
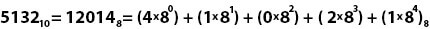
Как мы видим, количество символов сократилось, так как разрядность уменьшилась до 5 (с 0 до 4).
Как можно уже понять, шестнадцатеричная система ещё сильнее сокращает разрядность (с 0 до 3) и ещё сильнее сжимает на письме переведённое число:
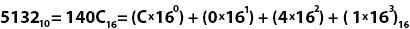
Человеку такой вид записи в любом случае удобнее, чем бесконечные нули и единицы.
Таким образом, шестнадцатеричная система используется довольно широко в современных информационных системах. Например, при помощи неё указываются коды цветовых схем, данная система используется для записи кодов ошибок, а также для программирования на языках низкого уровня типа Ассемблера, шестнадцатеричную систему зачастую используют для предоставления данных и адресов в малоразрядных ЭВМ.
Основы #HEX для хакеров
Двоичная система счисления — основа мироздания.
Вы помните Даосский символ Инь и Янь? Он состоит из двух цветов, из двух понятий: чёрного и белого, мужского и женского, единицы и нуля. Согласно Даосской философии весь мир сформирован именно с помощью двух противоположных
и вместе с тем неразделимых понятий. Просто поражает гениальность древних мудрецов. С помощью единиц и нулей человек создаёт множество цифровых миров. Год от года они становятся всё более реалистичными. Интересно, догадывается
ли герой компьютерной игры, что весь его мир состоит всего из двух цифр или это только мы такие прозорливые :)?
Десятичная система счисления.
Двоичная система счисления аппретирует только двумя цифрами: Единицей
и Нулём (Инь и Янь). Привычная для нас система счисления — десятеричная. Если все цифры до десяти состоят из различных одиночных символов (от нуля до девятки), то десять отображается уже двумя символами — единицей и нулём, расположенных
в определённой последовательности (10 — единица перед нулём).
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными.
В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F. При переводе в десятичную систему буквы заменяются числами 10, 11, 12, 13, 14, 15 соответственно.
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
В случае обратного перевода шестнадцатеричные цифры заменяются соответствующими четырехразрядными двоичными числами.
Перевод из шестнадцатеричной системы счисления в десятичную выполняется аналогично переводу из двоичной и восьмеричной. Только здесь в качестве основания степени выступает число 16, а цифры от A до F заменяются десятичными числами от 10 до 15.
4C5 = 4 * 16 2 + 12 * 16 1 + 5 * 16 0 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи, – это число FF.
FF16 = 15 * 16 1 + 15 * 16 0 = 240 + 15 = 25510
В двоичном представлении FF будет выглядеть как восьмиразрядное число 11111111. Наименьшей рабочей ячейкой компьютерной памяти является байт, который состоит из 8-ми битов. Каждый бит может быть в двух состояниях – «включено» и «выключено». Одному из них сопоставляют ноль, другому – единицу.
Следовательно, в одном байте можно сохранить любое двоичное число в диапазоне от 00000000 до 11111111. В десятичном представлении это числа от 0 до 255. В шестнадцатеричном – от 0 до FF. С помощью шестнадцатеричной системы счисления удобно кратко, с помощью двух цифр-знаков, записывать значения байтов. Например, 0E или F5.
Несмотря на то, что 25510 – это максимальное значение, которое можно сохранить в байте, состояний у 8-ми битного байта 256, так как одно из них отводится под хранение нуля. Количество возможных состояний ячейки памяти вычисляется по формуле 2 n , где n – количество составляющих ее бит. В случае восьми бит получаем:
Системы счисления, перевод систем счисления
Всем доброго дня. При работе с микроконтроллерами и цифровой схемотехникой иногда нужно представить число или записать в какой-то регистр нужное значение, но значение нужно представить например в двоичном виде, для этого нужно уметь преобразовывать числа в разные представления. На заре развития компьютеров и электроники данными операциями приходилось заниматься этим в «ручную». Но на сегодняшний день все намного проще, и сегодня мы рассмотрим несколько способов перевода чисел в другие системы счисления.
Система счисления — это метод представления чисел путем записи их в какими то знаками. Обычно все системы исчисления имеют общепринятые значения для каждого числа, например в двоичной системе цифра 2 выглядит как «00000011».
Основные системы счисления
- десятичная система счисления
- двоичная система счисления
- восьмеричная система счисления
- Шестнадцатеричная система счисления
Десятичная система счисления — это привычная для нас система записи чисел, в которой числа формируется из 10 цифр (от 0 до 9).
Двоичная система счисления — это система в котором числа представляется при помощи нулей «0» и единиц «1». Если число больше 2 для записи используется определенная последовательность, например число 50 записывается как «110010». Двоичная система повсеместно используется в электронике, это связано с тем что большинство цифровых элементов имеют два состояния, а такие устройства как триггеры, регистры, счетчики являются двоичными.
Восьмеричная система счисления — система исчисления где числа представляются с помощью цифр от 0 до 7 (т.е. восьми цифр). Такая система нашла применения для установки прав доступа к файлам в операционной системе линукс.
Шестнадцатеричная система счисления — система счисления в котором число представляется при помощи цифр от 0 до 9 и латинских букв от A до F. Данное представление получило распространение в языках программирования таких как С и помогает сделать запись байта более коротким.
| Десятичная | Двоичная | Восьмеричная | шеснадцатиричная |
| 1 | 1 | 1 | 1 |
| 5 | 101 | 5 | 5 |
| 12 | 1100 | 14 | С |
| 25 | 100101 | 45 | 25 |
| 50 | 110010 | 62 | 32 |
| 75 | 1001011 | 113 | 4B |
| 100 | 1100100 | 144 | 64 |
| 255 | 11111111 | 377 | FF |
Перевод чисел в разлиные системы счисления
На сегодняшний день перевести число в другую систему счисления не представляет особого труда, можно воспользоваться специальными онлайн сервисами, но если нет рядом интернета или просто не хочется заходить в интернет можно воспользоваться калькулятором который есть во всех операционных системах семейства Windows. Думаю много кто и так знает про такую возможность, но все равно опишу чуть подробнее.
Найти калькулятор можно в «Меню пуск — Все программы — стандартные — Калькулятор» или запустить через «Выполнить» (Лично для меня так быстрее), нажимаем комбинацию клавиш «Ctrl + R» в появившемся окне пишем «calc» и нажимаем ОК.
После чего запустится и сам калькулятор, но обычно он запускается в простом режиме нам нужно переключить его в другой режим для работы, для это переходим в меню «Вид» и выбрать режим «программист». Там же можно выбрать «преобразование единиц» но это не обязательно.
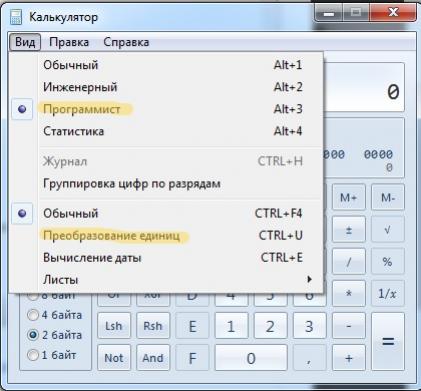
Собственно после этих действий можно заниматься переводом чисел. Немного подробнее про расположения элементов.
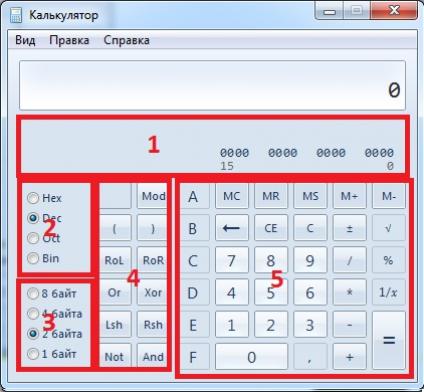
- Панель вывода результата
- Панель выбора системы счисления
- Панель выбора количества байт
- Панель клавиш логических операций
- панель клавиш ввода чисел
Обозначение систем счисления в калькуляторе:
- Dec — десятичная система счисления
- Oct — восьмеричная система счисления
- Hex — шестнадцатеричная система счисления
- Bin — двоичная система счисления
Работает все да воли просто и особого пояснения не требует. Сначала мы выбираем исходную систему исчисления, после чего вводим нужное число и переключаем на нужную систему счисление и калькулятор отобразит число уже в другой системе. Если число не очень большое можно переключить размер на два байта.
Обозначение Логических операция в калькуляторе:
- Or — логическое ИЛИ
- Xor — исключающее ИЛИ
- Not — логическое НЕ
- And — логическое И
- Lsh — сдвиг в лево
- Rsh — сдвиг в право
Работать с логическими операциями тоже не сложно, набираем первое число выбираем нужную операцию и вводим второе число.
Арифметические действия в шестнадцатеричной системе счисления
Сложение и вычитание
Операции сложения и вычитания удобно выполнять с использованием таблицы сложения шестнадцатеричных чисел. И сложение или вычитание выполняются поразрядно, начиная с младшего разряда.

Если при сложении двух чисел одинакового разряда получается двузначное число, то значение его старшего разряда (единицу) добавляют в старший разряд.
Например, 1F + 2D = 4C.
Сначала складываются значения младших разрядов F + D. По таблице получается двузначное число1С, единицу старшего разряда которого переносим и добавляем к сумме следующих по величине разрядов суммируемых шестнадцатеричных чисел.
Сумма цифр старших разрядов 1 + 2 равна 3 и еще прибавляется переносимая единица, то есть получается в сумме 4.
Таким образом, получается число 4C.
При выполнении вычитания часто возникает ситуация, когда необходимо выполнять заем из старшего разряда, если уменьшаемое конкретного разряда меньше вычитаемого. Тогда занимается единица из старшего разряда. Значение разности смотрится по таблице.
Например, 2D – 1F = E.
Сначала находят разность цифр младших разрядов, то есть D – F (в десятичном представлении 13-15). Уменьшаемое меньше вычитаемого, поэтому происходит заем единицы из старшего разряда исходного числа. То есть вычисляют разность 1D – F = E.
После выполненных манипуляций с младшими разрядами переходят к следующим по величине. В текущем примере следует вычислить 2 – 1. Но ранее произошел заем единицы и в старшем разряде уменьшаемого остается не 2, а 1. Поэтому вычисляется разность 1 – 1 = 0.
Умножение и деление
Умножать и делить числа в шестнадцатеричной системе следует также поразрядно. При вычислениях удобно пользоваться таблицей умножения шестнадцатеричной системы счисления.
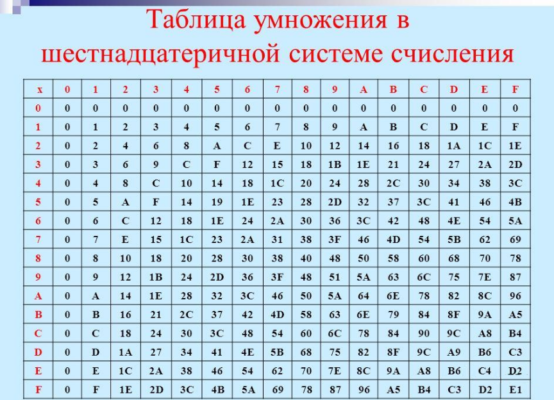
Например, 1С * 2 = 38. Используя распределительный закон умножения: (10 + С) * 2 = 10 * 2 + С * 2 = 20 + 18 = 38
Операция деления также выполняется столбиком с использованием таблицы умножения: 1С / 2 = Е. В строке таблицы для числа 2, то есть делителя, находится значение 1С (делимое) и пересечение этой строки и столбца, где расположено 1С даст значение частного от деления числа, то есть Е.
Общие сведения
Система счисления — метод символьного типа для записи чисел с помощью определенных знаков. Последние записываются посредством чисел и цифр. Однако не все понимают логического смысла последних терминов. Числом называется некоторая абстрактное значение, характеризующее количественные характеристики какой-либо величины, явления или процесса. Цифра является знаком, который необходим для записи числа. Цифры бывают 2 видов: арабскими и римскими. Первые являются самыми распространенными. Они представлены знаковым интервалом от 0 до 9. Чисел больше, и поэтому используется набор цифр. Для этого и были придуманы системы исчисления. Они делятся на четыре группы:

- Позиционные.
- Непозиционные.
- Смешанные.
- Унарные.
К первой группе относятся все разрядные системы, в которых положение и порядок знака играет важную роль. От этого зависит значение величины. Если изменить положение цифр, то число изменится.
Во втором случае простым примером является массив данных с параметром «ключ — значение». Например, массив ассоциативного типа состоит из 3 элементов: ‘login’ -> ‘Ivan10’, ‘pass’ -> ‘12345’ и ‘name’ -> ‘Иван’. В этом случае данные можно менять местами, поскольку логика сохранится.
Смешанной является система, в которой присутствуют данные позиционной и непозиционной групп.Простой пример — деньги. Существуют два типа денежных знаков: монеты и купюры. Например, техника стоит 5250 рублей 50 копеек.
Для получения данной суммы следует использовать некоторое количество купюр и монет: 5250,50 = (5000 + 200 + 50) рублей + 50 копеек.
Унарной называется единичная система с одной цифрой. Последняя может быть представлена в виде 1, черты, креста и любого целого значения. Иными словами, каждый знак соответствует 1. Например, запись «1111111» эквивалентна «|||||||». Если расшифровать ее, то получится число 7. В книге Даниэля Дефо «Робинзон Крузо» герой применял данную систему для подсчета дней, проведенных на острове. Детей обучают математике на начальном уровне с помощью счетных палочек. Если вспомнить историю, то древние люди тоже пользовались унарным счислением.
Позиционные системы в программировании
Наиболее востребованными в IT-сфере являются двоичный и шестнадцатеричный коды. Они применяются для перевода десятичной системы счисления, которая понятна человеку, в машинный язык. Двоичная состоит из двух переменных, которые принимают единичное (1) или нулевое (0) значения. Это очень просто реализовать в электронике и микросхемотехнике.

Микропроцессор персонального компьютера является микросхемой. Она состоит из множества транзисторов, способных кодировать 0 и 1. Схему соединения полупроводниковых приборов составляют так, чтобы они имели два состояния (открыт и закрыт). Кроме того, реализация двоичной системы может быть выполнена в любом устройстве, которое потребляет электрический ток. Наличие кодируется как 1, а отсутствие — 0.
Берутся также некоторые физические процессы: наличие света, сопротивления, намагниченности и так далее. С системой можно связать разные величины, которые имеют два состояния. Новичкам рекомендуется сначала полностью освоить перевод из десятичной системы счисления в двоичную и обратно. После этого следует приступить к изучению шестнадцатеричного кода, расшифровка которого существенно отличается.
Преобразование шестнадцатеричного числа в десятичное
Переведем шестнадцатиричное число 2DB16 в десятичное (рисунок 3).
В верхней строке указаны веса первых трех разрядов: 256, 16 и 1.
- В шестнадцатеричном числе на рисунке 3 имеется одиннадцать единиц в первом разряде.
- В разряде с весом 16 стоит символ D, что соответствует числу 13. Умножая его на вес разряда, получается число 208.
- Двойка в разряде с весом 256 дает число 512.
- Суммируя значения 11 + 208 + 512, получаем число 73110.
| Вес разряда | 256 | 16 | 1 | |
| Шестнадцатеричное число | 2 | D | B16 | |
| ↓ | ↓ | ↓ | ↓ | |
| ↓ | 256×2=512 | 16×13=208 | 1×11=11 | |
| Десятичное число | 512 | +208 | +11 | =73110 |
Преобразование десятичного числа в шестнадцатеричное
Теперь рассмотрим обратное преобразование десятичного числа 47 в его шестнадцатеричную форму.
На рисунке 4 показана процедура последовательных делений на 16.
- Первое деление числа 47 на 16 дает частное 2 и остаток 15. Этот остаток 15 (то есть число F в шестнадцатеричной системе) является младшим разрядом (крайний правый символ) искомого шестнадцатеричного числа.
- Частное (в данном случае 2) надо принять далее в качестве делимого и снова разделить его на 16. В результате получится частное 0 с остатком 2. Эта двойка является следующим разрядом нашего шестнадцатеричного числа.
- На этом процесс преобразования заканчивается, так как получилось частное, равное 0.
С помощью процедуры последовательного деления на 16 мы преобразовали число 4710 в эквивалентное ему шестнадцатеричное число 2F16.
| 4710 | ÷16 | =2 | с остатком | 15 (F16) | |
| 2 | ÷16 | =0 | с остатком | 2 | |
| 4710 = 2F16 | |||||
Заметка
Здесь можно посмотреть, как перевести двоичные числа в десятичные и наоборот. Для быстрого преобразования можно воспользоваться онлайн-калькулятором.