Емкостное сопротивление колебательного контура может быть определено выражением

Содержание

Емкостное сопротивление — это сопротивление конденсатора переменному току. Для постоянного тока, сопротивление конденсатора равно бесконечности, в реальности сопротивлению утечки (диэлектрика).

Онлайн калькулятор выше, позволяет найти:
— Емкостное сопротивление X через частоту f и емкость C по формуле X = frac <2*pi*f*C>;
— Частоту f через емкостное сопротивление X и емкость С по формуле f = frac <2*pi*X*C>;
— Емкость С через частоту f и емкостное сопротивление X по формуле C = frac <2*pi*f*X>.

Емкостное сопротивление — это сопротивление, которое проявляется в электрических цепях, содержащих емкость. Емкость — это физическая величина, которая характеризует способность электрической цепи хранить электрический заряд.

При подключении емкости к источнику постоянного тока, заряды начинают накапливаться на обкладках емкости, пока электрическое поле между ними не станет достаточно сильным, чтобы противодействовать дальнейшему накоплению зарядов. При этом в цепи устанавливается постоянное напряжение, равное напряжению источника.

При подключении емкости к источнику переменного тока, заряды начинают накапливаться и сливаться на обкладках емкости, в зависимости от направления тока. Это приводит к тому, что переменный ток в емкостной цепи опережает по фазе напряжение в цепи.

Математически это выражается формулой X = frac <2*pi*f*C>, где X — емкостное сопротивление, f — частота переменного тока, C — емкость. Емкостное сопротивление измеряется в омах.

Емкостное сопротивление влияет на электрические цепи, содержащие емкость, и может приводить к изменению амплитуды и фазы тока и напряжения в цепи. Это может приводить к нежелательным эффектам, таким как генерация помех и шума в электрических устройствах.

Одним из способов уменьшения влияния емкостного сопротивления в цепи является использование компенсирующих индуктивностей. Компенсирующая индуктивность подключается последовательно к емкости и создает магнитное поле, которое компенсирует электрическое поле, создаваемое емкостью. Таким образом, компенсирующая индуктивность позволяет уменьшить емкостное сопротивление в цепи и улучшить ее электрические характеристики.

Емкостное сопротивление также играет важную роль в электронных устройствах, таких как фильтры, генераторы синусоидального сигнала и широкополосные усилители. В фильтрах емкость используется для подавления определенных частот сигнала, а в генераторах синусоидального сигнала — для создания колебаний на определенной частоте.

В заключение, емкостное сопротивление — это сопротивление, которое проявляется в электрических цепях, содержащих емкость. Емкостное сопротивление может приводить к изменению амплитуды и фазы тока и напряжения в цепи и может быть уменьшено с помощью компенсирующих индуктивностей. Емкость также используется в различных электронных устройствах, таких как фильтры и генераторы синусоидального сигнала, для подавления или создания определенных частот сигнала. Понимание емкостного сопротивления и его влияния на электрические цепи является важным для разработки эффективных и надежных электронных устройств.

Колебательный контур.Полное сопротивление.

Понравилась страница?
Добавить в закладки
Или поделиться!

Емкостное сопротивление колебательного контура может быть определено выражением

Опубликовано 12.06.2017 по предмету Физика от Гость >> Оцени ответ

Алгебра
Математика
Русский язык
Українська мова
Информатика
Геометрия
Химия
Физика
Экономика
Право
Английский язык
География
Биология
Другие предметы
Обществознание
История
Литература
Українська література
Беларуская мова
Қазақ тiлi

Тема занятия 5: Колебательный контур.

Колебательный контур называется идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.

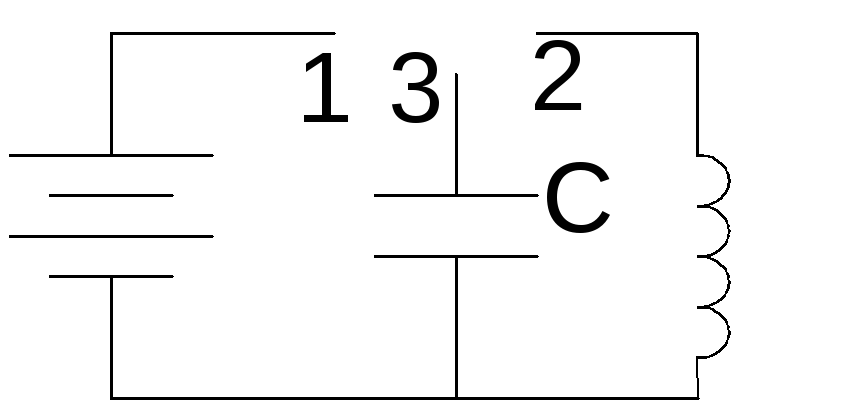
Рассмотрим физические процессы в следующей цепи:

1 Ключ стоит в положении 1. Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,

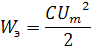
т.е.конденсатор становится источником электрической энергии.

2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.

Ток в цепи достигает максимального значения(точка 1). Напряжение на обкладках конденсатора уменьшается до нуля.

В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся , то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).

Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.

Получившиеся колебания называются свободнымиилисобственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.

Определим угловую частоту свободных колебаний:

Используем равенство энергий электрического и магнитного полей

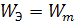
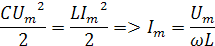
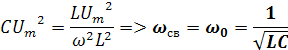
,где ώ угловая частота свободных колебаний.

[ ώ ]=1/с

f0=ώ/2π [Гц].

Период свободных колебаний Т0=1/f.

Частоту свободных колебаний называют частотой собственных колебаний контура.

Из выражения: ώ²LC=1получимώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.

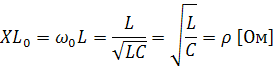
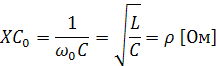
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.

Характеристическое сопротивление вычисляется по формулам:

2 Реальный колебательный контур

Реальный колебательный контур обладает активным сопротивлением, поэтому при воздействии в контуре свободных колебаний энергия предварительно заряженного конденсатора постепенно тратится, преобразуясь в тепловую.

Свободные колебания в контуре являются затухающими, так как в каждый период энергия уменьшается и амплитуда колебаний в каждый период будет уменьшаться.

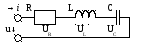
Рисунок — реальный колебательный контур.

Угловая частота свободных колебаний в реальном колебательном контуре :

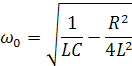
Если R=2… , то угловая частота равна нулю, следовательно свободные колебания в контуре не возникнут.

Таким образом колебательным контуромназывается электрическая цепь состоящая из индуктивности и емкости и обладающая малым активным сопротивлением, меньшим удвоенного характеристического сопротивления, что обеспечивает обмен энергией между индуктивностью и емкостью.

В реальном колебательном контуре свободные колебания затухают тем быстрее, чем больше активное сопротивление.

Для характеристики интенсивности затухания свободных колебаний используется понятие «затухание контура» — отношение активного сопротивления к характеристическому.

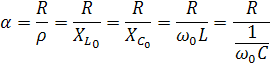
На практике используют величину, обратную затуханию – добротность контура.

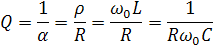
Для получения незатухающих колебаний в реальном колебательном контуре необходимо в течение каждого периода колебаний пополнять электрическую энергию на активном сопротивлении контура в такт с частотой собственных колебаний. Это осуществляется с помощью генератора.

Если подключить колебательный контур к генератору переменного тока, частота которого отличается от частоты свободных колебаний контура, то в цепи протекает ток с частотой равной частоте напряжения генератора. Эти колебания называют вынужденным.

Если частота генератора отличается от собственной частоты контура, то такой колебательный контур является ненастроенным относительно частоты внешнего воздействия, если же частоты совпадают, то настроенным.

Задача: Определить индуктивность , угловую частоту контура, характеристическое сопротивление, если емкость колебательного контура 100 пФ, частота свободных колебаний 1,59 МГц.

Тестовые задания:

Добротность колебательного контура определяется по формуле:

Отношение активного сопротивления к характеристическому
Величина обратная затуханию

непрерывные колебания энергии между электрическим и магнитным полями
колебания, амплитуда которых в каждый период времени уменьшается

Тема занятия 8: РЕЗОНАНС НАПРЯЖЕНИЙ Резонанс напряжений – явление возрастания напряжений на реактивных элементах, превышающих напряжение на зажимах цепи при максимальном токе в цепи, которое совпадает по фазе с входным напряжением. 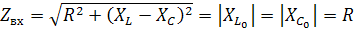Условия возникновения резонанса:

Последовательное соединение LиCс генератором переменного тока;
Частота генератора должна быть равна частоте собственных колебаний контура , при этом характеристические сопротивления равны;
Сопротивление должно быть меньше, чем 2ρ, так как только в этом случае в цепи возникнут свободные колебания, поддерживаемые внешним источником.

Полное сопротивление цепи: 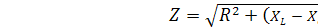=R, так как равны характеристические сопротивления. Следовательно, при резонансе цепь носит чисто активный характер, значит, входное напряжение, и ток в момент резонанса совпадают по фазе. Ток принимает максимальное значение. При максимальном значении тока напряжение на участках L и C будут большими и равными между собой. Напряжение на зажимах цепи: 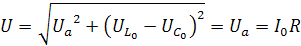. Рассмотрим следующие соотношения: 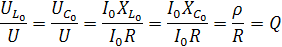, следовательно 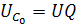. Q–добротность контура –при резонансе напряжения показывает, во сколько раз напряжение на реактивных элементах больше входного напряжения генератора, питающего цепь. При резонансе коэффициент передачи последовательного колебательного контура 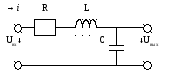резонанса. 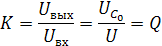Пример: Если добротность равна 100, напряжение на зажимах 1В, то Uc=Ul=QU=100В, то есть напряжение на зажимах меньше напряжений на емкости и индуктивности. Это явление называется резонансом напряжений При резонансе, коэффициент передачи равен добротности. Построим векторную диаграмму напряжения Напряжение на емкости равно напряжению на индуктивности, следовательно напряжение на сопротивлении равно напряжению на зажимах и совпадает по фазе с током. Рассмотрим энергетический процесс в колебательном контуре: В цепи имеется обмен энергии между электрическим полем конденсатора и магнитным полем катушки. К генератору энергия катушки не возвращается. От генератора в цепь поступает такое количество энергии, которое тратится на резисторе. Это необходимо для того, чтобы в контуре наблюдались незатухающие колебания. Мощность в цепи только активная. 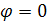Докажем это математически: 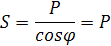, полная мощность цепи, которая равна активной мощности. 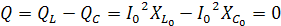, реактивная мощность. 8.1 Резонансная частота. Расстройка. В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер: 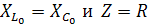Lώ=l/ώC, следовательно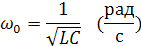 , угловая резонансная частота. Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура. При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуреприсутствует расстройка. Настроить колебательный контур в резонанс можно тремя способами: 1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура 2 Изменять индуктивность катушки, при частоте питания и емкости const; 3 Изменять емкость конденсатора , при частоте питания и индуктивности const. Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора. При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка. Расстройка – отклонение частоты от резонансной частоты. Существует три вида расстройки:

Абсолютная – разность между данной частотой и резонансной

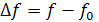
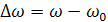
Обобщенная – отношение реактивного сопротивления к активному:

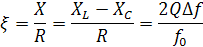
Относительная – отношение абсолютной расстройки к резонансной частоте:

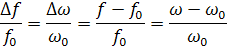При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной, Если больше – положительной. Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты. 8.2 Построение зависимостейX,XL,XC отf.Задачи:

Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.

Решение:

Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.

Решение: Тестовые задания:

Отношение реактивного сопротивления к активному это :

А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка.

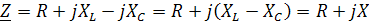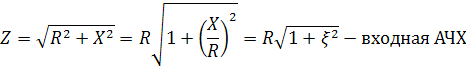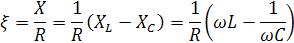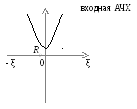
Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура. 9.1 Входные АЧХ и ФЧХ. В последовательном колебательном контуре: , где R – активное сопротивление; X – реактивное сопротивление. Учитывая, что ,то ώ=0 ζ=-∞ Z=∞ ώ=ώ۪۪ζ=0 Z=R ώ=∞ ζ=∞ Z=∞, следовательно график имеет вид: Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается. ζ=0 φ=0 R ζ=1 φ=45° RL ζ=-1 φ=-45° RC ζ=∞ φ=90° L ζ=-∞ φ=-90° C. Построим график: На участке ζ=[-1;1] ФЧХ имеет линейный характер.

На участке ζ=[-∞;0] — цепь носит активно-емкостной характер;
На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;
При ζ=0 — цепь носит активный характер;

Передаточные АЧХ и ФЧХ

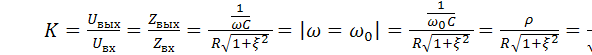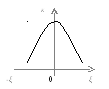передаточная характеристика АЧХ ζ=-∞ k=0 ζ=0 k=Q ζ=∞ k=0 Построим график зависимости: Разделим k∕kои получим передаточную характеристику АЧХ в относительных единицах, которая имеет вид: Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°. На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.

Что такое колебательный контур?

Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.

Также можно сказать, что колебательный контур — это электрическая цепь, работа которой порождает электромагнитное поле.

Но зачем кому-то создавать такие колебания?

Колебательные контуры — неотъемлемая часть многих производственных процессов. С их помощью изготавливают радиоприёмники, генераторы сигналов, блоки измерения частоты, контроллеры частоты напряжения на двигателях.

Возможно, вам может показаться, что это устройство давно устарело и используется в каких-то непонятных вещах, но стоит понимать, что без них не было бы возможно создание домофона, электромагнитов, различных датчиков, с которыми мы встречаемся ежедневно.

Колебательный контур состоит из двух компонентов: катушки и конденсатора, и выглядит вот так:

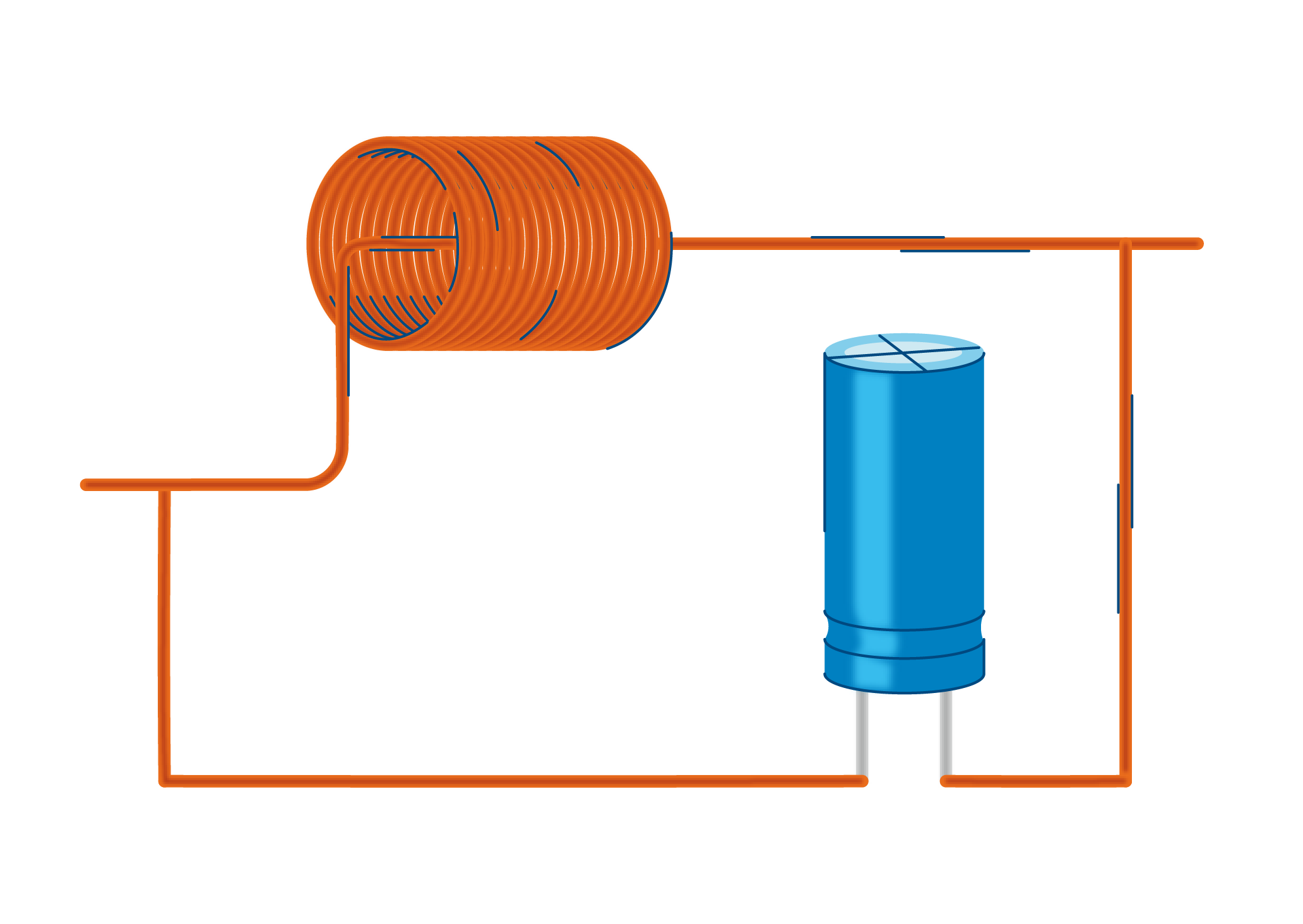
Катушка индуктивности (или соленоид) — это стержень с несколькими слоями обмотки медной проволокой. Именно он создаёт колебания в колебательном контуре. Стержень, находящийся в середине катушки, называется дроссель, или сердечник.

Катушка способна создавать колебания, только если есть электрический заряд. Она обладает низким сопротивлением.

Конденсатор — это элемент, способный накопить в себе большое количество электрического заряда. Он состоит из двух обкладок, между которыми находится диэлектрик (вещество, не проводящее электрический ток).

В чём его отличие от обычного аккумулятора? В аккумуляторе происходит превращение механической, химической, световой и других энергий в электрическую, в конденсаторе же накапливается заряд, который он может отдать весь сразу.

Часто в электрическую цепь колебательного контура подключают ещё один элемент — резистор, который обладает сопротивлением и контролирует силу тока и напряжение в цепи.

Виды колебательных контуров

По типу соединения колебательные контуры можно разделить на последовательный и параллельный.

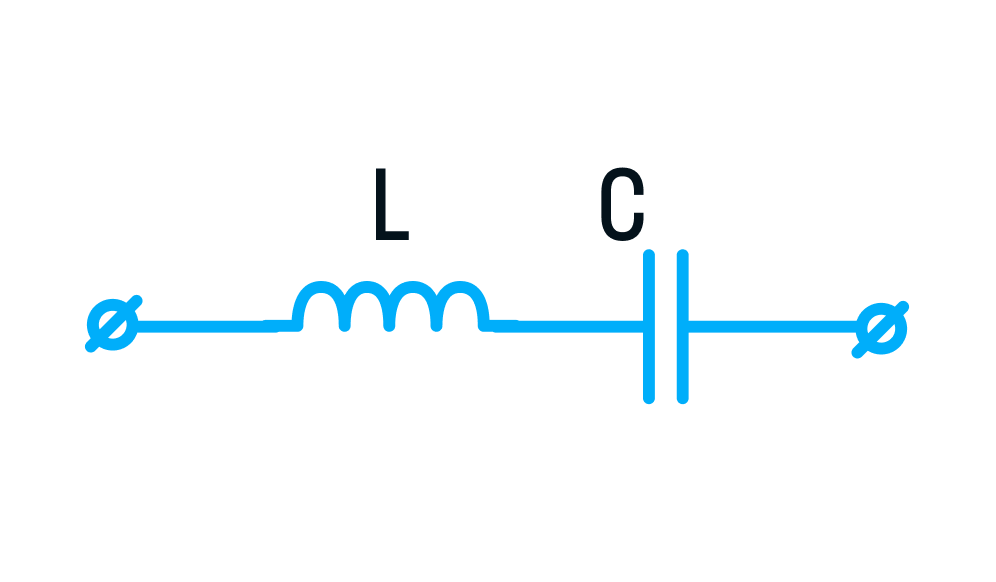
Колебательный контур, схема последовательного соединения

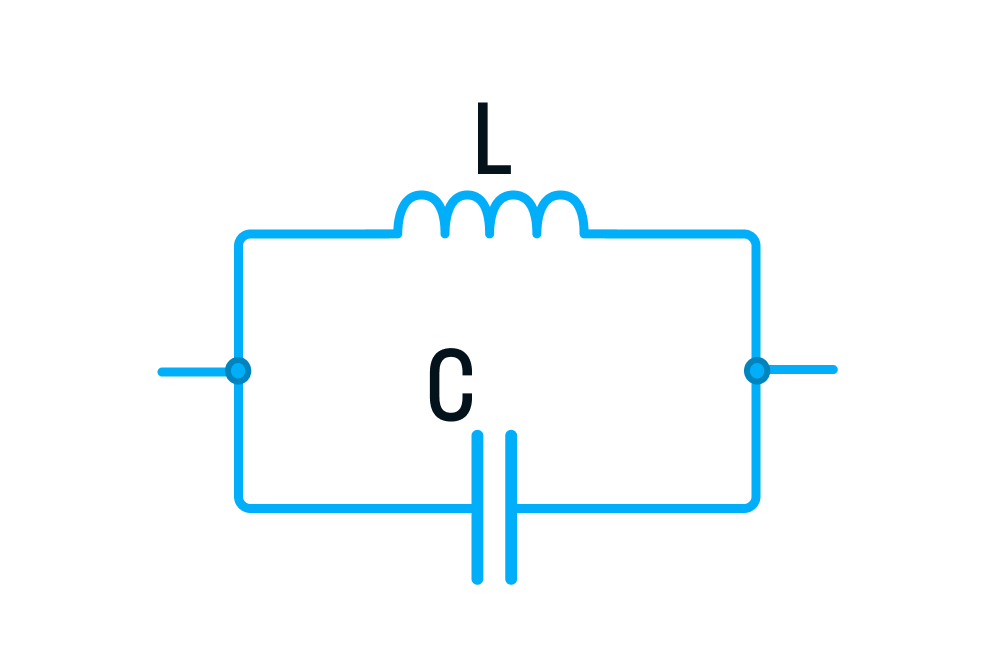
Колебательный контур, схема параллельного соединения

Также физики выделяют особый тип контура — идеальный.

Идеальный колебательный контур — контур, сопротивление которого отсутствует, порождая при этом незатухающие свободные электромагнитные колебания.

Как вы думаете, можно ли создать такой контур и работать с ним на практике? К сожалению, такое маловероятно. Идеальный колебательный контур — всего лишь математическая модель, допущение, с помощью которого можно вывести формулы, ускорить расчёты и оценить характеристики контура в производстве.

Емкостное сопротивление колебательного контура может быть определено выражением

Опубликовано 12.06.2017 по предмету Физика от Гость >> Оцени ответ

Алгебра
Математика
Русский язык
Українська мова
Информатика
Геометрия
Химия
Физика
Экономика
Право
Английский язык
География
Биология
Другие предметы
Обществознание
История
Литература
Українська література
Беларуская мова
Қазақ тiлi

Емкостное сопротивление

Емкостное сопротивление колебательного контура может быть определено выражением?

В 3:31 поступил вопрос в раздел Физика, который вызвал затруднения у обучающегося.

Емкостное сопротивление колебательного контура может быть определено выражением?

Ответ подготовленный экспертами Учись.Ru

Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике «Физика». Ваш вопрос звучал следующим образом:

Емкостное сопротивление колебательного контура может быть определено выражением?

После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:

НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.

Соколова Кармелитта Лаврентьевна — автор студенческих работ, заработанная сумма за прошлый месяц 52 123 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию

ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!

Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:

Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.

Ответы на вопросы — в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.

Полезные статьи — раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.

Красивые высказывания — цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.

Абадзехская стоянка, Даховская пещера. ..
По закону сохранения заряда каждый шарик после соприкас#10..

Наибольшая длина химической связи в молекуле 1) PH3 2) H2O 3) H2S 4) NH3Докажите
Точка К,удаленная от плоскости треугольника АВС ** 4см находится ** равном расстоянии от.
Озаглавте текст срочно пжМы продвигаемся медленно поперек лесной речонки. Мне немного.
Напишите программу, которая выводит первое слово переданной её символьной строки. Слово –.

Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.

2020 — 2023 — UCHEES.RU