Чему равен период и угловая скорость если частота вращения 10 гц

Содержание

11. Маховик вращается с постоянной угловой скоростью 9 рад/с. Определите: а) частоту его вращения; б) период его вращения.

10. Определите угловую скорость вала, вращающегося: а) с периодом 10 с; б) с частотой 30 Гц.

Определить частоту вращения Земли вокруг Солнца

Знаете ответ?
Сомневаетесь в ответе?

Найдите правильный ответ на вопрос ✅ «10. Определите угловую скорость вала, вращающегося: а) с периодом 10 с; б) с частотой 30 Гц. 11. Маховик вращается с постоянной угловой . » по предмету Физика, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.

Похожие вопросы по физике

Помогите! Почему Луна смотрит на Землю только олной стороной? А) она не вращается; 6) период се вращещзя вокруг твоей оси равен периоду обращения вокруг Земли: В) период вращения Земли вокруг своей оси равен периоду обращения Луны;

Маховик, момент инерции которого равен J = 63,6 кг•м2, вращается с постоянной угловой скоростью ω = 31,4 рад/с. Найти тормозящий момент M, под действием которого маховик останавливается через t = 20 с.

Коленчатый вал радиусом R=10 см делает 29 оборотов за 5 с. Определить частоту вращения вала. Определить угловую и линейную скорость точек поверхности вала.

Маховик, момент инерции которого равен 63,6 кг м^2, вращ. с постоянной угловой скоростью 3,14 рад/с. Найти тормозящий момент, считая его постоянным, под дей-м которого маховик останавливается через 20 с (помогите с решением, ответ должен быть таким:

При увеличении линейной частоты вращения в 2 раза А) период вращения возрастает в 2 раза; В) период вращения возрастает в 2π раза; С) период вращения уменьшается в 2π раза; D) период вращения уменьшается в 2 раза; Е) период вращения не изменяется

Помогите с ответом
решить уравнение 2 целых 2.9:y=3 целых 19.27:3 целых 1.3
Нет ответа

дачнику до железной платформы нужно пройти 2 км. с какой средней скоростью нужно идти. чтобы успеть на электр-ку которая прибудет на платформу через полчаса? запиши ответ с помощью знака > или равно, обозначив средн. скорость буквой U

10. Определите угловую скорость вала, вращающегося: а) с периодом 10 с; б) с частотой 30 Гц.

Определить частоту вращения Земли вокруг Солнца

Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.

Знаете ответ на вопрос?
Не уверены в ответе?

Правильный ответ на вопрос «10. Определите угловую скорость вала, вращающегося: а) с периодом 10 с; б) с частотой 30 Гц. 11. Маховик вращается с постоянной угловой . » по предмету Физика. Развернутая система поиска нашего сайта обязательно приведёт вас к нужной информации. Как вариант — оцените ответы на похожие вопросы. Но если вдруг и это не помогло — задавайте свой вопрос знающим оппонентам, которые быстро дадут на него ответ!

Похожие вопросы по физике

Помогите с ответом
Найдите площадь ромба, если его высота равна 16 см, а острый угол равен 30
Нет ответа

Сделайте синтасический разбор предложений: Быстро растаял под лучами яркого солнца снег. Хороши летом глазастые ромашки! Идёшь в тишине, и уха коснётся трубный звук.

Нет ответа
С. Сахарнов «Летучая рыба»
Нет ответа
Вычислите: 4/5 * 10/27 * 15/16 4/7 * 35/36 * 3/5 30/77 * 11/18 * 3/25 20/13 * 39/100 * 10/21
Нет ответа

Объясните, почему уважение американцев к труду можно считать одной из причин подъёма экономики. 19 Век

Нет ответа

Главная » Физика » 10. Определите угловую скорость вала, вращающегося: а) с периодом 10 с; б) с частотой 30 Гц. 11. Маховик вращается с постоянной угловой скоростью 9 рад/с. Определите: а) частоту его вращения; б) период его вращения. 10.

Центростремительное (нормальное) ускорение

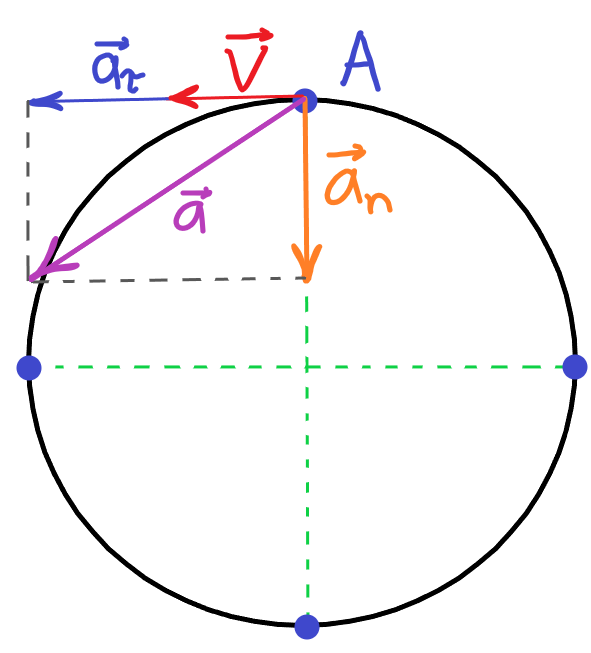
Рис.3. Центростремительное ускорение

Вернемся к нашему примеру с мотоциклистом, двигающимся по мототреку в форму окружности. (См. Рис.3.) Для начала, представим, что линейная скорость у мотоциклиста постоянна, то есть он двигается равномерно, а значит его ускорение должно быть равно нулю. Это действительно так, но при движении по окружности (или любой другой криволинейной траектории) даже с постоянной скоростью возникает новый вид ускорения – центростремительное, еще его называют «нормальное», ускорение. Оно появляется по причине изменения направления вектором скорости.

На самом деле, для решения задач понимать природу центростремительного ускорения совсем необязательно. Достаточно просто помнить, что при любом криволинейном движении появляется такое ускорение. Его можно вычислить по формуле: $a_n=frac;$ где (V) –линейная скорость;

(R) – радиус окружности.

Подставим сюда линейную скорость через угловую — (V=omega*R). И получим еще одну формулу для центростремительного ускорения: $a_n=omega^2*R;$ Важно! Центростремительное ускорение всегда перпендикулярно скорости и направлено к центру окружности.

Тангенциальное ускорение

Теперь представим, что мотоциклист едет по круглому мототреку не с постоянной скоростью, а равноускорено/равнозамедлено. В этом случае говорят, говорят, что мотоциклист движется с тангенциальным ускорением.

Тангенциальное ускорение – это обычное ускорение, к которому мы привыкли в курсе кинематики. Оно показывает на сколько успевает измениться скорость за единицу времени, например, за секунду.

Тангенциальное ускорение всегда направлено по касательной к траектории. Если тело ускоряется, то оно сонаправлено с линейной скоростью, а если замедляется, то направлено в противоположную сторону. (см.Рис.3, показано синей стрелкой (vec>))

При равноускоренномравнозамедленном движении тангенциальное ускорение можно посчитать по формуле: $a_=frac;$ где (V_к) – конечная скорость;

(V_н) – начальная скорость;

(t) – время, за которое скорость изменилась с (V_н) до (V_к).

При любом неравномерном движение по криволинейной траектории (окружности), у тела обязательно есть два вида ускорений – нормальное, направленное к центру, перпендикулярно скорости, и тангенциальное, направленное по касательной к траектории. Нормальное ускорение отвечает за изменение направления вектора линейной скорости, а тангенциальное за изменение величины линейной скорости.

Если тело движется с постоянной скоростью, то тангенциальное ускорение равно (0).

Если тело движется по прямой, то нормальное ускорение равно (0).

Векторно сложим эти два ускорения по правилу параллелограмма, и получим вектор общего ускорения, которым обладает тело при движении по окружности. (см. Рис.3., фиолетовая стрелка (vec)).

Колесо радиуса R вращается с постоянной скоростью. Во сколько раз отличаются центростремительные ускорения двух точек расположенный на расстояниях (R/2) и (R/3) от центра колеса

Решение: Так как любая точка колеса вращается с одинаковой угловой скоростью (omega), то воспользуемся формулой для центростремительного ускорения через угловую скорость: $a_n=omega^2*r;$ Пусть точка А вращается по окружности радиусом (R/2), а точка В — (R/3). $a_=omega^2*frac;$ $a_=omega^2*frac;$ $frac=frac<omega^2*frac><omega^2*frac>=frac*frac=1,5$ Ответ:(frac=1.5.)

Центростремительное ускорение

Определение и формула

Центростремительное ускорение — ускорение с постоянным модулем, но меняющимся направлением. Поэтому оно вызывает изменение направления вектора скорости, но не изменяет его модуль. Центростремительное ускорение обозначается как aц.с.. Единица измерения — метры на секунду в квадрате (м/с 2 ). Центростремительное ускорение можно выразить через линейную и угловую скорости, период, частоту и количество оборотов/время:

Пример №3. Рассчитать центростремительное ускорение льва, спящего на экваторе, в системе отсчета, две оси которой лежат в плоскости экватора и направлены на неподвижные звезды, а начало координат совпадает с центром Земли.

Спящий лев сделает один полный оборот тогда, когда Земля сделает один оборот вокруг своей оси. Земля делает это за время, равное 1 сутки. Поэтому период обращения равен 1 суткам. Количество секунд в сутках: 1 сутки = 24•60•60 секунд = 86400 секунд = 86,4∙10 3 секунд.

Радиус Земли равен 6400 км. В метрах это будет 6,4∙10 6 . Теперь у нас есть все, что нужно для вычисления центростремительного ускорения. Подставляем данные в формулу:

Текст: Алиса Никитина, 29.4k

Задание EF18273

Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Центростремительное ускорение автомобиля равно.

Алгоритм решения

Записать исходные данные.
Записать формулу для определения искомой величины.
Подставить известные данные в формулу и произвести вычисления.

Решение

Записываем исходные данные:

Радиус окружности, по которой движется автомобиль: R = 100 м.
Скорость автомобиля во время движения по окружности: v = 20 м/с.

Формула, определяющая зависимость центростремительного ускорения от скорости движения тела:

Подставляем известные данные в формулу и вычисляем:

Задание EF17763

Точка движется по окружности радиусом R с частотой обращения ν. Как нужно изменить частоту обращения, чтобы при увеличении радиуса окружности в 4 раза центростремительное ускорение точки осталось прежним?

а) увеличить в 2 раза б) уменьшить в 2 раза в) увеличить в 4 раза г) уменьшить в 4 раза

Алгоритм решения

Записать исходные данные.
Определить, что нужно найти.
Записать формулу зависимости центростремительного ускорения от частоты.
Преобразовать формулу зависимости центростремительного ускорения от частоты для каждого из случаев.
Приравнять правые части формул и найти искомую величину.

Решение

Запишем исходные данные:

Центростремительное ускорение определяется формулой:

Запишем формулы центростремительного ускорения для 1 и 2 случаев соответственно:

Так как центростремительное ускорение в 1 и 2 случае одинаково, приравняем правые части уравнений:

Произведем сокращения и получим:

Это значит, чтобы центростремительное ускорение осталось неизменным после увеличения радиуса окружности в 4 раза, частота должна уменьшиться вдвое. Верный ответ: «б».

Угловая скорость.

Угловой скоростью называется величина, численно равная скорости точек, расположенных от оси на расстоянии единицы длины.

При вращении тела вокруг неподвижной оси АВ каждая точка тела М описывает окружность, перпендикулярную к оси, центр Р которой лежит на оси.

Скорость точки M направлена нормально к плоскости МАВ в сторону вращения. Равномерное вращение точки характеризуется постоянной угловой скоростью.

Угловой скоростью тела называют отношение угла поворота к интервалу времени, в течение которого совершен этот поворот. Если угловую скорость обозначить через w, то:

Угловая скорость выражается в радианах в секунду (рад/с).

При равномерном вращении, когда известна угловая скорость в начальный момент времени t0 = 0, можно определить угол поворота тела за время t и тем самым положение точек тела:

За один период (промежуток времени Т, в течение которого тело совершает один оборот по окружности) угол поворота φ равен 2π рад: 2π = wT, откуда:

Связь угловой скорости с периодом Т и частотой вращения ν выражается соотношением:

А связь между линейной и угловой скоростями определяется соотношением:

Период и частота вращения

Важными характеристиками любого вращательного движения являются частота и период:

Определение Период – время, за которое тело совершает полный оборот.

В нашем примере с мотоциклистом, период – это время, за которое мотоциклист проезжает один полный круг.

Из курса геометрии вспоминаем, что длину дуги окружности можно посчитать как (2*pi*R), где (R) – радиус окружности. Тогда в случае равномерного движения период можно посчитать по формуле, как расстояние деленое на скорость: $T=frac<2*pi*R>;$ Подставив сюда формулу ((1)) для линейной скорости через угловую: $T=frac<2*pi><omega>;$ Где (V) –линейная скорость вращения.

В системе СИ период измеряется в ([^]).

Определение Частота – количество оборотов за единицу времени.

В случае с мотоциклистом, частота – это сколько кругов он успевает проехать, например, за один час. Обычно частоту измеряют в оборотах в секунду.

Период и частота вращения связаны между собой выражением: $T=frac;$ Отсюда можно получить формулы для частоты, подставив период: $nu=frac<2*pi*R>=frac<omega><2*pi>;$

Скорость точки, находящейся на краю вращающегося диска равна (V_A=15(м/с)), а точки, расположенной на 0,2 (м) ближе к центру вращения равна (V_B=10(м/с)). Найти частоту вращения и радиус диска.

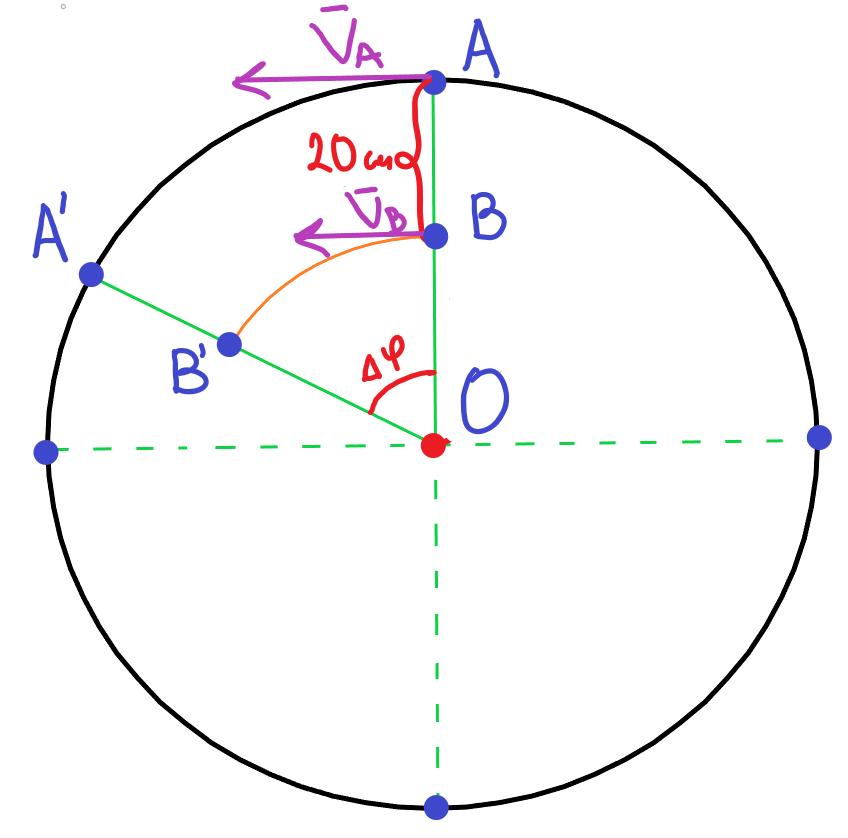
Рис.2. Задача на движение по окружности

Решение: Точка (А) находится дальше от центра на (20 (см)), а значит ее скорость больше, чем у точки (В). По условию так и есть. Так как обе точки находятся на одном радиусе, то угловые скорости у них одинаковые. Распишем угловые скорости для точек (А) и (В) и приравняем: $omega_A=frac;$ $omega_B=frac;$ $omega_A=omega_B;$ $frac=frac;$ Из условия (A0=BO+0.2): $frac=frac;$ $frac=frac;$ $15*BO=(BO+0,2)*10;$ $5*BO=2;$ $BO=0,4.$ Мы нашли радиус окружности по которой вращается точка (В), тогда радиус точки (А) будет на (0,2(м)) больше — (0,6(м)).

Для того, чтобы найти частоту, воспользуемся формулой: $nu=frac<2*pi*R_A>=frac=3,98(об/сек);$ Ответ: (R=0,6(м)) и (nu=3,98(об/сек).)