Лекции и задачи по ТОЭ. На сайте представлен лекционный материал для изучения теоретических основ электротехники и видеоуроки по всем темам. Так же тут можно заказать решение задач, курсовых, расчетных, контрольных и домашних работ. Онлайн помощь на экзамене, контрольной. Решение тестов, занятия по скайпу и др. В ближайшее время на сайт будут добавлены готовые работы на разные темы ТОЭ, ТАУ и другим дисциплинам.
Теория / 7.1. Понятие частотной характеристики
Пусть внешнее воздействие задано в виде тока или напряжения источника, а искомая реакция (отклик) представляет собой ток или напряжение нагрузки (рис. 7.1).
Размерность комплексной частотной характеристики (КЧХ) определяется отношением размерностей отклика и воздействия. Если отклик является напряжением, а воздействие – током, то КЧХ имеет размерность сопротивления; если отклик – ток, а воздействие – напряжение, то КЧХ – проводимость; если и отклик и воздействие являются током или напряжением, то КЧХ безразмерная величина.
Комплексную частотную характеристику, как и любое комплексное число, можно записать в показательной и алгебраической форме:
модуль комплексной частотной характеристики, равный отношению амплитуд или действующих значений отклика цепи и внешнего воздействия.
аргумент, представляющий собой разность фаз отклика и воздействия.
Зависимость модуля КЧХ H(w) от частоты называется амплитудно-частотной характеристикой (АЧХ). Зависимость аргумента от частоты называется фазо-частотной характеристикой (ФЧХ).
Графически строят отдельно АЧХ и ФЧХ либо изображают зависимость от частоты действительной и мнимой частей КЧХ.
Комплексную частотную характеристику можно изобразить в виде одной зависимости – годографа КЧХ на комплексной плоскости (рис. 7.2).
Годограф – это геометрическое место концов вектора H(jw), соответствующих изменению частоты от На годографе указывают точки, соответствующие некоторым значениям частоты, и стрелкой указывают перемещение конца вектора H(jw) при увеличении частоты.
Годограф дает представление как об АЧХ и ФЧХ, так и о частотной зависимости действительной и мнимой составляющих, поэтому его иногда называют амплитудно-фазовой частотной характеристикой (АФЧХ).
Комплексная частотная характеристика называется входной (ВЧХ), если отклик у ( t ) и внешнее воздействие х( t ) рассматриваются на одних и тех же зажимах цепи (рис. 7.3, а). Например, если х( t ) = i ( t ) – ток на входе цепи, а у( t ) = u ( t ) – напряжение на входе цепи, то ВЧХ – комплексное входное сопротивление по отношению к зажимам «а b »
Комплексная частотная характеристика называется передаточной (переходной), если отклик у ( t ) и внешнее воздействие х ( t ) рассматриваются на разных зажимах цепи (рис. 7.3, б). Например, отклик у ( t ) = ucd ( t ) – напряжение на выходе цепи, а внешнее воздействие х( t ) = uab ( t ) – напряжение на входе цепи.
Что такое АЧХ(Амплитудно Частотная Характеристика)
В этом случае КЧХ представляет собой комплексный коэффициент передачи по напряжению
Коэффициент передачи – величина безразмерная.
Физический смысл АЧХ и ФЧХ
АЧХ показывает, как зависит коэффициент передачи системы от частоты входного гармонического сигнала. Иными словами, АЧХ демонстрирует, во сколько раз изменится амплитуда синусоидального сигнала после прохождения через систему, в зависимости от его частоты. ФЧХ же характеризует зависимость сдвига фазы выходного сигнала относительно входного.
Наглядно это можно продемонстрировать на примере простейшего RC-фильтра:
| Входная частота, Гц | 1 | 10 | 100 |
| АЧХ (кратность ослабления) | 0,1 | 0,9 | 1 |
| ФЧХ (сдвиг фазы) | -80° | -10° | 0° |
Видно, что на низких частотах происходит заметное ослабление амплитуды и сдвиг фазы, а при повышении частоты АЧХ стремится к единице (ослабление становится минимальным), а ФЧХ — к нулю.
Способы построения АЧХ и ФЧХ
Существует несколько подходов к построению частотных характеристик:
- Аналитический метод
- Экспериментальный метод
- Графоаналитический метод
Рассмотрим их подробнее.

Пример 1
В качестве примера построим АФЧХ для демпфера, модель которого разобрана в этой статье. . Добавим на схему блок «Построение частотных характеристик», в качестве входа возьмем возмущающее воздействие, в качестве выхода — положение положение груза. Для наглядности иллюстрации примем в качестве выхода положение в миллиметрах (х1000), поскольку модель у нас размерная и результат получается в метрах уже достаточно маленьким примерно 0.004 метра. см. рис. 3.11

Рисунок 3.1.11 Схема для построения частотных характеристик.
Параметры блока «Построение частотных характеристик» приведены на рисунке 3.1.12, для иллюстрации зависимости АЧХ и ЛАХ. Результат работы блока — график с выбранными параметрами — изображен на рисунке 3.1.13:

Рисунок 3.1.12 – Параметры блока «Частотные характеристики».
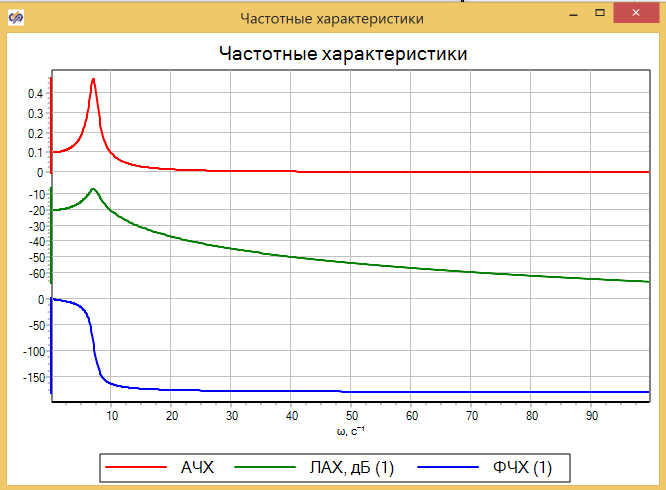
Рисунок 3.1.13 – Частотные характеристики в АЧХ, ЛАХ, ФЧХ в линейном масштабе по ω.
Анализ графика в линейном масштабе по ω чаще всего не очень удобен, поскольку весь график собирается в узкой области, а дальше график абсолютной амплитуды практически сливается с 0. Если мы хотим исследовать частоты хотя бы до 1000 Гц, мы увидим практически вертикальные и горизонтальные прямые. Изменения масштаба шкалы АЧХ и ω на логарифмический дает возможность лучше исследовать частотные характеристики (см. рис. 3.1.14).
На рисунке 3.1.14 представлены частотные характеристики демпфера в логарифмическом масштабе и иллюстрация соотношения между абсолютной величиной амплитуды АФЧХ и ЛАХ в децибелах.
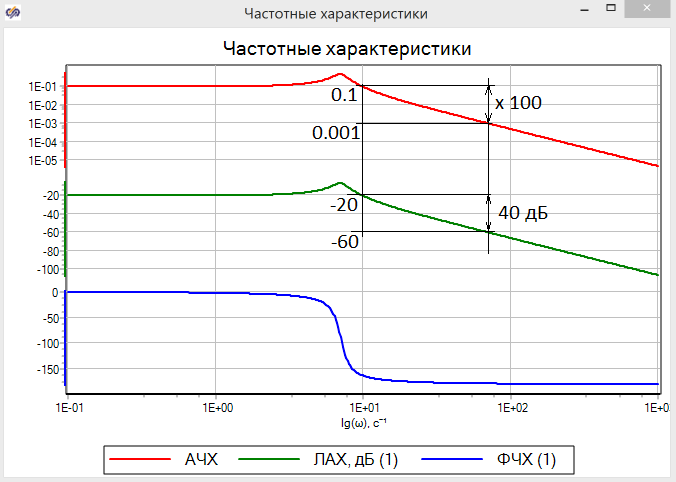
Рисунок 3.1.14 – Частотные характеристики в АЧХ, ЛАХ, ФЧХ в логарифмическом масштабе по ω.
Пример 2
Постоим частотные характеристики для чуть более сложной модели, а именно — для гидравлического демпфера, рассмотренного в предыдущей лекции.
Для начала посмотрим на модель в виде блоков.
Модель, подготовленная для анализа, представлена на рисунке 3.1.15. В отличие от исходной модели, описанной ранее, входное воздействие задается блоком «ступенька» с скачком с 0 до 1 на 10 секунде расчёта. В блоке «линейная функция» происходит пересчет сигнала «ступенька»:
0 — соответствует 200 бар в камере (конечное состояние в предыдущем примере)
1 — соответствует 400 бар в камере.
Это сделано для того, чтобы можно было подавать синусоидальный сигнал и не получать отрицательное давление в камере плунжера. Также для наглядности графика мы усиливаем выходное перемещение, переводя его из метров в миллиметры.
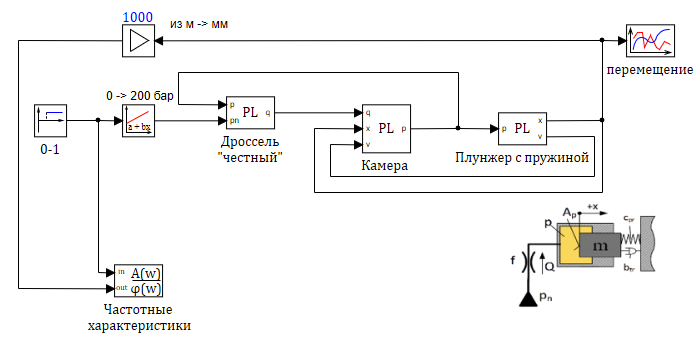
Рисунок 3.1.15 – Модель гидравлического демпфера.
Частотные характеристики, получаемые в конце расчёта, приведены на рисунке 3.1.16. Видно что характеристики отличаются от простого пружинного демпфера (сравните с 3.1.14)
Рисунок 3.1.16 – Частотные характеристики гидравлического демпфера
Блок «Построение частотных характеристик» осуществляет расчет характеристик для линеаризованной модели в окрестности заданной точки. Это означает, что частотные характеристики системы в разные моменты времени могут отличаться для нелинейных моделей. Например, в нашем случае характеристики в начале расчёта будут отличаться от характеристик, полученных в конце расчёта.
Для подробных и нелинейных моделей, блок «Построение частотных характеристик» может не работать из за наличия разрывов и нелинейностей в модели. Как например, для «точной» модели демпфера, которую мы проверяли в предыдущей статье. В этом случае возможно построить частотные характеристики непосредственно моделированием, путем подачи синусоидального сигнала с разной частотой и измерения отклика. В SimInTech для этого используется блок «Гармонический анализатор», который подключается ко входу модели и генерирует синусоидальное воздействие. В этот же блок направляется отклик системы, и производится вычисление необходимых параметров для построения различных характеристик системы, которые можно вывести на графики с помощью блока «фазовый портрет».
Модель гидравлического демпфера, собранного из библиотечных блоков SimInTech, представлена на рисунке 3.1.7

Рисунок 3.1.17 – Модель гидравлического демпфера для расчёта частотных характеристик.
Расчеты с моделью показывают, что при сохранении общего вида графиков значения, полученные для «подробной модели», отличаются от линеаризованной модели (см. рис. 3.18 — 3.19)
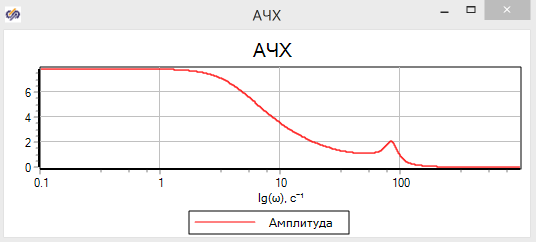
Рисунок 3.1.18 – АЧХ подробной модели привода, полученная прямым моделированием.

Рисунок 3.1.19 – ЛАХ подробной модели привода, полученная прямым моделированием.
Использование прямого моделирования для получения характеристик является более надежным способом и работает не только с линейными моделями, но также может быть применимо для построения характеристик некоторых реальных объектов, если их можно подключить к среде моделирования и воздействовать в реальном режиме времени. Однако затраты на вычисления значительно будут больше. Например, для получения характеристик демпфера пришлось выполнить процесс в 40 000 секунд модельного времени, на обычном компьютере это заняло порядка 35 минут. График процесса перемещения плунжера в процессе вычисления характеристик приведен на рисунке 3.1.20.

Рисунок 3.1.20 – Перемещения плунжера в процессе моделирования.
Блок «Гармонический анализатор» имеет выходы:
Re(w*t) – текущее значение действительной части амплитудно-фазовой частотной характеристики исследуемой системы;
Im(w*t) – текущее значение мнимой части амплитудно-фазовой частотной характеристики.
Это позволяет построить годограф исследуемой системы с помощью фазового портрета. (см. рис. 3.1.21)

Рисунок 3.1.21 – Годограф системы гидравлического демпфера.
Модели, использованные для иллюстрации в лекции можно взять здесь
Виды частотных характеристик
Частотные характеристики системы могут быть представлены в двух видах: амплитудно-частотной характеристике (АЧХ) и фазо-частотной характеристике (ФЧХ).
Амплитудно-частотная характеристика (АЧХ)
АЧХ показывает, как амплитуда выходного сигнала системы зависит от частоты входного сигнала. Она представляет собой график, на котором по оси X откладывается частота, а по оси Y откладывается амплитуда выходного сигнала.
АЧХ может иметь различные формы, такие как плоская, полосовая, полосовая с резонансом и т. д. Форма АЧХ позволяет определить, как система реагирует на различные частоты входного сигнала.
Фазо-частотная характеристика (ФЧХ)
ФЧХ показывает, как фаза выходного сигнала системы зависит от частоты входного сигнала. Она также представляет собой график, на котором по оси X откладывается частота, а по оси Y откладывается фаза выходного сигнала.
ФЧХ может иметь различные формы, такие как линейная, нелинейная, скачкообразная и т. д. Форма ФЧХ позволяет определить, как система изменяет фазу сигнала при различных частотах.
АЧХ и ФЧХ являются взаимосвязанными характеристиками и вместе описывают поведение системы в частотной области. Они позволяют анализировать и синтезировать системы автоматического управления, оптимизировать их работу и достичь требуемых характеристик.
Амплитудно-частотная характеристика (АЧХ)
Амплитудно-частотная характеристика (АЧХ) – это график, который показывает зависимость амплитуды выходного сигнала системы от частоты входного сигнала при постоянной фазе.
На графике АЧХ по оси X откладывается частота входного сигнала, а по оси Y – амплитуда выходного сигнала.
АЧХ позволяет определить, как система изменяет амплитуду сигнала при различных частотах. Она показывает, как система пропускает или подавляет различные частоты входного сигнала.
АЧХ может иметь различные формы, такие как плоская, полосовая, полосовая с резонансом и т. д. Форма АЧХ позволяет определить, как система изменяет амплитуду сигнала в зависимости от его частоты.
АЧХ является одной из основных характеристик системы автоматического управления. Она позволяет анализировать и синтезировать системы, оптимизировать их работу и достичь требуемых характеристик.
Комплексный коэффициент передачи. АЧХ и ФЧХ цепи




Комплексный коэффициент передачи – это отношение комплексного сигнала на выходе к комплексному сигналу на входе при установившемся режиме работы устройства или системы (сигнал на входе действует бесконечно долго).
Формула для определения комплексного коэффициента передачи выглядит следующим образом:
где, Y(jw) — комплексная амплитуда выходного сигнала; X(jw) — комплексная амплитуда входного сигнала.
Понятие комплексного коэффициента передачи, как правило, используется в акустике, оптике, электротехнике, электронике. Например, коэффициент усиления усилителей, ослабление электромагнитного излучения в поглощающих средах, коэффициент затухания сигнала в линиях электропередачи, усиление света в активных средах лазера.
Получи помощь с рефератом от ИИ-шки
ИИ ответит за 2 минуты
Существуют следующие методы измерения коэффициента передачи:
- Использование измерителя комплексных коэффициентов передачи и импеданса (комплексное сопротивление между двумя узлами электрической цепи).
- Прямое измерение, заключающееся в измерении амплитуды сигнала на выходе и входе системы и последующее вычисление. Для этого применяются специальные электрические и оптические приборы.
- Измерение методом сравнения, которое осуществляется при помощи аттенюатора (прибор для фиксированного понижения интенсивности электрических и электромагнитных колебаний).
Амплитудно-частотная характеристика и фазо-частотная характеристика цепи
Определение 2
Амплитудно-частотная характеристика – это зависимость амплитуды колебаний (установившихся) выходного сигнала системы от частоты входного гармонического сигнала.
Понятие амплитудно-частотной широко используется в средствах связи, радиолокации и других радиотехнических приложениях. Данный показатель характеризует степень защищенности системы от помех. В многоканальных системах, таких как цифровые антенны, важная роль принадлежит межканальная идентичность амплитудно-частотной характеристики с коэффициентом корреляции, значение которого может достигать 0,999. Чем выше данный показатель (и чем шире полоса частот), тем лучше и проще можно минимизировать мультипликативные помехи, возникающие во время межканальной обработки сигналов.
Начинай год правильно
Выигрывай призы на сумму 400 000 ₽
Традиционный метод измерения амплитудно-частотной характеристики заключается в подаче на вход исследуемого объекта гармонического сигнала с изменяемой частотой и с известной или постоянной амплитудой. В этом случае измерению подвергаются отношение модулей амплитуды выходного и выходного сигналов (коэффициент передачи) для разных значений частоты.
Для того, чтобы сократить время, за которое формируется амплитудно-частотная характеристика, используются специальный генератор, способный перестраивать частоту собственного сигнала с не меняющейся во времени амплитудой (генератор качающейся частоты). Данные генераторы плавно изменяют частоту генерации от низких до высоких, после чего переключают частоту на низшую, данный процесс повторяется периодически. Недостатками данных методов являются:
- Они являются непригодными для устройств с функционирующей регулировкой усиления, задача которой заключается в выравнивании различий в значениях амплитудно-частотных характеристик.
- Они не позволяют произвести оценку интермодуляционных искажений, возникающих между сигналами разных частот.
- Они не позволяют когерентное накопление во времени напряжений сигнала для частотных компонентов.
Существуют измерители амплитудно-частотной характеристики, которые подают на вход рассматриваемой системы широкополосные сигнал или импульс с коротким фронтом, а также измерители с шумовым сигналом, имеющий постоянную спектральную плотность мощности. Отклик анализируется анализатором спектра или фурье-измерителем амплитудно-частотной характеристики, который автоматически выполняет фурье-преобразование.
Фазо-частотная характеристика представляет собой зависимость между частотой сдвига выходного напряжения (сигнала) и входным напряжением при усилении гармонических колебаний.
Если фазо-частотная характеристика не искажает форму усиливаемых колебаний, то она представляет собой линейную зависимость фазового сдвига от частоты:
$j(f) = –t3 • 2 • p • f$
где, j(f) — фазовый сдвиг между входным и выходным напряжением; t3 — время задержки; f — частота, на которой осуществляется измерение фазового сдвига.
Для идеальной фазо-частотной характеристики сдвиг j прямо пропорционален частоте. Угол наклона такой фазо-частотной характеристики определяет время запаздывания сигнала на выходе. Если данный угол равен нулю, то это означает, что выходной сигнал появляется одновременно с входным. По графику фазо-частотной характеристики производится оценка фазовых искажений, вносящихся усилителем. Пример фазо-частотной характеристики изображен на рисунке ниже.
Рисунок 1. Фазо-частотная характеристика. Автор24 — интернет-биржа студенческих работ
Фазовые искажения должны обязательно учитываться в устройствах, которые охвачены глубокой обратной связью, а также в усилителях высококачественного воспроизведения, стереофонических усилителях и т.п.
Амплитудно-частотная и фазо-частотная характеристики представляют собой одни из самых важнейших характеристик систем и приборов, использующихся в радиотехнике, электротехнике и электронике.
Такое знакомое слово «АЧХ»
Кто же прав? Категория топящих за ровную АЧХ, куда нередко заносят всех, кто пользуется измерениями и прочими объективными показателями, или же те, кто считает уши единственным инструментом при выборе?
В такой постановке вопроса – никто. Первая категория внезапно(!) также может считать прослушивание обязательным этапом, а вторую может легко надурить showroom sound некоторых систем, да и в целом, путь отрицания измерений в конечном счёте приведёт к постоянному поиску, хотя, для некоторых это – стиль жизни.
Моя прошлая заметка была встречена довольно позитивно, что навело на мысль о том, что стоит попробовать повторить нечто подобное.
Итак, тема сегодняшнего разговора – АЧХ. Вроде так просто, а когда начинаешь разбираться…
Этот текст, как и прошлый, направлен на объяснение общих основ, без сверхглубокого погружения и перегруза информацией. Для желающих узнать больше есть audiosciencereview.com aka ASR, с их базой обучающих статей и видео, а также книга Floyd Toole “Sound Reproduction: The Acoustics and Psychoacoustics of Loudspeakers and Rooms”, в которой подведён итог почти полувековых исследований систем звуковоспроизведения.
АЧХ или амлитудно-частотная характеристика (она же frequency response aka FR), по сути, показывает зависимость выходного уровня от входного. На вход системы подаётся сигнал определённого, фиксированного, уровня, а с выхода снимается значение выходного напряжения (в нашем случае звуковое давление). Соответственно все девиации выходного напряжения или звукового давления и будут являться неравномерностями ачх.
Казалось бы, всё просто: с механоакустическими преобразователями, как и в случае с электроникой нужно стремиться к наиболее точной передаче дельта-функции Дирака, т.е. иметь приближенный к идеальному импульс. Из этого должно следовать, что устройство должно обладать линейной АЧХ (амплитудно-частотной характеристикой) и ФЧХ (фазо-частотной характеристикой), т.е. «ачх» и «фаза» не должны изменяться в полосе пропускания, что, как можно догадаться, невозможно вследствие самого способа преобразования и влияния внешней среды в виде помещения.
С другой стороны, в отличие от усилителя или ЦАПа, для акустики невозможно вывести/измерить единственную частотную характеристику, которая всегда соотносилась бы с ощущениями при прослушивании. Происходит это по одной простой причине: поведение АС вне оси.
То, что отдаёт акустика при отклонении от некоторой оси излучения отличается по спектральному составу от того, что излучается на оси и используется нашим мозгом для начального определения тембра. Как я уже писал, первичные отражения важны для нас в контексте определения тембрального баланса, а значит система с ровной ачх на оси, но имеющая значительную неравномерность внеосевых ачх не будет являться нейтральной с точки зрения слушателя. То есть то, что обычно выдаётся производителями за ачх, по сути, мало говорит нам о системе, несмотря на то что всё равно является шагом в правильном направлении.
Зная о возможностях DSP в контексте эквализации, можно задаться вопросом: разве нельзя просто проэквализировать? Зачем нам покупать хорошую колонку, если можно исправить дешёвую? Если…
Подавая один сигнал на вход, мы получим разный сигнал на выходе в каждой точке помещения. Этот принцип: на вход один — на выход много и препятствует простой и безболезненной эквализации всего играющего.
«Исправив» на системе с ровной АЧХ на оси, проблемы с внеосевыми АЧХ мы ухудшим прямой звук, на который мозг ориентируется в первую очередь ==> тональный баланс нарушен
«Исправив» на системе с кривой АЧХ на оси, но равномерно спадающими внеосевыми АЧХ эту самую АЧХ на оси, мы одновременно ухудшим тональный баланс внеосевых ачх ==> ухудшим реверберационный фон помещеия ==> тональный баланс нарушен
К чему же мы приходим? Для оценки АС, как некой закрытой системы, нам необходима серия измерений, которая покажет поведение на оси и при отклонении от неё. Это может быть серия графиков или сделанная на их основе диаграмма направленности, что спокойно делается даже в условиях дома, без помощи безэховой камеры.
И вот тогда, тогда уже можно полноценно говорить об оценке тонального баланса системы имея на руках лишь результаты измерений. Найти подобную иформацию можно на spinorama.org , где, как ясно из названия, собрано большое количество spinorama-измерений (измерений по стандарту CTA-2034).
Под конец наглядно покажу разницу между двумя противоположностями: B gf = afdf–bfcf.
Отсюда мощность кросс–спектра равна:
![]()
то есть равна произведению амплитуд спектров двух процессов, является квадратичной оценкой, измеряемой в мкВ 2 . Линейная оценка амплитуды кросс-спектра или кросс-АЧХ, соответственно, равна .
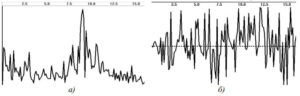
График кросс-АЧХ
График кросс-АЧХ (рис. 5а) наглядно показывает, на каких частотах в обоих процессах присутствуют высокоамплитудные и сравнимые по величине гармоники. Как видно из рис. 5а, основные амплитуды кросс–спектра сосредоточены в районе 8 Гц альфа–диапазона, что типично для затылочных отведений ЭЭГ в состоянии релаксации. Кроме того, пики взаимной активности меньшей амплитуды наблюдаются в диапазонах дельта и тета. Из–за высокого разрешения по частоте график содержит много случайных флюктуаций, поэтому может оказаться полезным его сглаживание. В исследованиях ЭЭГ кросс-АЧХ как оценочный показатель самостоятельного применения не получил.
Преимуществом кросс-АЧХ (перед рассмотренной ниже когерентностью) является то, что ее смысл интуитивно понятен и она вычисляется на одной эпохе анализа, то есть применима для анализа кратковременных процессов.
Кросс-фазовый спектр
Кросс-фазовый спектр φxy(f)=arctg(gf/ef) после подстановки выражений (4.6) для gf и ef и несложных тригонометрических преобразований представим в виде φxy(f)=φx(f)-φy(f), то есть является разностью фаз двух спектров.
Как видно из рис. 5б, изменение кросс–фазы носит достаточно случайный характер в связи с влиянием эффектов вытекания мощности, амплитудной модуляции и переходов фазы через границы -180° +180°, что затрудняет ее использование и интерпретацию.
На начальном этапе исследований кросс-фазу как разность фаз двух процессов пытались интерпретировать как индикатор временной задержки в передаче взаимодействия от одного процесса к другому. Однако значимых результатов в этом направлении получено не было, и кросс-фаза в современных исследованиях практически не используется.
Когерентность
Еще одной кросс-спектральной характеристикой является функция когерентности, и именно она практически используется для оценки степени взаимосвязи двух процессов.
Неоднозначность интерпретации
В отношении всех кросс–спектральных характеристик следует особо подчеркнуть, что наличие связи двух процессов могут доказать не результаты проведенного анализа, а только физиологические и анатомические основания. Результаты же анализа могут лишь указать на целесообразность поиска таких оснований.
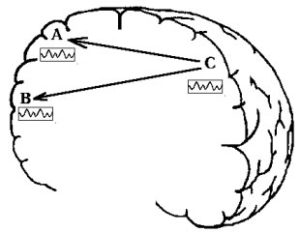
Пусть мы регистрируем ЭЭГ в двух отведениях А и В (рис. 6) и в результате кросс–спектрального анализа обнаруживаем большую аутентичность этих процессов. Однако реально между этими отведениями может не существовать никакой причинной связи, а аутентичность их определена влиянием источника С в другой области головного мозга, анатомически связанного с обоими отведениями А и В.
Обобщенные спектральные показатели
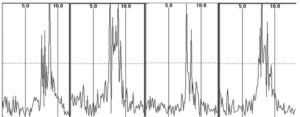
Как было отмечено выше, амплитудный спектр является основной используемой в исследованиях ЭЭГ частотной характеристикой. Однако вследствие погрешностей ДПФ амплитуды отдельных гармоник подвержены влиянию случайных факторов как в отношении их последовательного распределения по частотам, так и на последовательных эпохах анализа (рис. 7).
Тем самым эти амплитуды не могут использоваться в качестве оценочных показателей. Более того, поскольку ЭЭГ не является суммой гармонических колебаний, а нейронные структуры не являются гармоническими осцилляторами, то амплитуды отдельных гармоник лишены физиологического смысла. Поэтому, по крайней мере, в отношении статистической устойчивости более предпочтительно использование усредненных амплитудных и частотных оценок.
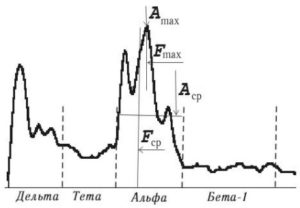
На основе любой спектральной характеристики могут быть вычислены обобщенные спектральные показатели для всех интересующих исследователя частотных диапазонов. В качестве таких показателей в ЭЭГ-анализаторах обычно фигурируют следующие (рис. 8):
![]()
- Аmax — максимальная амплитуда спектра в частотном диапазоне;
- Fmax — частота максимальной по амплитуде гармоники;
- Аср — средняя амплитуда спектра в частотном диапазоне;
- Fcp — средневзвешенная частота, соответствует центру тяжести фигуры, ограниченной кривой спектра в диапазоне, вычисляется по формуле:
где m — число гармоник в частотном диапазоне; F1, Fm — частотные границы диапазона; Аi — амплитуда i-й гармоники;
В исследовательской практике из этих показателей наиболее употребительным является Аср.
Недостатки. Следует отметить, что рассмотренным показателям, как и исходным ненатуральным амплитудным и частотным оценкам ЭЭГ, свойственен ряд погрешностей и случайных флюктуаций, присущих самим частотным характеристикам (см. выше). Поэтому предпочтительнее использовать натуральные оценки периодометрического анализа или огибающей ЭЭГ.
Анализ по эпохам и усреднение спектров
Для исследования временной эволюции спектральных показателей продолжительную ЭЭГ-запись разбивают на последовательные эпохи более короткого размера, на каждой из которых выполняется частотный анализ. Часто для получения более гладких зависимостей от времени эпохи выбирают с определенным взаимным перекрытием (до 50%). Для наглядного визуального представления эволюции избранного показателя обычно используют форму столбиковых диаграмм по эпохам (горизонтальная ось времени) с построением серии диаграмм в порядке отведений. Другим способом представления результатов является серийное топографическое картирование по эпохам или в режиме динамической мультипликации.
Для выявления наиболее стабильных спектральных составляющих на длительных временных интервалах вычисляют усредненные по эпохам частотные характеристики (усреднение производится для каждой спектральной гармоники отдельно).




