Прямой код – это представление числа в двоичной системе счисления, при котором первый (старший) разряд отводится под знак числа. Если число положительное, то в левый разряд записывается 0; если число отрицательное, то в левый разряд записывается 1.
Таким образом, в двоичной системе счисления, используя прямой код, в восьмиразрядной ячейке (байте) можно записать семиразрядное число. Например:
0 0001101 – положительное число
1 0001101 – отрицательное число
Количество значений, которые можно поместить в семиразрядной ячейке со знаком в дополнительном разряде равно 256. Это совпадает с количеством значений, которые можно поместить в восьмиразрядную ячейку без указания знака. Однако диапазон значений уже другой, ему принадлежат значения от -128 до 127 включительно (при переводе в десятичную систему счисления).
При этом в вычислительной технике прямой код используется почти исключительно для представления положительных чисел.
Для отрицательных чисел используется так называемый дополнительный код. Это связано с удобством выполнения операций над числами электронными устройствами компьютера.
Дополнительный код
В дополнительном коде, также как и прямом, первый разряд отводится для представления знака числа. Прямой код используется для представления положительных чисел, а дополнительный – для представления отрицательных. Поэтому, если в первом разряде находится 1, то мы имеем дело с дополнительным кодом и с отрицательным числом.
Все остальные разряды числа в дополнительном коде сначала инвертируются, т.е. заменяются противоположными (0 на 1, а 1 на 0). Например, если 1 0001100 – это прямой код числа, то при формировании его дополнительного кода, сначала надо заменить нули на единицы, а единицы на нули, кроме первого разряда. Получаем 1 1110011. Но это еще не окончательный вид дополнительного кода числа.
Далее следует прибавить единицу к получившемуся инверсией числу:
1 1110011 + 1 = 1 1110100
В итоге и получается число, которое принято называть дополнительным кодом числа.
Причина, по которой используется дополнительный код числа для представления отрицательных чисел, связана с тем, что так проще выполнять математические операции. Например, у нас два числа, представленных в прямом коде. Одно число положительное, другое – отрицательное и эти числа нужно сложить. Однако просто сложить их нельзя. Сначала компьютер должен определить, что это за числа. Выяснив, что одно число отрицательное, ему следует заменить операцию сложения операцией вычитания. Потом, машина должна определить, какое число больше по модулю, чтобы выяснить знак результата и определиться с тем, что из чего вычитать. В итоге, получается сложный алгоритм. Куда проще складывать числа, если отрицательные преобразованы в дополнительный код. Это можно увидеть на примерах ниже.
59 Запись отрицательных чисел, или Дополнительный код
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
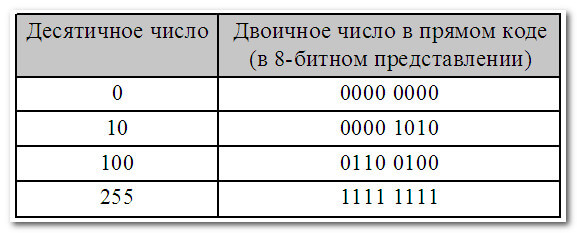
В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
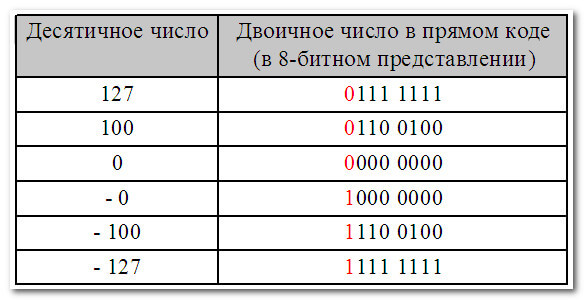
Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0 001 1001
-25= 1 110 0110
и складываем два числа:
0 110 0100 (100) + 1 110 0110 (-25) = 1 0 100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0 100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0 100 1010 + 1 = 0 100 1011 (знаковый бит = 0 , значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0 000 1010
-10= 1 111 0101
и складываем два числа:
0 000 0101 (5) + 1 111 0101 (-10) = 1 111 1010 (знаковый бит = 1 , значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1 111 1010 —-> 1 000 0101
Проверяем:
1 000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Калькулятор дополнительного кода числа
Дополнительный код числа – это способ представления отрицательных чисел в двоичной системе счисления.
Дополнительный код получается путем инвертирования всех битов исходного числа (получение обратного кода) и прибавления единицы к результату.
Этот метод используется в компьютерах для выполнения операций сложения и вычитания.
Наш калькулятор поможет вам быстро и точно рассчитать дополнительный код для любого введенного вами числа.
Просто введите число в соответствующее поле и нажмите кнопку “Рассчитать”.
Результат будет отображен ниже.
Формула для расчета дополнительного кода: (~число + 1 >>> 0).toString(2),
где ~ – это оператор инверсии битов, >>> 0 – это оператор беззнакового сдвига вправо,
который используется для преобразования результата в положительное число,
и .toString(2) – это метод, который преобразует число в строку в двоичной системе счисления.
- Калькулятор прямого и обратного кода двоичного числа
- Калькулятор шестнадцатиричной системы счисления
- Калькулятор перевода из дополнительного кода в десятичный
- Калькулятор перевода систем счисления
- Калькулятор двоичных систем счисления
- Калькулятор умножения в двоичной системе
Прямой, обратный и дополнительный коды
Очень часто в вычислениях должны использоваться не только положительные, но и отрицательные числа.
Число со знаком в вычислительной технике представляется путем представления старшего разряда числа в качестве знакового .
Принято считать, что 0 в знаковом разряде означает знак «плюс» для данного числа, а 1 – знак «минус».

Выполнение арифметических операций над числами с разными знаками представляется для аппаратной части довольно сложной процедурой. В этом случае нужно определить большее по модулю число, произвести вычитание и присвоить разности знак большего по модулю числа.
Применение дополнительного кода позволяет выполнить операцию алгебраического суммирования и вычитания на обычном сумматоре. При этом не требуется определения модуля и знака числа.
Прямой код представляет собой одинаковое представление значимой части числа для положительных и отрицательных чисел и отличается только знаковым битом. В прямом коде число 0 имеет два представления «+0» и «–0».
Обратный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется из прямого кода положительного числа путем инвертирования всех значащих разрядов прямого кода. В обратном коде число 0 также имеет два представления «+0» и «–0».
Дополнительный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется путем прибавления 1 к обратному коду. Добавление 1 к обратному коду числа 0 дает единое представление числа 0 в дополнительном коде. Однако это приводит к асимметрии диапазонов представления чисел относительно нуля.
Так, в восьмиразрядном представлении диапазон изменения чисел с учетом знака.
Таблица прямого, обратного и дополнительного кода 4-битных чисел. Для наглядности представления всего диапазона чисел примем, что сетка представления чисел 4-разрядная, где старший разряд (3) — знаковый, а 0-2 разряды содержат значение числа.
| Число | Прямой код | Обратный код | Дополнительный код |
| -8 | — | — | 1000 |
| -7 | 1111 | 1000 | 1001 |
| -6 | 1110 | 1001 | 1010 |
| -5 | 1101 | 1010 | 1011 |
| -4 | 1100 | 1011 | 1100 |
| -3 | 1011 | 1100 | 1101 |
| -2 | 1010 | 1101 | 1110 |
| -1 | 1001 | 1110 | 1111 |
| 0 0 | 1000 0000 | 1111 0000 | 0000 |
| 1 | 0001 | 0001 | 0001 |
| 2 | 0010 | 0010 | 0010 |
| 3 | 0011 | 0011 | 0011 |
| 4 | 0100 | 0100 | 0100 |
| 5 | 0101 | 0101 | 0101 |
| 6 | 0110 | 0110 | 0110 |
| 7 | 0111 | 0111 | 0111 |
Представление целых чисел в дополнительном коде
Другой способ представления целых чисел — дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal. В других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (-2 15 ) до 32767 (2 15 — 1) и для их хранения отводится 2 байта (16 бит); типа LongInt — в диапазоне от -2 31 до 2 31 — 1 и размещаются в 4 байтах (32 бита); типа Word — в диапазоне от 0 до 65535 (2 16 — 1) (используется 2 байта) и т.д.
Как видно из примеров, данные могут быть интерпретированы как числа со знаком, так и без знака. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если — единицу.
Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.
Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.
Например, если число 37(10) = 100101(2) объявлено величиной типа Integer (шестнадцатибитовое со знаком), то его прямым кодом будет 0000000000100101, а если величиной типа LongInt (тридцатидвухбитовое со знаком), то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричное представление кода. Полученные коды можно переписать соответственно как 0025(16) и 00000025(16).
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
- записать прямой код модуля числа;
- инвертировать его (заменить единицы нулями, нули — единицами);
- прибавить к инверсному коду единицу.
Например, запишем дополнительный код числа -37, интерпретируя его как величину типа LongInt (тридцатидвухбитовое со знаком):
- прямой код числа 37 есть 00000000000000000000000000100101;
- инверсный код 11111111111111111111111111011010;
- дополнительный код 11111111111111111111111111011011 или FFFFFFDB(16).
бным). Под точкой здесь подразумевается знак-разделитель целой и дробной части числа.
1) Представление целых чисел
Множество целых чисел, представленных в памяти ЭВМ, ограничено. Диапазон значений зависит от размера ячеек памяти, используемых для их хранения. Для целых чисел существуют два представления: -беззнаковое; -со знаком.
В К-разрядной ячейке может храниться 2 к различных значений целых чисел.
Диапазон значений целых беззнаковых чисел (только положительные): от 0 до 2 к — 1 для 16-разрядной ячейки от 0 до 65535 для 8-разрядной ячейки от 0 до 255
Диапазон значений целых чисел со знаком (и отрицательные, и положительные в равном количестве): от -2 к-1 до 2 к-1 -1 для 16-разрядной ячейки от -32768 до 32767 для 8-разрядной ячейки от -128 до 127
Чтобы получить внутреннее представление целого положительного числа N, хранящегося в К-разрядной ячейке, необходимо: 1. перевести число N в двоичную систему счисления; 2. полученный результат дополнить слева незначащими нулями до К разрядов.
Получить внутреннее представление целого числа 1607 в 2-х байтовой ячейке.
Решение: N=1607=110010001112. Внутреннее представление этого числа будет: 0000 0110 0100 0111. Шестнадцатеричная форма внутреннего представления числа: 0647.
Алгоритм представления целого положительного числа в компьютере в двух байтовом формате
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Число двоичных разрядов
Рассчитать
Представление положительного числа
Обратный код
Дополнительный код
Ссылка Сохранить Виджет
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А это все для удобной работы со знаками. Поскольку я все люблю понимать на примерах, рассказывать я тоже буду на примерах. Итак, предположим, что у нас 4 разряда для работы с двоичными числами. Представить таким образом можно 16 чисел — 0, 1, . 15
00 — 0000
.
15 — 1111
Но если нет знака, убогая получается арифметика. Нужно вводить знак. Чтобы никого не обидеть, половину диапазона отдадим положительным числам (8 чисел), половину — отрицательным (тоже 8 чисел). Ноль, что отличает машинную арифметику от обычной, мы отнесем в положительные числа (в обычной арифметике у нуля нет знака, если не ошибаюсь). Итого, в положительные числа попадают 0. 7, а в отрицательные -1, . -8.
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
Вот для их представления как раз и используется дополнительный код.
То есть, -7 в дополнительном коде получается так
прямой код 7 = 0111
обратный код 7 = 1000
дополнительный код 7 = 1001
Обратим внимание на то, что прямой код 1001 представляет число 9, которое отстоит от числа -7 ровно на 16, или .
Или, что тоже самое, дополнительный код числа «дополняет» прямой код до , т.е. 7+9=16
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
P.S. Ну а обратный код дополняет число до , или до всех 1, потому и называется дополнением до 1. Им тоже можно представлять отрицательные числа, и реализовать вычитание и сложение схемой сложения, только сложение там хитрее — с циклическим переносом, ну и представить можно меньше на одно число, так как все единицы уже заняты — это обратный код нуля, эдакий «минус нуль», то есть диапазон получается, если брать наш пример от -7 до 7. Не так удобно, одним словом.
▍ Построение таблицы в Commodore BASIC
Commodore BASIC обрабатывает знаковые и беззнаковые числа внутренне. Но не может же статья на этом сайте (речь об imapenguin.com, — прим. пер.) обойтись без винтажного ПК?
Посмотрим, как это реализуется на Commodore 128 (должно работать на многих диалектах BASIC из начала 80-х):
2 PRINTCHR$(147) 3 PRINT»TWOS COMPLEMENT CHART FOR 8 BIT VALUES» 4 PRINT»—————————————-» 5 PRINT»POSITIVE NEGATIVE UNSIGNED BINARY» 10 FOR N=0TO127 30 T=0 40 FOR I=0 TO 7 50 B=2^I 60 IF (N AND B) = B THEN GOTO80 70 T=T+B 80 NEXT I 90 T=(T+1) AND 255 100 PRINT N,-N,T, 120 FOR I=7 TO 0 STEP -1 130 B=2^I 140 IF (T AND B) = B THEN PRINT «1»;:GOTO 150 145 PRINT «0»; 150 NEXT I 160 PRINT 170 NEXT
Интересно. В документации Commodore операция AND называется логическое AND . Но эту операцию можно использовать для проверки установки битов, значит, в правильных руках она будет побитовым AND .

Версия на ППВМ
Нет макетной платы – нет проблем. Вполне будет достаточно вашей карманной ППВМ.
У вас же припасена в кармане ППВМ, не так ли?
Дополнительный код на ППВМ реализуется легко. Вот пример модуля, получающего 8-битный ввод и выдающего его дополнительный код:
module TwosComplement( input [7:0] in, // 8-битный ввод output [7:0] out // 8-битный вывод, представляющий дополнительный код ); // Инвертирование всех битов входного значения; равнозначно работе наших вентилей XOR на микросхеме 74LS86 wire [7:0] inverted; assign inverted = ~in; // Прибавление 1 к инвертированному вводу; равнозначно работе сумматоров на нашей 74LS283 assign out = inverted + 1; endmodule
Поскольку ширина регистров 8 бит, эти операции будут циклически обнуляться и работать для всех 8-битных целых чисел. Как и ассемблер, ППВМ не интересует, используете вы знаковое или беззнаковое число. Вы сами должны подобрать для него правильную реализацию.
Также, если возникнет потребность поработать с обратным кодом, можете просто использовать этот инвертированный сигнал.
Преимущества и недостатки
Преимущества
- Один и тот же регистр может хранить как n-битовое положительное число, так и (n−1)-битовое число со знаком, с общими для обоих форматов операциями сложения, вычитания и левого сдвига.
- Более удобная упаковка чисел в битовые поля.
- Отсутствие числа «минус ноль».
Недостатки
- Дополнительный код неочевиден для новичков.
- В сложных форматах (таких, как плавающая запятая или двоично-десятичный код) большинство преимуществ аннулируются.
- Модуль наибольшего числа не равен модулю наименьшего числа. Пример: знаковое целое 1-байтовое. Максимальное число: 12710 == 7F16 == 011111112. Минимальное число: -12810 == 8016,дополнительный код == 100000002,дополнительный код. Соответственно, не для любого числа существует противоположное. Операция изменения знака требует дополнительной проверки.
Пример программного преобразования
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными.
C# .NET / C style
byte b1 = 254; //11111110 (бинарное) byte b2 = 121; //01111001 (бинарное) int c = (int)Math.Pow(2,(sizeof(byte)*8)-1); //2 возводится в степень 7. Результат: 10000000 (бинарное) int b1Conversion=(c ^ b1) — c; //Результат: -2. А фактически, двоичный дополнительный код. int b2Conversion=(c ^ b2) — c; //Результат остаётся 121, потому что знаковый разряд — нуль.




