Закон ома для полной цепи формула и определение

Содержание

Признаком классификации участков электрического контура на однородные и неоднородные является отсутствие или наличие соответственно источников тока, которые характеризуются физическим параметром — электродвижущей силой (varepsilon) (далее — ЭДС ):

(boxed>>), ((1))
где (A_) — отличная от нуля работа сторонних (не электростатических, не потенциальных) сил,
(q_0 = 1) Кл и (q_0 > 0).

Обрати внимание!

Размерность ЭДС: [(varepsilon)] (= 1 В=1 frac<Дж>).
Размерность потенциала: [(varphi)] (= 1 В=1 frac<Дж>).
Размерность напряжения: [(U)] (= 1 В=1 frac<Дж>).

При рассмотрении неоднородного участка цепи физическое понятие «напряжение» обобщается:
1) для однородного участка цепи (наличие только (R) (активного сопротивления) или (C) (конденсатора):
(U = varphi_ <(+)>- varphi_ = varphi_1 — varphi_2,) ((2))
где (varphi_ <(+)>> varphi_) (ток «течёт» от большего потенциала к меньшему);
2) для неоднородного участка цепи (1)–(2) (наличие (R), (r) и (varepsilon)):
(U = (varphi_1 — varphi_2) pm varepsilon_), ((3))
где (r) — внутреннее сопротивление источника тока и

знак (varepsilon_<12>) определяется знаком работы, совершаемой сторонними силами в направлении (1)–(2).

Формулировка и объяснение закона Ома

Немец Георг Ом изучал фичи электричества в 19 веке, и стал таким великим физиком, что в честь него теперь законы называют. И не зря. Это мы уже хорошо знакомы с ним и его возможностями, потому что он есть в каждом доме. А тогда люди только начали изучать движение частиц, и не все было так очевидно. Поэтому наш ученый долго следил за потоком частиц и вывел закономерности.

В такой форме закон Ома дошел до наших дней: сила тока через участок цепи прямо пропорциональна напряжению на этом участке и обратно пропорциональна сопротивлению этого участка.

Это значит, что здесь линейная зависимость: при увеличении напряжения, увеличится сила потока и наоборот.

Формула: I = U / R,

где I — сила тока, U — напряжение, R — сопротивление.

Это правило может применяться далеко не для всех условий. Оно характерно для постоянного тока, для переменного используются другие понятия. Но в ОГЭ и ЕГЭ тебе точно встретятся задачи, для решения которых придется вспомнить об этой зависимости.

Закон Ома для участка цепи

Проверим твою внимательность: заметил, что в самом определении закона Ома используется термин «участок цепи»?

Закон Ома для полной цепи и участка цепи. Объяснение смысла и применения простым языком.

Определние, которое мы приводили выше, и является законом Ома для участка цепи.

Что такое этот загадочный участок? Это часть электросхемы, которая содержит определенный набор элементов. В этой части мы и будем проводить наши изменения и вычисления, не обращая внимания на другие условия.

Когда мы имеем дело с таким отдельно взятым участком, смело можем использовать выражение, которое, надеемся, ты запомнил.

Последовательное соединение

Последовательным называется соединение, при котором каждый проводник соединяется только с одним предыдущим и одним последующим проводниками.

Как следует из первого правила Кирхгофа, при последовательном соединении проводников сила электрического тока, протекающего по всем проводникам, одинакова (на основании закона сохранения заряда).

1. При последовательном соединении проводников (рис. 1) сила тока во всех проводниках одинакова: I1 = I2 = I3 = I

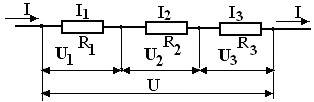
Рис. 1. Последовательное соединение двух проводников.

2. Согласно закону Ома, напряжения U1 и U2 на проводниках равны U1 = IR1, U2 = IR2, U3 = IR3.

Напряжение при последовательном соединении проводников равно сумме напряжений на отдельных участках (проводниках) электрической цепи.

U = U1 + U2 + U3

По закону Ома, напряжения U1, U2 на проводниках равны U1 = IR1, U2 = IR2, В соответствии вторым правилом Кирхгофа напряжение на всем участке:

U = U1 + U2 = IR1+ IR2 = I(R1+ R2)= I·R. Получаем: R = R1 + R2

Общее напряжение U на проводниках равно сумме напряжений U1, U2 ,U3 равно: U = U1 + U2 + U3 = I·(R1 + R2 + R3) = IR

где RЭКВ – эквивалентное сопротивление всей цепи. Отсюда: RЭКВ = R1 + R2 + R3

При последовательном соединении эквивалентное сопротивление цепи равно сумме сопротивлений отдельных участков цепи: R ЭКВ= R1 + R2 + R3+…

Этот результат справедлив для любого числа последовательно соединенных проводников.

Из закона Ома следует: при равенстве сил тока при последовательном соединении:

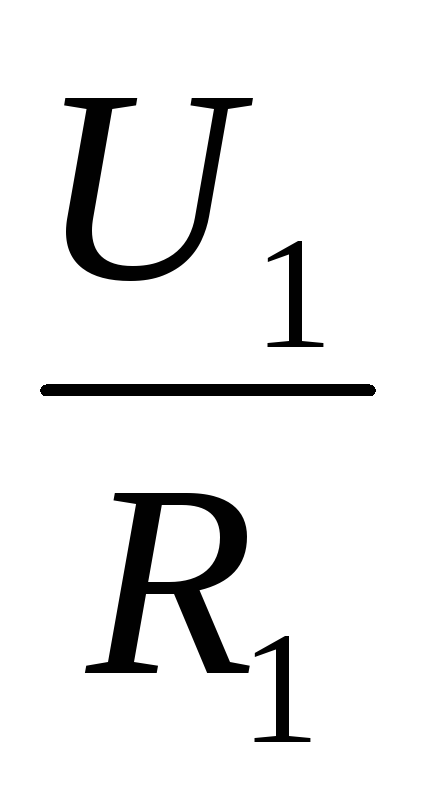I = ,I = . Отсюда 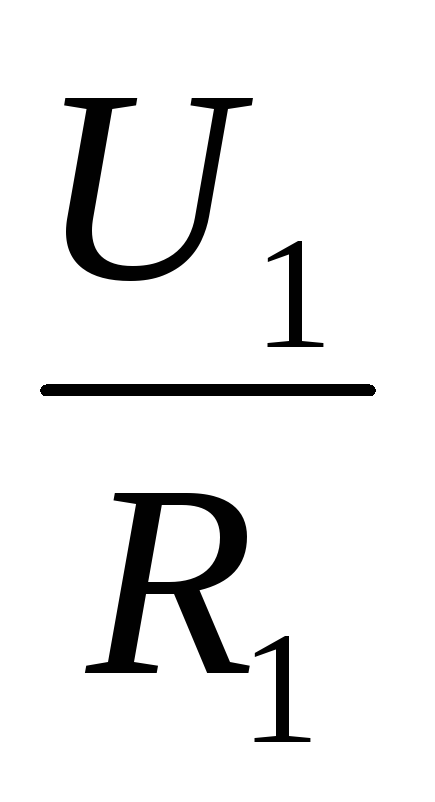= 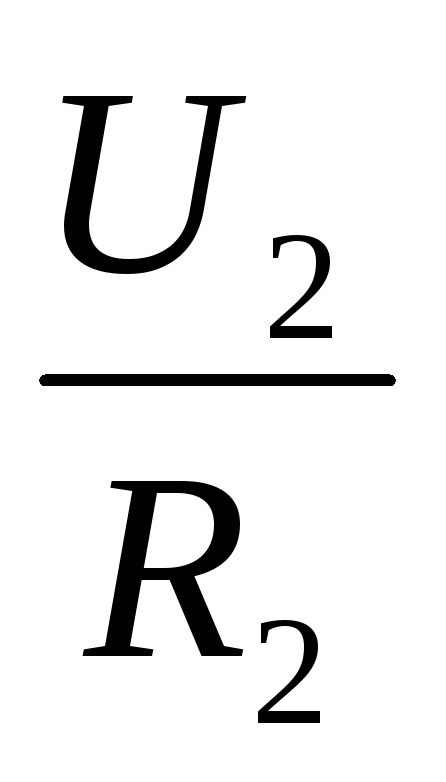или 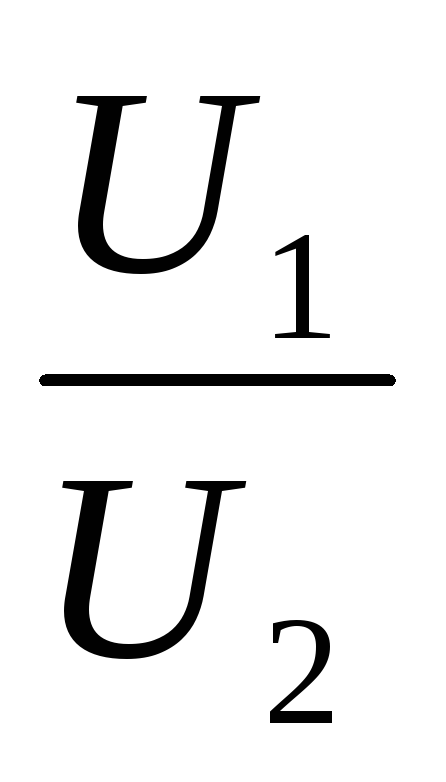=, т. е. напряжения на отдельных участках цепи прямо пропорциональны сопротивлениям участков.

При последовательном соединении n одинаковых проводников общее напряжение равно произведению напряжению одного U1 на их количество n:

UПОСЛЕД= n ·U1. Аналогично для сопротивлений: RПОСЛЕД = n· R1

При размыкании цепи одного из последовательно соединенных потребителей ток исчезает во всей цепи, поэтому последовательное соединение на практике не всегда удобно.

Вывод формул закона Ома

Вывод формулы закона Ома для участка цепи можно провести на основе закона Джоуля-Ленца. Этот закон гласит, что количество теплоты Q, выделяющееся на участке цепи, пропорционально квадрату силы тока I, сопротивлению участка R и времени прохождения тока t:

С другой стороны, по закону сохранения энергии выделившаяся на участке теплота Q равна работе A тока на преодоление напряжения U:

Приравнивая два выражения для Q и решая полученное уравнение относительно I, получаем формулу закона Ома для участка цепи:

Аналогично можно вывести формулу закона Ома для полной цепи, основываясь на законе Джоуля-Ленца для полной цепи:

Решая это уравнение относительно I, окончательно получаем:

Таким образом, используя более общие законы физики, можно строго математически получить основные формулы закона Ома, выражающие связь между током, напряжением и сопротивлением.

Графическая интерпретация закона Ома

Закон Ома для участка цепи можно проиллюстрировать с помощью так называемого треугольника Ома:

Этот треугольник наглядно демонстрирует связь между током I, напряжением U и сопротивлением R:

ток I пропорционален напряжению U и обратно пропорционален R;
если U растёт, то растёт и I;
если R растёт, то I уменьшается.

Треугольник Ома наглядно демонстрирует качественную зависимость между величинами, о которой говорит закон Ома. Это помогает лучше понять физический смысл закона.

Далее рассмотрим примеры применения закона Ома для расчёта электрических цепей.

Закон Ома для полной цепи

Когда в полной электрической цепи имеется источник ЭДС, в цепи возникает ток. Его величину можно найти, используя закон сохранения энергии и закон Джоуля-Ленца, выражающий энергию, выделяемую на электрическом элементе при прохождении по нему тока.

Если сторонние силы за время $Δt$ переместили заряд $Δq$, то, они совершили работу:

Заряд, переносимый сторонними силами внутри источника, пройдет по цепи за то же время $Δt$, а значит, сила тока в цепи будет равна:

Таким образом, величина работы сторонних сил:

А согласно закону Джоуля-Ленца, ток $I$, прошедший через цепь, создаст некоторое количество теплоты. Во внешней цепи эта теплота выделится на сопротивлении внешней цепи $R$, а внутри источника тока – на его внутреннем сопротивлении $r$:

Вся эта теплота, согласно Закону сохранения энергии, получена в результате работы сторонних сил ($А_ = Q$), то есть:

Сокращая и перенося значение тока влево, окончательно получаем формулу Закона Ома для полной цепи:

Сила тока в замкнутой цепи равна отношению ЭДС источника тока к сумме сопротивления цепи и внутреннего сопротивления источника.

Внутреннее сопротивление реальных источников тока очень невелико (доли ома), поэтому для небольших мощностей оно почти не оказывает влияния на электрическую цепь. Однако, если мощность цепи велика, то пренебрегать этим сопротивлением нельзя, на нем может выделяться заметное количество тепла.

Сложные цепи с несколькими источниками тока

В замкнутой цепи может быть не один источник тока.

В этом случае полная ЭДС цепи равна алгебраической сумме ЭДС источников. В цепи произвольно выбирается направление обхода, и если источник вызывает ток в этом направлении, его ЭДС считается положительной, а иначе – отрицательной. Сопротивление не имеет направления, а поэтому внешние и внутренние сопротивления всегда суммируются.

В реальных сложных электрических цепях может быть много разветвлений и контуров, причем, источники тока могут находиться в различных местах. Для определения токов на всех ветвях цепи используются системы уравнений, построенные на основе специальных правил (законов) Кирхгофа.

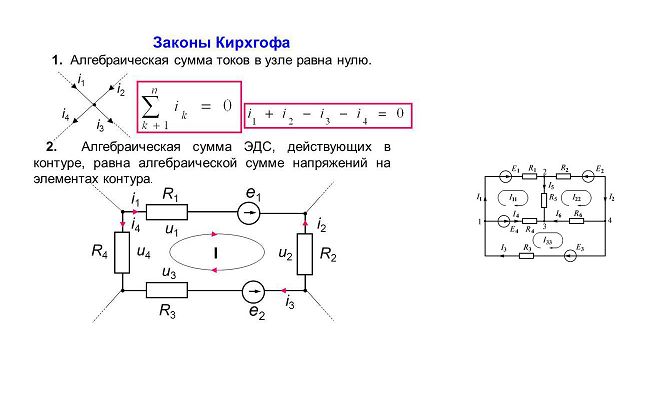
Отдельный участок и полная электрическая цепь

Рассматривая электрическую цепь с точки зрения применения к схеме закона Ома, следует отметить два возможных варианта расчета: для отдельно взятого участка и для полноценной схемы.

Расчет тока участка электрической схемы

Участком электрической цепи, как правило, рассматривается часть схемы, исключающая источник ЭДС, как обладающий дополнительным внутренним сопротивлением.

Поэтому расчетная формула, в данном случае, выглядит просто:

I = U/ R,

Трактовка формулы простая – ток, протекающий по некоему участок цепи, пропорционален приложенному к нему напряжению, а сопротивлению – обратно пропорционален.

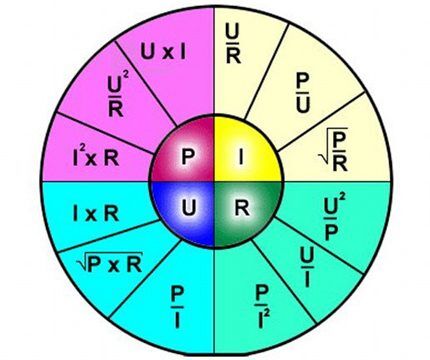
Так называемая графическая «ромашка», посредством которой представлен весь набор вариаций формулировок, основанных на законе Ома. Удобный инструмент для карманного хранения: сектор «P» — формулы мощности; сектор «U» — формулы напряжения; сектор «I» — формулы тока; сектор «R» — формулы сопротивления

Таким образом, формулой чётко описывается зависимость протекания тока по отдельному участку электрической цепи относительно определенных значений напряжения и сопротивления.

Формулой удобно пользоваться, например, рассчитывая параметры сопротивления, которое требуется впаять в схему, если заданы напряжение с током.

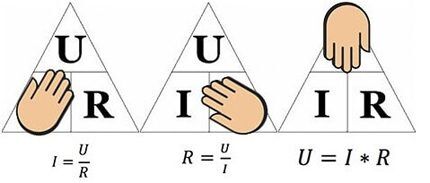
Закон Ома и два следствия, которыми необходимо владеть каждому профессиональному электромеханику, инженеру-электрику, электронщику и всем, кто связан с работой электрических цепей. Слева направо: 1 — определение тока; 2 — определение сопротивления; 3 — определение напряжения, где I — сила тока, U — напряжение, R — сопротивление

Вышеприведенный рисунок поможет определить, например ток, протекающий через 10-омное сопротивление, к которому приложено напряжение 12 вольт. Подставив значения, найдем – I = 12 / 10 = 1.2 ампера.

Аналогично решаются задачи поиска сопротивления (когда известны ток с напряжением) или напряжения (когда известны напряжение с током).

Тем самым всегда можно подобрать требуемое рабочее напряжение, нужную силу тока и оптимальный резистивный элемент.

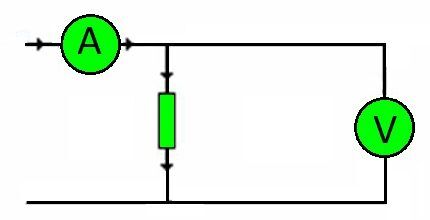
Формула, которой предложено пользоваться, не требует учитывать параметры источника напряжения. Однако, схема, содержащая, например, аккумулятор, будет рассчитываться по другой формуле. На схеме: А – включение амперметра; V – включение вольтметра.

Кстати, соединительные провода любой схемы – это сопротивления. Величина нагрузки, которую им предстоит нести, определяется напряжением.

Соответственно, опять же пользуясь законом Ома, становится допустимым точный подбор необходимого сечения проводника, в зависимости от материала жилы.

У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.

Вариант расчета для полной цепи

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС.

Поэтому логичным является некоторое изменение выше рассмотренной формулы:

I = U / (R + r)

Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС.

Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.

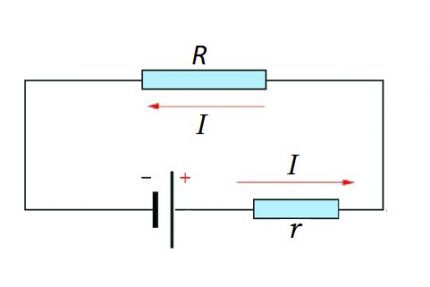
Для расчетов в условиях полноценной электрической цепи всегда берется к учету резистивное значение источника ЭДС. Это значение суммируется с резистивным сопротивлением непосредственно электрической цепи. На схеме: I — прохождение тока; R — резистивный элемент внешний; r — резистивный фактор ЭДС (источника энергии)

Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины.

Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.

Рассмотрение действия закона к переменной величине

Понятие «сопротивление» к условиям прохождения переменного тока следует рассматривать уже больше как понятие «импеданса». Здесь имеется в виду сочетание активной резистивной нагрузки (Ra) и нагрузки, образованной реактивным резистором (Rr).

Обусловлены подобные явления параметрами индуктивных элементов и законами коммутации применительно к переменной величине напряжения — синусоидальной величине тока.

Такой видится эквивалентная схема электрической цепи переменного тока под расчет с применением формулировок, исходящих из принципов закона Ома: R — резистивная составляющая; С — емкостная составляющая; L — индуктивная составляющая; ЭДС -источник энергии; I -прохождение тока

Другими словами, имеет место эффект опережения (отставания) токовых значений от значений напряжения, что сопровождается появлением активной (резистивной) и реактивной (индуктивной или емкостной) мощностей.

Расчёт подобных явлений ведётся при помощи формулы:

Z = U / I или Z = R + J * (XL — XC)

где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.

Последовательное и параллельное включение элементов

Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.

Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.

Цепь последовательно включенных резистивных элементов

Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:

Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.

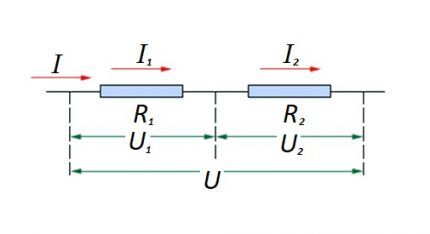
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U, U1, U2 — приложенное напряжение

Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.

При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.

Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.

Цепь параллельно включенных резистивных элементов

На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:

Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.

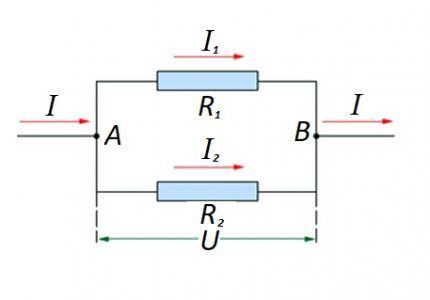
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 — прохождение тока; R1, R2 — резистивные элементы; U — подведённое напряжение; А, В — точки входа/выхода

Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.

Интегральная и дифференциальная формы закона

Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.

Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.

Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.

Под дифференциальный расчет берется формула: J = ό * E

Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ

Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.

Пример

Представим схему с источником энергии и с лампочкой. И следуем закону Ома.

Если мы увеличим напряжение, то лампочка будет светиться ярче, ведь сила потока зарядов увеличится. Если же у нас будет лампочка с большим сопротивлением, то она будет светиться слабее.