На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
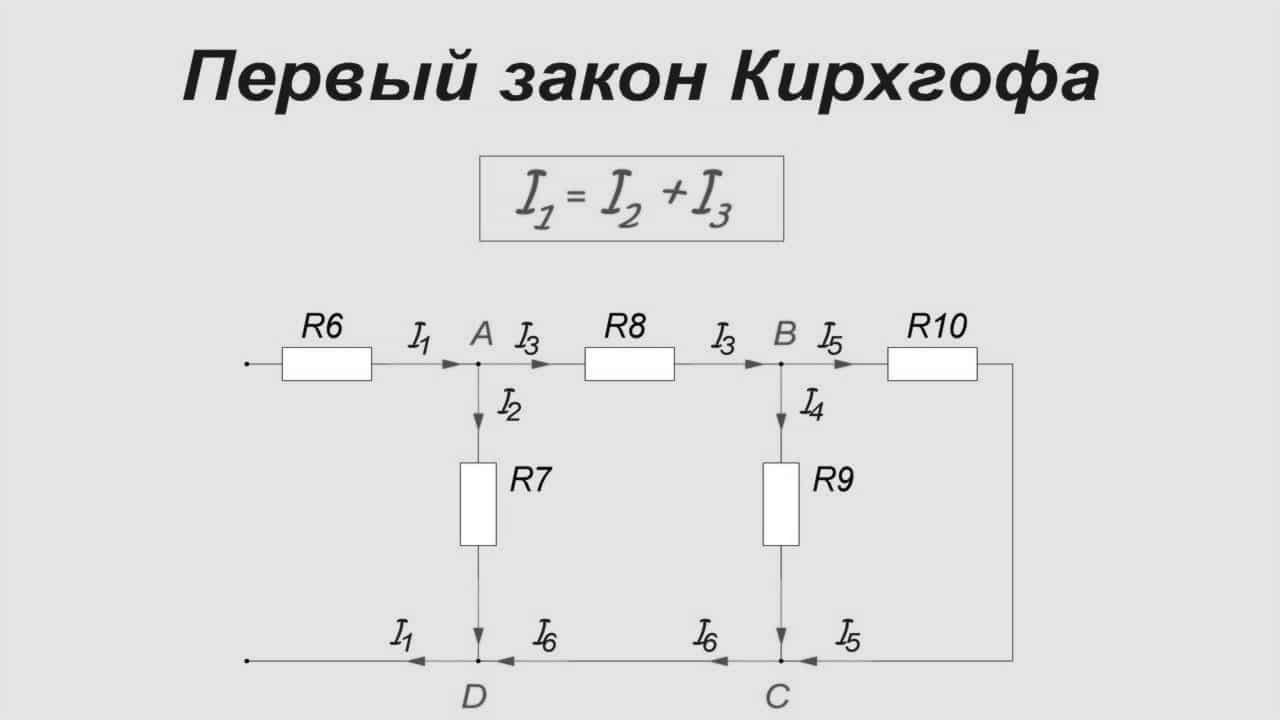
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Применение законов Кирхгофа при решении задач
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.
Здесь ток I1 — ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I 3 в левую часть выражения (1), тем самым получим:
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
— напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
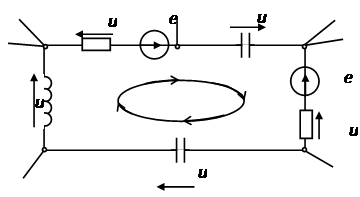
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Определение второго закона Кирхгофа
Второй закон Кирхгофа, также известный как закон о законах узлов или закон о законах токов, является одним из основных законов электрических цепей. Он устанавливает, что сумма токов, втекающих в узел, равна сумме токов, вытекающих из узла.
Формально, второй закон Кирхгофа можно записать следующим образом:
Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла:
где ∑ обозначает сумму, Iвтек – ток, втекающий в узел, и Iвытек – ток, вытекающий из узла.
Второй закон Кирхгофа основан на законе сохранения заряда, который утверждает, что заряд не может создаваться или исчезать внутри электрической цепи. Таким образом, сумма токов, втекающих в узел, должна быть равна сумме токов, вытекающих из узла, чтобы сохранить баланс заряда.
Формулировка второго закона Кирхгофа
Второй закон Кирхгофа, также известный как закон о балансе токов в узле, утверждает, что сумма токов, втекающих в узел, должна быть равна сумме токов, вытекающих из узла.
Формально, второй закон Кирхгофа может быть сформулирован следующим образом:
где ∑ обозначает сумму, Iвтек – ток, втекающий в узел, и Iвытек – ток, вытекающий из узла.
Этот закон основан на законе сохранения заряда, который утверждает, что заряд не может создаваться или исчезать внутри электрической цепи. Таким образом, сумма токов, втекающих в узел, должна быть равна сумме токов, вытекающих из узла, чтобы сохранить баланс заряда.
Законы Кирхгофа простыми словами
Два закона Кирхгофа вместе с законом Ома составляют тройку законов, с помощью которых можно определить параметры электрической цепи любой сложности. Законы Кирхгофа мы будем проверять на примерах простейших электрических схем, собрать которые не составит никакого труда. Для этого понадобится несколько резисторов, пара источников питания, в качестве которых подойдут гальванические элементы (батарейки) и мультиметр.
Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.
Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.
Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.
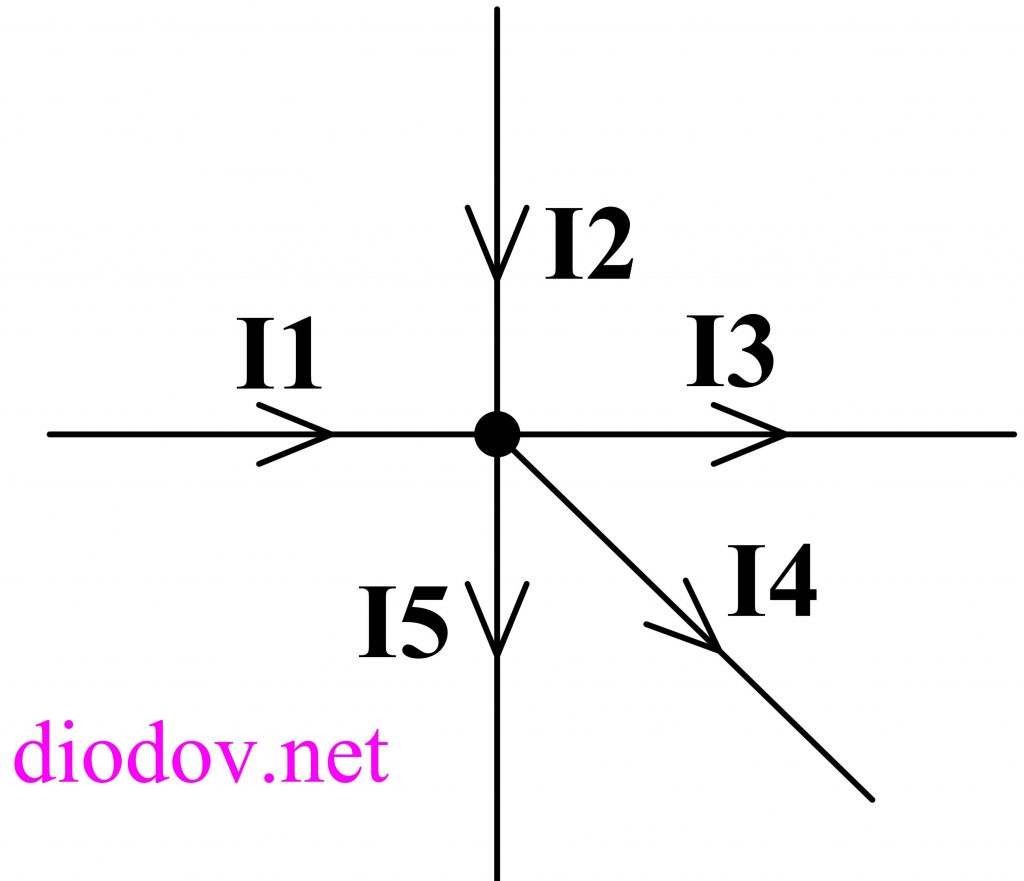
Согласно первому закону Кирхгофа
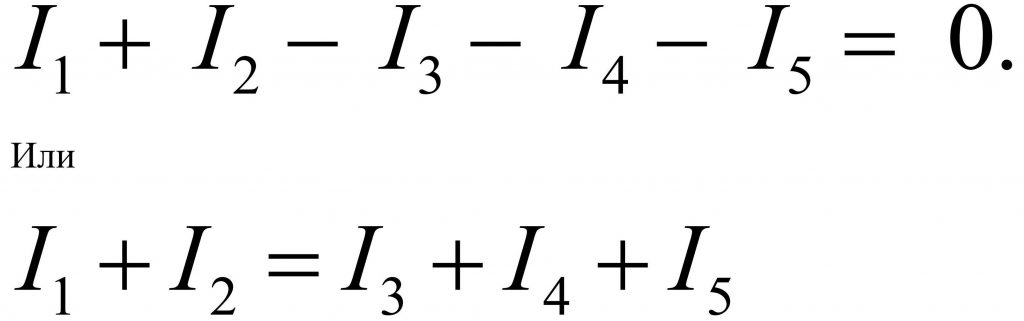
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.
1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.
Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.
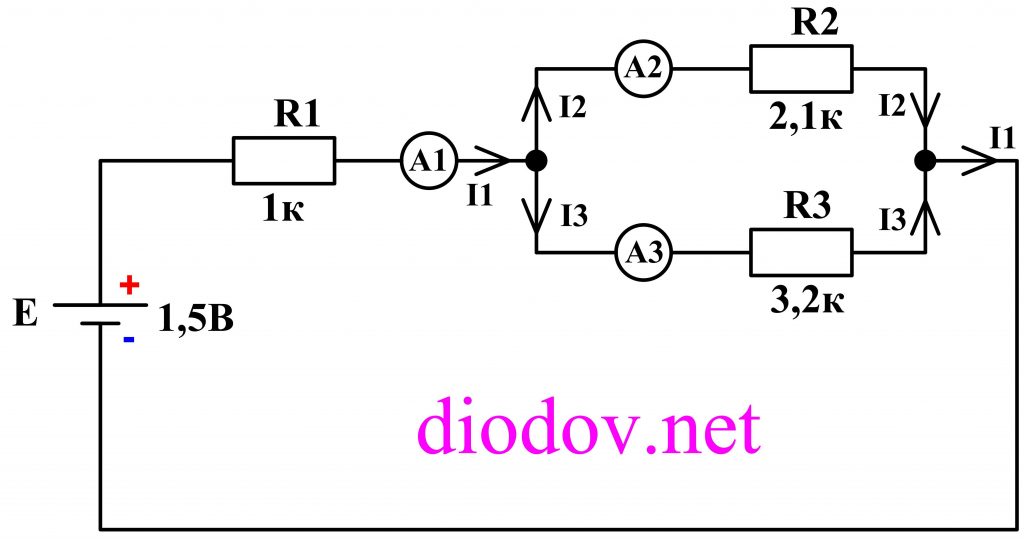
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:
Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.
Второй закон Кирхгофа
Второй закон Кирхгофа воспринимается начинающими радиолюбителями гораздо сложнее, нежели первый. Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.
Упрощенно 2 закон Кирхгофа говорит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений
ΣE = ΣIR
Самый простой случай данного закона разберем на примере батарейки 1,5 В и одного резистора.
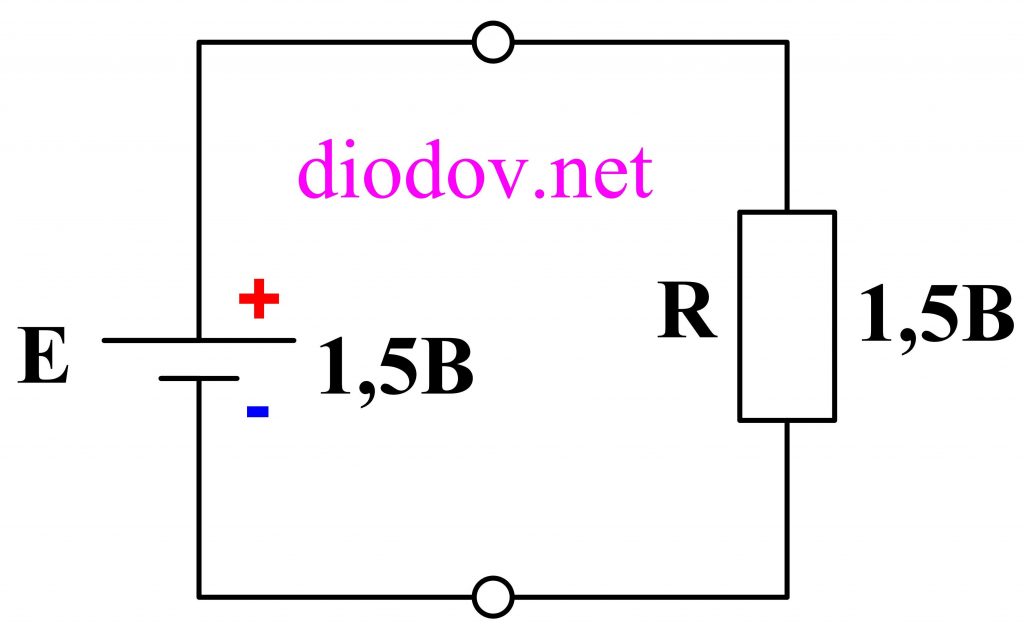
Поскольку резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.
Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, то есть по 0,75 В.
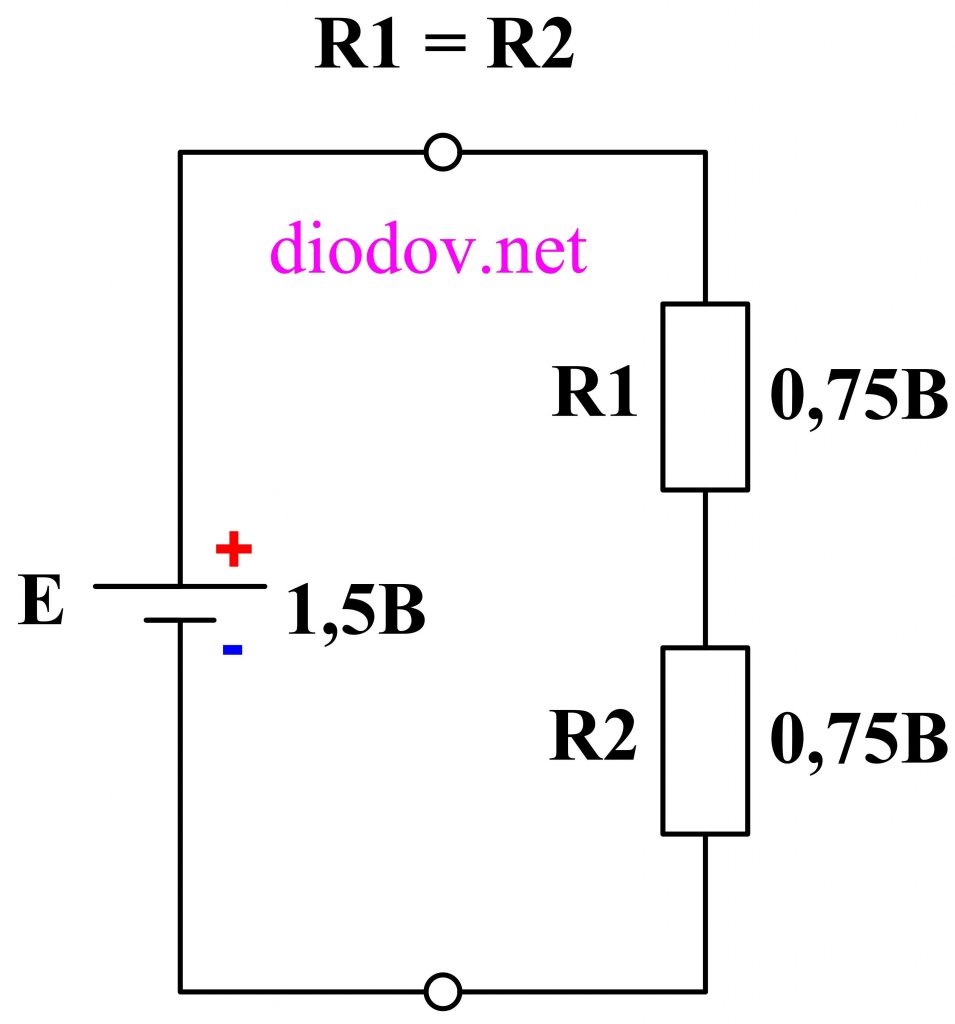
Если возьмем три резистора снова одинакового номинала, например по 1 кОм, то падение напряжения на них будет по 0,5 В.
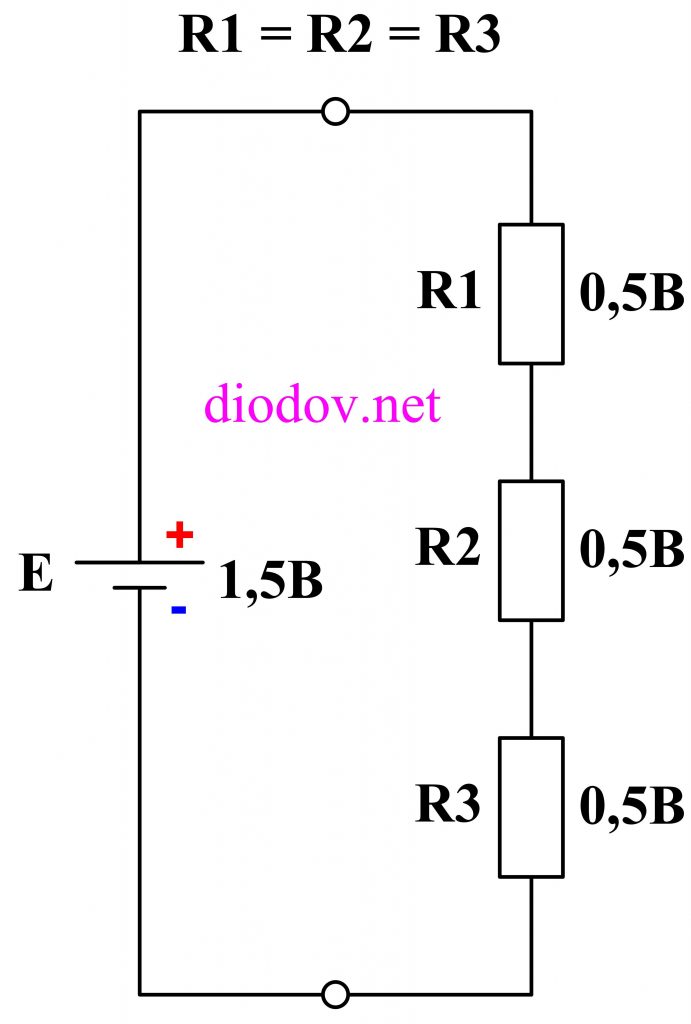
Формулой это будет записано следующим образом:
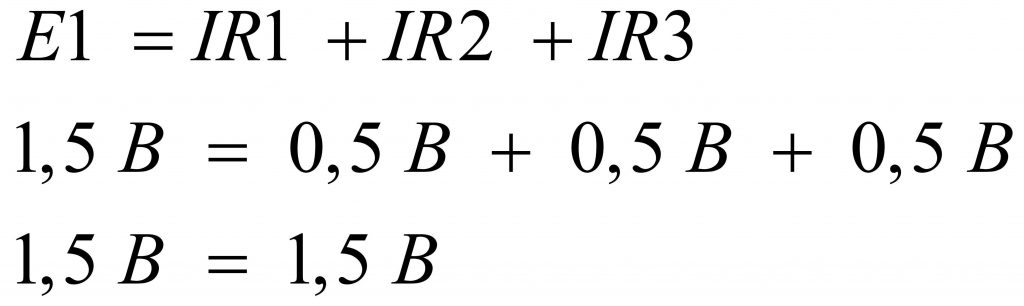
Рассмотрим условно более сложный пример. Добавим в последнюю схему еще один источник питания E2, напряжением 4,5 В.
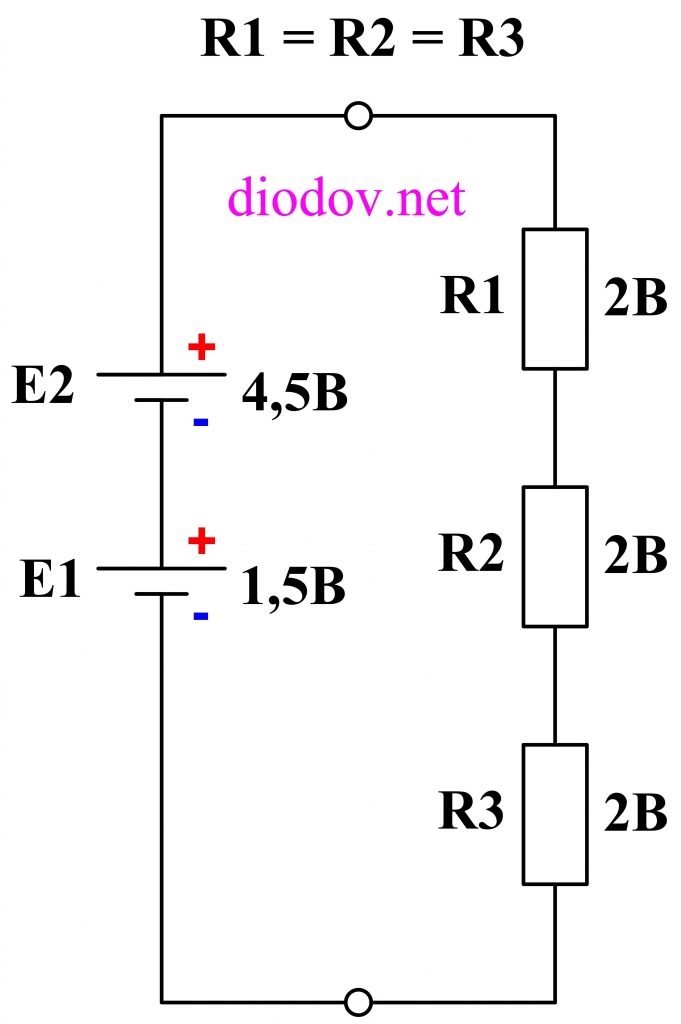
Обратите внимание, что оба источника соединены последовательно и согласно, то есть плюс одной батарейки соединяется с минусом другой батарейки или наоборот. При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:
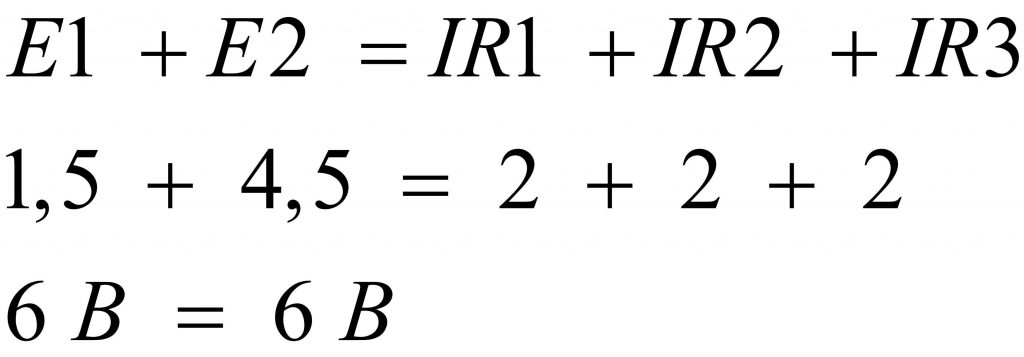
И последний отличительный вариант, который мы рассмотрим в данной статье, предполагает последовательное встречное соединение гальванических элементов. При таком соединении источников питания из большей ЭДС отнимается значение меньшей ЭДС. Следовательно к резисторам R1…R3 будет приложена разница E1 – E2, то есть 4,5 – 1,5 = 3 В, — по одному вольту на каждый резистор.
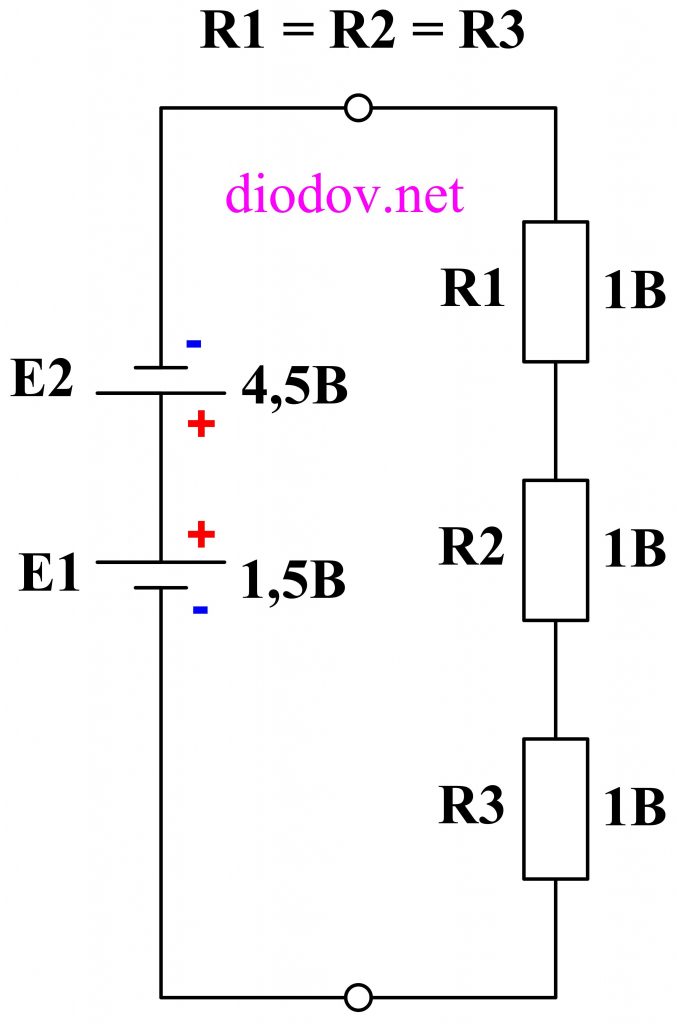
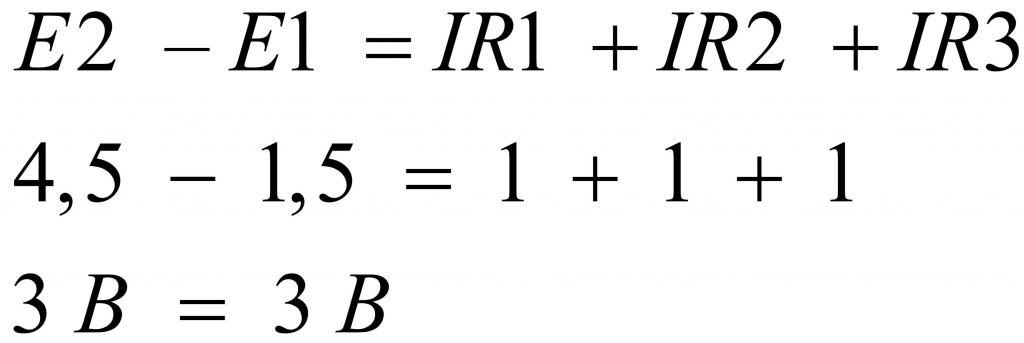
Второй закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, а также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить соответствующие измерения с помощью мультиметра.
Законы Кирхгофа действуют как для постоянного, так и для переменного тока.
Законы Кирхгофа: решение задач

Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.

Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа . В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три, независимых из них только два. Третий контур включает в себя все остальные и не может считаться независимым. И вообще всегда при всех расчетах мы должны использовать только независимые контура. Не поддавайтесь искушению записать еще одно уравнение за счет этого общего контура, ничего хорошего не выйдет .
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I1, I2, I3.
Мы видим, что в контуре №1 направление токов I1 и I3, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I2 совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I3 направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:

А теперь запишем этот же закон для контура №2:

Видим, что в контуре №2 нет источников питания, поэтому в левой части (где у нас согласно второму закону Кирхгофа стоит сумма ЭДС) у нас нолик. Итак, у нас есть два уравнения, а неизвестных-то у нас три (I1, I2, I3). А нам известно, что для нахождения трех неизвестных нужна система с тремя независимыми уравнениями. Где же взять третье недостающее уравнение? А, например, из первого закона Кирхгофа ! Согласно этому закону мы можем записать

Господа, теперь полный порядок, у нас есть три уравнения и три неизвестных и нам остается только решить вот такую вот систему уравнений

Подставим конкретные числа. Все расчеты будем вести в кошерной системе СИ. Рекомендую всегда считать только в ней. Не поддавайтесь искушению подставлять куда-то миллиметры, мили, килоамперы и прочее. Возможно возникновение путаницы.

Решение таких систем рассматривается чуть ли не в начальной школе и, полагаю, не должно вызывать трудностей . Если что, есть куча математических пакетов, которые сделают это за вас, если вам лень самим ручками считай. Поэтому мы опустим процесс решения, а сразу приведем результат

Видим, что все токи получились у нас со знаком плюс. Это значит, что мы верно угадали их направление. Да, то есть токи в схеме текут именно в том направлении, как мы нарисовали стрелочки на рисунке 1. Однако из условия задачи необходимо найти не только токи через резисторы, но и падение напряжения на них. Как это сделать? Например, с помощью уже изученного нами закона Ома . Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление. Поэтому, используя вот эту формулу

находим напряжение на каждом резисторе

Заметим, господа, что напряжения на резисторах R2 и R3 равны между собой. Это и логично, поскольку они соединены между собой параллельно. Однако пока не будем на этом акцентировать большое внимание, рассмотрим это лучше в другой раз.
Итак, господа, мы решили эту простую задачку с помощью двух законов Кирхгофа и закона Ома . Но это был совсем простой пример. Давайте попробуем решить более сложную задачу. Взгляните на рисунок 2.

Рисунок 2 – Схема посложнее
Схема выглядит внушительно, не правда ли? Возможно, вам даже не верится, что эту схему можно легко рассчитать. Однако, господа, уверяю вас, вы обладаете всеми необходимыми знаниями для расчета этой схемы, если уже изучили мои предыдущие статьи. Сейчас вы в этом убедитесь.
Для начала зададимся конкретными цифрами значений сопротивлений резисторов и напряжений источников.
Пусть Е1=15 В, Е2=24 В, R1= 10 Ом, R2 = 51 Ом, R3=100 Ом, R4=1 кОм, R5=10 Ом, R6=18 Ом, R7=10 кОм.
Найти, как и в прошлой задаче, требуется все токи в схеме и напряжения на всех резисторах.
В этой схеме мы можем видеть три независимых контура. Обозначим их римскими цифрами I, II, III. В каждом контуре зададимся направлением обхода. Они показаны синими стрелками.
Дальше как и в прошлый раз наугад расставим направления токов во всех ветвях и подпишем где какой ток. Видно, что всего у нас 6 ветвей и, соответственно, 6 разных токов (I1…I6).
Теперь запишем второй закон Кирхгофа для всех трех независимых контуров.
Второй закон Кирхгофа для контура I:

Второй закон Кирхгофа для контура II:

Второй закон Кирхгофа для контура III:

У нас есть три уравнения, однако неизвестных токов аж 6. Как и в прошлой задаче для получения недостающих уравнений запишем первые законы Кирхгофа для узлов.
Первый закон Кирхгофа для узла А:

Первый закон Кирхгофа для узла В:

Первый закон Кирхгофа для узла С:

Собственно, у нас теперь есть система из 6 уравнений с 6 неизвестными. Остается только решить эту систему

Подставляя числа, заданные в условии, получаем

Опуская решения за пределами статьи, приведем итоговый результат

Господа, мы видим, что почти все токи, кроме I4 получились у нас со знаками «минус». Это значит, что мы не угадали их направление, когда рисовали стрелочки на рисунке 2 . То есть все токи, кроме тока I4 на самом деле текут в противоположные стороны. А ток I4 течет так, как мы нарисовали. Хотя бы с ним мы угадали верно.
Теперь все по тому же закону Ома ровно как в прошлом примере рассчитаем напряжения на резисторах:

Вот и все, господа: схема рассчитана, а задачка решена. Таким образом, вы теперь обладаете весьма мощным инструментом по расчету электрических схем. С помощью двух законов Кирхгофа и закона Ома вы сможете рассчитать весьма непростые схемы, найти величины токов и их направления, а также напряжения на всех нагрузках цепи. Более того, зная токи и напряжения вы легко сможете рассчитать и мощности, которые на этих резисторах выделяются, если воспользуетесь рекомендациями из моей предыдущей статьи .
На этом на сегодня все господа. Огромной вам всем удачи и успешных расчетов!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Практическое применение законов Кирхгофа
В мире электротехники законы Кирхгофа остаются одними из самых фундаментальных и важных законов. Они были разработаны немецким физиком Густавом Кирхгофом в середине 19 века и по сей день являются неотъемлемой частью инженерных расчетов и проектирования различных электрических цепей.
Первый и второй законы Кирхгофа определяют основные принципы электрических цепей и объясняют, как электрический ток распределяется в сложных цепях с несколькими элементами. Они также позволяют рассчитывать напряжения и токи в различных участках электрической цепи, что позволяет инженерам проектировать и строить эффективные и безопасные электрические установки и системы электроснабжения .
В этой статье мы рассмотрим основные законы Кирхгофа и их применение в решении различных задач в электрических цепях. Мы также рассмотрим практическое применение законов Кирхгофа в современной электротехнике .

Примеры применения первого закона Кирхгофа в электрических цепях
Первый закон Кирхгофа, также известный как закон о сохранении заряда, утверждает, что в любой точке электрической цепи сумма токов, втекающих и вытекающих из этой точки, равна нулю. Иными словами, любое количество тока, втекающего в точку, должно быть компенсировано таким же количеством тока, вытекающего из этой точки.
Этот закон основан на том, что заряд, не может исчезнуть или появиться из ниоткуда. Всякий раз, когда электрический ток движется по проводнику, он несет определенный заряд, и этот заряд должен сохраняться в пределах замкнутой электрической цепи.
Рассмотрим пример применения первого закона Кирхгофа. Предположим, что у нас есть электрическая цепь, состоящая из двух ламп, подключенных к источнику питания.
Если мы выберем любую точку в этой цепи, например, точку между двумя лампами, то согласно первому закону Кирхгофа, сумма токов, втекающих и вытекающих из этой точки, должна быть равна нулю. Это означает, что ток, втекающий в эту точку, должен быть равен току, вытекающему из нее.
Первый закон Кирхгофа является фундаментальным принципом электрических цепей и используется при решении множества задач в электротехнике. Он также является основой для второго закона Кирхгофа, который мы рассмотрим далее.
Примеры применения второго закона Кирхгофа в электрических цепях
Второй закон Кирхгофа, также известный как закон о петлях, утверждает, что алгебраическая сумма произведений сопротивлений и токов в каждой замкнутой петле электрической цепи должна быть равна электродвижущей силе, действующей в этой петле.
Этот закон основан на законе Ома, который гласит, что напряжение между двумя точками в электрической цепи равно произведению силы тока на сопротивление между этими точками.
Если применить закон Ома к каждому элементу электрической цепи, то можно определить напряжение на каждом элементе. Затем, используя второй закон Кирхгофа, можно определить ток в каждой петле цепи.
Рассмотрим пример применения второго закона Кирхгофа. Предположим, что у нас есть электрическая цепь, состоящая из трех сопротивлений и источника питания.
Если мы выберем замкнутую петлю, которая включает два сопротивления и источник питания, то согласно второму закону Кирхгофа, сумма произведений сопротивлений и токов в этой петле должна быть равна электродвижущей силе, действующей в этой петле.
Второй закон Кирхгофа позволяет электрикам рассчитывать токи и напряжения в сложных электрических цепях, содержащих множество элементов.
Общий алгоритм решения задач с применением законов Кирхгофа
Алгоритм решения задач с применением законов Кирхгофа включает следующие шаги:
- Нарисуйте электрическую схему и обозначьте направление тока в каждой ветви.
- Напишите уравнения для всех узлов схемы с использованием первого закона Кирхгофа (закона сохранения заряда).
- Напишите уравнения для всех замкнутых контуров схемы с использованием второго закона Кирхгофа (закона сохранения энергии).
- Решите систему уравнений для всех узлов и контуров, чтобы найти значения неизвестных токов и напряжений.
- Проверьте свои результаты, просуммировав все токи в каждом узле и убедившись, что они совпадают.
Применение законов Кирхгофа может показаться сложным на первый взгляд, но с практикой и опытом вы сможете быстро решать электрические задачи, используя эти законы.
Применение законов Кирхгофа:
Значение законов Кирхгофа в современной электротехнике
Законы Кирхгофа имеют широкое практическое применение в электротехнике. Рассмотрим несколько примеров.
Первым примером может быть расчет электрической сети в доме. При этом мы можем использовать законы Кирхгофа для определения токов и напряжений в различных участках сети. Таким образом, мы сможем определить оптимальное расположение и параметры проводов, чтобы обеспечить эффективное и безопасное функционирование электрической сети.
Вторым примером может быть проектирование и расчет электрических цепей в промышленных установках. Законы Кирхгофа позволяют определить параметры цепи, необходимые для ее оптимальной работы, и обеспечить эффективное использование электроэнергии.
Третьим примером может быть применение законов Кирхгофа при проектировании и разработке электронных схем. Законы Кирхгофа позволяют определить токи и напряжения в различных участках схемы, а также оптимизировать ее параметры для достижения максимальной эффективности.
В современной электротехнике практическое применение законов Кирхгофа невозможно переоценить. Они являются основным инструментом для расчета и анализа электрических цепей и схем, а также используются для оптимизации производственных процессов и снижения затрат на электроэнергию.
Кроме законов Кирхгофа, в электротехнике есть и другие законы, которые имеют большую важность. Некоторые из них:
- Закон Ома: устанавливает связь между напряжением, током и сопротивлением в электрической цепи.
- Закон Фарадея: описывает процесс электромагнитной индукции и связь между магнитным полем и электрическим током.
- Закон Ампера: связывает магнитное поле с электрическим током, т.е. говорит о том, как магнитное поле влияет на ток в проводнике.
- Закон Джоуля-Ленца: определяет количество тепла, которое выделяется в проводнике при прохождении через него электрического тока.
- Закон Кулона: определяет силу взаимодействия между двумя электрическими зарядами.
Все эти законы необходимы для понимания различных процессов, происходящих в электрических цепях и устройствах, и широко применяются в различных областях электротехники.
Телеграмм канал для тех, кто каждый день хочет узнавать новое и интересное: Школа для электрика
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Не пропустите обновления, подпишитесь на наши соцсети:
Второй закон Кирхгофа и его определение
В едином замкнутом контуре алгебраическая сумма ЭДС будет равняться на значение, которое суммирует изменения напряжения на всеобщее количество резистивных элементов данного контура.
Второе правило Кирхгофа актуально в сетях с постоянным и/или переменным током. В формулировке закона используется именно понятие алгебраическая сумма, так как она может быть указана со знаком плюс или минус. Точное определение возможно в таком случае только посредством простого, но эффективного алгоритма. Для начала надо подобрать какое-то направление для обхода контура, по/против часовой стрелке, на собственное усмотрение. Само направление тока подбирается только через элементы цепи. После следует определить знаки «+» и «-» для напряжениях и ЭДС. Напряжения нужно записывать с отрицательным знаком, когда ток не соответствует обходу контура в плане направления и с плюсом в случае совпадения. То же самое правило нужно использовать и в том случае, когда необходимо отметить ЭДС.
Второй закон Кирхгофа — практическое применение
На практике второй закон Кирхгофа применяется успешно для расчета электрических цепей. Благодаря его разъяснению можно рассчитать необходимые параметры в сложных электрических цепях. Когда присутствует необходимость рассчитать значение тока и/или направление всегда выручит второй закон Кирхгофа. Невзирая на то, что правила Кирхгофа были сформулированы в далеком 1845 году, они показали себя как рабочие и не вызывают вопросы ни у кого. Теория электрических цепей была бы неполной без наличия этих законов, которые так хорошо подходят для решения различных уравнений в этой области.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:




