Если в десятичной системе счисления числа записываются с помощью десяти различных символов (от 0 до 9), то в двоичной системе — с помощью всего двух символов: 0 и 1. Такая система необходима для всех устройств, в которых информация представлена в виде последовательностей двух возможных состояний носителя, а это практически вся современная вычислительная техника.
Так же, как в десятичной системе разряды являются степенями основания 10, в двоичной системе разряды являются степенями основания 2:
| 10 000 000 000 | 1 000 000 000 | 100 000 000 | 10 000 000 | 1 000 000 | 100 000 | 10 000 | 1000 | 100 | 10 | 1 |
| 10 10 | 10 9 | 10 8 | 10 7 | 10 6 | 10 5 | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 2 10 | 2 9 | 2 8 | 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
При этом значением числа будет сумма значений всех разрядов. Например, переведем в привычный десятичный вид двоичное число 110001:
1 * 2 5 + 1 * 2 4 + 0 * 2 3 + 0 * 2 2 + 0 * 2 1 + 1 * 2 0 = 49
Или то же самое чуть иначе:
1 * 32 + 1 * 16 + 0 * 8 + 0 * 4 + 0 * 2 + 1 * 1 = 49
Биты и байты
В современных вычислительных системах информация представлена не в виде непрерывного потока двоичных символов (условных нолей и единиц), а за единицу информации, как правило, принимается байт (byte).
Байт состоит из восьми битов (т.е. это восьмиразрядное двоичное число), соответственно, он имеет 256 (2 8 ) возможных значений.
Именно поэтому стандартные варианты разрядности кратны восьми. Например, для операционных систем это 32 или 64 разряда (или бита), а для цифрового звука: 8, 16, 24 и 32.
Важно не запутаться в трех основных значениях, которые определяются разрядностью числа: количество возможных значений, максимальное значение и значение старшего бита/разряда.
Например, для 8-разрядного числа количество возможных значений = 256 (0 — 255), максимальное значение = 255, а значение старшего бита = 128.
Понятия и определения
Перед началом изучения бинарной формы записи значений необходимо запомнить несколько определений:
- число – это количество, цифра – символ, используемый для его обозначения;
- основание системы счисления (СС) – количество цифр в СС;
- разряд – индекс цифры, который начинается с нуля и отсчитывается в направлении «справа-налево»;
- бит – простейшая информационная единица в информатике, представленная 0 и 1.
Подробнее необходимо остановиться на понятии системы счисления. Так называется набор цифр и согласованных правил описания имеющихся чисел.
Применение двоичной системы счисления в реальной жизни
Система счисления – это…
Система счисления (или numeral system) – это некоторый символический метод записи чисел, представление чисел через письменные знаки.
- дает представление множества чисел – целых или вещественных;
- используется для отображения алгебраической и арифметической структуры чисел;
- позволяет каждое число представить в уникальной форме.
Существуют разные системы счисления: позиционные, непозиционные и смешанные.
Позиционный тип
Значение числа будет определяться в такой системе не только цифрами, но и их позицией. Это арабская система (десятичная), где первый разряд справа отводится под единицы, второй – для десятков, третий – для сотен и так далее.
В позиционной системе число 468 будет записываться как:
- 8 единиц;
- 6 десятков;
- 4 сотни.
К данной категории относят системы счисления с основаниями 16, 8 и 2.
Непозиционный тип
Значение чисел определяется знаком (цифрой). Чтобы обозначить единицы, десятки, сотни, тысячи в непозиционных системах используются специальные символы. Положение цифры в числе не будет иметь значения. Система способна накладывать некоторые ограничения на положение цифровых элементов. Пример – расположение в порядке убывания.
В качестве наиболее распространенного варианта непозиционных систем счисления выступают римские цифры. Число 475 здесь может иметь несколько способов записи:
- CCCCXXXXXXXIIIII;
- CDLXXV.
Второй вариант записи использует вычитание и прибавление. Значение цифры, которая стоит справа от большего числа, отнимается от этого самого числа. Если цифра стоит справа, значение должно прибавляться.
Двоичная система
Двоичная система счисления – позиционная система счисления с основанием 2. Также называется бинарной (binary). Она широко используется в вычислительной технике и других современных устройствах.
Двоичные системы счисления используют всего две цифры при записи информации – 0 и 1. Они появились еще в Древнем Китае, но современная binary system стала развиваться в 17 веке, а ее применение началось в середине 20-го века.
История развития
Томас Хэрриот, астроном и математик из Англии, в 1605 году впервые описал двоичное представление чисел, а Фрэнсис Бэкон, философ, создал шифр из двух символов – A и B.
В 1670-м году Хуан Карамюэль-и-Лобковиц, богослуживец из Испании, опубликовал разные способы представления чисел в системах счисления. В публикации было упомянуто и про двоичную интерпретацию.
Наиболее значительными в развитии binary system стали работы Готфрида Лейбница, математика из Германии. В 1703 году он описал двоичную арифметику – возможные математические операции с двоичными числами.
В 1838 году изобретатель из Америки Самюэл Морзе создал одноименный шифр, который включал в себя всего два символа – точку и тире. Они передавались по телеграфу в виде сигналов различной длины. Азбука Морзе – это не бинарная система в строгом понимании термина, но двоичный принцип в ней использовался. Именно с ней соответствующий вариант представления записей продемонстрировал свою значимость.
Чуть позже, в 1847 году, Джордж Буль, математик из Англии, создал «булеву алгебру». В ней появились такие понятия как «ложь» и «истина», а также определенные логические законы.
В 1937 году Клод Шеннон, инженер из Америки, объединил двоичный принцип, булеву логику и электрические схемы. Он же ввел понятие «бит» – минимального количества информации, где:
- 0 – это отсутствие тока, «ложь» (0 бит);
- 1 – наличие тока, «истина» (1 бит).
С того самого момента бинарная система счисления стала активно применяться в вычислительной технике, включая современные компьютеры.
Числа в binary system
Двоичным числом называется число, которое состоит из двоичных цифр. Их всего две – 0 и 1. В качестве записей в binary system могут использовать разные значения: «ток есть» и «тока нет», «истина» и «ложь» и так далее.
Ниже можно увидеть числа в двоичной системе, а также их интерпретации в других системах счисления:
Эта таблица поможет лучше ориентироваться в расчетах и быстрее разобраться со способами представления чисел.
Любое натуральное число может быть закодировано в бинарном представлении. Оно будет представлять собой некоторую последовательность единиц и нулей.
Особенности
У двоичной системы счисления имеются как преимущества, так и недостатки. К ее слабым сторонам относят то, что она не понятна человеку на уровне интуиции. Также сюда можно отнести следующие моменты:
- Неудобство работы с большими числами. Это вызвано длинной записью значения. Пример – RGB: 25510, 25510, 25510. Здесь и далее нижний индекс будет указывать на основание системы. Значения RGB обычно записываются в шестнадцатеричной форме представления: FF16, FF16, FF16. При переводе записи в бинарный вид получится 1111112, 1111112, 1111112. Такая форма записи выглядит громоздко и непонятно.
- Отсутствие реального применения в жизни (за исключением компьютеров и иной вычислительной техники).
- Долгое вычисление вручную.
Двоичная система счисления для вычислительной техники – это некий стандарт. Из него следуют преимущества рассматриваемой формы представления информации:
- позиционная система предусматривает разряды;
- можно осуществлять различные арифметические действия;
- допустимо построение логики;
- подходит для шифрования данных;
- используется в качестве «родного» для компьютеров и других устройств.
Binary System – стандарт, используемый в ЭВМ. Он удобен при расчетах и занимает намного меньше пространства, чем остальные формы представления числовых записей.
Перевод чисел из десятичной системы счисления в двоичную
Перевод целой части десятичного числа производится путем поочередного деления частного на основание двоичной системы, то есть на два. В остатке от деления останется либо ноль, либо единица. Эти остатки записываются, начиная с последнего частного в направлении слева направо. Это и будет двоичным представлением десятичного числа.
Для перевода десятичного числа 29 в двоичный формат:
Делят 29 на два, получают 14 и в остатке 1. Остаток следует запомнить.
Затем частное от деления, то есть число 14 снова делят на два, получено 7 и в остатке 0 (ноль).
Разделим 7 на два, получим частное 3 и остаток 1.
Три делят на два, получено в частном 1 и остаток 1.
Так как последнее частное 1 меньше основания системы счисления, то есть числа 2, то последовательное деление прекращают.
Затем записывают остатки, начиная с последнего частного, и получают последовательность чисел: 11101. Таким образом, десятичное число 29 в двоичной системе счисления равно 11101.
Еще один пример: перевод числа 37 в двоичный формат.
Получен результат: 100101.
Если десятичные числа расположить последовательно и сопоставить с их двоичными эквивалентами, то можно увидеть некоторую закономерность.
Таблица двоичной системы счисления
Как видно из таблицы, после 11 в числовом ряду двоичных чисел идет число 100. Так как в двоичной системе счисления только два знака 0 и 1 для обозначения числа, то происходит сдвиг разрядной сетки влево. После двузначного числа 11 идет трехзначное число 100.
Таблицей двоичной системы удобно пользоваться для перевода только небольших десятичных чисел. Ее даже рекомендуется запомнить, как таблицу умножения в математике. Но ни в коем случае нельзя по таблице переводить отдельные цифры числа в десятичный формат. Это приведет к ошибке. Например, десятичное число 15 это не 1 и 101, (вместе 1101), а все-таки 1111.
Перевод двоичных чисел в десятичную систему счисления
Обратный перевод двоичного числа в десятичную систему производится также строго по правилу перевода.
Сначала нумеруются разряды двоичного числа справа налево, начиная с нулевого, а затем каждая цифра двоичного числа умножается на основание двоичной системы, то есть на два, возведенной в степень соответствующего разряда. Полученные произведения суммируются, и получается десятичное число.
Например: двоичное число 1110001 в десятичной системе равно 113.
Нумеруем разряды числа, начиная с нуля: 1(6) 1(5) 1(4) 0(3) 0(2) 0(1) 1(0).
Каждую цифру двоичного числа умножаем на два в степени разряда и суммируем:
1*2 6 + 1*2 5 + 1*2 4 +0*2 3 + 0*2 2 + 0*2 1 + 1*2 0 = 64 + 32 + 16 + 0 + 0 + 0 +1 = 113
Следует помнить, что любое число в степени ноль равно единице.
Двоичная система счисления была описана Готфридом Вильгельмом Лейбницем в 18 веке. На это его вдохновили гексограммы из китайской книги Перемен, которые соответствовали двоичным числам от 0 до 111111.
Двоичная система счисления
| Двоичная система счисления – это система счисления по основанию 2.
Алфавит системы счисления: 0, 1.
Перевод десятичного числа в двоичную систему счисления методом подбора степеней числа 2
Для перевода двоичных чисел в десятичную систему счисления, используют метод подбора степеней двойки.
Пусть дано десятичное число 2110.
1) Подберём ближайшую наименьшую степень числа 2 к данному числу: 2 4 = 16;
2) Вычтем найденное число из данного: 21 — 16 = 5;
3) Повторить, пока не достигнем нуля.
В результате, мы получим следующие степени:
Найденные нами степени – это позиции цифры 1 в двоичном числе, а отсутствующие степени – это нули:
Перевод целого десятичного числа в другую систему счисления методом деления на новое основание
✒ Определение: Для перевода целого десятичного числа в другую систему счисления, необходимо делить данное число на новое основание (той системы счисления, в которую необходимо осуществить перевод). Ответ складывается из остатков от деления.
Переведите число 1310 в двоичную систему счисления.
Арифметические операции в двоичной системе счисления
Все вычисления в компьютере выполняются в двоичной системе счисления.
Рассмотрим базовые арифметические операции.
Общепринятые системы счисления
Человечество в ходе своего развития со временем стало нуждаться в способах подсчета. Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.
В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.
С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.
Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления. Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.
Узнай, какие ИТ — профессии
входят в ТОП-30 с доходом
от 210 000 ₽/мес
Павел Симонов
Исполнительный директор Geekbrains
Команда GeekBrains совместно с международными специалистами по развитию карьеры подготовили материалы, которые помогут вам начать путь к профессии мечты.
Подборка содержит только самые востребованные и высокооплачиваемые специальности и направления в IT-сфере. 86% наших учеников с помощью данных материалов определились с карьерной целью на ближайшее будущее!
Скачивайте и используйте уже сегодня:
Павел Симонов
Исполнительный директор Geekbrains
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ бесплатных нейросетей для упрощения работы и увеличения заработка
Только проверенные нейросети с доступом из России и свободным использованием
ТОП-100 площадок для поиска работы от GeekBrains
Список проверенных ресурсов реальных вакансий с доходом от 210 000 ₽
Получить подборку бесплатно
Уже скачали 26166
Любая система счисления принадлежит к одной из двух категорий:
Позиционные СС
Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).
Непозиционные СС
Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.
Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.
Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.
Когда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.
Числа, используемые в двоичной системе счисления
Состав двоичной системы счисления — цифры 0 и 1. Основание равно 2. В крайней правой позиции числа указывается количество единиц, левее — количество двоек, затем количество четверок и т. д.
Таким образом, любое натуральное число кодируется в последовательный ряд из нулей и единиц — это и будет являться двоичной системой счисления. Решение такой задачи покажем на примере ниже.
10112 = 1*23 + 0*2*2+1*21+1*20 =1*8 + 1*2+1=1110
Как известно, двоичная система счисления используется вычислительной техникой для хранения информации, а также для преобразования данных в графические изображения. В свою очередь обработка двоичного кода требует предварительного размещения каждой цифры внутри особой электронной схемы (триггера). Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».
Отдельное число, состоящее из нескольких цифр, сохраняется группой триггеров — регистром. Оперативная память компьютера фактически является совокупностью таких регистров.
Перевод чисел из одной системы счисления в другую
Я не буду вам рассказывать как можно с помощью ручки и бумаги перевести любое число из одной системы счисления в другую. Об этом вы можете (при желании) почитать в популярной литературе по микроконтроллерам.
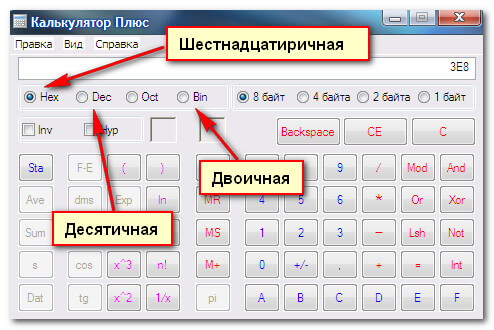
Самый простой способ перевода чисел из одной системы счисления в другую — калькулятор, который имеет так называемый «инженерный режим». Если у вас нет такого калькулятора, то всегда можно воспользоваться стандартным калькулятором «Windows» , переведя его в «инженерный режим» :
(17 голосов, оценка: 4,71 из 5)
Двоичная и шестнадцатиричная система счисления, арифметические операции в двоичной системе
Системы счисления: двоичная, шестнадцатиричная и их применение в микроконтроллерах, арифметические операции в двоичной системе
Перевод из десятичной системы в любую другую. Перевод целых чисел
Целое десятичное число нужно поделить на основание новой системы счисления. Остаток от этого деления является самым младшим разрядом в новой записи числа. Результат деления вновь делится на основание. Остаток от этого деления будет следующим разрядом в новой записи числа, результат деления вновь делится на основание и т.д. до тех пор, пока в результате деления получится число, меньшее по величине, чем основание новой системы. Остаток этого последнего деления будет предпоследним разрядом в новой записи числа, а результат этого последнего деления — самым старшим разрядом в новой записи числа.
Проверка перевода осуществляется по формуле (11.2), так, как это показано ниже на примерах.
Пример. Перевести десятичное число 125 в двоичную, восьмеричную и шестнадцатеричную системы счисления. Проверить результаты по формуле (П11.2).
;
;
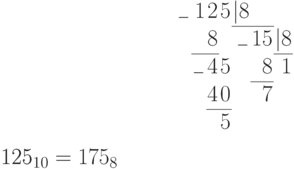
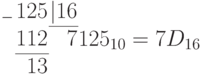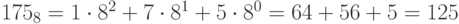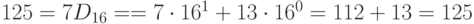.В рассмотренном примере при переводе вместо коэффициента 
используется его десятичный эквивалент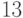 
в соответствии с таблицей 11.2.
Перевод из двоичной системы в шестнадцатеричную (восьмеричную)
Как уже было сказано выше, шестнадцатеричный и восьмеричный коды используются для более компактной и удобной записи двоичных чисел. Так, программирование в машинных кодах осуществляется в большинстве случаев в шестнадцатеричном коде. Правила перевода для шестнадцатеричной и восьмеричной системы структурно одинаковы, отличия для восьмеричной системы отображаются в скобках.
Двоичная запись числа делится на группы по четыре ( три ) двоичных знака влево и вправо от запятой, отделяющей целые и дробные части Неполные крайние группы (если они есть) дополняются нулями до четырех ( трех ) знаков. Каждая группа заменяется одним шестнадцатеричным ( восьмеричным ) знаком в соответствии с кодом группы (табл. 11.2).
| 0000 | 0 | 0 | 000 | 0 |
| 0001 | 1 | 1 | 001 | 1 |
| 0010 | 2 | 2 | 010 | 2 |
| 0011 | 3 | 3 | 011 | 3 |
| 0100 | 4 | 4 | 100 | 4 |
| 0101 | 5 | 5 | 101 | 5 |
| 0110 | 6 | 6 | 110 | 6 |
| 0111 | 7 | 7 | 111 | 7 |
| 1000 | 8 | 8 | ||
| 1001 | 9 | 9 | ||
| 1010 | A | 10 | ||
| 1011 | B | 11 | ||
| 1100 | C | 12 | ||
| 1101 | D | 13 | ||
| 1110 | E | 14 | ||
| 1111 | F | 15 |
- перевод в шестнадцатеричную систему:
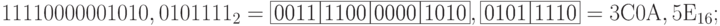
Перевод из шестнадцатеричной (восьмеричной) системы в двоичную
Обычно программы в машинных кодах записаны в шестнадцатеричной системе счисления, реже — в восьмеричной. При необходимости отдельные числа такой программы записываются в двоичном коде, например, при рассмотрении форматов регистров, кодов операции команд и т.п. В этом случае нужен обратный перевод из шестнадцатеричной ( восьмеричной) системы счисления в двоичную по следующему правилу.
Каждая цифра (без всяких сокращений!) шестнадцатеричного ( восьмеричного ) числа заменяется одной двоичной группой из четырех ( трех ) двоичных знаков (табл. 11.2).
- для шестнадцатеричного числа:
; - для восьмеричного числа:
.
Как показано в примерах, крайние нули слева и справа при желании можно не писать, но такое сокращение делается уже после перевода в двоичную систему.
