Этот метод применяется в тех случаях, когда нужно рассчитать ток только в одной ветви аЬ сложной электрической цепи, например в приемнике, подключенном к выходу усилителя. Подобного рода задача часто встречается также при расчетах устройств для электрических измерений неэлектрических величин, систем автоматического регулирования и т.п.
Будем считать ветвь аЬ внешней по отношению ко всей остальной части электрической цепи (рис. 1.16а), которая может содержать источники ЭДС, источники тока и постоянные сопротивления. Эту часть цепи рассматриваем как активный двухполюсник по отношению к ветви аЬ, с которой она соединяется двумя полюсами а и Ь. На этом рисунке активный двухполюсник условно изображен в виде прямоугольника с буквой А (активный) и показаны два его вывода а и Ь .
Если к выводам а и Ь активного двухполюсника подключить сопротивление Кн (нагрузить), то во внешней части цепи (ветви аЬ) появится ток 1аЬ = / (рис. 1.16а).
Рис. 1.16. Иллюстрация метода эквивалентного генератора (пояснения в тексте)
Рассматриваемый метод позволяет рассчитать ток в сопротивлении Ян (сопротивлении нагрузки), представляя активный двухполюсник в виде эквивалентного генератора (отсюда название метода).
Чтобы определить параметры эквивалентного генератора, произведем в заданной электрической цепи (рис. 1.16а) ряд последовательных преобразований.
Включим последовательно с приемником и навстречу друг другу два одинаковых источника ЭДС Ех = Ег (рис. 1.166). Так как эти ЭДС одинаковые и действуют в противоположных направлениях, то ток 1аЬ = / в ветви аЬ не изменится. Следовательно, не изменится и режим работы активного двухполюсника, т.е. схема рис. 1.166 эквивалентна заданной (рис. 1.16а).
Для расчета тока 1аЬ= I в цепи (рис. 1.166) применим метод наложения (см. разд. 1.9.3), представив ток I в виде суммы трех частичных токов: тока 1 А при действии всех источников активного двухполюсника А; I 1 при действии источника ЭДС ?, и тока I» при действии источника ЭДС Е2:
Выберем ЭДС ?, = Е2 равные напряжению холостого хо- да 11аЬх = их активного двухполюсника между выводами а и Ь , т.е. напряжению при отключенном приемнике (/ = 0 ), как показано на рис. 1.16в. В этом случае при действии всех источников активного двухполюсника и источника ЭДС Ех = их ток в сопротивлении нагрузки (рис. 1.16г) будет равен нулю (1 А +1 1 = 0).
Следовательно, при определении тока / все эти источники можно исключить, заменив их резистивными элементами с сопротивлениями, равными внутренним сопротивлениям соответствующих источников. В полученной после такого преобразования электрической цепи (рис. 1.16д) активный двухполюсник заменен пассивным, который содержит только резистивные элементы, так как источники активного двухполюсника не действуют. Параметром пассивного двухполюсника является его входное сопротивление Кдх между выводами а и Ь . Ток / в приемнике при действии одной ЭДС Е2 = их (рис. 1.16д) такой же, как и для заданной цепи (рис. 1.16а).
Электротехника (ТОЭ). Лекция 9. Метод эквивалентного генератора | Решение задач
Сравнив схемы на рис. 1.16а и 1.16д, заключаем, что для активного двухполюсника можно составить эквивалентную схему замещения с ЭДС Еэк = Е2 =11х и внутренним сопротивлением Яэк = Квх, т.е. заменить его эквивалентным генератором (рис. 1.16е).
Для электрической цепи с эквивалентным генератором (рис. 1.16е)
Выражение (1.17) показывает, что для определения тока в приемнике достаточно знать два параметра активного двухполюсника: напряжение холостого хода между его выводами и входное сопротивление, которые можно измерить при помощи соответствующих приборов или рассчитать. Параметры электрической цепи активного двухполюсника при этом могут быть неизвестны.
Для определения параметров активного двухполюсника часто используются экспериментальные методы холостого хода и короткого замыкания. Измерив при помощи вольтметра напряжение холостого хода между выводами двухполюсника их, а затем при короткозамкнутых выводах а и Ь (Ян = 0 ) — ток короткого замыкания при помощи амперметра, непосредственно из уравнения (1.17) можно определить входное сопротивление
В качестве примера рассчитаем ток /5 в ветви с резистором Я5 (рис. 1.17а), методом эквивалентного активного двухполюсника. Параметры схемы Е, Ях — Я5 известны.
Рис. 1.17. Иллюстрация метода эквивалентного генератора (пояснения в тексте)
В соответствии с методом эквивалентного генератора представляем исходную цепь в виде эквивалентного генератора с параметрами — и ветви с сопротивлением (рис. 1.176).
Определяем напряжение иаЬх при разомкнутой ветви аЬ с резистором Я5 (рис. 1.17в):
Сопротивление Я.зкаЬ определяем по схеме рис. 1.17г (внутреннее сопротивление источника ЭДС равно нулю):
Ток /5 в диагональной ветви моста находим из схемы рис. 1.176:
Метод эквивалентного генератора
Метод эквивалентного генератора применяется для определения тока одной из ветвей электрической цепи в том случае, когда расчет всей схемы не требуется. В основу метода положена теорема об активном двухполюснике (теорема Гельмгольца-Тевенена). Основная идея метода заключается в том, что часть цепи, параметры которой определять нет необходимости, заменяется эквивалентным генератором с известной эдс и сопротивлением. Метод часто применяется для расчета режима электрической цепи.
Алгоритм состоит из следующих шагов:
- Выбранная для расчета ветвь удаляется из схемы, а места образовавшегося разрыва обозначаются буквами. Оставшаяся часть схемы будет представлять собой эквивалентный генератор.
- Рассчитывается эквивалентная эдс генератора.
- Определяется эквивалентное сопротивление генератора.
- По найденным в пунктах 2 и 3 параметрам генератора определяется ток через исключенную в пункте 1 ветвь.
Метод эквивалентного генератора: примеры решения
Рассмотрим пример расчета электрической схемы методом эквивалентного генератора (рисунок 1).
Допустим, что необходимо рассчитать ток Iab через резистор R4. Тогда преобразования схема будет иметь вид, представленный на рисунке 2.
После преобразования ток через резистор Rab (R4) определяется по формуле
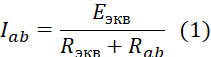
Для того, чтобы рассчитать значения Еэкв и Rэкв необходимо рассмотреть режим холостого хода генератора. Для этого необходимо обеспечить его работу без нагрузки, то есть условно отсоединить от цепи исследуемую ветвь ab (рисунок 3).
Для представленной схемы напряжение Еэкв будет равно
Далее требуется определить эквивалентное сопротивление. Для этого воспользуемся методом пассивного двухполюсника. В этом случае необходимо исключить из схемы источник эдс и найти общее сопротивление цепи (рисунок 4).
Эквивалентное сопротивление полученной схемы определяется по формуле
Теперь можно определить ток, проходящий через резистор ab согласно выражению (1).
Поставленная задача решена.
4.8. Метод эквивалентного генератора
Этот метод дает возможность вычислить ток только одной ветви схемы. Его можно использовать и при необходимости заменить часть схемы эквивалентной ей ветвью. Суть расчета заключается в замене сложной разветвленной схемы эквивалентной ей одноконтурной с подлежащим определению током.
| a I n | Прежде всего схему разбивают на две части: | ||||
| резистор сопротивлением R n (ток в котором I n | |||||
| A | нужно вычислить) и всю остальную часть схемы, | ||||
| R n которая будет питать этот резистор. Эта часть схе- | |||||
| мы | является | активным | двухполюсником | ||
| b | ( рис. 2.22 ). | ||||
| Любой активный двухполюсник можно заме- | |||||
| Рис. 2.22 | |||||
| нить | эквивалентным ему генератором ( рис. 2.23 ). | ||||
ЭДС генератора равна напряжению между зажимами а и b активного двухполюсника в режиме холостого хода. Внутреннее сопротивление генератора равно эквивалентному сопротивлению пассивного двухполюсника относительно входных зажимов. Пассивный двухполюсник получают из активного, закорачи-
| Теоретические основы электротехники. Учеб. пособие | -36- |
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА 2.4. Методы расчета токов
вая идеальные источники ЭДС и разрывая ные источники тока. Таким образом, исходную схему произвольной конфигурации можно заменить одноконтурной, а расчетный ток вычислить по следующей формуле:
| I n = | E г | = | U хх | . |
| R г + R n | ||||
| R г + R n | ||||
a E г 
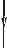I n R n R г 
b Рис. 2.23
Пример . 2.3. Вычислим ток I 4 в схеме, представленной на рис. 2.24 .
| E 3 | R 3 |
| E 1 | R 2 |
| R 5 | E 6 |
| R 1 | |
| E 2 | R 4 |
| a I 4 | b |
| Рис. 2.24 | |
Решение 1. Разделим схему на две части: резистор сопротивлением R 4 и актив- ный двухполюсник, который заменим эквивалентным ему генератором. Для этого нужно определить E г = U хх и R г . 2. Нарисуем схему активного двухполюсника в режиме холостого хода ( рис. 2.25 ). В схеме два тока I 1х и I 2х , замыкающихся по контурам.
| I 1x | E 3 | R 3 | I 2x |
| E 1 | R 2 | ||
| R 5 | E 6 | ||
| R 1 | |||
| E 2 | U xx |
a b Рис. 2.25
| Теоретические основы электротехники. Учеб. пособие | -37- |
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА 2.4. Методы расчета токов 3. Запишем выражение для определения напряжения U хх , рассчитав изменение потенциалов между точками b и а : U хх = E 6 − E 3 − E 1 + R 1 I 1х . 4. Найдем ток I 1х из уравнения по второму закону Кирхгофа: R 1 I 1х + R 2 I 1х = E 1 − E 2 . Отсюда
| I 1х | = E 1 | − E 2 . | ||
| R 1 | + R 2 | |||
| R 3 | В схеме пассивного двухполюсника | |||
| (см. рис. 2.26 ) резистор сопротивлением | ||||
| R 5 закорочен. | ||||
| R 1 | R 2 | R 5 | Очевидно, что эквивалентное со- | |
| противление относительно входных за- | ||||
жимов а и b равно:
| a | b | R = R 1 | R 2 + R . | |
| Рис. 2.26 | г | R 1 | 3 | |
| 5. Вычислим ток I 4 по формуле | + R 2 | |||
| I 4 = | E г | = | U хх . | |
| R г + R 4 | R г + R 4 | |||
2.5. Передачаэнергииотактивногодвухполюсника к пассивному
| I | Для | исследования вопроса рассмотрим | ||||
| схему рис. 2.27 , где Е г и R г активного двухпо- | ||||||
| E г | U | люсника (источника энергии) остаются постоян- | ||||
| ными, а сопротивление пассивного двухполюсни- | ||||||
| R г | R н = 0- ∞ ка (нагрузки) меняется от нуля до бесконечности. | |||||
| Выясним, при каком сопротивлении R н на | ||||||
| нагрузке будет выделяться максимальная мощ- | ||||||
| Рис. 2.27 | ность. Составим уравнение баланса мощностей: | |||||
| Е | г | I = P | + R I 2 . | |||
| н | г | |||||
| Теоретические основы электротехники. Учеб. пособие | -38- |
| ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА | |||||||||||||||||||||||||||
| 2.5. Передача энергии от активного двухполюсника к пассивному | |||||||||||||||||||||||||||
| Отсюда P | = Е | г | I − R I 2 . | ||||||||||||||||||||||||
| н | г | ||||||||||||||||||||||||||
| Определим, при каком токе на нагрузке будет выделяться максималь- | |||||||||||||||||||||||||||
| ная мощность. Для этого нужно найти производную Р н | по току и приравнять | ||||||||||||||||||||||||||
| ее нулю: | d P н = E | ||||||||||||||||||||||||||
| г | − 2 R I = 0. | ||||||||||||||||||||||||||
| d I | г | ||||||||||||||||||||||||||
| = E . Но по | |||||||||||||||||||||||||||
| Отсюда следует, | что при максимальной мощности ток I | ||||||||||||||||||||||||||
| 2 R | |||||||||||||||||||||||||||
| E г | г | ||||||||||||||||||||||||||
| закону Ома для полной цепи ток | I | = R | |||||||||||||||||||||||||
| + R . | |||||||||||||||||||||||||||
| г | н | ||||||||||||||||||||||||||
| Сравнение этих формул показывает, что максимальная мощность вы- | |||||||||||||||||||||||||||
| деляется на нагрузке при R н | = R г . Такой режим называют согласованным. | ||||||||||||||||||||||||||
| Коэффициент полезного действия определяют как отношение мощно- | |||||||||||||||||||||||||||
| сти полезной к мощности затраченной, т. е. | |||||||||||||||||||||||||||
| η = | Р | R I 2 | = | R I | = | R Е | г | = | R | . | |||||||||||||||||
| н = | E | н | I | н | Е | н | ) | R | н | ||||||||||||||||||
| Р | г | E | г | г | ( R + R | г | н | + R | г | ||||||||||||||||||
| г | н | ||||||||||||||||||||||||||
| При согласованном режиме η = 0,5 , | поэтому этот режим не применяют | ||||||||||||||||||||||||||
| для передачи электрической энергии. Его применяют для передачи сигналов | |||||||||||||||||||||||||||
| и информации на линиях связи. При увеличении сопротивления нагрузки R н | |||||||||||||||||||||||||||
| КПД увеличивается и стремится к | |||||||||||||||||||||||||||
| единице. Представляется, что в ре- | P г | ||||||||||||||||||||||||||
| жиме холостого хода, когда | R н = ∞ | 1 | |||||||||||||||||||||||||
| и тока нет , понятие КПД не сущест- | |||||||||||||||||||||||||||
| вует , так как мощности генератора | η | ||||||||||||||||||||||||||
| Р г и нагрузки Р н равны нулю. | |||||||||||||||||||||||||||
| Уравнение | внешней | вольт- | E г | U | |||||||||||||||||||||||
| амперной характеристики генерато- | 0,5 | ||||||||||||||||||||||||||
| ра имеет следующий вид: | |||||||||||||||||||||||||||
| U = E г | − R г I . | P н | |||||||||||||||||||||||||
| Графики зависимостей U ( I ) , | I | ||||||||||||||||||||||||||
| Р г ( I ) , Р н ( I ) и η ( I ) приведены на | I кз | I кз | |||||||||||||||||||||||||
| рис. 2.28 . | 2 | ||||||||||||||||||||||||||
| В режиме холостого хода ток | Рис. 2.28 | ||||||||||||||||||||||||||
| равен нулю, в режиме короткого за- | |||||||||||||||||||||||||||
| Е г . | |||||||||||||||||||||||||||
| мыкания ( R | = 0 ) ток имеет максимальное значение I | кз | = | ||||||||||||||||||||||||
| н | R | ||||||||||||||||||||||||||
| г | |||||||||||||||||||||||||||
| | Теоретические основы электротехники. Учеб. пособие | -39- | |||||||||||||||||||||||||
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА 2.5. Передача энергии от активного двухполюсника к пассивному
| При согласованном режиме ток I = | Е г | = | I кз | , мощность нагрузки |
| 2 R | 2 | |||
| г |
Р н = 1 2 Р г , η = 0,5. Эти зависимости полностью характеризуют режим линии передачи электрической энергии небольшой длины, у которой утечкой тока можно пренебречь.
| Теоретические основы электротехники. Учеб. пособие | -40- |
Применение метода эквивалентного генератора для цепей переменного тока
Определение 1
Метод эквивалентного генератора – это метод преобразования электрической цепи, при использовании которого схемы из нескольких ветвей с источниками электродвижущей силы приводятся к одной ветви с эквивалентным значением.
Метод эквивалентного генератора позволяет вычислить ток только в одной ветви, поэтому расчет повторяется несколько раз (столько раз, сколько ветвей содержится в рассматриваемой цепи). По отношению к рассчитываемой ветви двухполюсник заменяется эквивалентным генератором, у которого электродвижущая сила равняется напряжению холостого хода, образующегося на зажимах данной ветви. При этом внутреннее сопротивление равно сопротивлению двухполюсника. Рассмотрим схему на рисунке ниже.
Статья: Применение метода эквивалентного генератора для цепей переменного тока
Найди решение своей задачи среди 1 000 000 ответов
Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ
Если мы будем рассчитывать ветвь –Е1R1, то остальную часть схемы можно заключить в прямоугольник, которая и будет являться эквивалентным генератором. Тогда ток в рассматриваемой цепи можно рассчитать при помощи закона Ома:
$I = (Ег + –Е) / Rг + R$
Замечание 1
Знак в выше представленном выражении зависит от направления электродвижущей силы в рассчитываемой ветви.
Определение 2
Электродвижущая сила – это способность источника тока создавать разность потенциалов.
Начинай год правильно
Выигрывай призы на сумму 400 000 ₽
Алгоритм расчета выглядит следующим образом:
- Сначала из схемы удаляется цепь, которая была выбрана для расчета. Обозначаются узлы, к которым она присоединялась (обычно m и n). Остальная часть схемы цепи будет представлять собой эквивалентный генератор с эквивалентной электродвижущей силой и сопротивлением. Затем эти два параметра рассчитываются.
- Определяется эквивалентное сопротивление генератора. Чтобы это сделать, источник электродвижущей силы закорачивается (заменяется на отрезок провода), а ветви с источниками тока обрываются. После этого рассчитываются входные сопротивления оставшейся части схемы относительно зажимов m и n.
- Для расчета электродвижущей силы генератора выбирается путь от точки m до точки n, так, чтобы он не проходил через ветви с источниками тока, на всем пути отмечаются точки падения напряжения.
- После этого, зная сопротивление генератора и эквивалентную электродвижущую силу, рассчитывается искомый ток.
Применение метода эквивалентного генератора для цепей переменного тока
Рассмотрим схему на рисунке ниже.
Рисунок 2. Схема. Автор24 — интернет-биржа студенческих работ
Допустим, что необходимо определить ток I3, при условии, что нам известны значения сопротивлений и электродвижущих сил рассматриваемой цепи. Для расчета искомого тока обрываем цепь и обозначаем узлы m и n, как показано на рисунке ниже.
Рисунок 3. Схема. Автор24 — интернет-биржа студенческих работ
Оставшаяся часть рассматриваемой схемы является эквивалентным генератором с эквивалентной электродвижущей силой и сопротивлением. Рассчитываем эквивалентное сопротивление генератора. Для этого закорачиваются источники электродвижущей силы закручиваются, а ветви, в состав которых входят источники тока обрываются, как на рисунке ниже.
Рисунок 4. Схема. Автор24 — интернет-биржа студенческих работ
Входное сопротивление относительно зажимов можно рассчитать следующим образом:
$Rг = ((R2 • R3) / (R2 + R3)) + R4+R6$
Для расчета эквивалентной электродвижущей силы генератора, выбирается путь от точки m до точки n, таким образом, чтобы он не проходил ветви, в которых есть источники тока, как показано на рисунке ниже.
Рисунок 5. Схема. Автор24 — интернет-биржа студенческих работ
$Ег = Umn = U2 + U4 + U6 — E2$
Необходимо рассчитать данные напряжения. Так как рассматриваемая схема состоит из двух независимых контуров, то их можно рассчитать по отдельности. Составляются уравнения для второго контура согласно второму закону Кирхгофа:
Из второго контура, где протекает ток источника J определяются следующие напряжения:
Минусы в формулах означают, что направления рассчитываемых напряжений выбраны таким образом, что они противоположны направлениям протекающих токов. Так как нам теперь известны эквивалентная электродвижущая сила и сопротивление генератора, то искомый ток может быть рассчитан по следующей формуле:
Теперь определим ток I4 в этой же схеме. Обрываем цепь и обозначаем напряжение между точками m и n b и получаем:
Рисунок 6. Схема. Автор24 — интернет-биржа студенческих работ
Для определения сопротивления получившегося генератора, обрывается ветвь с источником тока и закорачиваются источники электродвижущей силы, как на рисунке ниже.
Рисунок 7. Схема. Автор24 — интернет-биржа студенческих работ
$Rг = ((R / R3) / (R2 + R3)) + R1$
Выбираем направление пути от точки m к n, аналогичным образом, как для расчета I3 (в обход ветвей с источниками тока). Выбранный путь изображен на рисунке ниже
Рисунок 8. Схема. Автор24 — интернет-биржа студенческих работ
Получается, что эквивалентная электродвижущая сила генератора может быть рассчитана следующим образом:
$Ег = Umn = U1 + U2$
Напряжение U1 равно:
Напряжение U2 можно рассчитать только при условии, что ветвь с источником Е1 подключена параллельно:
Рисунок 9. Схема. Автор24 — интернет-биржа студенческих работ
Получившаяся схема на рисунке ниже позволяет рассчитать напряжение U2
Рисунок 10. Схема. Автор24 — интернет-биржа студенческих работ
$U2 = ((E1 + Eэ) / (R + R3)) • R2$
Получив значение Eг, можно рассчитать искомый ток:
$I4 = (Eг + E2) / (R4 + R6 + Rг)$
Метод эквивалентного генератора
Этот метод основан на сформулированной выше теореме (см. подраздел 1.4) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.
Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.
ЭДС ЕЭ эквивалентного генератора и его внутреннее сопротивление RЭ находятся из режимов холостого хода и короткого замыкания двухполюсника.
Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.
Пример 1.5. В цепи, показанной на рис. 1.20, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).
Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.
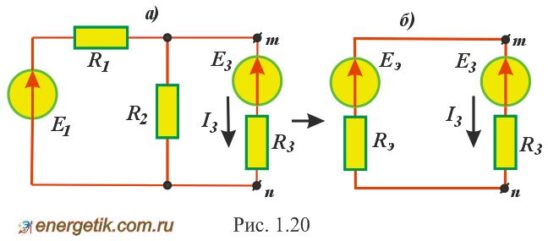
Р е ш е н и е. а) Расчет режима холостого хода.
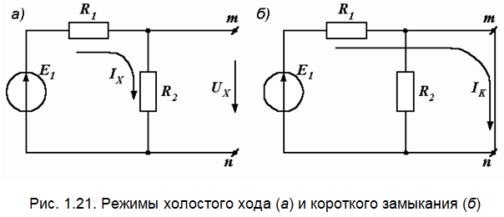
Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:
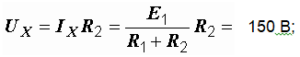
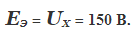
б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания 75 А.
Внутреннее сопротивление эквивалентного генератора:
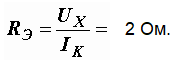
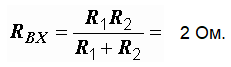
Величину RЭ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно:
Ток в полученной неразветвленной цепи (рис. 1.20, б) определяется по закону Ома:
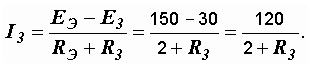
Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 1.22).
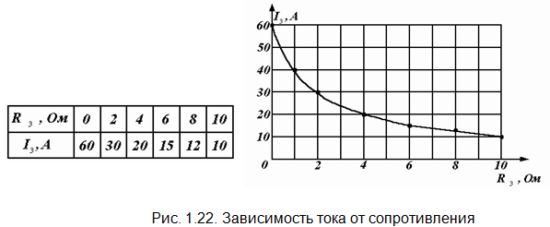
Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя ЕЭ и RЭ, а многократно используем лишь одну простую формулу (1.13).
Электротехника ТОЭ
Лекции и задачи по ТОЭ. На сайте представлен лекционный материал для изучения теоретических основ электротехники и видеоуроки по всем темам. Так же тут можно заказать решение задач, курсовых, расчетных, контрольных и домашних работ. Онлайн помощь на экзамене, контрольной. Решение тестов, занятия по скайпу и др. В ближайшее время на сайт будут добавлены готовые работы на разные темы ТОЭ, ТАУ и другим дисциплинам.
Теория / 3.2. Методы расчета сложных электрических цепей / 3.2.6. Метод эквивалентного генератора
В некоторых случаях при расчете электрической цепи нас интересуют ток, напряжение, мощность только в какой-либо одной ветви схемы. Тогда, чтобы упростить задачу и не рассчитывать всю цепь, применяют метод эквивалентного генератора.
Прежде чем перейти к методу эквивалентного генератора, докажем теорему о компенсации.
Теорема о компенсации. Любой пассивный элемент электрической цепи можно заменить активным элементом, величина ЭДС которого равна падению напряжения на пассивном элементе, а направление противоположно направлению тока в нем.
Докажем эквивалентность такой замены. Рассмотрим для пимера схемы (рис. 3.9, а,б).
Заменим пассивный элемент R 1 источником ЭДС Е1.
Для схемы а запишем уравнение по второму закону Кирхгофа
Отсюда выразим ток в виде
Для схемы б второй закон Кирхгофа запишется в следующей форме:
Ток выразим в виде
При эквивалентной замене ток в сопротивлении R должен остаться неизменным, а он не изменится только в том случае, если E1=R1*I, что и требовалось доказать.
В любой электрической схеме всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от ее структуры, условно изобразить прямоугольником (рис. 3.10).
Например, выделим ветвь с сопротивлением R 5, а всю остальную часть заключим в прямоугольник.
Заключенную в прямоугольник часть схемы, которая двумя выводами подключается к выделенной ветви, называют двухполюсником.
Чаще всего нас не интересует часть схемы, заключенная в двухполюснике, и его обозначают прямоугольником с двумя выводами, к которым присоединяется интересующая нас ветвь (рис. 3.11).
Если внутренняя схема двухполюсника содержит только пассивные элементы, то такой двухполюсник называется пассивным и в прямоугольнике ставится буква П, если внутренняя схема двухполюсника содержит активные элементы, то есть источники ЭДС или тока, то такой двухполюсник называется активным и в прямоугольнике ставится буква А.
Внутреннюю схему двухполюсника всегда можно разбить на участки, и эти участки, пользуясь теоремой о компенсации, заменить эквивалентными источниками. Тогда двухполюсник по отношению к выделенной ветви будет представлять собой некоторый эквивалентный генератор (рис. 3.12).
Тогда ток, протекающий в выделенной ветви, можно определить, используя формулу
Таким образом, всякий активный двухполюсник может быть заменен эквивалентным генератором с ЭДС Еэк и внутренним сопротивлением R эк. Для того чтобы токораспределение во внешней цепи не изменилось, должны соблюдаться следующие требования:
1) ЭДС эквивалентного генератора Еэк равна напряжению на зажимах ab двухполюсника при холостом ходе Еэк= Uabxx ;
2) внутреннее сопротивление эквивалентного генератора R эк равно эквивалентному сопротивлению двухполюсника относительно зажимов ab .
Таким образом, расчет цепи методом эквивалентного генератора сводится к определению параметров эквивалентного генератора Еэк и R эк.
Параметры эквивалентного генератора можно определить двумя способами: экспериментальным и расчетным.
Экспериментальный способ – это единственный путь определения параметров эквивалентного генератора, если неизвестна схема соединений двухполюсника. Суть его сводится к следующему.
1. При разомкнутых зажимах ab , то есть в режиме холостого хода ( R = ∞ и I = 0), измеряют напряжение на зажимах ab U а b хх. Согласно требованию 1 U а b хх = Еэк.
2. При замкнутых зажимах ab , то есть в режиме короткого замыкания ( R = 0), измеряют ток в выделенной ветви I кз (это можно сделать, отсоединив сопротивление R и подключив к зажимам ab амперметр, сопротивление которого мало, поэтому его можно считать замыкающим проводником).
Ток короткого замыкания связан с ЭДС источника соотношением
Расчетный способ применяется тогда, когда известна схема внутренних соединений двухполюсника и параметры входящих в нее сопротивлений и ЭДС. Рассмотрим этот способ на конкретном примере (рис. 3.13).
Выделяем нагрузочную ветвь с сопротивлением R н , заключая остальную часть схемы в прямоугольник. Эта часть схемы представляет собой двухполюсник с зажимами ab .
Мысленно закоротив источник ЭДС, находим эквивалентное сопротивление двухполюсника по отношению к зажимам ab , которое согласно требованию 2 равно внутреннему сопротивлению эквивалентного генератора:
3. Определим ЭДС эквивалентного генератора Еэк, равную напряжению на зажимах ab при холостом ходе. Для этого отсоединим сопротивление нагрузки, схема примет вид (рис. 3.14).
Так как ветвь с сопротивлением R 4 разомкнута, ток будет протекать только по контуру R 1→ R 3 → R 2, то есть
Напряжение на зажимах ab будет равно напряжению на зажимах cb :
Зная R эк и Еэк, находим ток в нагрузке
Нагрузка эквивалентного генератора согласно закону Джоуля – Ленца потребляет мощность, определяемую выражением
В режиме холостого хода ток равен нулю, следовательно, потребляемая мощность равна нулю. В режиме короткого замыкания нулю равно сопротивление нагрузки, следовательно, мощность так же не потребляется Р = 0. Таким образом, следует предположить, что в нагрузочном режиме с ростом сопротивления нагрузки мощность сначала увеличивается до некоторого максимального значения, а потом спадает до нуля (рис. 3.15).
Найдем условие, при котором нагрузка эквивалентного генератора потребляет максимальную мощность.
Мощность в нагрузке согласно закону Джоуля – Ленца определяется выражением
Подставим выражение для тока в формулу мощности:
Исследуем это выражение на экстремум. Функция имеет экстремум при условии равенства нулю ее первой производной.
Дробь равна нулю, если равен нулю числитель:
Преобразуем это выражение следующим образом:
Взяв вторую производную, можно доказать, что она отрицательна, следовательно, мощность максимальна при сопротивлении нагрузки, равном сопротивлению эквивалентного генератора. Такое сопротивление нагрузки Rc называется согласованным.
Максимальную мощность можно определить по формуле
На рис. 3.15 показано изменение мощности, потребляемой нагрузкой при изменении сопротивления нагрузки от нуля до бесконечности.
Электротехника ТОЭ
Лекции и задачи по ТОЭ. На сайте представлен лекционный материал для изучения теоретических основ электротехники и видеоуроки по всем темам. Так же тут можно заказать решение задач, курсовых, расчетных, контрольных и домашних работ. Онлайн помощь на экзамене, контрольной. Решение тестов, занятия по скайпу и др. В ближайшее время на сайт будут добавлены готовые работы на разные темы ТОЭ, ТАУ и другим дисциплинам.
Теория / 3.2. Методы расчета сложных электрических цепей / 3.2.6. Метод эквивалентного генератора
В некоторых случаях при расчете электрической цепи нас интересуют ток, напряжение, мощность только в какой-либо одной ветви схемы. Тогда, чтобы упростить задачу и не рассчитывать всю цепь, применяют метод эквивалентного генератора.
Прежде чем перейти к методу эквивалентного генератора, докажем теорему о компенсации.
Теорема о компенсации. Любой пассивный элемент электрической цепи можно заменить активным элементом, величина ЭДС которого равна падению напряжения на пассивном элементе, а направление противоположно направлению тока в нем.
Докажем эквивалентность такой замены. Рассмотрим для пимера схемы (рис. 3.9, а,б).
Заменим пассивный элемент R 1 источником ЭДС Е1.
Для схемы а запишем уравнение по второму закону Кирхгофа
Отсюда выразим ток в виде
Для схемы б второй закон Кирхгофа запишется в следующей форме:
Ток выразим в виде
При эквивалентной замене ток в сопротивлении R должен остаться неизменным, а он не изменится только в том случае, если E1=R1*I, что и требовалось доказать.
В любой электрической схеме всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от ее структуры, условно изобразить прямоугольником (рис. 3.10).
Например, выделим ветвь с сопротивлением R 5, а всю остальную часть заключим в прямоугольник.
Заключенную в прямоугольник часть схемы, которая двумя выводами подключается к выделенной ветви, называют двухполюсником.
Чаще всего нас не интересует часть схемы, заключенная в двухполюснике, и его обозначают прямоугольником с двумя выводами, к которым присоединяется интересующая нас ветвь (рис. 3.11).
Если внутренняя схема двухполюсника содержит только пассивные элементы, то такой двухполюсник называется пассивным и в прямоугольнике ставится буква П, если внутренняя схема двухполюсника содержит активные элементы, то есть источники ЭДС или тока, то такой двухполюсник называется активным и в прямоугольнике ставится буква А.
Внутреннюю схему двухполюсника всегда можно разбить на участки, и эти участки, пользуясь теоремой о компенсации, заменить эквивалентными источниками. Тогда двухполюсник по отношению к выделенной ветви будет представлять собой некоторый эквивалентный генератор (рис. 3.12).
Тогда ток, протекающий в выделенной ветви, можно определить, используя формулу
Таким образом, всякий активный двухполюсник может быть заменен эквивалентным генератором с ЭДС Еэк и внутренним сопротивлением R эк. Для того чтобы токораспределение во внешней цепи не изменилось, должны соблюдаться следующие требования:
1) ЭДС эквивалентного генератора Еэк равна напряжению на зажимах ab двухполюсника при холостом ходе Еэк= Uabxx ;
2) внутреннее сопротивление эквивалентного генератора R эк равно эквивалентному сопротивлению двухполюсника относительно зажимов ab .
Таким образом, расчет цепи методом эквивалентного генератора сводится к определению параметров эквивалентного генератора Еэк и R эк.
Параметры эквивалентного генератора можно определить двумя способами: экспериментальным и расчетным.
Экспериментальный способ – это единственный путь определения параметров эквивалентного генератора, если неизвестна схема соединений двухполюсника. Суть его сводится к следующему.
1. При разомкнутых зажимах ab , то есть в режиме холостого хода ( R = ∞ и I = 0), измеряют напряжение на зажимах ab U а b хх. Согласно требованию 1 U а b хх = Еэк.
2. При замкнутых зажимах ab , то есть в режиме короткого замыкания ( R = 0), измеряют ток в выделенной ветви I кз (это можно сделать, отсоединив сопротивление R и подключив к зажимам ab амперметр, сопротивление которого мало, поэтому его можно считать замыкающим проводником).
Ток короткого замыкания связан с ЭДС источника соотношением
Расчетный способ применяется тогда, когда известна схема внутренних соединений двухполюсника и параметры входящих в нее сопротивлений и ЭДС. Рассмотрим этот способ на конкретном примере (рис. 3.13).
Выделяем нагрузочную ветвь с сопротивлением R н , заключая остальную часть схемы в прямоугольник. Эта часть схемы представляет собой двухполюсник с зажимами ab .
Мысленно закоротив источник ЭДС, находим эквивалентное сопротивление двухполюсника по отношению к зажимам ab , которое согласно требованию 2 равно внутреннему сопротивлению эквивалентного генератора:
3. Определим ЭДС эквивалентного генератора Еэк, равную напряжению на зажимах ab при холостом ходе. Для этого отсоединим сопротивление нагрузки, схема примет вид (рис. 3.14).
Так как ветвь с сопротивлением R 4 разомкнута, ток будет протекать только по контуру R 1→ R 3 → R 2, то есть
Напряжение на зажимах ab будет равно напряжению на зажимах cb :
Зная R эк и Еэк, находим ток в нагрузке
Нагрузка эквивалентного генератора согласно закону Джоуля – Ленца потребляет мощность, определяемую выражением
В режиме холостого хода ток равен нулю, следовательно, потребляемая мощность равна нулю. В режиме короткого замыкания нулю равно сопротивление нагрузки, следовательно, мощность так же не потребляется Р = 0. Таким образом, следует предположить, что в нагрузочном режиме с ростом сопротивления нагрузки мощность сначала увеличивается до некоторого максимального значения, а потом спадает до нуля (рис. 3.15).
Найдем условие, при котором нагрузка эквивалентного генератора потребляет максимальную мощность.
Мощность в нагрузке согласно закону Джоуля – Ленца определяется выражением
Подставим выражение для тока в формулу мощности:
Исследуем это выражение на экстремум. Функция имеет экстремум при условии равенства нулю ее первой производной.
Дробь равна нулю, если равен нулю числитель:
Преобразуем это выражение следующим образом:
Взяв вторую производную, можно доказать, что она отрицательна, следовательно, мощность максимальна при сопротивлении нагрузки, равном сопротивлению эквивалентного генератора. Такое сопротивление нагрузки Rc называется согласованным.
Максимальную мощность можно определить по формуле
На рис. 3.15 показано изменение мощности, потребляемой нагрузкой при изменении сопротивления нагрузки от нуля до бесконечности.
Особенности метода эквивалентного генератора
- Т.к. МЭГ основан на принципе наложения, его можно применять только для линейных электрических цепей, для которых данный принцип работает. Для нелинейных цепей МЭГ применён быть не может.
- МЭГ работает на комплексных схемах замещения, т.е. только для какой-то одной частоты. Часто это бывают схемы для частоты сети (50 или 60 Гц) или это цепи постоянного тока (0 Гц).
- Из предыдущего замечания вытекает, что эквивалентные генераторы некорректно использовать в схемах расчёта переходных процессов в мгновенной форме.
- В качестве нагрузки эквивалентного генератора может выступать активная цепь. В этом случае нужно быть очень аккуратным при определении эквивалентной ЭДС.
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
Просто о сложном: суть метода симметричных составляющих в трёх предложениях Физически симметричные составляющие в электрических цепях не существуют. Симметричные составляющие введены для существенного упрощения расчёта…
Моделирование фильтра симметричных составляющих Симметричные составляющие – очень важные параметры, используемые в релейной защите для реализации защит различного оборудования.…
Законы Кирхгофа для расчёта электрических цепей При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие…
