Скорость звука в воздухе формула

Звук- калеб. движение в любой упругой матер. среде, вызван. каким-либо источником, проявл. в форме переод. изменений давления.

— материальная среда обладает упругостью и инерционностью

— в газах и жидкостях частицы колебл. в направлениях распространения волны

— в тверд.-перпендикулярно направлению распространения волны

Звуковая волна-процесс распростран.колебат.движения

Амплитуда-расстояние на кот. колеблится частица отклон. от положения равновесия.

y=A-sin · (wt+φ) – уравнение звуковой волны

w – круговая частота

Ухо человека воспринимает звук в диапазоне 20Гц-20000Гц

Геометрич. место точек, достигаемых в каждый момент волной – волновая поверхность (фронт)

Если фронт плоский, то волна – плоская, если сферический, то волна – сферическая

Особенности распространения звуковых волн в зависимости от температуры воздуха.

Скорость распространения звука в воздухе с= 331,45 кореньТ/273

Интерференция звуковых волн — наложения колеб. от нескольких источников

Звуковое поле – область про-ва в кот.колеб. звуковые волны.

Звуковое давление — Р-разность между мгновен.знач.полного давления и средним давлением, котор.наблюд.в среде при отсутствии звукового поля

р=Pm·sin (wt+ φ) ˂p˃=Па= н/м²

рэф=Рm·корень2 Рm- амплитуда давления

Интерференция — физическое явление, наблюдающееся при наложении нескольких волновых процессов и заключающееся в локальных отклонениях общей интенсивности от суммы интенсивностей входящих волн.

На распространение звуков в атмосфере влияет много факторов: температура на разных высотам, потоки воздуха. Эхо — это отраженный от поверхности звук. Звуковые волны могут отражаться от твердых поверхностей, от слоев воздуха в которых температура отличается от температуры соседних слоев.

Дифракция звука (лат. diffractus — буквально разломанный, переломанный) — явление, которое можно рассматривать как отклонение от законов геометрической оптики при распространении волн. Первоначально понятие дифракции относилось только к огибанию волнами препятствий, но в современном, более широком толковании, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн в неоднородных средах, а также при распространении ограниченных в пространстве волн.

Скорость звука — скорость распространения звуковыхволн в среде.

Как правило, в газахскорость звука меньше, чем вжидкостях, а вжидкостяхскорость звука меньше, чем в твёрдых телах.

Скорость звука в любой среде вычисляется по формуле:

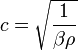
где β — адиабатическаясжимаемостьсреды; ρ — плотность.

Для газовэта формула выглядит так:

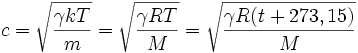
Физика 9 класс (Урок№15 — Звуковые волны. Скорость звука.)

где γ — показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных; k — постоянная Больцмана;R — универсальная газовая постоянная;T — абсолютная температуравкельвинах;t — температура в градусах Цельсия;m — молекулярная масса;M — молярная масса. По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул и в приближении постоянства показателя адиабаты пропорциональнаквадратному корнюиз абсолютной температуры.

Для твёрдых телскорость звука можно вычислить как:

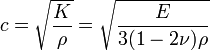
Где K — модуль всестороннего сжатия;E — модуль Юнга; ν —коэффициент Пуассона.

В воздухепринормальных условияхскорость звука составляет 331,46 м/с (1193 км/ч).

В водескорость звука составляет 1485 м/с. (см.Опыт Колладона-Штурма)

В твёрдых телахскорость звука составляет 2000—6500 м/с.

23. Звуковое поле и основные физические величины, характеризующие его. (Звуковое давление, плотность звукового поля). Звуковая мощность, интенсивность звука.

Плотность звукового поля, Д- это звуковая энергия, содержащаяся в единице объема среды D=р²/pc² p-плотность среды кг/м³; с-скорость звука в среде

Мощность звука p-количество звуковой энергии , излучаемой источником звука в единицу времени

Характер. источник звука или шума кол-во звуковой энергии, проходящей в 1с через площадь S, окружающую источник звука ˂р˃=Вм

Интенсивность звука, I-кол-во звуковой энергии, распространяемой в звуковом поле в единицу времени через единичную площадь (если в звуковом поле волны идут только в одном направлении)

I=р²/рс ˂I˃=Вт/м²; р-плотность среды рс-акустич.сопротивление среды (импедание) кг/м²с

Звуковое поле, область пространства, в которой распространяются звуковые волны, т. е. происходят акустические колебания частиц упругой среды (твёрдой, жидкой или газообразной), заполняющей эту область. З. п. определено полностью, если для каждой его точки известно изменение во времени и в пространстве какой-либо из величин, характеризующих звуковую волну: смещения колеблющейся частицы из положения равновесия, колебательной скорости частицы, звукового давления в среде; в отдельных случаях представляют интерес изменения плотности или температуры среды при наличии З. п. Понятие З. п. применяется обычно для областей, размеры которых порядка или больше длины звуковой волны.

С энергетической стороны З. п. характеризуется плотностью звуковой энергии (энергией колебательного процесса, приходящейся на единицу объёма); в тех случаях, когда в З. п. происходит перенос энергии, он характеризуется интенсивностью звука, т. е. средней по времени энергией, переносимой в единицу времени через единицу поверхности, перпендикулярной к направлению распространения волны.

Картина З. п. в общем случае зависит не только от акустической мощности и характеристики направленности излучателя — источника звука, но и от положения и свойств поверхностей раздела различных упругих сред, если такие поверхности имеются. В неограниченной однородной среде З. п. является полем бегущей волны. Вдали от источника в З. п. практически любого излучателя звуковое давление спадает по закону 1/r (где r — расстояния от источника .

Интенсивность звука (абсолютная) — величина, равная отношению потока звуковой энергии dP через поверхность, перпендикулярную направлению распространения звука, к площади dS этой поверхности:

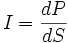
Для количественных сравнений громкости нужно ввести понятие интенсивности звука. Интенсивность звуковой волны определяется как средний поток энергии через единицу площади волнового фронта в единицу времени. Иначе говоря, если взять единичную площадку (например, 1 см 2 ), которая полностью поглощала бы звук, и расположить ее перпендикулярно направлению распространения волны, то интенсивность звука равна акустической энергии, поглощаемой за одну секунду. Интенсивность обычно выражается в Вт/см 2 (или в Вт/м 2 ).

Звуковое давление – разность между давлением, существующем в среде pср в данный момент, и атмосферным давлением pатм.

Измеряется в паскалях (сила в 1 Н, приложенная к площади 1 кв. м.). Атмосферное давление ~10 5 Па. Звуковые давления речи и музыки имеют величину до 100 Па.

. Как всякая сила, звуковое давление имеет направление. Однако, под давлением понимается сила, перпендикулярная к поверхности.

Скорость распространения звуковой волны (скорость звука) сзв в среде зависит от массы молекул или атомов и расстояния между ними. А они в свою очередь зависят от химического состава вещества, его температуры, а для газов и давления. Для технических расчетов достаточно считать

,

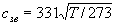
где Т — температура, К. При нормальном атмосферном давлении и Т=290 К (17 0 С) скорость звука 340 м/с.

Плотностью звуковой энергии e называется энергия, содержащаяся в единице объема среды распространения.

Время пробега волной единицы длины по лучу 1/сзв => e =I/сзв; [e]=[Вт/м 2 ]/[м/с]=[Вт*с/м 3 ]=[Дж/м 3 ].

Плотность энергии через давление:

.

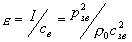
Плотность энергии в отличие от интенсивности величина скалярная, и поэтому может применяться и в тех случаях, когда определение лучей и волновых фронтов затруднительно или невозможно, например, при распространении звуковых волн в помещениях.

25. Уровень интенсивности звука и уровень звукового давления. Уровень звуковой мощности. Эквивалентный уровень звукового давления и эквивалентный уровень звука.

Единицы уровня звука Уровень интенсивности звука измеряют в десятых долях Белла(Б) – децибел (дБ)

Для различных уровней звукового давления – различные условия восприятия звука:

94- внутри вагона метро

Сложение уровней интенсивности звука

Пусть имеется n источников звука, каждый из которых в данной точке поля одну и ту же интенсивность звука I(первое), с уровнем интенсивности L(первое) L=lg·I(первое). Суммарная интенсивность звука I=I(первое) · n; Уровень суммарной интенсивности звука:

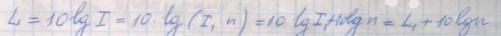
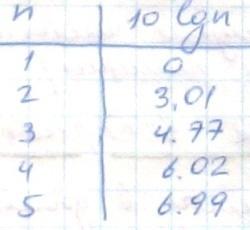
24. Закон Вебера – Фехнера и его интерпретация в акустике. Единицы уровня интенсивности звука. Сложение уровней интенсивности звука.

Для всех органов чувств человека ощущение пропорционально логарифму раздражителя, впряженному в единицах порога ощущения.

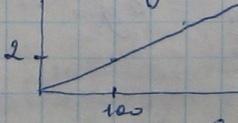
Свойства логарифмов log6a – показатель степени b которое надо возвести число b, чтобы получить число a.

Уровень интенсивности звука и уровень звукового давления. Диапазон изменения звукового давления

Уровень интенсивности звука

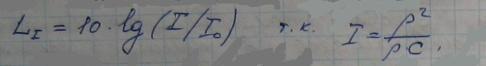
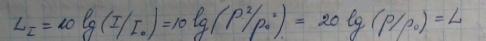
Уровень интенсивности звука, выраженный через звуковое давление

Пороговая величина звукового давления pₒ соответствует пороговой величине интенсивности звука Iₒ

рₒ=2 · 10(*в (– 5) степени)* Па; I0 =10 (*в – 12 степени*) Вт/м²; рₒ=10 (*в – 12 степени) Вт;

соотв.порогу слышимости на частоте 1000 Гц

При пороговых величинах уровень интенсивности звука и уровень давл.=0

Уровень звуковой мощности Lp=10·lg(p/pₒ) болевой порог: р=2·10²Па I=10² Вт/м² L=140 дБ

Нормальный разговор – 50-60 дБ

Практически тишина – 10 дБ

Порого слышимости мертвая тишина – 0дБ

НО: менее 20 дб трудно получить

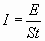
Интенсивностью волны I называют величину, численно равную средней по времени энергии Е, переносимой волной в единицу времени через единицу площади поверхности, расположенную перпендикулярно направлению распространения волны:

где S — площадь поверхности, через которую проходит волна, t — время ее прохождения через эту поверхность. Единица измерения интенсивности волны: Дж/(м 2 с) = Вт/м 2 .

Звук является объектом слуховых ощущений, поэтому оценивается человеком также субъективно. Субъективными характеристиками звука являются: высота -обусловленная частотой тона, тембр — определяется спектральным составом звука, громкость — уровень слухового ощущения, зависящая, прежде всего от I интенсивности звука. Следовательно объективными характеристиками звука являются: частота, интенсивность, акустический спектр. Человеческое ухо воспринимает звуки на частоте 1 кГц с интенсивностью не менее I0=10 -12 Вт/м 2 и называется интенсивность на пороге слышимости. Максимальная интенсивность звука на частоте 1 кГц, воспринимаемая человеком Iб=10 Вт/м 2 и называется болевым порогом, так как вызывает болевые ощущения. Различие между I0 и Iб очень велико (Iб/ I0 = 10 13 ), поэтому при измерениях удобно пользоваться логарифмической шкалой. В связи с этим вводят величину уровня интенсивности звука, равную десятичному логарифму отношения интенсивности исследуемого звука I к интенсивности I0 на пороге слышимости

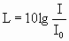
Уровень интенсивности звука измеряется в белах. бел — есть единица шкалы уровней интенсивности звука, соответствующая изменению интенсивности в 10 раз. Обычно применяют единицу в 10 раз меньшую, называемую децибелом (дБ). Тогда формула (4.11) принимает вид.

Если L=1 дБ, то 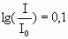, а. Таким образом, децибел соответствует таким двум уровням, интенсивности которых отличаются в 1,26 раза.

Согласно закону Вебера — Фехнера прирост силы ощущения пропорционален логарифму отношения интенсивностей двух сравнимых раздражений.

Закон Вебера — Фехнера лежит в основе создания шкалы уровней громкости, а также шкалы уровней интенсивности. результате область слышимости ограничена как сверху, так и снизу кривыми. Эти кривые получены на основании измерений, проведенных с людьми, обладающими наиболее чувствительными органами слуха. Для большинства людей область слышимости меньше; для многих частотная граница наступает при 18, 15 и даже при 10 кГц. Интенсивность в 10 -12 Вт/м 2 также ощущается далеко не всяким человеком. С возрастом область слышимости сужается. При повреждении уха она может стать совсем маленькой, а при глухоте сжимается в точку.

Для того чтобы найти соответствие между громкостью и интенсивностью звука на разных частотах, пользуются кривыми равной громкости. Видно, что среднее человеческое ухо наиболее чувствительно к частотам 2500 — 3000 Гц. Каждая промежуточная кривая отвечает одинаковой громкости, но разной интенсивности звука для разных частот. Используя совокупность кривых равной громкости, можно найти для разных частот громкости, соответствующие определенной интенсивности. Например, пусть интенсивность звука частотой 100 Гц равна 60 дБ

Звук

Перед тем, как приступить к рассмотрению темы, дадим определение такому явлению, как звук.

Удар молоточка по вилке вызывает возбуждение всей системы камертона с последующим звучанием чистого музыкального тона.

Гортань певца – по сути тоже акустический резонатор. Рисунок 2 . 7 . 2 демонстрирует спектры звуковых волн, издаваемых камертоном, струной пианино и низким женским голосом (альтом), звучащими на одной и той же ноте.

Рисунок 2 . 7 . 2 . Относительные интенсивности гармоник в спектре волну звука при звучании камертона ( 1 ) , пианино ( 2 ) и низкого женского голоса (альт) ( 3 ) на ноте «ля» контроктавы ( f 1 = 220 Г ц ) . По оси ординат отложены относительные интенсивности I I 0 .

Звуковые волны, чьи частотные спектры показаны на рисунке 2 . 7 . 2 , имеют одну и ту же высоту, но различные тембры.

Биения

Разберем также такое явление, как биения.

Биение – это явление, возникающее, когда две гармонические волны с близкими, но все же имеющими отличия частотами, накладываются друг на друга.

Биения сопровождают, к примеру, одновременное звучание двух струн, имеющих настройки практически одинаковой частоты. Человеческий орган слуха воспринимает биения как гармонический тон с громкостью, периодически изменяющейся во времени. Запишем выражения, показывающие закономерность изменения звуковых давлений p 1 и p 2 , которые осуществляют воздействие на ухо:

p 1 = A 0 cos ω 1 t и p 2 = A 0 cos ω 2 t .

Для удобства примем, что амплитуды колебаний звуковых давлений являются одинаковыми и равны p 0 = A 0 0.

Согласно принципу суперпозиции полное давление, которое вызывается обеими волнами в каждый момент времени, есть совокупность звуковых давлений, задаваемых каждой волной в тот же момент времени. Запишем выражение, показывающее суммарное воздействие волн, используя тригонометрические преобразования:

p = p 1 + p 2 = 2 A 0 cos ω 1 — ω 2 2 t cos ω 1 + ω 2 2 t = 2 A 0 cos 1 2 ∆ ω t cos ω с р t ,

где ∆ ω = ω 1 — ω 2 , а ω с р = ω 1 + ω 2 2 .

Рисунок 2 . 7 . 3 ( 1 ) отображает, каким образом давления p 1 и p 2 зависимы от времени t . В момент времени t = 0 оба колебания находятся в фазе, и их амплитуды суммируются. Поскольку частоты колебаний имеют хоть и небольшие, но отличия, через некоторое время t 1 колебания войдут в противофазу. В этот момент суммарная амплитуда станет равна нулю: колебания взаимно «погасятся». К моменту времени t 2 = 2 t 1 колебания вновь окажутся в фазе и т. д. (рисунок 2 . 7 . 3 ( 2 ) ).

Период биений Т б – это минимальное значение интервала между двумя моментами времени, которым соответствуют максимальная и минимальная амплитуда колебаний.

Формула, которая определяет медленно изменяющуюся амплитуду A результирующего колебания, имеет запись:

A = 2 A 0 cos 1 2 ∆ ω t .

Период Т б изменения амплитуды равен 2 π Δ ω . Мы можем это продемонстрировать, приняв следующее предположение: периоды колебаний давлений в звуковых волнах T 1 и T 2 являются такими, что T 1 < T 2 (т. е. ω 1 >ω 2 ). За период биений Т б наблюдается некоторое число n полных циклов колебаний первой волны и ( n – 1 ) циклов колебаний второй волны:

T б = n T 1 = ( n — 1 ) T 2 .

T б = T 1 T 2 T 2 — T 1 = 2 π ω 1 — ω 2 = 2 π ∆ ω или f б = 1 T б = 1 T 1 — 1 T 2 = f 1 — f 2 = ∆ f .

f б есть частота биений, определяемая как разность частот Δ f двух звуковых волн, которые воспринимаются ухом одновременно.

Органы слуха человека способны к восприятию звуковых биений до частот 5 – 10 Г ц . Прослушивание биений – это важный элемент техники настройки музыкальных инструментов.

Рисунок 2 . 7 . 3 . Биения, возникающие, когда накладываются две звуковые волны с близкими частотами.

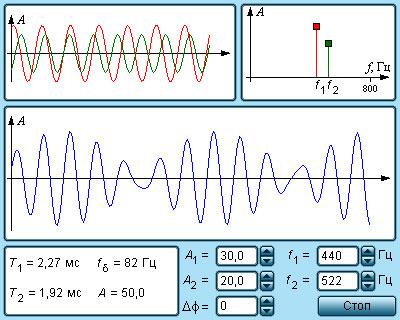
Рисунок 2 . 7 . 4 . Модель явления биений.

Скорость звука

Ско́рость зву́ка, скорость распространения в среде упругих волн . Определяется упругостью и плотностью среды. Для плоской гармонической волны в среде без дисперсии скорость звука равна c = ω / k > c = ω / k , где ω omega ω – частота , k boldsymbol k – волновое число . Со скоростью c c распространяется фаза гармонической волны, поэтому её называют также фазовой скоростью звука. В средах с дисперсией звука фазовая скорость различна для разных частот; в этих случаях используют понятие групповой скорости . При больших амплитудах упругой волны скорость распространения каждой точки профиля волны зависит от величины давления в этой точке, возрастая с ростом давления, что приводит к искажению формы волны (см. в статье нелинейная акустика ). Скорость звука в газах меньше, чем в жидкостях , а в жидкостях, как правило, меньше, чем в твёрдых телах . При температуре 20 °C и нормальном давлении скорость звука в воздухе составляет 343,1 м/c, в воде – 1490 м/c.

В газах и жидкостях звук распространяется в виде объёмных волн сжатия – разряжения. Если процесс распространения звука происходит адиабатически , то скорость звука равна c = x ( ∂ P / ∂ ρ ) s text= sqrt> c = x ( ∂ P / ∂ ρ ) s ​

​ , где P P – давление, ρ rho ρ – плотность вещества, индекс s s показывает, что производная берётся при постоянной энтропии . Эта скорость звука называется адиабатической.

В идеальном газе c = γ P / ρ = γ R T / μ =sqrt=sqrt c = γ P / ρ

​ , где R R – универсальная газовая постоянная , Т textit Т – абсолютная температура, μ mu μ – молекулярная масса газа, γ gamma γ – отношение теплоёмкостей при постоянном давлении и постоянном объёме. Это т. н. лапласова скорость звука; в газе она совпадает по порядку величины со средней тепловой скоростью движения молекул. Величина c ′ = P / ρ >=sqrt c ′ = P / ρ

​ называется ньютоновой скоростью звука; она определяет скорость звука при изотермическом процессе распространения, который имеет место на очень низких частотах.

В идеальном газе при заданной температуре скорость звука не зависит от давления и растёт с ростом температуры как T sqrt> T

​ . При комнатной температуре относительное изменение скорости звука в воздухе составляет примерно 0,17 % на 1 °C. В жидкостях скорость звука, как правило, уменьшается с ростом температуры. Исключением является вода , в которой скорость звука при комнатной температуре увеличивается с ростом температуры, достигает максимума при температуре ≈ 74 approx 74 ≈ 74 °C и уменьшается с дальнейшим ростом температуры. Скорость звука в воде растёт с увеличением давления примерно на 0,01 % на 1 атм, а также с увеличением содержания растворённых в ней солей .

В морской воде скорость звука зависит от температуры, солёности и глубины. Эти зависимости имеют сложный вид; для расчёта скорости звука используются таблицы, рассчитанные по эмпирическим формулам. Поскольку температура, давление, а иногда и солёность меняются с глубиной, то скорость звука в океане является функцией глубины. Эта зависимость в значительной степени определяет характер распространения звука в океане, в частности определяет существование подводного звукового канала .

В неограниченной твёрдой среде распространяются продольные и сдвиговые (поперечные) упругие волны. В изотропном твёрдом теле фазовая скорость для продольной волны

c l = E ( 1 − σ ) ρ ( 1 + σ ) ( 1 − 2 σ ) = K + 4 / 3 G ρ , >=sqrt< frac> =sqrt< frac>, c l ​ = ρ ( 1 + σ ) ( 1 − 2 σ ) E ( 1 − σ ) ​

​ , для сдвиговой волны

c t = E 2 ρ ( 1 + σ ) = G ρ , >=sqrt< frac> =sqrt< frac>, c t ​ = 2 ρ ( 1 + σ ) E ​

где E E – модуль Юнга , G G – модуль сдвига, σ sigma σ – коэффициент Пуассона , K K – модуль объёмного сжатия. Скорость распространения продольных волн всегда больше, чем скорость сдвиговых волн, причём обычно выполняется соотношение c l > 2 c t >>sqrt > c l ​ > 2

​ c t ​ . В монокристаллах скорость звука зависит от направления распространения волны в кристалле (см. статью Кристаллоакустика ). В тех направлениях, в которых возможно распространение чисто продольных и чисто поперечных волн, в общем случае имеется одно значение c l > c l ​ и два значения c t > c t ​ . Если значения c t > c t ​ различны, то соответствующие волны иногда называют быстрой и медленной поперечными волнами. В общем случае для каждого направления распространения волны в кристалле могут существовать три смешанные волны с различными скоростями распространения, которые определяются соответствующими комбинациями модулей упругости.

В металлах и сплавах скорость звука существенно зависит от предшествующей механической и термической обработки; это явление частично связано с дислокациями , наличие которых также влияет на скорость звука. В металлах, как правило, скорость звука уменьшается с ростом температуры. При переходе металла в сверхпроводящее состояние величина ∂ c ∂ T frac ∂ T ∂ c ​ в точке перехода меняет знак. В сильных магнитных полях проявляются некоторые эффекты в зависимости скорости звука от магнитного поля, отражающие особенности поведения электронов в металле.

Измерения скорости звука используются для определения многих свойств вещества, таких как величина отношения теплоёмкостей для газов, сжимаемости газов и жидкостей, модулей упругости твёрдых тел, температуры Дебая и др. Измерение малых изменений скорости звука – чувствительный метод определения примесей в газах и жидкостях. В твёрдых телах измерение скорости звука и её зависимости от температуры, магнитного поля и других параметров позволяет исследовать строение вещества: зонную структуру полупроводников , форму ферми-поверхности в металлах и многое другое.

Редакция физических наук

Опубликовано 4 мая 2023 г. в 18:54 (GMT+3). Последнее обновление 4 мая 2023 г. в 18:54 (GMT+3). Связаться с редакцией

Эпилог

В данном труде ученые определили, что важнейшую роль в оценке максимально возможной скорости звука играют две фундаментальные константы — постоянная тонкой структуры и отношение массы протона к массе электрона.

Проведенные расчеты были проверены на практике с применением разнообразных материалов. Эксперименты позволили установить, что скорость звука должна уменьшаться с атомарной массой. Из этого следует, что максимальная скорость звука достигается в твердом атомарном водороде, который может существовать в таком виде лишь при очень высоком давлении. Тем не менее было установлено, что верхняя граница скорости звука в рамках данного исследования составляет 36100 м/с. С практической точки зрения, подобные исследования крайне важны для понимания тех или иных материалов, а также их свойств.

Естественно, ученые не намерены останавливаться на достигнутом. Их расчеты и соответствующие экспериментальные данные требуют перепроверки, уточнения и дополнительного подтверждения. В будущем данное исследование будет продолжено, а верхняя граница скорости звука может неожиданно сместиться в большую или меньшую сторону ввиду новых данных. Как бы то ни было, фундаментальный подход остается прежним, а сам факт лучшего понимания процессов, протекающих вокруг нас, позволяет с уверенностью смотреть на развитие данного исследования.

Благодарю за внимание, оставайтесь любопытствующими и хорошей всем рабочей недели, ребята. 🙂

Немного рекламы

Спасибо, что остаётесь с нами. Вам нравятся наши статьи? Хотите видеть больше интересных материалов? Поддержите нас, оформив заказ или порекомендовав знакомым, облачные VPS для разработчиков от $4.99, уникальный аналог entry-level серверов, который был придуман нами для Вас: Вся правда о VPS (KVM) E5-2697 v3 (6 Cores) 10GB DDR4 480GB SSD 1Gbps от $19 или как правильно делить сервер? (доступны варианты с RAID1 и RAID10, до 24 ядер и до 40GB DDR4).

Dell R730xd в 2 раза дешевле в дата-центре Equinix Tier IV в Амстердаме? Только у нас 2 х Intel TetraDeca-Core Xeon 2x E5-2697v3 2.6GHz 14C 64GB DDR4 4x960GB SSD 1Gbps 100 ТВ от $199 в Нидерландах! Dell R420 — 2x E5-2430 2.2Ghz 6C 128GB DDR3 2x960GB SSD 1Gbps 100TB — от $99! Читайте о том Как построить инфраструктуру корп. класса c применением серверов Dell R730xd Е5-2650 v4 стоимостью 9000 евро за копейки?

• скорость света
• скорость звука
• максимальная скорость
• водород
• межатомные связи
• твёрдое тело
• давление
• звуковые волны
• масса протона
• масса электрона
• константы

• Блог компании ua-hosting.company
• Научно-популярное
• Физика
• Химия

Скорость звука. Распространение звука.
материал по физике

Мы знаем, что звук распространяется по воздуху. Именно потому мы и можем слышать. В вакууме никаких звуков существовать не может. Но если звук передается по воздуху, вследствие взаимодействия его частиц, не будет ли он передаваться и другими веществами? Будет.

Распространение и скорость звука в разных средах

Звук передается не только воздухом. Наверное, все знают, что если приложить ухо к стене, то можно услышать разговоры в соседней комнате. В данном случае звук передается стеною. Звуки распространяются и в воде, и в других средах. Более того, распространение звука в различных средах происходит по-разному. Скорость звука различается в зависимости от вещества.

Любопытно, что скорость распространения звука в воде почти в четыре раза выше, чем в воздухе. То есть, рыбы слышат «быстрее», чем мы. В металлах и стекле звук распространяется еще быстрее. Это происходит потому, что звук это колебания среды, и звуковые волны передаются быстрее в средах с лучшей проводимостью.

Плотность и проводимость воды больше, чем у воздуха, но меньше, чем у металла. Соответственно, и звук передается по-разному. При переходе из одной среды в другую скорость звука меняется.

Длина звуковой волны также меняется при ее переходе из одной среды в другую. Прежней остается лишь ее частота. Но именно поэтому мы и можем различить, кто конкретно говорит даже сквозь стены.

Так как звук это колебания, то все законы и формулы для колебаний и волн хорошо применимы к звуковым колебаниям. При расчете скорости звука в воздухе следует учитывать и то, что эта скорость зависит от температуры воздуха. При увеличении температуры скорость распространения звука возрастает. При нормальных условиях скорость звука в воздухе составляет 340 344 м/с.

Звуковые волны, как известно из физики, распространяются в упругих средах. Именно поэтому звуки хорошо передаются землей. Приложив ухо к земле, можно издалека услышать звук шагов, топот копыт и так далее.

В детстве все наверняка развлекались, прикладывая ухо к рельсам. Стук колес поезда передается по рельсам на несколько километров. Для создания обратного эффекта звукопоглощения, используют мягкие и пористые материалы.

Например, чтобы защитить от посторонних звуков какое-либо помещение, либо, наоборот, чтобы не допустить выхода звуков из комнаты наружу, помещение обрабатывают, звукоизолируют. Стены, пол и потолок обивают специальными материалами на основе вспененных полимеров. В такой обивке очень быстро затихают все звуки.

Еще один пример различной проводимости это рыбалка. Звуки в воде распространяются очень хорошо и быстро. Именно по этой причине, чтобы не распугать рыбу, необходимо соблюдать тишину и не стучать, и не топать. Рыба очень чувствительна к таким колебаниям и быстро уплывает, чувствуя опасность.

Скорость звука. Скорость распространения звука в воздухе.

В статье рассмотрены характеристика звуковых явлений в атмосфере: скорость распространения звука в воздухе, влияние на распространение звука ветра, тумана.
Продольные колебания частиц материи, распространяясь по материальной среде (по воздуху, воде и твердым телам) и достигнув уха человека, вызывают ощущения, называемые звуком.
В атмосферном воздухе всегда находятся звуковые волны различной частоты и силы. Часть этих волн создается искусственно человеком, а часть звуков имеет метеорологическое происхождение.
К звукам метеорологического происхождения относятся гром, завывание ветра, гудение проводов, шум и шелест деревьев, «голос» моря, звуки при падении на земную поверхность твердых и жидких осадков, звуки прибоя у берегов морей и озер и другие.
На скорость распространения звука в атмосфере влияет температура и влажность воздуха, а также ветер (направление и его сила). В среднем скорость звука в атмосфере равна 333 м/с. С увеличением температуры воздуха скорость звука несколько возрастает. Изменение абсолютной влажности воздуха оказывает меньшее влияние на скорость звука.
Скорость звука в воздухе определяется формулой Лапласа:

(1),
где р — давление; ? — плотность воздуха; c? — теплоемкость воздуха при постоянном давлении; cp — теплоемкость воздуха при постоянном объеме.
Используя уравнение состояния газа, можно получить ряд зависимостей скорости звука от метеорологических параметров.
Скорость звука в сухом воздухе определяется по формуле:
с0 = 20,1 ?Т м/с, (2)
а во влажном воздухе:
с0 = 20,1 ?ТВ м/с, (3)
где ТВ = так называемая акустическая виртуальная температура, которая определяется по формуле ТВ = Т (1+ 0,275 е/р).
При изменении температуры воздуха на 1° скорость звука изменяется на 0,61 м/с. Скорость звука зависит от величины отношения е/р (отношение влажности к давлению), но эта зависимость мала, и, например, при упругости водяного пара менее 7мм пренебрежение ею дает ошибку в скорости звука, не превышающую 0,5 м/сек.
При нормальном давлении и Т = 0 °С скорость звука в сухом воздухе равна 333 м/сек. Во влажном воздухе скорость звука может быть определена по формуле:
с = 333 + 0,6t + 0,07е (4)
В диапазоне температур (t) от -20° до +30° эта формула дает ошибку в скорости звука не более ± 0,5 м/сек. Из приведенных формул видно, что скорость звука повышается с повышением температуры и влажности воздуха.
Ветер оказывает сильное влияние: скорость звука по направлению движения ветра увеличивается, против ветра — уменьшается. Наличие ветра в атмосфере вызывает дрейф звуковой волны, что создает впечатление смещения источника звука. Скорость звука в этом случае (c1) определится выражением:
c1 = c + U cos ?, (1)
где U-скорость ветра; ? — угол между направлением ветра в точке наблюдения и наблюдаемым направлением прихода звука.
Знание величины скорости распространения звука в атмосфере имеет большое значение при решении ряда задач по изучению верхних слоев атмосферы акустическим методом. Пользуясь средней скоростью звука в атмосфере, можно узнать расстояние от своего местонахождения до места возникновения грома. Для этого нужно определить число секунд между видимой вспышкой молнии и моментом прихода звука грома. Затем надо умножить среднее значение скорости звука в атмосфере — 333 м/сек. на полученное число секунд.

Как устроен мир. Скорость звука. 343. 1453

Продолжим разговор о гармонических соотношениях в окружающем нас мире.

В предыдущих статьях под заголовком «Как устроен мир» мы узнали, что многие физические процессы прокалиброваны числами из ряда Кучина, который десятичным образом связан с числами ряда Фибоначчи (см. статью Пирамида чисел Фибоначчи – Кучина. Лестница к Солнцу.)

Поговорим о звуке, вернее о скорости звука. Мы живем в мире, где звук в основном приходит к нам по воздуху. В редком случае нам доводится услышать звуки, распространяющиеся в воде, еще реже в твердых телах. Но эти сведения весьма важны для гидроакустики — и военной и гражданской, сейсмологии, геологии.

Измерение скорости звука производили многие ученые 16-18 веков. Более того, появилась отдельная наука – акустика, которая затем раздробилась на ряд самостоятельных дисциплин – акустика воздушной среды, акустика моря,и т.д.

Проблема всех современных наук – и их одновременное достижение – все более и более сложный математический аппарат, в результате за эти лесом формул и экспериментов надежно укрылась та «поляна», на которой спокойно проживает простая истина.

Попробуем преодолеть этот математический лабиринт – и обратимся к иллюстрации.

На рис. 1 показана цитата из книги академика Папалекси «Курс физики», 1948 год (академик умер в 1947 – это посмертное издание). Папалекси справедливо пишет, что первым правильную формулу для скорости звука в среде дал Лаплас. Скорость звука при 0 градусов Цельсия и давлении 760 мм. рт. ст. у Папалекси по формуле Лапласа оказалась равной 332 м/сек. Запомним этот результат.

Обратимся к рис. 2 – это таблица из современного справочника «Акустика» под ред. Сапожкова, Москва, «Радио и связь», 1989.

Для воздуха при 0 градусов Цельсия скорость звука оказывается равна 331 м/сек, что несущественно отличается от данных Папалекси.

А далее сюрприз!

ДЛЯ ВОЗДУХА ПРИ 20 ГРАДУСАХ ЦЕЛЬСИЯ СКОРОСТЬ ЗВУКА ОКАЗЫВАЕТСЯ РАВНОЙ ТОЧНО 343 М/СЕК!

Напоминаю – 343 – число из ряда Кучина.

Пропускаем строчку для Гелия в таблице (эта строчка очень любопытна — звук в гелии распространяется очень быстро — это связано с тем, что он не образует двухатомных молекул) и обнаруживаем, что для воды пресной скорость звука равна 1430 м/сек, для воды с соленостью в 3,5% – 1500 м/сек.

Это означает, что в слабосоленой воде, например в устье Дона на Азовском море и в устье Невы на Балтийском море СКОРОСТЬ ЗВУКА В ВОДЕ ОЧЕНЬ БЛИЗКА К 1453 М/СЕК – ЧИСЛУ ИЗ РЯДА КУЧИНА.

Вот такие удивительные результаты.

Много занимался акустикой великий физик австриец Мах. На рис. 3 приведена фотография полета пули, сделанная Махом после 1886 и приведенная в его «Популярных лекциях по физике». Мах стрелял из специально сделанного австрийского ружья Манлихер, у которого скорость пули превышала скорость звука в воздухе. Величину скорости звука Мах определял, как 340 м/сек, вероятно он проводил опыты на высотах 200-300 метров над уровнем моря. Опыты Маха со стрельбой из ружья привели его к большому открытию – при превышении пулей скорости звука меняется динамика ее полета – образуется ударная волна. На фотографии она представляет собой параболу воздушной волны идущую перед пулей.

Через 60 лет, после открытия Маха, ударная звуковая волна создала множество проблем для конструкторов самолетов с реактивными двигателями.

Мах писал, что ударная волна образуется на скорости 340 м/сек, в настоящее время принято считать для авиации, что образование ударной волны и преодоление звукового барьера самолет у земли в среднем выполняет при скоростях звука чуть выше – т.е. 343-344 м/сек.

Соответственно скорости современных самолетов считают в числах Маха. Если самолет летит на бреющем полете со скоростью М=2,0 – это означает, что он летит на скорости (343-344) х 2 = 686 – 688 м/сек.

1. скорость звука в воздухе в нормальных условиях равна 343 м/сек – т.е. точно равна числу из ряда Кучина.
2. скорость звука в воде при малой солености может быть весьма близка к 1450-1460 м/сек, т.е. к числу 1453 из ряда Кучина.
3. физика полета в воздушной среде изменяется на границе скоростей равных скорости звука – для нормальных условий это около 343-344 м/сек – практически на рубеже числа 343 из ряда Кучина.

Простые численные соотношения известны человечеству давно.
Но Ваши числа не простые и, тем не менее, вопрос: эти простые соотношения изначально существуют в Природе или мы упрощаем, чтобы понимать, или это просто забава?

Соотношения о которых я пишу — это вовсе не забава. Дело в том, что ОТНОСИТЕЛЬНЫЕ или ПРОПОРЦИОНАЛЬНЫЕ закономерности — они вполне объяснимы некими целесообразностями, но я показываю ПРЯМЫЕ АБСОЛЮТНЫЕ ПОПАДАНИЯ многих законов природы в числа ряда Кучина. Именно не числа ряда Кучина составлены из этих законов, а законы их содержат. У меня есть объяснение этому — вполне научное, но оно не такое простое, чтобы его помещать в комментарии. К тому же это гипотеза, а я стараюсь оперировать фактами. Спасибо за интерес к публикации.

Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.

Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.

Урок№31. Распространение звука. Звуковые волны. Скорость звука

Всем вам известно, что звук передаётся от источника не мгновенно, а спустя некоторый промежуток времени (вспомните хотя бы грозу, когда мы сначала видим молнию, а лишь затем до нас доносятся раскаты грома).

— Так как же происходит распространения звуковых колебаний?

Итак, мы уже знаем, что любое звучащее тело совершает колебания. Так вот, его колебания передаются прилежащим частицам воздуха, которые тоже начинают колебаться и передают колебания соседним частицам, а эти в свою очередь передают колебания дальше и так далее. Мы уже с вами знаем, что процесс распространения колебаний в среде называется механической волной. Значит звук — это тоже волна, которую мы будем называть звуковой.

Достигнув уха, звуковая волна поступает в слуховой проход и достигает барабанной перепонки, которая начинает вибрировать.

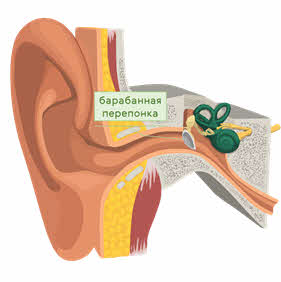
В барабанной полости расположены три слуховые косточки: молоточек, наковальня и самая маленькая косточка нашего организма — стремечко.

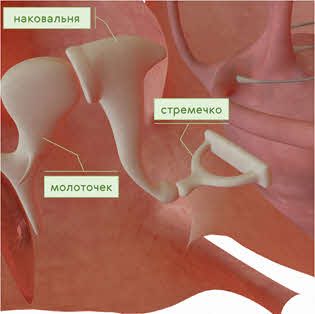
Механические колебания барабанной перепонки передаются слуховым косточкам – сначала молоточку, затем наковальне и стремечку. От них колебания передаются во внутреннее ухо. Оно представлено костным лабиринтом и состоит из трёх частей: преддверия, улитки и полукружных каналов органа равновесия.

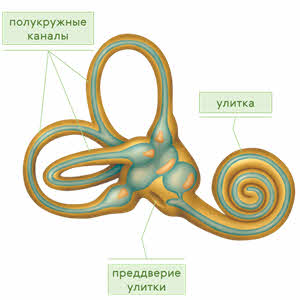
В улитке находится перепонка, на которой расположены двадцать три с половиной тысячи мельчайших волокон, которые проводят слуховое раздражение к коре головного мозга.

Как мы видели, колебания частиц среды, в которой распространяется звуковая волна, совершают колебания в направлении её распространения. Следовательно, звуковая волна — это продольная волна сжатия и разрежения. А мы уже с вами знаем, что продольные волны могут распространяться в любой среде: твёрдой, жидкой и газообразной.

— А распространяется ли звук в вакууме?

Впервые установить экспериментально, передаётся ли звук в безвоздушном пространстве, удалось в тысяча шестьсот шестидесятом году Роберту Бойлю. Для этого он использовал вакуумный насос, изобретённый им же в 1657 году.

Суть опыта такова. Бойль поместил в сосуд вакуумного насоса работающий будильник (мы, для большей наглядности, используем электрический звонок). Звук, издаваемый под колоколом насоса, стал тише, но всё же был вполне различим. Затем Бойль начал откачивать воздух из сосуда с часами. Звук будильника начал постепенно слабеть, пока совсем не исчез. Но, обратите внимание, что молоточек звонка продолжает ударять по звонковой чаше. Значит, она колеблется, но эти колебания дальше не распространяются, так как нет передающей среды. Если впустить под колокол насоса воздух, то мы снова услышим звон.

Этот опыт доказал, что для распространения звука необходима среда. Среда, отделяющая нас от колеблющихся тел, — это обычно воздух. Но, как мы уже говорили, звук может также распространяться в жидкой и твёрдой среде. Так под водой хорошо слышны звуки, издаваемые водными транспортными средствами, удары камней и так далее. А показать распространение звука в твёрдых телах можно на таком опыте. Возьмите механические часы и деревянную доску. Если положить часы на один конец деревянной доски, а к другому концу доски приложить ухо, можно ясно услышать тиканье.

Приведём ещё несколько примеров. Возьмите металлическую ложку и привяжите к ней конец бечёвки. А второй конец бечёвки приложите к уху. Если ударить по ложке, то можно услышать довольно сильный звук.

Звук будет более громким, если вместо бечёвки использовать какую-либо проволоку. Но мы совсем не услышим звука, если ложку привязать к резиновому шнуру́ и повторить эксперимент.

Способность различных тел передавать звуковые колебания называется звукопроводностью.

Из результатов наших опытов следует, что мягкие и пористые тела очень плохо проводят звук. Поэтому, чтобы защитить помещение от проникновения посторонних звук, его стены, пол и потолок прокладывают прослойками звукопоглощающих материалов.

Таким образом, звуковые волны распространяются в твёрдых телах, жидкостях и газах, но не могут распространяться в безвоздушном пространстве, то есть в вакууме.

Звуковые волны, так же, как и механические, характеризуются скоростью распространения. Именно поэтому во время грозы мы сначала видим вспышку молнии и лишь через некоторое время до нас доносятся раскаты грома.

Но гром и молния происходят в один и тот же момент времени, а запаздывание возникает из-за того, что скорость звука в воздухе существенно меньше скорости света, идущего от молнии. Вы знаете, что скорость света относится к фундаментальным физическим постоянным и примерно равна 300 000 км/с. Поэтому вспышку молнии мы видим практически в момент её возникновения. А вот звук грома доходит до нас со скоростью примерно в 340 м/с.

Кстати, первые попытки экспериментально определить скорость звука начались ещё в начале семнадцатого века. В трактате «Новый Органон» Фрэнсис Бэкон указал на возможность определения скорости звука путём сравнения времени, между вспышкой света и звуком выстрела.

В 1636 году французский физик Марен Мерсенн предпринял первые попытки экспериментального определения скорости звука. Для этого производился выстрел из пушки, а затем измерялось время, прошедшее между моментами, когда наблюдатель замечал вспышку, и моментом, когда до него доносился отзвук выстрела. Разделив расстояние, покрытое звуковой волной за полученное время, учёный получил скорость звука, равную 450 м/с.

Более точные измерения были произведены в Италии в 1660 году. На это раз для опыта друг напротив друга были поставлены две пушки. Первая пушка производила выстрел, после чего измерялось время между вспышкой и моментом, когда звук выстрела достигал второй пушки. Затем, аналогичные измерения делали и для второй пушки. В качестве скорости звука было определено расстояние между пушками, делённое на среднее время экспериментов. Таким образом исключалось влияние ветра на скорость распространения звука.

Лишь в 1809 году Пьер-Симоном де Лапласом была получена формула для теоретических расчётов скорости звука в воздухе.

— А от чего зависит скорость звука?

Конечно же скорость звука зависит от того, в какой среде он распространяется. Как показали различные измерения, скорость звука в твёрдых телах и жидкостях гораздо больше, чем в воздухе.

Благодаря тому, что твёрдые тела хорошо проводят звуковые волны, возможно обучение глухих людей игре на музыкальных инструментах и танцам. Вибрация пола, корпуса музыкального инструмента позволяет глухим людям распознавать музыкальные такты и даже ноты. А в давние времена в крепостных стенах помещали «слухачей», которые по звуку, передаваемому землёй, могли определить, ведёт ли враг подкоп к стенам или нет. Слухачи часто использовались во время войн. Но с появлением радиолокации профессия отмерла. Однако есть несколько интересных историй, одна из которых связана с блокадой Ленинграда, где для работы на акустических аппаратах были задействованы незрячие люди, обладающие исключительным слухом. Уже в первые месяцы службы им удалось добиться огромных успехов. Они узнавали о приближении фашистских самолётов за несколько десятков километров до того, как те появлялись в небе над Ленинградом. При этом слепые слухачи легко отличали советские самолёты от немецких и, более того, по шуму мотора сообщали зенитчикам тип приближающихся самолётов. Так как самолёты тогда летали медленнее, чем сейчас, то времени для подготовки к отражению налёта у зенитчиков было предостаточно.

Скорость звука зависит и от температуры среды: с увеличением температуры она возрастает, и наоборот. Конечно, в рамках небольшого изменения температуры скорость меняется незначительно. На качественном уровне этот факт можно объяснить тем, что при низких температурах скорость молекул газа меньше и процесс переноса колебательного процесса молекул также уменьшается.

Поскольку звук — это волна, то для определения его скорости можно пользоваться формулами:

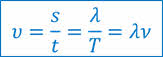
Закрепления материала.