Счетчики — устройства предназначенные для подсчета числа сигналов, поступающих на его вход и фиксация этого числа в виде кода хранящегося в триггерах. Количество разрядов счетчика определяется наибольшим числом, которое должно быть получено в каждом конкретном случае. Для подсчета и выдачи результата счетчики имеют один вход и n выходов, где n-количество разрядов. В общем случае счетчик имеет 2? устойчивых состояния, включая и 0-е. Количество устойчивых состояний называется коэффициентом пересчета счетчика (М= 2?). По назначению счетчики подразделяются на: простые и реверсивные.
Простые счетчики- счетчики, работающие только на сложение или вычитание. Суммирующий счетчик предназначен для выполнения счета в прямом направление, т.е. с приходом очередного сигнала показатель счетчика увеличивается на 1. Вычитающий счетчик предназначен для счета в обратном направлении, т.е. с приходом нового сигнала счетчик уменьшается на 1. счетчик сигнал триггер реверсный
Реверсивный счетчик может работать и на сложение и на вычитание.
По способу организации счета счетчики бывают: асинхронные или синхронные.
По способу организации цепей переноса между разрядами счетчика счетчики бывают: последовательные, параллельные и частичнопараллельные.
Двоичный счетчик с параллельным переносом.
Общие сведения о счетчиках
Счётчики относятся к функциональным узлам последовательностного типа, логическое состояние которых определяется последовательностью поступления входных сигналов. Счётчики применяются в различных цифровых устройствах. Назначение счётчика очевидно: это подсчёт числа некоторых событий или временных интервалов, либо упорядочение событий в хронологической последовательности. Счётчики могут выполнять и другие функции, например, их можно использовать для адресации, в качестве делителей частоты и элементов памяти.
Счётчик характеризуются прежде всего модулем счёта (ёмкостью) М. Он переходит при поступлении входных сигналов из состояния в состояние, после каждых М сигналов возвращаясь к началу цикла. Счётчики классифицируют по значению модуля, направлению счёта, способу организации межразрядных связей, по способу подачи тактового импульса.
По значению модуля счёта различают двоичные (М=2n), двоично-кодированные (с произвольным модулем, но кодированием состояний двоичными кодами), счётчики с одинарным кодированием и др.
По направлению счёта счётчики делят на суммирующие (прямого счёта), вычитающие (обратного счёта) и реверсивные (с изменением направления счёта).
По способу организации межразрядных связей различают счётчики с последовательным, параллельным и комбинированными переносами. Параллельные счётчики называют синхронными, а последовательные — асинхронными.
Цифровую схему, выполняющую функцию счёта, можно собрать из триггеров. Рассмотрим некоторые схемы счётчиков.
Счетчики электроэнергии. Устройство, принцип действия и подключение счетчиков энергии.
Счётчики со сквозным переносом
Процедура двоичного и десятичного счёта показана в табл. 13.1. Используя 4 двоичных разряда (D, C, B и A) можно считать от 0000 до 1111 (от 0 до 15 в десятичной системе). Столбец А соответствует самому младшему разряду, а столбец D самому старшему разряду. Если нужен счётчик, который считает от 0000 до 1111 (в двоичной системе), у него должно быть 16 различных выходных состояний, т.е. нужен счётчик с модулем 16. На рис.13.1 показана схема счётчика по модулю 16, составленная из 4 JK‑триггеров. Каждый JK‑триггер работает в режиме переключения (J=K=1). Пусть в начальный момент состояние выходов счётчика соответствует двоичному числу 0000 (счётчик очищен). При поступлении тактового импульса 1 на синхронизирующий вход (C) триггера T1 этот триггер переключается (при прохождении среза импульса) и на индикаторе появляется двоичное число 0001. Тактовый импульс 2 возвращает триггер T1 в исходное состояние 0 (Q=0), что в свою очередь приводит к переключению триггера T2 в состояние 1 (Q=1). На индикаторе появится число 0010. Счёт продолжается: срез сигнала на выходе каждого триггера запускает следующий триггер.
Таблица двоичного и десятичного счета
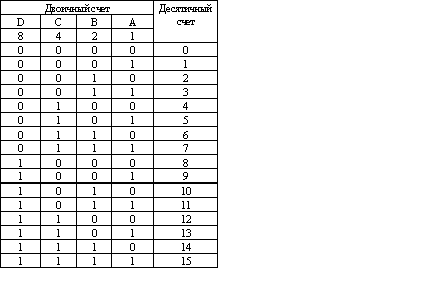
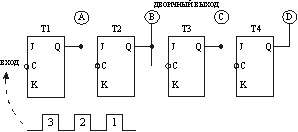
Рис.13.1. Схема счетчика по модулю 16
Из табл.13.1 видно, что цифры (1 или 0) в столбце А изменяется на каждом шаге счёта, т.е. триггер T1 переключается с приходом каждого нового тактового импульса. Из столбца В видно, что триггер T2 переключается в два раза реже триггера T1. Каждый более старший разряд «переключается» в 2 раза реже предыдущего.
На рис.13.2 показаны временные диаграммы при работе счётчика в процессе счёта до 10 (двоичное число 1010).

Рис.13.2. Временные диаграммы работы счетчика по модулю 16
Синхронизирующему входу состветствует верхняя диаграмма. Диаграммы для выходов Q триггеров T1, T2, T3, T4 приведены ниже. Под диаграммами указаны двоичные числа, соответствующие различным состояниям счётчика. Из рис.13.2 видно, что тактовые импульсы запускают только триггер T1, триггер T1 запускает триггер T2, триггер T2 запускает триггер T3 и т.д. Каждый триггер воздействует только на один (следующий за ним триггер), поэтому для переключения всех триггеров необходимо некоторое время. Например, на импульсе 8 (рис.13.2) тактовый импульс запускает триггер T1, вызывая его переключение в состояние 0. Это в свою очередь приводит к переключению триггера T2 из состояния 1 в состояние 0. Затем точно также переключается T3. В момент установки на выходе Q триггера T3 уровня логического 0 запускается триггер T4, который переключается из состояния 0 в состояние 1. Таким образом, изменение состояний последовательно распространяется по цепочке триггеров. Рассматриваемый счётчик называют счётчиком со сквозным переносом. Кроме этого данный счётчик можно назвать асинхронным, поскольку предыдущий триггер вырабатывает для последующего тактовые импульсы. По направлению счёта счётчик, изображённый на рис.13.1 является суммирующим (прямого счёта).
Асинхронные счётчики по модулю 10
Счётчик по модулю 10 считает от 0000 до 1001 (от 0 до 9 в десятичной системе), т.е. до черты в табл.13.1. Для построения такого счётчика трёх триггеров недостаточно (10>23), поэтому он содержит 4 триггера, но имеет обратные связи, останавливающие счёт при коде 9=1001. На рис.13.3 показана схема счётчика по модулю 10, в которую кроме 4 триггеров включён логический элемент И‑НЕ, для установки всех триггеров в нулевое состояние (очистки счетчика) с приходом десятого импульса.
Рис.13.3. Схема асинхронного счетчика по модулю 10
Рассмотрим принцип работы данной схемы (рис.13.3). Из табл.13.1 видно, что за числом 1001 следует 1010 (10 в десятичной системе). При подаче логической 1, содержащейся в разрядах двоек и восьмерок двоичного числа 1010, на входы элемента И‑НЕ, этот элемент подаст логический 0 на входы R четырех триггеров. Таким образом, все триггеры установятся в состояние 0 и счетчик снова начинает считать от 0000 до 1010. Подобное использование логического элемента И‑НЕ позволяет создать счетчики с некоторыми другими значениями модуля. Счетчик, изображенный на рис.13.3 называют также декадным (десятичным) счетчиком.
В синхронных счетчиках все триггеры получают тактовый импульс одновременно, поскольку тактовые входы их соединяются параллельно. Такие триггеры переключаются практически одновременно. В асинхронных счетчиках каждый триггер вносит в процесс счета определенную задержку, поэтому младшие разряды результирующего кода появляются на выходах триггеров не одновременно, т.е. несинхронно с соответствующим тактовым импульсом. Например, для четырехразрядного асинхронного счетчика код 1111 появится на выходах триггеров уже после того, как поступит шестнадцатый тактовый импульс. Код 1111 сформируется не одновременно.
Рассмотрим схему 3‑разрядного счетчика по модулю 8 (рис.13.4). Все синхронизирующие входы триггеров (C) соединены параллельно, тактовые импульсы поступают непосредственно на синхронизирующий вход каждого триггера.
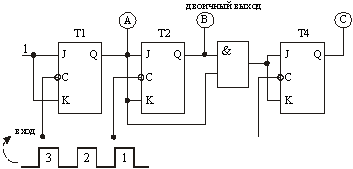
Рис.13.4. Схема синхронного счетчика по модулю 8
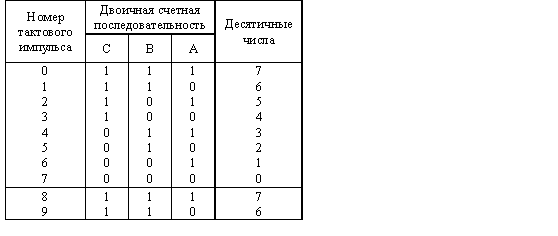
Последовательность двоичных чисел, проходимая счетчиком за один цикл счета (счетная последовательность) приведена в табл.13.2.
Счетная последовательность импульсов

Рассмотрим принцип работы данного счетчика в течение одного цикла счета. На каждом шаге цикла входной импульс поступает на синхронизирующий вход каждого триггера.
Импульс 1 — строка 2 табл.13.2. Переключается только триггер T1, поскольку только у него на входах J и K действует уровень логической 1. T1 переходит из состояния 0 в состояние 1.
Результат: на выходе счетчика 001.
Импульс 2 — строка 3. Переключаются два триггера T1 и T2, поскольку на входах J и K этих триггеров действует уровень логической 1. T1 переходит из состояния 1 в состояние 0, T2 — из состояния 0 в состояние 1.
Результат: на выходе 010.
Импульс 3 — строка 4. Переключается только один триггер. T1 переходит из состояния 0 в состояние 1. T2 не переключается, поскольку на входах J и K действует уровень логического 0.
Результат: на выходе 011.
Импульс 4 — строка 5. Все триггеры меняют свое состояние на противоположное. T1 и T2 переходят из 1 в 0. T3 переключается из 0 в 1.
Результат: на выходе 100.
Импульс 5 — строка 6. Триггер T1 переходит из состояния 0 в состояние 1.
Результат: на выходе 101.
Импульс 6 — строка 7. Переключаются два триггера. T1 переходит из 1 в 0, T2 — из 0 в 1.
Результат: на выходе 110.
Импульс 7 — строка 8. Триггер T1 переходит из состояния 0 в состояние 1.
Результат: на выходе 111.
Импульс 8 — строка 9. Все триггеры меняют свое состояние, переходя из 1 в 0.
Результат: на выходе 000.
Следует заметить, что в данном счетчике JK‑триггеры используются как в режиме переключения (J=K=1), так и в режиме блокировки (J=K=0).
Помимо суммирующих счетчиков (прямого счета), рассмотренных выше, существуют счетчики которые считают в обратном направлении — вычитающие.
Рассмотрим схему асинхронного вычитающего счетчика по модулю 8 (рис.13.5).
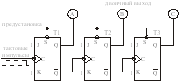
Рис.13.5. Схема асинхронного вычитающего счетчика по модулю 1
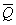
Отличие данной схемы от схемы суммирующего счетчика (рис.13.1) состоит в способе переноса сигнала от триггера к триггеру. В суммирующем счетчике синхронизирующий вход каждого триггера связан с прямым выходом Q предыдущего триггера. В вычитающем счетчике синхронизирующий вход каждого триггера связан с инверсным выходом предыдущего триггера. В счетчике изображенном на рис.13.5, перед началом счета в обратном направлении предусмотрена предварительная его установка в состояние 111 (десятичное число 7) с помощью входа предустановки (S). Счетная последовательность двоичных чисел приведена в табл.13.3.
Счетная последовательность импульсов
Вычитающий счетчик, схема которого показана на рис.13.5 — счетчик циклического типа. Когда этот счетчик приходит в состояние 000, он снова начинает счет с двоичного числа 111. В некоторых случаях нужны счетчики, которые останавливаются, когда исчерпывается вся счетная последовательность. Рассмотрим, какие изменения нужно внести в схему вычитающего счетчика, чтобы счет прекращался при достижении состояния 000.
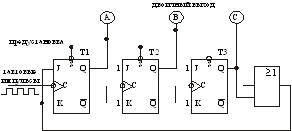
Рис.13.6. Схема самоостанавливающегося счетчика
Из рис.13.6 видно, что для этого нужно ввести в схему логический элемент ИЛИ, который будет устанавливать на входах J и K триггера T1 уровень логического 0, когда на выходах (C, B, A) счетчика появится сигнал 000. Если нужно начать новый цикл счета с двоичного числа 111, на вход предустановки S следует подать уровень логического 0.
Используя один логический элемент или их комбинацию, можно останавливать счет прямом и обратном направлении, на любом наперед заданном двоичном числе. Выход логического элемента нужно для этого присоединить к входам J и K первого триггера в асинхронном счетчике. При этом триггер T1 переводится в режим хранения.
Счетчики — делители частоты
Одной из функций которую выполняют счетчики в цифровых системах, является деление частоты. Пример простой системы с делителем частоты показан на рис.13.7. Эта система составляет основу цифровых часов. Периодический сигнал электросети с частотой 50 Гц, сформированный в виде последовательности прямоугольных импульсов, подается на вход системы, которая делит частоту на 50.

Рис.13.7. Система с делителем частоты
На выходе схемы имеем последовательность прямоугольных импульсов с частотой 1 Гц (1 импульс в 1 сек). Это таймер секунд.
На рис.13.8 схематически изображен декадный счетчик, а на рис.13.9 приведены временные диаграммы для его синхронизирующего входа C и выхода QD, соответствующего двоичному разряду восьмерок.
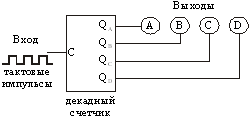
Рис.13.8. Схема декадного счетчика

Рис.13.9. Временные диаграммы декадного счетчика
Из рис.13.9 видно, что 20 импульсов на входе счетчика преобразуются в 2 выходных импульса. Выполняется деление 20/2=10. Снимая сигнал с входа QD, декадного счетчика, получим счетчик‑делитель на 10. Т.е. частота выходного сигнала состовляет 1/10 частоты на входе счетчика.
Последовательно соединяя рассмотренный декадный счетчик (счетчик‑делитель на 10) и по модулю 5 (счетчик‑делитель на 5) получим схему, осуществляющую деления частоты на 50. Структура такой схемы показана на рис.13.10. Последовательность прямоугольных импульсов с частотой 50 Гц поступает на вход счетчика — делителя на 5, а с его выхода с частотой 10 Гц подается на вход счетчика‑делителя на 10. На выходе схемы получим сигнал с частотой 1 Гц.
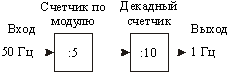
Рис.13.10. Структурная схема делителя частоты на 50
Функция деления частоты используется в таких цифровых устройствах, как частотомер, осциллограф и т.п.
Интегральные схемы счетчиков
На рис.13.11 представлена схема четырехразрядного двоичного счетчика‑делителя на 2, на 6 и на 12 (К155ИЕ4).
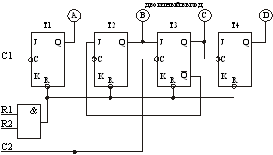
Рис.13.11. Схема четырехразрядного двоичного счетчика
Если подать тактовые импульсы с частотой f на вход С1, то на выходе А получим частоту f/2. Тактовые импульсы с частотой f на входе С2 запускают делитель на 6 и на выходе D имеем частоту f/6. При этом на выходах B и C имеем импульсы с частотой f/3. На выводы R1 и R2 подаются команды сброса. Для построения счетчика с модулем деления 12, требуется соединить делители на 1 и на 6, соединив выход А со входом С2. На вход С1 подается входная частота f, на выходе D получаем последовательность импульсов с частотой f/12.
Рассмотрим пример структурного проектирования счетчиков. Выполним синтез структуры суммирующего синхронного (параллельного) счетчика по модулю 10 на JK‑триггерах. Следует отметить, что синхронные счетчики обычно строятся на базе RS, JK, D‑триггеров, синхронизируемых фронтом.
Таблица состояний счетчика

Функция переходов показывает изменения (или сохранения) состояния разряда в зависимости от значений управляющих сигналов. Эта функция принимает следующие значения
переход из состояния Qn=0 в Qn+1=1,
переход из состояния Qn=1 в Qn+1=0,
сохранение состояния Qn=Qn+1=0,
сохранение состояния Qn=Qn+1=1.
Используя таблицу состояний счетчика (табл. 13.4) для каждого разряда представляем функцию переходов в виде карты Карно (рис. 13.12).

Рис. 13.12. Карты Карно для функции переходов
В клетках карты указываются значения функции переходов. Знаком «X» обозначаются безразличные наборы, которые соответствуют нештатным состояниям счетчика.
Определив для каждого из значений FQ соответствующие ему значения входных переменных J и K, получим словарь переходов JK‑триггера (табл. 13.5).
Словарь переходов JK-триггера
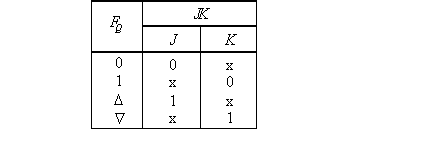
Используя словарь переходов JK‑триггера получаем карты Карно для функций входов J‑ и K‑триггеров в каждом разряде (рис. 13.13).
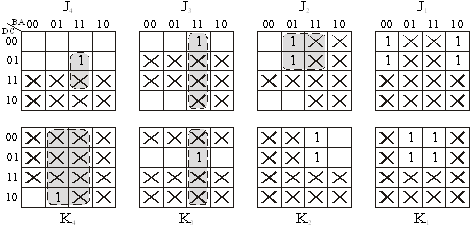
Рис. 13.13. Карты Карно для входов J и K триггеров
На основание карт Карно произведем минимизацию функции входов. В результате объединения клеток, показанных на рис. 13.13, получим простые выражения для функции входов
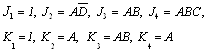
Рассмотрим более подробно минимизацию функции J4. Эта функция имеет восемь безразличных наборов, обозначенных «X» на рис. 13.13. Доопределим функцию таким образом, чтобы она имела значения J4=1 при ABCD=1111, выполним объединение клеток (рис. 13.13) и получим минимально дизъюктивную нормальную форму (МДНФ) в виде
В соответствие с полученными выражениями для функции входов построим декадный счетчик (рис. 13.14).
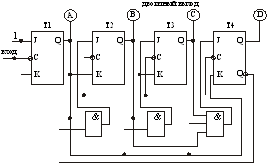
Рис. 13.14. Схема декадного счетчика
Из рис.13.14 видно, что схема декадного счетчика реализована на четырех триггерах и трех логических элементах И, два из которых имеют два входа и один имеет три входа. Счетчик, изображенный на рис. 13.14 является параллельным, т.к. все триггеры переключаются одновременно (синхронно).
Информация о работе «Общие сведения о счетчиках»
Раздел: Информатика, программирование
Количество знаков с пробелами: 15519
Количество таблиц: 0
Количество изображений: 14
Счетчики информатики
В теории вычислимости, счетчик считается типом памяти. Счетчик хранит одно натуральное число (изначально ноль ) и может быть произвольно длинным. Счетчик обычно рассматривается вместе с конечным автоматом (FSM), который может выполнять следующие операции со счетчиком:
- Проверять, равен ли счетчик нулю
- Увеличивать счетчик на единицу.
- Уменьшить счетчик на единицу (если он уже равен нулю, это оставляет его без изменений).
Следующие машины перечислены в порядке мощности, каждая из которых строго более мощная, чем одна под ним:
- Детерминированный или недетерминированный автомат плюс два счетчика
- Недетерминированный автомат плюс один стек
- Недетерминированный автомат плюс один счетчик
- Детерминированный автомат плюс один счетчик
- Детерминированный или недетерминированный конечный автомат.
Для первого и последнего не имеет значения, является ли конечный автомат детерминированным конечным автоматом или недетерминированным конечным автоматом. автомат. У них одинаковая сила. Первые два и последний являются уровнями иерархии Хомского.
Первая машина, автомат плюс два счетчика, эквивалентна по мощности машине Тьюринга. См. Статью о счетных машинах для подтверждения.
Веб-счетчик
A Веб-счетчик или счетчик посещений — это компьютерная программа, которая указывает количество посетителей или обращений, которые имеет конкретная веб-страница. получила. После настройки эти счетчики будут увеличиваться на единицу при каждом обращении к веб-странице в веб-браузере.
. Число обычно отображается в виде встроенного цифрового изображения или простого текст или на физическом счетчике, таком как механический счетчик. Изображения могут быть представлены различными шрифтами или стилями; классический пример — колеса одометра ..
веб-счетчик был популярен в середине-конце 1990-х и начале 2000-х годов, позже его заменили более подробные и полные измерения веб-трафика.
Счетчики на базе компьютеров
Многие системы автоматизации используют ПК и ноутбуки для мониторинга различных параметров машин и производственных данных. Счетчики могут подсчитывать такие параметры, как количество произведенных штук, номер партии продукции и измерения количества использованного материала.
Механические счетчики
Задолго до того, как электроника стала обычным явлением, для подсчета событий использовались механические устройства. Они известны как счетчики подсчета. Обычно они состоят из ряда дисков, установленных на оси, с цифрами от нуля до девяти, нанесенными на их края. Крайний правый диск перемещается на один шаг при каждом событии. Каждый диск, кроме самого левого, имеет выступ, который после завершения одного оборота перемещает следующий диск влево на один шаг. Такие счетчики использовались в качестве одометров для велосипедов и автомобилей и в магнитофонах, ТРК, в производственном оборудовании, а также в другом оборудовании. Одним из крупнейших производителей была компания Veeder-Root, и ее название часто использовалось для этого типа счетчиков.
Ручные счетчики используются в основном для инвентаризации и подсчета людей, посещающих События.
Электромеханические счетчики использовались для накопления итогов в вычислительных машинах, которые стали пионерами в отрасли обработки данных.
 Механические контрколеса с обеих сторон. Выступ на колесе, показанный вверху, зацепляет храповик на колесе под каждым поворотом.
Механические контрколеса с обеих сторон. Выступ на колесе, показанный вверху, зацепляет храповик на колесе под каждым поворотом. Несколько механических счетчиков.
Несколько механических счетчиков. Ранняя машина для подсчета результатов IBM с механическими счетчиками.
Ранняя машина для подсчета результатов IBM с механическими счетчиками.
Счётчики
СЧЕТЧИКИ 
 Общие сведения. Счетчик — цифровое устройство, осуществляющее счет числа появлений на входе определенного логического уровня. В дальнейшем во всех случаях, когда это не оговаривается специально, будем полагать, что счетчик производит подсчет числа содержащихся во входном сигнале переходов с уровня лог. 0 к уровню лог. 1. При импульсном представлении логических переменных уровню лог. 1 соответствует импульс, и счетчик ведет счет поступающих на вход импульсов. Числа в счетчике представляются определенными комбинациями состояний триггеров. При поступлении на вход очередного уровня лог. 1 в счетчике устанавливается новая комбинация состояний триггеров, соответствующая числу, на единицу большому предыдущего числа. Таким образом, счетчик представляет собой логическое устройство последовательностного типа, в котором новое состояние определяется предыдущим состоянием и значением логической переменной на входе. Для представления чисел в счетчике могут использоваться двоичная или десятичная системы счисления. При использовании двоичной системы состояния триггеров и соответствующие им уровни на прямых выходах триггеров определяют цифры двоичных разрядов числа. Если для регистрации двоичного числа в счетчике используется n триггеров, то максимальное значение числа, до которого может вестись счет, N = 2 n — 1. Так, при n = 4 N = l5. На рис. 8.40 показаны вход и выходы счетчика (без раскрытия схемы счетчика), а в табл. 8.19 приведено состояние триггеров, соответствующее различному числу поступивших на вход импульсов. При использовании десятичной системы счисления цифры разрядов десятичного числа в счетчике представляются в четырехразрядной двоичной форме, т. е. используется двоично-кодированная десятичная система счисления. Таким образом, для представления цифр каждого разряда десятичного числа требуется четыре триггера, и если число десятичных разрядов k, то число триггеров, необходимое для регистрации чисел в счетчике равно 4k, а максимальное значение чисел N = 10 k — 1. В табл. 8.20 показана последовательность состояний триггеров в двухразрядном десятичном счетчике, приведенном на рис. 8.41.
Общие сведения. Счетчик — цифровое устройство, осуществляющее счет числа появлений на входе определенного логического уровня. В дальнейшем во всех случаях, когда это не оговаривается специально, будем полагать, что счетчик производит подсчет числа содержащихся во входном сигнале переходов с уровня лог. 0 к уровню лог. 1. При импульсном представлении логических переменных уровню лог. 1 соответствует импульс, и счетчик ведет счет поступающих на вход импульсов. Числа в счетчике представляются определенными комбинациями состояний триггеров. При поступлении на вход очередного уровня лог. 1 в счетчике устанавливается новая комбинация состояний триггеров, соответствующая числу, на единицу большому предыдущего числа. Таким образом, счетчик представляет собой логическое устройство последовательностного типа, в котором новое состояние определяется предыдущим состоянием и значением логической переменной на входе. Для представления чисел в счетчике могут использоваться двоичная или десятичная системы счисления. При использовании двоичной системы состояния триггеров и соответствующие им уровни на прямых выходах триггеров определяют цифры двоичных разрядов числа. Если для регистрации двоичного числа в счетчике используется n триггеров, то максимальное значение числа, до которого может вестись счет, N = 2 n — 1. Так, при n = 4 N = l5. На рис. 8.40 показаны вход и выходы счетчика (без раскрытия схемы счетчика), а в табл. 8.19 приведено состояние триггеров, соответствующее различному числу поступивших на вход импульсов. При использовании десятичной системы счисления цифры разрядов десятичного числа в счетчике представляются в четырехразрядной двоичной форме, т. е. используется двоично-кодированная десятичная система счисления. Таким образом, для представления цифр каждого разряда десятичного числа требуется четыре триггера, и если число десятичных разрядов k, то число триггеров, необходимое для регистрации чисел в счетчике равно 4k, а максимальное значение чисел N = 10 k — 1. В табл. 8.20 показана последовательность состояний триггеров в двухразрядном десятичном счетчике, приведенном на рис. 8.41.
Аттестационный тест по курсу «Информатика» 88,33%
Информатика
Экзамен — верные ответы на 94,12%
Программирование и алгоритмизация
Аттестационный тест
Информатика
Информатика
Тест 1 — Основы программирования Си
Программирование и алгоритмизация
Экзамен — Теория 2023 г
Информатика
499 149 руб.
Наряду с суммирующими счетчиками, в которых в процессе счета каждое очередное число на одну единицу превышает предыдущее, используются и такие счетчики, в которых в процессе счета числа последовательно убывают (эти счетчики называются вычитающими). Находят применение счетчики, которые допускают в процессе работы автоматическое переключение (реверс) из режима суммирующего счетчика в режим вычитающего счетчика, и наоборот. Такие счетчики называют реверсивными. Хотя для построения счетчиков могут использоваться любые типы триггеров, на которых может быть организован счетный вход, в дальнейшем будем пользоваться только одним типом, JK-триггерами.
| Таблица 8.20 | ||||||||
| Число поступивших импульсов | Состояние триггеров | |||||||
| Q 2 4 | Q 2 3 | Q 2 2 | Q 2 1 | Q 1 4 | Q 1 3 | Q 1 2 | Q 1 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| . | . | . | . | . | . | . | . | . |
| 9 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| . | . | . | . | . | . | . | . | . |
| 99 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
Суммирующие двоичные счетчики. рис 8.41
рис 8.41  В суммирующем счетчике поступление на вход очередного уровня лог. 1 (очередного импульса) вызывает увеличение на одну единицу хранимого в счетчике числа. Таким образом, в счетчике устанавливается число, которое получается путем суммирования предыдущего значения с единицей. Это суммирование проводится по обычным правилам выполнения операций сложения в двоичной системе счисления. Например, Заметим, что в процессе такого суммирования имеют место следующие особенности:
В суммирующем счетчике поступление на вход очередного уровня лог. 1 (очередного импульса) вызывает увеличение на одну единицу хранимого в счетчике числа. Таким образом, в счетчике устанавливается число, которое получается путем суммирования предыдущего значения с единицей. Это суммирование проводится по обычным правилам выполнения операций сложения в двоичной системе счисления. Например, Заметим, что в процессе такого суммирования имеют место следующие особенности:
- если цифра некоторого разряда остается неизменной либо изменяется с 0 на 1, то при этом цифры более старших разрядов не изменяются;
- если цифра некоторого разряда изменяется с 1 на 0, то происходит инвертирование цифры следующего за ним более старшего разряда.
Этот принцип использован при построении схемы счетчика, представленной на рис. 8.42,а. В построении схемы имеются следующие особенности:
- входы J и K в каждом триггере объединены и на эти входы подан уровень лог. 1, таким образом, в каждом триггере синхронизирующий вход С является счетным входом триггера;
- сигнал с прямого выхода триггера каждого разряда поступает на счетный вход С триггера следующего более старшего разряда, а на счетный вход триггера 1-го разряда Тг1 подаются входные просчитываемые импульсы.

Если на счетном входе С триггера действует импульс, то его положительным фронтом переключается ведущая часть триггера, на отрицательном фронте — ведомая его часть. Итак, при каждом изменении сигнала на счетном входе с уровня лог. 1 на уровень лог. 0 изменяется на противоположное состояние выхода триггера. Таким образом, на отрицательном фронте сигнала на выходе триггера происходит переключение следующего за ним триггера более старшего разряда. На рис. 42,б показана временная диаграмма работы данного счетчика.
С каждым входным импульсом число в счетчике увеличивается на единицу. Такое нарастание числа происходит до тех пор, пока после (2 n — 1)-го входного импульса (n — число разрядов в счетчике) не установится в счетчике двоичное число 11. 1. Далее с приходом 2 n -го импульса в счетчике устанавливается исходное состояние 00 . 0, после чего счет ведется сначала. Таким образом, при непрерывной подаче на вход импульсов счетчик циклически с периодом в 2 n входных импульсов сбрасывается в исходное состояние.
Рассмотренная схема счетчика имеет следующие недостатки. Пусть первые k триггеров младших разрядов счетчика установлены в состояние лог. 1 и на вход счетчика поступает очередной импульс. При этом будет происходить процесс последовательного переключения триггеров. Если x — время переключения триггера, то относительно отрицательного фронта входного импульса первый триггер переключится с задержкой x, второй триггер переключается с задержкой x относительно отрицательного фронта сигнала на выходе первого триггера и с задержкой 2x относительно отрицательного фронта входного импульса и т. д. Следовательно, задержка в переключении k-го триггера составит kx. При большом числе разрядов задержка в переключении триггера старшего разряда может оказаться недопустимо большой. Ниже рассматриваются способы уменьшения этой задержки и, таким образом, увеличения быстродействия счетчика.
Для дальнейшего удобнее описывать процесс суммирования с помощью логических выражений.
Пусть a1, . аn — цифры разрядов числа до суммирования; cl, . сn — цифры разрядов числа, получаемого в результате суммирования с единицей; pi — значение переноса, формируемого в (i — 1)-м разряде счетчика и передаваемого в 1-й разряд.
Функционирование i-го разряда счетчика можно описать таблицей истинности (табл. 8.21).
Поступление лог. 1 на вход счетчика можно представить переносом pl = l, подаваемым на первый разряд счетчика. Из таблицы истинности следует:
- устанавливающееся в i-м разряде значение ci = ai
 i /
i /  ipi может быть получено путем подачи переноса pi на счетный вход триггера i-го разряда, хранившего значение ai,
ipi может быть получено путем подачи переноса pi на счетный вход триггера i-го разряда, хранившего значение ai, - перенос, передаваемый в (i + l)-й разряд, pi+1 = aipi. Так как p1 = 1 то р2 = a1.
Счетчики. Назначение, устройство, классификация, принцип действия, область применения. Типовые интегральные схемы счетчиков.
Счетчиком называется устройство, сигналы на выходе которого в определенном коде отображают число импульсов, поступивших на счетный вход. Счетчик, образованный цепочкой из m триггеров может подсчитать в двоичном коде 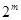 импульсов. Каждый из триггеров называется разрядом счетчика. Число
импульсов. Каждый из триггеров называется разрядом счетчика. Число 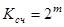 называется коэффициентом или модулем счета.
называется коэффициентом или модулем счета.
Информация может сниматься с прямых и инверсных выходов триггеров. Когда число входных импульсов 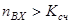 , то при n входа равном Kсч происходит переполнение, счетчик возвращается в нулевое состояние и повторяет цикл. Каждый разряд счетчика делит частоту входных импульсов пополам. Для периодических сигналов
, то при n входа равном Kсч происходит переполнение, счетчик возвращается в нулевое состояние и повторяет цикл. Каждый разряд счетчика делит частоту входных импульсов пополам. Для периодических сигналов 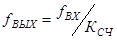 .
.
Коэффициент счета называют коэффициентом деления, следовательно каждый счетчик может использоваться как делитель частоты.
Основные параметры: емкость и быстродействие. Емкость численно равна коэффициенту счета и характеризует число импульсов, доступных счету за 1 цикл. Быстродействие определяется двумя параметрами: разрешающей способностью и временем установления.
Под разрешающей способностью подразумевают минимальное время между двумя сигналами, при которых еще не возникают сбои в работе tразр.сч.
Время установления кода tуст равно времени между моментом поступления входного сигнала и переходом счетчика в новое состояние.
Счетчики классифицируются следующим образом:
1) по модулю счета:
· с произвольным фиксированным модулем счета
· с переменным модулем
2) по направлению счета:
3) по способу организации внутренних связей
· с последовательным переносом (асинхронные)
· с параллельным переносом (синхронные)
· с комбинированным переносом
Классификационные признаки независимы и могут встречаться в разных комбинациях.
Число, записанное в счетчик, определяется по формуле:
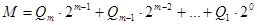
где m – номер триггера,
Q – может принимать значение «1» и «0»,
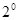
– вес младшего разряда.
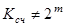
Введением дополнительных логических связей (обратных и прямых) счетчики могут быть обращены в недвоичные, для которых . Например, двоично-десятичные с Ксч=10 (двоичный по коду счета, десятичный по числу состояний). Организуется из 4-х разрядных двоичных путем исключения избыточных состояний за счет введения дополнительных связей. Когда счетчик используется в качестве делителя, направление счета роли не играет.
Счетчики с последовательным переносом представляют собой цепочку триггеров, в которых импульсы, подлежащие счету, поступают на вход 1-го триггера, а сигнал переноса передается последовательно от одного разряда к другому.
Достоинства: простота схемы и увеличение разрядности.
Недостатки: низкое быстродействие из-за последовательного принципа работы.
Счетчики с параллельным переносом.
У них счетные импульсы подаются одновременно на все тактовые входы, а каждый из триггеров цепочки служит по отношению к последующему только источником информационных сигналов. Срабатывание триггеров параллельного счетчика происходит синхронно, а задержка переключения всего счетчика равна задержке одно триггера.
В счетчике с параллельно-последовательным переносомтриггеры соединены в группы так, что отдельные группы образуют счетчики с параллельным переносом внутри группы, а группы соединяются в счетчик с последовательным переносом. Общий коэффициент счета равен произведению коэффициентов счета всех групп.
Счетчики ТТЛ с последовательным переносом
Состоят из 4-х одинаковых JK-триггеров, которые могут использоваться как по прямому назначению, так и в качестве ТК-триггеров. Переброс осуществляется по срезу. Три триггера соединяются в последовательную цепочку, 4-й самостоятельно.
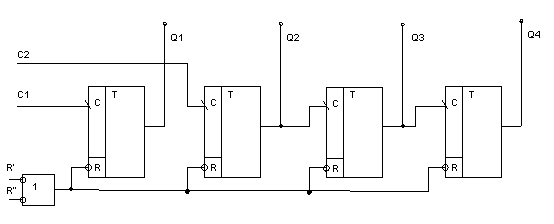
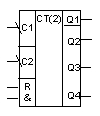

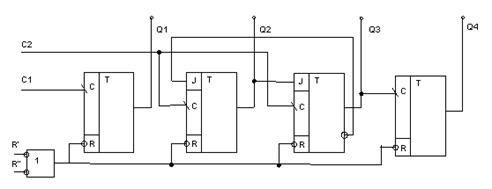
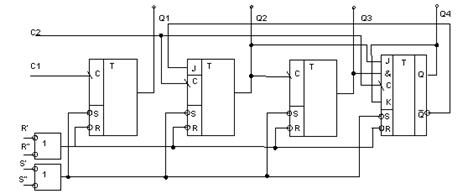
Счетчик ТТЛ с параллельным переносом
Двоично-десятичный суммирующий счетчик.
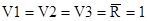
Имеет 4 входа предварительной установки счетчика при V1=0 независимо от предыдущего состояния и сигналов на входах С, V2, V3. При происходит нормальный счет, причем переброс осуществляется по переднему фронту. Счет либо от нуля, либо от информации, записанной на входы D.
При «1» на входе V3 на выходе Р формируется импульс логической «1» (перенос) с девятым входным импульсом.
V3 – разрешает перенос.
V2=0 – прерывает счет, однако информация на выходах при этом сохраняется.
V1 – предварительная запись.

Дата добавления: 2017-01-26 ; просмотров: 5458 ;
Счетчики
Рисунок 6.9 — а) схема асинхронного счетчика с последовательным переносом на Т-триггерах; б) диаграмма работы счетчика; в) обозначение асинхронного последовательного счетчика на принципиальных схемах.
Количество импульсов, которое может подсчитать счетчик, определяется из выражения N = 2 П — 1, где п — число триггеров, а так как в цифровой технике за начало отсчета принимается 0, то из выражения вычитается единица. На рисунке 6.9, а представлена схема асинхронного счетчика с последовательным переносом на Т-триггерах.
Счетчики бывают суммирующие, когда счет идет на увеличение, и вычитающие, если счет идет на уменьшение. Операцию, когда счетчик может переключаться в процессе работы с суммирования на вычитание и наоборот, называют реверсом, а счетчик — реверсивным.
Кроме этого счетчики подразделяются на синхронные и асинхронные. У синхронных счетчиков все разрядные триггеры синхронизируются параллельно одними и теми же синхроимпульсами. Асинхронные же счетчики имеют последовательную синхронизацию, т.е. каждый последующий разрядный триггер синхронизируется выходными импульсами триггера предыдущего разряда (рисунок 6.9,а). Асинхронные счетчики часто называют
последовательными, а синхронные счетчики — параллельными.
Рассмотренные выше ИМС счетчиков, регистров и триггеров называют схемами последовательностного типа, далее будут рассмотрены ИМС комбинационного типа.
Шифраторы и дешифраторы
Шифратор это функциональный узел, осуществляющий преобразование сигнала, поступающего на его вход, в код на его выходе. Чаще всего шифратор, осуществляет преобразование позиционного кода в двоичный (в позиционном коде число определяется той позицией, какую занимает во входящем ряду, представляющий его элемент).

Рисунок 6.10 — а) схема шифратора на элементах ИЛИ; б) таблица состояний шифратора.
На рисунке 6.10,а представлен пример схемы шифратора, отличительной особенностью которого является то, что разряд цифры 1 не задействован, так как согласно таблице состояний (рисунок 6.10, б), ей соответствует код 000.
Дешифратор (показан на рисунке 6.11,6) выполняет преобразование противоположное шифратору, т.е. преобразует двоичный код в позиционный. Так же существуют специальные типы дешифраторов, которые осуществляют, например, перевод двоичных чисел в код многосегментного индикатора.

Рисунок 6.11 — а) обозначение шифратора на принципиальных схемах; б) обозначение дешифратора на принципиальных схемах.
Схемотехническая реализация элементов вычислительной техники
Счетчиком называется электронная схема, предназначенная для подсчета числа сигналов, поступающих на его счетный вход . Счетчики используются в устройстве управления компьютера при построении распределителей импульсов и организации циклов, в счетчиках команд для формирования адреса выполняемой команды при естественном порядке выполнения и в некоторых других устройствах ЭВМ. Также счетчики широко применяются в качестве самостоятельных узлов в различных системах цифровой автоматики.
Суть работы счетчика заключается в изменении на единицу зафиксированного в нем значения с приходом каждого счетного сигнала. Счетчики принято подразделять на суммирующие, вычитающие и реверсивные. Суммирующие счетчики увеличивают свое значение , вычитающие – уменьшают, а реверсивные могут работать как на прибавление, так и на вычитание в зависимости от сигналов управления. Параметром, определяющим информационную емкость счетчика, является модуль пересчета, равный числу внутренних состояний. Это значение проставляется на УГО после аббревиатуры CT (Рис. 5.12).
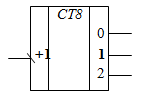
Рис. 5.12. Условно-графическое обозначение трехразрядного суммирующего счетчика
Пример построения асинхронного трехразрядного двоичного суммирующего счетчика приведен на Рис. 5.13.
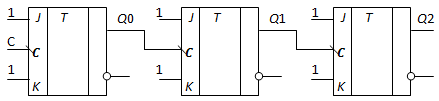
Рис. 5.13. Схема асинхронного трехразрядного счетчика
Для построения этого счетчика использованы JK-триггеры с динамической синхронизацией по спаду синхросигнала. Каждый JK- триггер в счетчике включен в режим инвертирования своего состояния при переключении синхросигнала с высокого уровня на низкий (см. Табл. 5.10). Идеализированная временная диаграмма работы этого счетчика показана на Рис. 5.14.
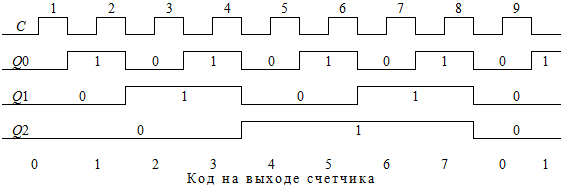
Рис. 5.14. Временная диаграмма работы счетчика
С увеличением разрядности асинхронного счетчика увеличивается его задержка и, следовательно, уменьшается быстродействие . В том числе и поэтому, реальные микросхемы счетчиков строятся на основе синхронных триггерных схем.
Обычно счетчик имеет вход установки в нулевое состояние (асинхронный сброс составляющих его триггеров в «0»). Некоторые счетчики имеют цепи установки в произвольное начальное состояние, с которого уже будет начинаться операция счета.

 Механические контрколеса с обеих сторон. Выступ на колесе, показанный вверху, зацепляет храповик на колесе под каждым поворотом.
Механические контрколеса с обеих сторон. Выступ на колесе, показанный вверху, зацепляет храповик на колесе под каждым поворотом. Несколько механических счетчиков.
Несколько механических счетчиков. Ранняя машина для подсчета результатов IBM с механическими счетчиками.
Ранняя машина для подсчета результатов IBM с механическими счетчиками. i /
i /  ipi может быть получено путем подачи переноса pi на счетный вход триггера i-го разряда, хранившего значение ai,
ipi может быть получено путем подачи переноса pi на счетный вход триггера i-го разряда, хранившего значение ai,


