Rms напряжение что это

Содержание

Морские волны подобны синусоидальной волне переменного напряжения, которая используется в качестве эталонной при при определении качества питания. Отклонения от чисто синусоидальной формы волны могут быть обусловлены гармоническими составляющими, некратными гармониками, а также импульсными или колебательными переходными процессами. Изменения амплитуды синусоидального сигнала можно классифицировать следующим образом: падения, всплески и продолжительное перенапряжение либо пониженное напряжение. В то время как изменения в частоте питающего напряжения сравнительно редки и возникают при серьезных неполадках оборудования, чаще имеет место сдвиг фаз при провалах и всплесках. Для того чтобы охарактеризовать или описать синусоидальный сигнал, находящийся под воздействием описанных факторов, влияющих на качество электроэнергии, используются измерения истинных среднеквадратичных значений (Root Mean Squared — RMS). Являющиеся полезными во многих ситуациях, в ряде случаев такие измерения могут оказаться неадекватными либо вводить в заблуждение.

Что же представляют собой RMS? Среднеквадратичные значения получаются в результате математической процедуры, используемой для расчета единичного значения по последовательности отсчетов. Это позволяет сравнивать один цикл с другим, или одну фазу с другой. RMS-напряжение является эффективным значением изменяющегося или переменного напряжения. Это значение должно соответствовать такой же мощности, как и в случае постоянного напряжения, приложенного к чистому сопротивлению. В нынешнем мире дискретных волновых сигналов, вырабатываемых кристаллами процессоров цифровой обработки сигнала (ЦОС), такие измерения являются одними из наиболее легко реализуемых. Каждое значение данных в течение предопределенного периода (обычно это один цикл) умножается само на себя (возведение в квадрат), а затем все такие значения в течение периода усредняются (суммируются с последующим делением на общее количество) и из полученного значения извлекается квадратный корень.

Для стабильного постоянного сигнала каждый отсчет имеет одно и то же значение, следовательно, любой из них может служить эквивалентом RMS-значения. В случае же синусоидальной волны значения нарастают в пределах первой четверти цикла, затем уменьшаются до нуля и переходят в область отрицательных значений вплоть до минимального значения в пределах второй четверти цикла (см. рис. 1).

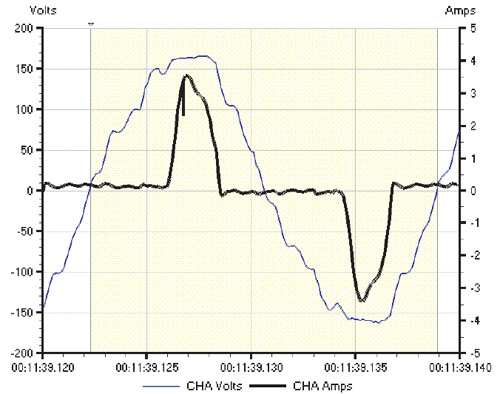
Рисунок 1. Форма волны на нагрузке однофазного источника питания с полноволновым измерителем.

RMS-значение чистого синусоидального сигнала составляет примерно 70,7% пикового значения. При искаженной форме волны это не верно, что является ответом на вопрос, почему приборы, измеряющие не в терминах истинных среднеквадратичных значений, могут выдавать совершенно различные результаты при различных степенях искажений и, следовательно, не могут использоваться при наличии гармоник. Те приборы, которые лишь вычисляют 71% от пикового значения будут давать неверный результат для формы тока, показанного на рис. 1. На рисунке изображена классическая форма токового сигнала однофазного источника питания с выпрямлением полной волны, присутствующего во многих электронных устройствах. Эта форма волны с гармоническими искажениями (THD) на уровне 108% имела пиковое значение 3,6 А и истинное среднеквадратичное значение 1,4 А, что не совпадает с рассчитанной величиной 0,707*3,6=2,55 А.

Действующее, среднеквадратичное, RMS, эффективное напряжение или ток, на наглядном примере.

Невысокого качества анализаторы электроэнергии, которые настроены на RMS-значения, могут пропускать некоторые данные. Ряд приборов рассчитывают RMS-значения в ходе нескольких циклов. Весьмавероятно, что эти мониторы не зафиксируют многофазовый провал в течение одного цикла, изображенный на рис. 2.

Рисунок 2. Провал в течение одного цикла в двух фазах.

Такое искажение сигнала типично для случая, когда неполадка устраняется с помощью защитного предохранителя. На рис. 3 провал в течение одного цикла, возникший вследствие пробоя при пиковом напряжении (возможно из-за неисправности изоляции или удара молнии) будет давать различные RMS-значения на каждом из трех циклов.

Рисунок 3. Однофазный провал при пробое пиковым напряжением.

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже простым графиком не отделаешься. Среднеквадратичное значение — это значение постоянного напряжения, который, проходя через нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение обозначается так: RMS (rms) — root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды Ka:

Вот некоторые значения коэффициента амплитуды Ka для некоторых сигналов переменного напряжения:

Более точные значения 1,41 и 1,73 — это √2 и √3 соответственно.

Что такое RMS?

RMS означает «Среднеквадратичный квадрат», который является математической формулой, которая внутренне вычисляется инструментами, способными использовать RMS значение для проведения измерений. Эта формула упрощена прибором для учета только положительного пика синусоиды:

Математическая формула, применяемая RMS мультиметром

Среднеквадратичное измерение надежно, когда синусоидальная волна идеальна, потому что это измерение учитывает только пиковое значение формы волны.

Итак, что происходит, когда синусоида не идеальна? Это значит, что происходит в РЕАЛЬНОМ мире?

Что такое True RMS? Это самое надежное измерение

RMS измерения нельзя считать надежными, потому что в настоящее время в любой установке имеется множество источников шума, из-за которых форма волны переменного тока никогда не бывает идеальной.

В измерении True RMS (истинное среднеквадратичное значение) используются более сложные математические формулы, которые позволяют приблизить значение к реальности, чем RMS. В дополнение к пиковым значениям они берут несколько выборок значений по каждому циклу.

Математическая формула, применяемая мультиметром True RMS

Идеальная синусоида (слева) и волна ближе к реальности (справа) под воздействием шума

Весь этот шум вызван приводами, переменными переключателями, приборами, компьютерами, дешевыми блоками питания маршрутизаторов, зарядных устройств и т. д

По этой причине, поскольку синусоидальная волна никогда не бывает совершенной, надежные измерения в установках переменного тока — это только измерения, выполненные мультиметрами True RMS.

Энергия и мощность

Уравнение (3) показывает, что результатом произведения мгновенного напряжения и тока является мгновенная мощность . Если просуммировать мгновенную мощность, умноженную на бесконечно малое время , то результатом будет энергия. Так как :

(7)

Действительно, энергия есть мощность, умноженная на время: , и энергетические пакеты можно всегда сложить для расчета полной энергии.

В качестве примера, опять возьмем последовательное соединение катушки индуктивности и резистора. На рисунке ниже черной линией показана динамика энергии во времени, рассчитанная в соответствии с уравнением (7).

Кривая мощности в случае напряжения и тока переменной полярности, также имеет периодическое изменение амплитуды с удвоенной частотой. Поскольку энергия рассеивается на сопротивлении, область серого цвета положительных значений кривой мощности больше, чем отрицательной области.

Значение энергии (черная линия) в любой момент времени равно площади под кривой мощности до этого момента. Хорошо видно, что энергия периодически возрастает сильнее, чем падает в результате амплитудной асимметрии кривой мощности относительно оси .

На рисунке показан период времени . Энергия внутри этого временного интервала , которая поступила в систему обозначена и вычисляется следующим образом:

(8)

Средняя мощность за определенный период времени равна общему количеству энергии, за это время, деленному на время измерений:

(9)

Если это подставить в уравнение (8), среднюю мощность можно вычислить для любой формы сигнала.

(10)

Это уравнение получено в соответствии с (4). Активная мощность всегда является средней мощностью.

Это уравнение для расчета средней рассеиваемой мощности всегда справедливо, потому что расчет основан на мгновенных значениях. Не имеет значения, является ток постоянным или переменным, как выглядит форма напряжения и тока и есть ли сдвиг фаз между напряжением и током.

Уравнение для расчета средней мощности лежит в основе метода, применяемого в измерителях мощности. Счетчики электроэнергии дома и на предприятиях работают в соответствии с уравнением (8), которое можно переписать в виде:

(11)

Верхний предел в интеграле — момент времени, в который счетчик энергии считывает значение.

Эффективные (RMS) значения

Среднеквадратическим (RMS), или эффективным значением является значение напряжения или тока, при котором на нагрузке рассеивается та же мощность, что и при постоянном напряжении или токе.
При переменном напряжении с эффективным значением 230В будет выделяться такое же количество тепла на нагрузке, как и при постоянном напряжении 230В. Действующее значение относится только к выделению тепла на резистивной нагрузке. Для примера, значение RMS тока полезно для измерения напряжения под нагрузкой в проводе (= резистивная), но не для измерения зарядного тока батареи или конденсатора (= поток электронов).

Среднеквадратическое значение

RMS является аббревиатурой от Root Mean Square, что буквально переводится как среднеквадратическое значение.

Над напряжением или током, как функциями времени, для вычисления значения RMS последовательно проводятся три математические операции: возведение в квадрат, усреднение и извлечение квадратного корня. Почему так?

Мощность, выделяемая на резисторе, подключенным к источнику напряжения:

(12)

Для мгновенных мощности и напряжения:

(13)

Вычисление средней мощности как функции времени показано в (10). можем подстваить из (13):

(14)

Так как — константа, то ее можно вынести за интеграл:

$begin{equation*}P_{cp}=frac{1}{T cdot R} intlimits_0^T v(t)^2 dtend{equation*}$

(15)

Перенеся напряжение в уравнении (12) в левую часть, мы можем расчитать напряжение по средней мощности и сопротивлению:

(16)

Затем, вычисленную среднюю мощность из (15), подставим в уравнение (16):

$begin{equation*}V_{RMS}=sqrt{frac{1 cdot R}{T cdot R}intlimits_0^T v(t)^2 dt}end{equation*}$

(17)

Сократив значения сопротивлений , получим:

$begin{equation*}V_{RMS}=sqrt{frac{1}{T}intlimits_0^T v(t)^2 dt}end{equation*}$

(18)

Хорошо видно, что это уравнение состоит из трех частей: квадрата , среднего и квадратного корня.

В приведенных выше выкладках вычислялось значение напряжения на резисторе. Аналогично можно сделать и для тока через резистор:

$begin{equation*}I_{RMS}=sqrt{frac{1}{T}intlimits_0^T i(t)^2 dt}end{equation*}$

(19)

Большинство мультиметров не может вычислить эффективное значение измеряемого напряжения. Чтобы узнать среднеквадратическое значение, обычно необходим специальный прибор.

На рисунке ниже показано, как вычисляет измеряемое напряжение прибор True RMS (истинные среднеквадратические значения). True RMS прибор, на практике, использует несколько иной метод работы, в котором необходим только один умножитель. Аналоговые умножители должны иметь очень низкий температурный дрейф и смещение, что делает эти инструменты достаточно дорогими.

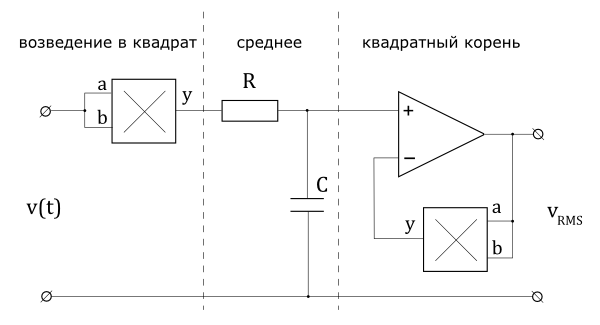
Кроме того, можно сделать расчет RMS программным путем с последовательных цифровых значений измеряемых напряжений. Этот подход обычно используется в мультиметрах и цифровых осциллографах.

Маркировка True RMS на импортных измерительных приборах

27.08.12 9:57

Маркировка True RMS на импортных измерительных приборах инженер М.Б. БеловЗАО «ТЕККНОУ» На импортных средствах измерений можно встреть аббревиатуру «True RMS» или «TRMS». Причем в анонсах на прибор отмечается, что это является явным преимуществом в точности измерений реальных значений таких электрических величин, как напряжение и силы тока. Так что же означает эта сокращенная запись, какой ее физический смысл и в каких случаях вычисление этого параметра с помощью соответствующего измерительного прибора дает преимущества при проведении измерений? Попробуем разобраться в этом вопросе, не перегружая читателя математическими выкладками. Словосочетание «True RMS» — (True Root Mean Square) – дословный перевод — среднеквадратическое из мгновенных значений переменного тока или напряжения за период или за время измерений. Это означает, что прибор в процессе измерений предварительно преобразует входной периодический сигнал в постоянный (в виде постоянного тока или напряжения). При этом реализуется математический метод среднеквадратических преобразований. Основной принцип измерений переменного напряжения или силы тока в цифровых прибора реализуется на предварительном преобразовании переменного сигнала в постоянный, как представлено на рис.1. После блока аналого-цифрового преобразователя (АЦП) уровень аналогового выходного сигнала измеряется и индицируется на цифровом дисплее, как в приборе постоянного тока. От метода преобразований зависят и формы представления значений напряжений переменного тока:

Среднеквадратическое значение (оно же действительное, эффективное или True RMS).
Средневыпрямленное значение (Mean: average rectified).
Амплитудное значение (оно же пиковое, максимальное).

Шкалы или дисплеи цифровых вольтметров и амперметров переменного тока (кроме импульсных вольтметров) всегда градуируют в среднеквадратических значениях сигнала синусоидальной формы.

Импульсные (амплитудные, максимальные, пиковые) вольтметры градуируют в амплитудных значениях синусоидального сигнала. Функция импульсных измерений (ПИК, МАХ) может также включаться в состав комбинированных приборов – портативных мультиметров.

В практических измерениях напряжения и силы тока промышленной электросети 50 Гц (или специальной сети 400 Гц) применяются цифровые вольтметры и амперметры с преобразователями, реализующие методы среднеквадратических или средневыпрямленных преобразований. Амплитудные (пиковые) преобразователи используются для фиксации значений амплитуды выбросов, скачков напряжения или максимального напряжения за наблюдаемый интервал времени в процессе измерений.

Рассмотрим подробнее три основных типа преобразователей

1. Среднеквадратический (True RMS) — самый совершенный и дорогостоящий метод. Выходное напряжение преобразователя пропорционально среднеквадратическому (действующему, эффективному) значению измеренного напряжения (Uск, Urms). Осуществляется на основе термоэлектрических, диодных, транзисторных или оптронных преобразователей.

В этом случае на активной нагрузке численно равные значения постоянного и переменного тока совершают одинаковую работу.

Для понимания физического смысла измерений напряжения переменного тока в среднеквадратических значениях приведем простой пример: на нагревательном элементе за одинаковый интервал времени должно выделиться одинаковое количество теплоты, если запитать его от сети 220 В 50 Гц, или от сети 220 В пост. тока.

Кроме того, особенностью математического преобразования данного метода является то, что теоретически, он не зависит от формы периодического сигнала на входе преобразователя. Будь-то идеальная синусоидальная форма или сигнал с большими нелинейными искажениями, прямоугольная, треугольная, произвольная и т. п. – не имеет значения. В любом случае совершаемая работа численно равных по величине постоянного и переменного сигналов будет одинаковая.

В практических измерениях из-за ограниченных свойств элементной базы степень отличия от синусоидальной формы ограничивается коэффициентом амплитуды и максимальным значением напряжения на входе прибора. Допускаемый коэффициент амплитуды обязательно указывается в сопроводительной документации на измерительный прибор.

Недостатки

Низкая чувствительность (нижний предел, как правило, не ниже 1 В).
Большая инерционность, влияющая на быстродействие измерений.
Квадратичное построение числовой шкалы.
Низкая электрическая прочность.
Повышенная стоимость прибора.

Для устранения этих недостатков используются входные усилители, специальные методы линеаризации шкалы, отрицательную обратную связь и др., что приводит к удорожанию прибора.

Преимущества

Повышенная достоверность измерений.
Погрешность измерений не зависит от нелинейных искажений и формы сигнала.

Показания значений переменного тока и напряжения полностью эквивалентны постоянному, численно равны и не требуют внесения дополнительных коэффициентов преобразования.

Рекомендации по применению

Маркировка True RMS

— самый совершенный и дорогостоящий метод. Выходное напряжение преобразователя пропорционально среднеквадратическому (действующему, эффективному) значению измеренного напряжения (Uск, Urms). Осуществляется на основе термоэлектрических, диодных, транзисторных или оптронных преобразователей.

Недостатки

Преимущества

Средневыпрямленный (Mean: average rectified)

– дешевый метод в практической реализации.

Выходное напряжение преобразователя пропорционально среднему значению выпрямленного напряжения Uсв. Осуществляется на основе выпрямительного диода или моста. По методу математических преобразований выходной уровень постоянного сигнала у такого преобразователя будет всегда ниже, чем у среднеквадратического примерно в 0,9 раз (для двух полупериодного моста):

Причем выражение (1) справедливо только в том случае если на вход преобразователя подается сигнал строго синусоидальной формы.

Для того, что бы показания такого прибора соответствовали действительным значениям (True RMS), показания средневыпрямленных значений шкалы или цифрового дисплея «принудительно подтягивают» до среднеквадратических, путем механической переградуировки рисованной шкалы или введением дополнительного коэффициента умножения для цифрового дисплея.

В итоге получается, что в приборе установлен преобразователь средневыпрямленных значений, но по табло прибора мы отсчитываем среднеквадратические (True RMS) показания. Такие вольтметры и амперметры применяются только для измерений в цепях переменного тока, о чем должно указываться в сопроводительной документации на эти приборы. Такие приборы непригодны для проведения измерений переменных напряжений и токов с несинусоидальной формойсигнала.

В специальной литературе можно найти известные зависимости напряжений между различными видами преобразователей и сделать пересчет по заранее известной форме исследуемого сигнала. Эти случаи очень редки и, как правило, на практике этим никто не занимается. Для этого существуют универсальные осциллографы, где все можно увидеть визуально, а с помощью встроенного вычислителя получить значения сразу всех форм переменного напряжения.

Показания средневыпрямленных значений также зависят от коэффициента нелинейных искажений входного сигнала, которые выражаются в увеличении погрешности измерений. Чем больше нелинейные искажения, тем больше форма периодического сигнала уходит от синусоидальной и тем больше погрешность измерений.

В технической литературе подробно не рассматривается зависимость погрешности измерений от коэффициента нелинейных искажений. Можно только привести несколько выдержек из технических описаний цифровых вольтметров, где по переменному току указывается предел допускаемых нелинейных искажений, при котором предел допускаемой погрешности измерений еще не превышает нормированные значения.

По величине этих показателей можно получить представление о степени влияния нелинейных искажений на погрешность измерений в диапазоне частот 50…1000 Гц:

Из приведенной таблицы видно, что для перечисленных моделей цифровых вольтметров ограничения по нелинейным искажениям достаточно жесткие. Нетрудно продолжить аналогию и сделать осторожный вывод, что для современных портативных мультиметров эти показатели вряд ли будут значительно лучше.

Принятые решения в схемотехнике преобразователей и их свойства давно изучены и известны, пускай они и выполнены на современной элементной базе. Согласно ГОСТ 13109-97, нормально допустимое значение коэффициента искажения синусоидальности кривой напряжения для сетей напряжения 0,38 кВ составляет 8 %, а предельно допустимое значение составляет 12 %.

Отсюда следует вывод, что такие приборы не должны применяться для достоверных измерений переменного сетевого напряжения или силы тока с документированием результатов измерений и оценки их точности. Например, нельзя оперировать показаниями прибора о ненадлежащем качестве электроэнергии по величине напряжения в сети, т.к. прибор в этом случае будет считаться ненормированным по погрешности измерений.

Тем не менее, эти приборы отличаются более низкой рыночной ценой и вполне пригодны для повседневных рутинных работ по техническому обслуживанию электрооборудования, электроустановок, а также по поиску в них неисправностей и восстановлению. Здесь не требуется измерения с оценкой точности. Дорогие приборы для этих целей приобретать нецелесообразно. Тем более, что для технических эксплуатационных служб такие «рабочие лошадки» необходимы далеко не в единичных экземплярах — практически каждому наладчику и мастеру.

Так, что вольтметры и амперметры со средневыпрямленными значениями также занимают свою достойную нишу.

Недостатки

По переменному току пригодны для измерений напряжения или силы тока только синусоидальной формы.

Зависимость точности измерений от уровня нелинейных искажений измеряемого переменного напряжения или силы тока.

Ориентировочно можно считать, что нормированная точность измерений сохраняется, если общий коэффициент нелинейных искажений измеряемого сигнала, выраженный в процентах, численно не превышает класса точности прибора.

Пик-коэффициент

Ещё одним показателем качества источника питания, часто используемым для описания периодической временно́й функции напряжения (тока), является пик-коэффициент, или пик-фактор (Crest Factor – CF). Это показатель, характеризующий способность источника питания питать нелинейную нагрузку, потребляющую импульсный ток. Пик-коэффициент для конкретной формы волны определяется как пиковое значение, делённое на среднеквадратическое значение:

Для ранее приведённых типовых случаев RMS можно вычислить и CF:

Чистая синусоида: CF=√2
Меандр: CF = 1.
Несимметричная периодическая импульсная волна со спадами D: CF=1/√D
Симметричная периодическая треугольная волна: CF=√3
Выпрямленная двухполупериодным выпрямителем синусоида: CF=√2
Выпрямленная однополупериодным выпрямителем синусоида: CF=2.

Для рис. 2 получаем:
кривая 1: CF = 1,62;
кривая 2: CF = 1,24.

Измерительные устройства Dataforth RMS

Итак, для качественных измерений среднеквадратических значений требуются измерительные приборы, которые точно реализуют уравнение среднеквадратического значения. Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение для сигналов низкого уровня, что позволяет им поддерживать измерения при высоких значениях пик-коэффициентов. Компания Dataforth разработала два продукта, удовлетворяющих этим требованиям, – True RMS-модули ввода SCM5B33 (рис. 3) и DSCA33 (рис. 4). Оба этих продукта обеспечивают гальваническую изоляцию 1500 В между входом и выходом. SCM5B33 – это съёмный панельный модуль, а DSCA33 – устройство, предназначенное для монтажа на DIN-рейку. Каждый из них обеспечивает один канал входа переменного тока, значение которого преобразуется в истинное среднеквадратическое значение постоянного тока, фильтруется, гальванически развязывается, усиливается и преобразуется в выходной сигнал напряжения или тока.

Модуль SCM5B33

Модуль ввода SCM5B33 True RMS (рис. 5) обеспечивает один канал входа переменного тока, который преобразуется в стандартное выходное напряжение или ток процесса.

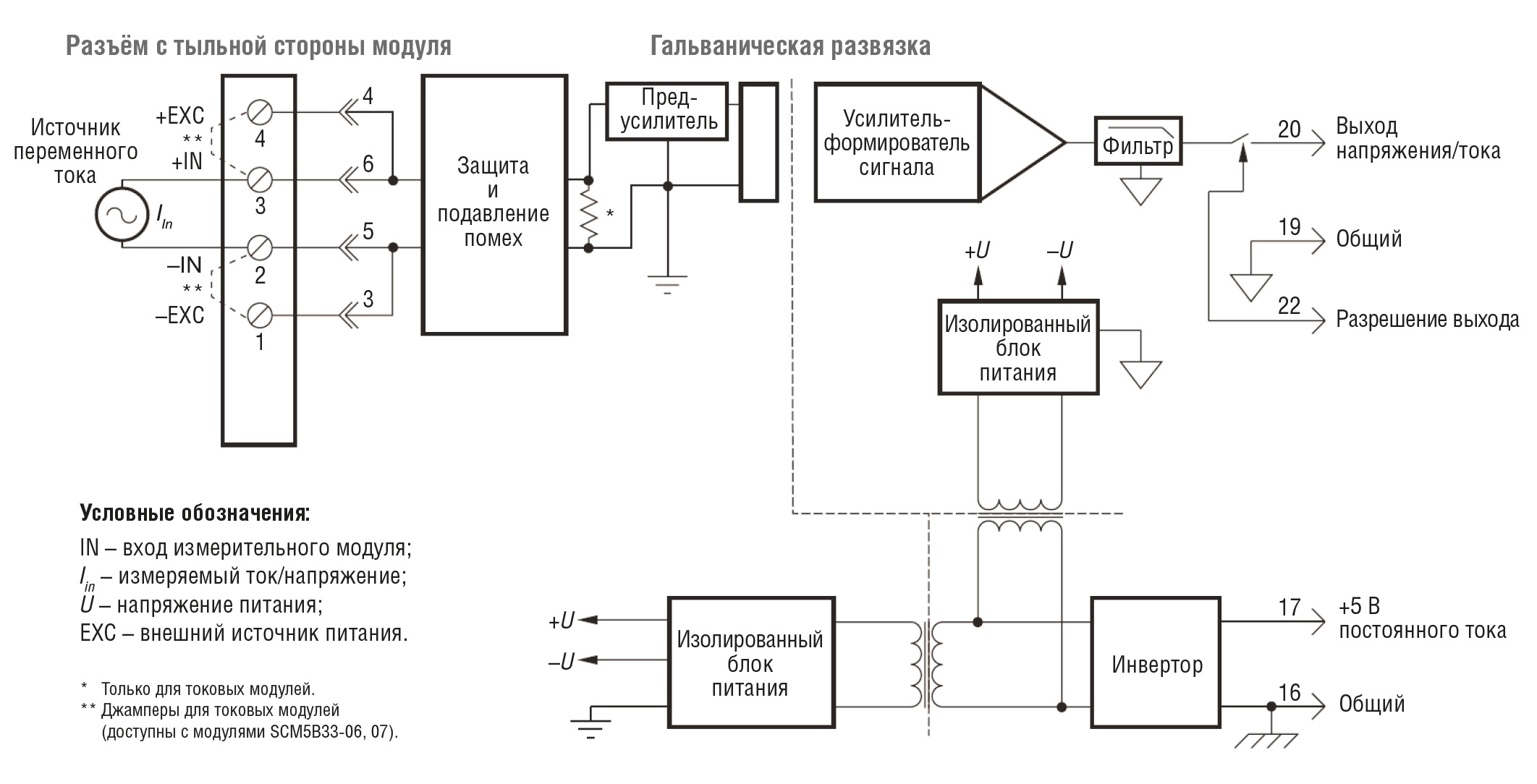
Модули SCM5B содержат полностью изолированную со стороны компьютера цепь, на которую может быть подано до ±50 В относительно общего провода (контакт 16). Эта полная изоляция означает, что для правильной работы выхода не требуется никакого соединения между общим входом/выходом и общим питанием. При желании выход модуля можно сделать включённым постоянно, просто подключив контакт разрешения чтения 22 к общему проводу ввода/вывода (контакт 19).

Входной сигнал напряжения или тока с полевой стороны обрабатывается предварительным усилителем и преобразователем среднеквадратических значений на полевой стороне изолирующего барьера. Преобразованный в постоянный ток сигнал затем гальванически развязывается запатентованной схемой и передаётся через трансформаторный изолирующий барьер, подавляющий передачу синфазных пиков и выбросов. Схема на стороне компьютера восстанавливает сигнал и преобразует его к стандартному выходному уровню. Модули питаются от +5 В постоянного тока ±5%.

Для моделей с токовым выходом требуется внешний источник питания с согласованным напряжением от 14 до 48 В постоянного тока. Подключение с последовательной нагрузкой осуществляется между контактом 20 (+) и контактом 19 (–).

Основные характеристики модуля

Измерение напряжения RMS (0…300 В) или тока (0…5 А).
Предназначен для стандартной работы с частотами от 45 до 1000 Гц (расширенный диапазон до 20 кГц).
Совместим со стандартными трансформаторами тока и потенциальными трансформаторами.
Отраслевые стандарты выхода: 0. 1, 0. 20, 4. 20 мА, 0. 5 или 0. 10 В постоянного тока.
Точность ±0,25%, калибруется на производстве.
Гальваническая изоляция на основе трансформатора 1500 В (среднеквадратическое значение).
Защита от перегрузки по входу до 480 В макс. (пиковый и постоянный ток) или 10 А RMS непрерывно.
Сертификаты ANSI/IEEE C37.90.1-1989, CSA, FM.

Модуль DSCA33

Модуль ввода DSCA33 True RMS (рис. 6) по всем основным характеристикам идентичен SCM5B33. Отличие состоит в его конструктиве, оптимизированном для размещения на DIN-рейке.

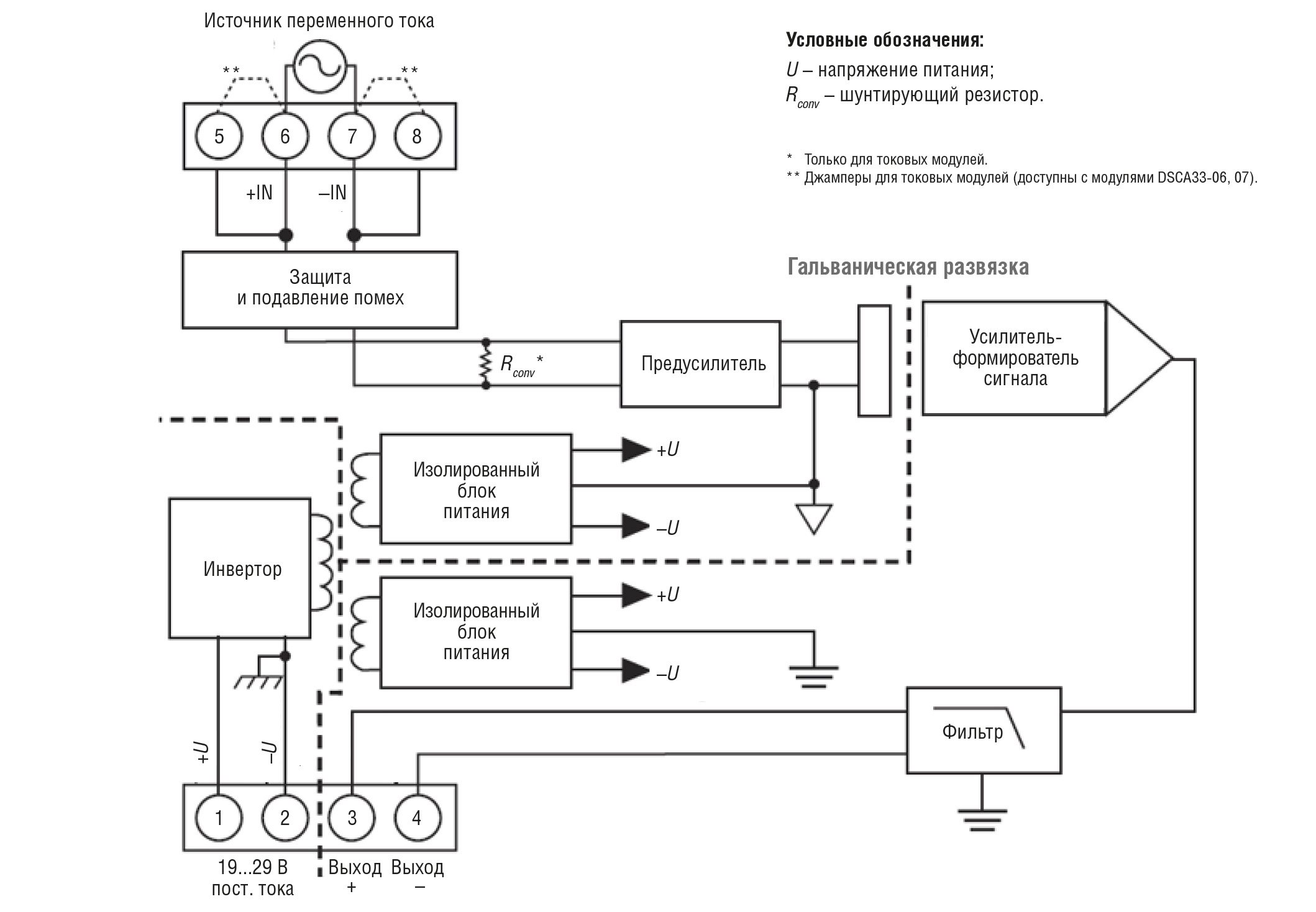
Модули DSCA33 обладают превосходной стабильностью во времени и не требуют повторной калибровки, однако в ситуациях, когда необходима точная настройка, это можно сделать вручную. Регулировки выполняются с помощью потенциометров, расположенных под этикеткой на передней панели, и не являются интерактивными.