Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используются параллельное и последовательное соединения.
1. Параллельное соединение конденсаторов (применяется для увеличения емкости). У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна ( ) (рис. 5.5).
Если емкости отдельных конденсаторов , то их заряды:
Полная емкость батареи:
Вывод: при параллельном соединении конденсаторов полная емкость батареи равна сумме емкостей отдельных конденсаторов.
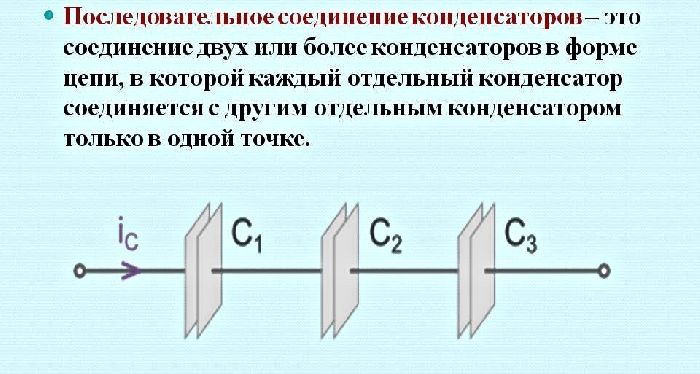
2. Последовательное соединение конденсаторов (применяется для уменьшения емкости) (рис. 5.6)
У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи равна
где для любого конденсатора:
С другой стороны,
Вывод: при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Результирующая емкость всегда меньше наименьшей емкости, используемой в батарее.
6. Энергия заряженного проводника и заряженного конденсатора. Энергия электростатического поля
Энергия двух неподвижных точечных зарядов. Работа электростатических сил не зависит от траектории перемещения заряда. Следовательно – электростатические силы консервативны, а электростатическое поле – потенциально. Значит, система зарядов обладает потенциальной энергией. Рассмотрим два неподвижных точечных заряда и , находящихся на расстоянии r друг от друга. Каждый заряд, в поле другого заряда, обладает потенциальной энергией:
где и , соответственно, потенциалы, создаваемые зарядом в точке нахождения заряда и зарядом в точке нахождения заряда .
То есть, энергия двух неподвижных точечных зарядов:
Энергия системы неподвижных точечных зарядов:
где – потенциал, создаваемый в той точке, где находится заряд , всеми зарядами, кроме i-го.
Энергия заряженного уединенного проводника. Рассмотрим работу, совершаемую при увеличении потенциала проводника от 0 до φ. Для увеличения заряда уединенного проводника (заряд Q, емкость С, потенциал φ) на dQ необходимо совершить элементарную работу
dA = φdQ = φd(Cφ) = Cφdφ;
т.е. энергия заряженного уединенного проводника равна работе, которую необходимо совершить, чтобы зарядить этот проводник
Энергия заряженного конденсатора:
где Q – заряд конденсатора, С – емкость конденсатора, Δφ – разность потенциалов между обкладками конденсатора.
Энергия электростатического поля. В формулу (20) для энергии плоского конденсатора подставим и Δφ = Еd, тогда получаем выражение для энергии электростатического поля:
Объемная плотность энергии электростатического поля – это энергия единицы объема этого поля:
Эта формула справедлива только для изотропного диэлектрика (выполняется соотношение Р = æ ).
Полученные формулы связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает вопрос: где локализована энергия и что является ее носителем – заряды или поле? Электростатика изучает постоянные во времени поля неподвижных зарядов, т.е. в ней поля и обусловившие их заряды неотделимы друг от друга, поэтому электростатика ответить на поставленный вопрос не может. Переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяться в пространстве в виде электромагнитных волн, способных переносить энергию. Это подтверждает основное положение теории близкодействия о том, что энергия локализована в поле и что носителем энергии является поле.
Последовательное и параллельное соединение конденсаторов. Схемы и расчёты для конденсаторов
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
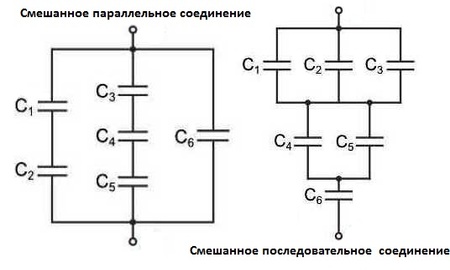
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
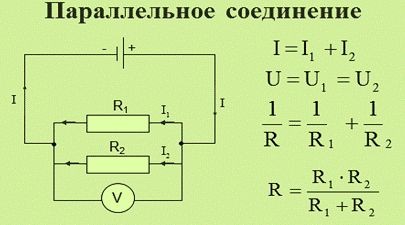
Падение напряжения при параллельном соединении
Смешанное подключение
Но, стоит учитывать, что для соединения различных конденсаторов необходимо учитывать напряжение сети. Для каждого полупроводника этот показатель будет отличаться в зависимости от емкости элемента. Отсюда следует, что отдельные группы полупроводниковых двухполюсников малой емкости будут при зарядке становиться больше, и наоборот, электроемкость большого размера будет нуждаться в меньшем заряде.

Существует также смешанное соединение двух и более конденсаторов. Здесь электрическая энергия распределяется одновременно при помощи параллельного и последовательного подключения электролитических элементов в цепь. Эта схема имеет несколько участков с различным подключением конденсирующих двухполюсников. Иными словами, на одном цепь параллельно включена, на другом – последовательно. Такая электрическая схема имеет ряд достоинств сравнительно с традиционными:
- Можно использовать для любых целей: подключения электродвигателя, станочного оборудования, радиотехнических приборов;
- Простой расчет. Для монтажа вся схема разбивается на отдельные участки цепи, которые рассчитываются по отдельности;
- Свойства компонентов не изменяются независимо от изменений электромагнитного поля, силы тока. Это очень важно при работе с разноименными двухполюсниками. Ёмкость постоянна при постоянном напряжении, но, при этом, потенциал пропорционален заряду;
- Если требуется собрать несколько неполярных полупроводниковых двухполюсников из полярных, то нужно взять несколько однополюсных двухполюсника и соединить их встречно-параллельным способом (в треугольник). Минус к минусу, а плюс к плюсу. Таким образом, за счет увеличения емкости изменяется принцип работы двухполюсного полупроводника.
Параллельное и последовательное соединение конденсаторов
Так же как резисторы, конденсаторы можно соединять последовательно и параллельно.
При параллельном соединении емкости складываются — ну это и понятно, это как заполнять сообщающиеся сосуды, общий объем получается равным сумме объемов. При последовательном же соединении получится так, что конденсатор с маленькой емкостью заполнится зарядом быстрее, чем конденсатор с большой емкостью. Напряжение на маленьком конденсаторе быстро вырастет почти до напряжения источника ( ну и остальные конденсаторы внесут свой вклад) , ток в общей цепи уменьшится до нуля, и процесс заряда конденсаторов прекратится. Таким образом емкость последовательно соединенных конденсаторов получается меньше емкости самого маленького из них.
Upd.
Рассмотрим более подробно процесс заряда конденсатора на схеме рис.10 (по мотивам учебника И.В.Савельева «Курс общей физики», том II. «Электричество» )
Как было сказано в предыдущей статье О природе электрического тока электрический ток — это движение заряженных частиц. В проводниках ( в отличие от диэлектриков-изоляторов) часть электронов является свободными и такие электроны могут перескакивать от одного атому к другому. В целом проводник электрически нейтрален — отрицательный заряд электронов компенсируется положительным зарядом ядер атомов. Чтобы заставить электроны двигаться нужно создать их избыток на одном конце проводника и недостаток на другом. Этот избыток электронов на одном полюсе создает батарейка вследствие протекающих в ней электрохимических реакций. Когда проводник присоединяется к полюсам батарейки электроны от полюса, где их избыток начинают двигаться к другому полюсу, потому что одноименные заряды отталкивают друг друга. Эти свободные электроны движутся внутри проводника по всему объему.
Движение электронов в RC цепи на рис. 3 имеет другой характер. Поскольку цепь не замкнута (обкладки конденсатора не соединены друг с другом) постоянный ток в цепи идти не может. Поэтому поступающий избыток электронов с полюса батарейки приводит к тому, что проводник теряет электрическую нейтральность. Избыточный заряд q, распределяется по поверхности проводника так, чтобы напряженность поля внутри проводника была равна нулю. Ну это понятно, одноименные заряды отталкиваются и стремятся расположиться подальше друг от друга, то есть на поверхности. Если бы не было резистора R, то перераспределение зарядов по поверхности происходило бы мгновенно. Однако резистор ограничивает ток ( движение зарядов) поэтому перераспределение происходит постепенно. По мере зарядки конденсатора напряжение на нем растет и ток через резистор уменьшается. Избыточные электроны концентрируются на одной обкладке и создают электрическое поле. Это поле отталкивает электроны, находящиеся на другой обкладке и «проталкивает» их дальше по проводнику к отрицательному полюсу батареи. (Знаки + и — в данном случае берем условно). Таким образом в незамкнутой цепи протекает ток заряда конденсатора. Этот ток не постоянный и уменьшается со временем. Однако, если в какой-то момент поменять полярность батареи, то ток потечет уже в обратную сторону. Если это переключение делать достаточно часто, так чтобы конденсатор не успевал полностью зарядиться, то в цепи все время будет течь ток, то в одну, то в другую сторону. Это и происходит, когда говорят, что «конденсатор проводит переменный ток».
Для плоского конденсатора емкость равна С=ε0*ε*S/d , где d – зазор между обкладками, ε – диэлектрическая проницаемость вещества, заполняющего зазор, S — площадь обкладок.
То есть на емкость влияет не только площадь обкладок и расстояние между ними, но и материал диэлектрика, который между обкладками помещен. Причем на емкость конденсатора материал диэлектрика может влиять достаточно сильно, с разными дополнительными эффектами, см. например статью «Поляризация диэлектрика»
Литература
«Драма идей в познании природы», Зельдович Я.Б., Хлопов М.Ю., 1988
«Курс общей физики», том II. «Электричество» И.В.Савельев
Википедия — статьи про электричество.
Параллельное соединение конденсаторов.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).

Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
![]()
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Последовательное соединение конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).

Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Что ещё необходимо знать, чтобы правильно соединять конденсаторы?
Во-первых, не стоит забывать, что есть ещё один немаловажный параметр, как номинальное напряжение.
При последовательном соединении конденсаторов напряжение между ними распределяется обратно пропорционально их ёмкостям. Поэтому, есть смысл при последовательном соединении применять конденсаторы с номинальным напряжением равным тому, которое имеет конденсатор, взамен которого мы ставим составной.
Если же используются конденсаторы с одинаковой ёмкостью, то напряжение между ними разделится поровну.
Для электролитических конденсаторов.
При соединении электролитических конденсаторов (электролитов) строго соблюдайте полярность! При параллельном соединении всегда подключайте минусовой вывод одного конденсатора к минусовому выводу другого,а плюсовой вывод с плюсовым.

Параллельное соединение электролитов

Схема параллельного соединения
В последовательном соединении электролитов ситуация обратная. Необходимо подключать плюсовой вывод к минусовому. Получается что-то вроде последовательного соединения батареек.

Последовательное соединение электролитов

Схема последовательного соединения
Также не забывайте про номинальное напряжение. При параллельном соединении каждый из задействованных конденсаторов должен иметь то номинальное напряжение, как если бы мы ставили в схему один конденсатор. То есть если в схему нужно установить конденсатор с номинальным напряжением на 35 вольт и ёмкостью, например, 200 микрофарад, то взамен его можно параллельно соединить два конденсатора на 100 микрофарад и 35 вольт. Если хоть один из них будет иметь меньшее номинальное напряжение (например, 25 вольт), то он вскоре выйдет из строя.
Желательно, чтобы для составного конденсатора подбирались конденсаторы одного типа (плёночные, керамические, слюдяные, металлобумажные). Лучше всего будет, если они взяты из одной партии, так как в таком случае разброс параметров у них будет небольшой.
Конечно, возможно и смешанное (комбинированное) соединение, но в практике оно не применяется (я не видел ). Расчёт ёмкости при смешанном соединении обычно достаётся тем, кто решает задачи по физике или сдаёт экзамены 🙂
Тем же, кто не на шутку увлёкся электроникой непременно надо знать, как правильно соединять резисторы и рассчитывать их общее сопротивление!
Маркировка конденсаторов.
Существует несколько основных способов маркировки, давайте рассмотрим их в порядке очередности. Итак, один из вариантов — это маркировка тремя цифрами, например так:
- если третья цифра от 0 до 5, то емкость в пикофарадах необходимо умножить на 10 в соответствующей степени. Степень как раз и определяется третьим числом
- если третья цифра — 8, то величину емкости умножаем на 0.01
- если третья цифра — 9, то величину емкости умножаем на 0.1
Давайте на практическом примере разберемся как же определить емкость, руководствуясь этими правилами — определим электроемкость изображенных на рисунке конденсаторов.
Для первого из них имеем маркировку «470» — первые две цифры — 47 — значит емкость равна 47 пФ. Множитель равен 0, тогда емкость определяется следующим образом:
C= 47 cdot 10^0 = 47medspace пФ
Запишем аналогичные выражения для последующих конденсаторов:
C_2= 15 cdot 0.1 = 1.5medspace пФ
C_3 = 22cdot 10^3 = 22000medspace пФ = 22medspace нФ
C_4 = 47cdot 10^4 = 470000medspace пФ = 470medspace нФ
C_5 = 68cdot 10^2 = 680medspace пФ = 6.8medspace нФ
Как видите, здесь нет ничего сложного, поэтому плавно переходим к следующему способу.
Данный вариант маркировки почти не отличается от того, что мы уже обсудили. Отличие заключается только в том, что тут для обозначения величины емкости в пикофарадах используются три первые цифры (а не две), а четвертая цифра также обозначает множитель. Небольшой наглядный пример для этого случая и будем двигаться дальше:

По аналогии определяем емкость:
C = 475cdot 10^2 = 47500medspace пФ = 47.5medspace нФ
Иногда можно встретить маркировку тремя цифрами и буквой. В данном случае буква будет обозначать допустимое отклонение емкости от указанного цифрами значения:
Что именно означают эти цифры определяют в соответствии с таблицей:
Кроме того, возможна цифровая маркировка непосредственно емкости в микрофарадах. Десятичная запятая в этом случае заменяется латинской буквой R:
Емкость здесь определяется очень просто (не забываем, что буква R просто заменяет запятую):
C_1 = 0.47medspace мкФ
C_2 = 4.7medspace мкФ
И, наконец, еще одним способом маркировки является цифро-буквенная маркировка. В данном случае величина емкости указывается цифрами, а единица измерения буквой:
Причем здесь, также как и в предыдущем примере, если буква расположена между цифрами, то она выполняет роль десятичной запятой:
C_1 = 1.5medspace пФ
C_2 = 15medspace нФ
C_3 = 33.5medspace мкФ
C_4 = 1medspace мФ
На этом мы заканчиваем обсуждение маркировки конденсаторов и переходим к вариантам их соединения.
Последовательное соединение конденсаторов.
Как и в случае с резисторами первым делом рассмотрим последовательное соединение конденсаторов.
При таком соединении заряды всех конденсаторов окажутся равны:
q_1 = q_2 = q_3 = q
Вспомним формулу для напряжения из предыдущей статьи и определим величины:
U_1 = frac
U_2 = frac
U_3 = frac
А общее напряжение при последовательном соединении равно сумме напряжений на элементах схемы по отдельности:
U_0 = U_1 + U_2 + U_3
Но в то же время общее напряжение можно выразить через общую емкость цепи:
U_0 = frac
Приравниваем эти выражения и в результате получаем формулу для определения емкости при последовательном соединении конденсаторов:
frac = frac + frac + frac
Согласитесь, эта формула напоминает выражение для определения общего сопротивления при параллельном соединении резисторов (ссылка). С этим разобрались, продолжаем.
Последовательное и параллельное соединение
Соединение двух двухвыводных деталей в электрической схеме можно выполнить двумя способами.
Во-первых, можно соединить детали одним выводом, а оставшиеся свободные выводы подключить к схеме. Такое соединение называется последовательным.
Во-вторых, можно соединить оба вывода обоих деталей, а к линии подключить точки соединения. Такое соединение называется параллельным.
В последовательном и параллельном соединении может участвовать более двух деталей. В первом случае детали соединяются «цепочкой». Во втором случае все детали соединяются одноименными выводами, и две точки соединения подключаются к схеме.
Большинство электрических схем разлагаются на ряд последовательных и параллельных звеньев. Даже если это не так (когда есть узлы или компоненты с нечетным количеством выводов), в схеме всё равно, как правило, имеется множество последовательно и параллельно соединенных участков.
Емкость соединенных конденсаторов
Заметим, что как бы ни были соединены конденсаторы, если в рассматриваемом соединении нет других элементов, то такой участок схемы может только накапливать и отдавать заряд. Никаких других электрических преобразований здесь нет. А значит, с точки зрения внешней схемы, несколько конденсаторов представляют также конденсатор некоторой емкости. Однако эта емкость будет, конечно, отличаться от емкости составляющих конденсаторов. Формулы последовательного и параллельного соединений конденсаторов также будут различны.
Емкость параллельного соединения конденсаторов находится по формуле:
Емкость последовательного соединения конденсаторов находится по формуле:
Запомнить сами формулы несложно: в обоих случаях результат равен сумме составляющих. Разница в том, что для первого случая составляющие и результат формулы — это сами емкости. А для второго случая — это обратные величины.
Запомнить, где какая формула используется, можно, учитывая два момента:
- емкость характеризует легкость зарядки конденсатора;
- при обычной сумме результат становится больше, при суммировании же обратных величин результат будет меньше.
Теперь остается представить, как распределяется общий заряд по параллельному и по последовательному соединению.
Если конденсаторы соединены параллельно, то это эквивалентно увеличению площади их обкладок. Большие по размеру обкладки «вмещают» больше электронов, зарядить их легче, емкость будет больше. Справедлива формула с суммой емкостей.
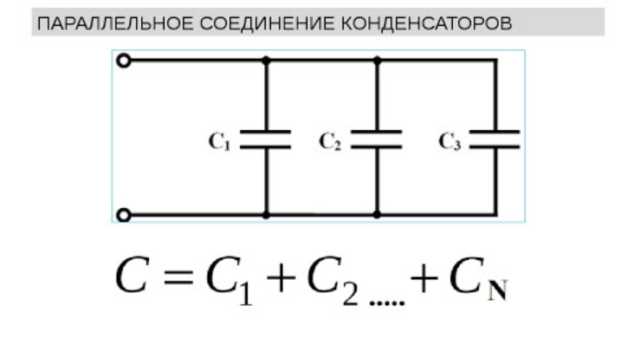
Если конденсаторы соединены последовательно, то для заряда каждого конденсатора необходимо преодолеть напряжение, которое имеется на всех остальных конденсаторах (они ведь тоже заряжаются), и по мере заряда это напряжение растет. Следовательно, последовательные конденсаторы зарядить труднее, емкость будет меньше. Справедлива формула с обратными значениями емкостей.
Формулы последовательного и параллельного соединения конденсаторов аналогичны формулам общего сопротивления для соединений резисторов, но используются «наоборот»: у резисторов формула с суммой значений используется в последовательном соединении, а формула с суммой обратных величин — в параллельном.




