На прошлых уроках мы уже упоминали о том, что электрическое поле обладает некоторой энергией. Значит, оно способно совершить какую-то работу. Эту работу называют работой электрического тока.
А теперь вспомним уже известное нам определение механической работы. Она определяется силой, действующей на тело, и расстоянием, на которое это тело перемещается: $A = Fs$.
Если мы перенесем эти знания на электрические явления, то сможем сказать, что работа тока — это работа электрических сил, которые перемещают заряженные частицы в проводнике. Но если мы будем использовать формулу $A = Fs$ для каждой частицы, то последующие расчеты будут невероятно сложными. Ведь тогда нам нужно будет знать и точное количество заряженных частиц, и точное расстояние, которое они прошли под действием сил электрического поля.
Мы пойдем другим путем. Он будет гораздо проще и понятнее. На данном уроке мы дадим определение работы электрического тока через другие электрические величины (силу тока, напряжение, электрический заряд). Также мы научимся рассчитывать работу электрического тока, используя полученные знания.
Работа электрического тока и напряжение
Чему равно электрическое напряжение на участке цепи?
Вспомним определение этой величины. Мы говорили, что напряжение на концах проводника (участка цепи) равно работе, которая совершается при прохождении по этому проводнику заряда, равному $1 space Кл$: $U = frac$.
Как через напряжение и электрический заряд, прошедший через участок цепи, выразить работу электрического тока на этом участке?
Используя формулу электрического напряжения, выразим работу электрического тока.
$A = Uq$.
Чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (количество электричества), прошедший по нему.
Закон Джоуля-Ленца
В случае, когда на участке цепи не совершается механическая работа, и ток не производит химических действий, происходит только нагревание проводника. Нагретый проводник отдает теплоту окружающим телам.
Закон, определяющий количество теплоты, которое выделяет проводник с током в окружающую среду, был впервые установлен экспериментально английским ученым Д. Джоулем (1818—1889) и русским Э.Х. Ленцем (1804—1865). Закон Джоуля—Ленца сформулирован следующим образом:
Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока по проводнику.
Количество теплоты измеряется в Джоулях (Дж).
Пример №2. Определить, какое количество теплоты было выделено за 2 минуты проводником при напряжении 12 В и сопротивлении 2 Ом.
Урок 163 (осн). Работа и мощность электрического тока
Используем закон Ома и закон Джоуля—Ленца:
Q = I 2 R Δ t = ( U R . . ) 2 Δ t = U 2 R . . Δ t = 12 2 2 . . = 72 ( Д ж )
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P = I U = I 2 R = U 2 R . .
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P = I 2 R = 0 , 3 2 · 10 = 0 , 9 ( В т )
Выразив силу тока через заряд, прошедший за единицу времени, получим:
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P = ( ε R + r . . ) 2 R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
P m a x = ( ε r + r . . ) 2 r = ε 2 4 r . .
Мощность тока внутренней цепи:
P в н у т р = I 2 r = ( ε R + r . . ) 2 r
P п о л н = I 2 ( R + r ) = ε 2 R + r . .
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P = ( ε R + r . . ) 2 R
Применим закон Ома для полной цепи:
Выразим сопротивление внешней цепи:
P = ( ε ε I . . − r + r . . ) 2 ( ε I . . − r ) = I 2 ( ε I . . − r ) = I ε − r I 2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
r I 2 − I ε + P = 0
I 2 − 1 I + 0 , 75 = 0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
Работа и мощность тока
При прохождении тока в цепи электрическое поле совершает работу по перемещению заряда. В этом случае работу электрического поля называют работой электрического тока.
При прохождении заряда (q) по участку цепи электрическое поле будет совершать работу: (A=qcdot U), где (U) — напряжение электрического поля, (A) — работа, совершаемая силами электрического поля по перемещению заряда (q) из одной точки в другую.
Для выражения любой из этих величин можно использовать приведённый ниже рисунок.
Рис. (1). Зависимость между работой, напряжением и зарядом
Количество заряда, прошедшее по участку цепи, пропорционально силе тока и времени прохождения заряда: q = I ⋅ t .
Работа электрического тока на участке цепи пропорциональна напряжению на её концах и количеству заряда, проходящего по этому участку: A = U ⋅ q .
Работа электрического тока на участке цепи пропорциональна силе тока, времени прохождения заряда и напряжению на концах участка цепи: A = U ⋅ I ⋅ t .
Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком.

Рис. (2). Зависимость между работой, силой тока и временем прохождения заряда
Единицы измерения величин:
работа электрического тока ([A]=1) Дж;
напряжение на участке цепи ([U]=1) В;
сила тока, проходящего по участку ([I]=1) А;
время прохождения заряда (тока) ([t]=1) с.
Для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображённую на рисунке. Вольтметром измеряется напряжение на лампе, амперметром — сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.
Рис. (3). Схема и часы для измерения
I = 1 , 2 А U = 5 В t = 1 , 5 мин = 90 с А = U ⋅ I ⋅ t = 5 ⋅ 1 , 2 ⋅ 90 = 540 Дж
Обрати внимание!
Работа чаще всего выражается в килоджоулях или мегаджоулях.
(1) кДж = 1000 Дж или (1) Дж = (0,001) кДж;
(1) МДж = 1000000 Дж или (1) Дж = (0,000001) МДж.
Для потребителей электрической энергии существуют приборы, позволяющие в пределах ошибки измерения получать числовые данные о ее расходе в единицу времени.

Рис. (4). Электросчетчик
Механическая мощность численно равна работе, совершённой телом в единицу времени: N = А t . Чтобы найти мощность электрического тока, надо поступить точно также, т.е. работу тока, A = U ⋅ I ⋅ t , разделить на время.
Мощность электрического тока обозначают буквой (Р):
P = A t = U ⋅ I ⋅ t t = U ⋅ I . Таким образом:
Мощность электрического тока равна произведению напряжения на силу тока: P = U ⋅ I .
Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведённый ниже рисунок.
Рис. (5). Зависимость между мощностью, напряжением и силой тока
За единицу мощности принят ватт: (1) Вт = (1) Дж/с.
Из формулы P = U ⋅ I следует, что
(1) ватт = (1) вольт ∙ (1) ампер, или (1) Вт = (1) В ∙ А.
Обрати внимание!
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
(1) гВт = (100) Вт или (1) Вт = (0,01) гВт;
(1) кВт = (1000) Вт или (1) Вт = (0,001) кВт;
(1) МВт = (1 000 000) Вт или (1) Вт = (0,000001) МВт.
Измерим силу тока в цепи с помощью амперметра, а напряжение на участке — с помощью вольтметра.
Рис. (6). Схема
Так как мощность тока прямо пропорциональна напряжению и силе тока, протекающего через лампочку, то перемножим их значения:
I = 1 , 2 А U = 5 В P = U ⋅ I = 5 ⋅ 1 , 2 = 6 Вт .
Ваттметры измеряют мощность электрического тока, протекающего через прибор. По своему назначению и техническим характеристикам ваттметры разнообразны.
В зависимости от сферы применения у них различаются пределы измерения.
Аналоговый ваттметр
Аналоговый ваттметр
Аналоговый ваттметр
Цифровой ваттметр




Рис. (7). Приборы для измерения
Подключим к цепи по очереди две лампочки накаливания, сначала одну, затем другую и измерим силу тока в каждой из них. Она будет разной.


Рис. (8). Лампы различной мощности в цепи
Сила тока в лампочке мощностью (25) ватт будет составлять (0,1) А. Лампочка мощностью (100) ватт потребляет ток в четыре раза больше — (0,4) А. Напряжение в этом эксперименте неизменно и равно (220) В. Легко можно заметить, что лампочка в (100) ватт светится гораздо ярче, чем (25)-ваттовая лампочка. Это происходит оттого, что её мощность больше. Лампочка, мощность которой в (4) раза больше, потребляет в (4) раза больше тока. Значит:
Обрати внимание!
Мощность прямо пропорциональна силе тока.
Что произойдёт, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение (110) В и (220) В.
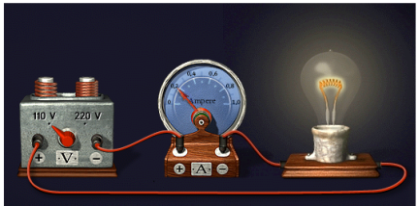

Рис. (8). Лампа, подключенная к источнику тока с различным напряжением
Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае её мощность будет больше. Следовательно:
Обрати внимание!
Мощность зависит от напряжения.
Рассчитаем мощность лампочки в каждом случае:
| I = 0 , 2 А U = 110 В P = U ⋅ I = 110 ⋅ 0 , 2 = 22 Вт | I = 0,4 А U = 220 В P = U ⋅ I = 220 ⋅ 0,4 = 88 Вт . |
Можно сделать вывод о том, что при увеличении напряжения в (2) раза мощность увеличивается в (4) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно, ток через нить накала и её расчётное сопротивление) указывается только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).
 |  |  |
Работа электрического тока. Закон Джоуля-Ленца.
Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: .

Для определения работы, которая совершается током, проходящим по некоторому участку цепи, нужно воспользоваться определением напряжения: . Значит,
где А — работа тока; q — электрический заряд, который прошел за определенное время через исследуемый участок цепи. Подставив в последнее равенство формулу q = It, имеем:
Работа электрического тока на участке цепи является произведением напряжения на концах этого участка на силу тока и на время, на протяжении которого совершалась работа.
Закон Джоуля-Ленца .
Закон Джоуля — Ленца гласит: количество теплоты, которое выделяется в проводнике на участке электрической цепи с сопротивлением R при протекании по нему постоянного тока I в течение времени t равно произведению квадрата тока на сопротивление и время:
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца видно, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это применяется в технике, например, для распыления металлов.

При параллельном соединении каждый проводник находятся под одинаковым напряжением, но токи в них разные. Из формулы (Q = I 2 Rt) видно, что, так как, согласно закону Ома , то

Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле (А = IUt) выразить U через IR, воспользовавшись законом Ома, получим Закон Джоуля — Ленца. Это лишний раз подтверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
§ 50. Работа электрического тока
Как вычислить работу электрического тока? Мы уже знаем, что напряжение на концах участка цепи численно равно работе, которая совершается при прохождении по этому участку электрического заряда в 1 Кл. При прохождении по этому же участку электрического заряда, равного не 1 Кл, а, например, 5 Кл, совершённая работа будет в 5 раз больше. Таким образом, чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (количество электричества), прошедший по нему:
где А — работа, U — напряжение, q — электрический заряд. Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения:
Используя это соотношение, получим формулу работы электрического тока, которой удобно пользоваться при расчётах:
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.
Работу измеряют в джоулях, напряжение — в вольтах, силу тока — в амперах и время — в секундах, поэтому можно написать:
1 джоуль = 1 вольт х 1 ампер х 1 секунду,
1 Дж = 1 В • А • с.
Выходит, что для измерения работы электрического тока нужны три прибора: вольтметр, амперметр и часы. На практике работу электрического тока измеряют специальными приборами — счётчиками. В устройстве счётчика как бы сочетаются три названных выше прибора. Счётчики электроэнергии сейчас можно видеть почти в каждой квартире.
Пример. Какую работу совершает электродвигатель за 1 ч, если сила тока в цепи электродвигателя 5 А, напряжение на его клеммах 220 В? КПД двигателя 80% .
Запишем условие задачи и решим её.

Вопросы
- Чему равно электрическое напряжение на участке цепи?
- Как через напряжение и электрический заряд, прошедший через участок цепи, выразить работу электрического тока на этом участке?
- Как выразить работу тока через напряжение, силу тока и время?
- Какими приборами измеряют работу электрического тока?
- Какую работу совершает электрический ток в электродвигателе за 30 мин, если сила тока в цепи 0,5 А, а напряжение на клеммах двигателя 12 В?
- Напряжение на спирали лампочки от карманного фонаря равно 3,5 В, сопротивление спирали 14 Ом. Какую работу совершает ток в лампочке за 5 мин?
- Два проводника, сопротивлением по 5 Ом каждый, соединены сначала последовательно, а потом параллельно и в обоих случаях включены под напряжение 4,5 В. В каком случае работа тока за одно и то же время будет больше и во сколько раз?
Работа и мощность электрического тока. Закон Джоуля-Ленца
1. Электрический ток, проходя по цепи, производит разные действия: тепловое, механическое, химическое, магнитное. При этом электрическое поле совершает работу, и электрическая энергия превращается в другие виды энергии: во внутреннюю, механическую, энергию магнитного поля и пр.
Как было показано, напряжение ( (U) ) на участке цепи равно отношению работы ( (F) ) , совершаемой при перемещении электрического заряда ( (q) ) на этом участке, к заряду: ( U=A/q ) . Отсюда ( A=qU ) . Поскольку заряд равен произведению силы тока ( (I) ) и времени ( (t) ) ( q=It ) , то ( A=IUt ) , т.е. работа электрического тока на участке цепи равна произведению напряжения на этом участке, силы тока и времени, в течение которого совершается работа.
Единицей работы является джоуль (1 Дж). Эту единицу можно выразить через электрические единицы:
( [A] ) = 1 Дж = 1 В · 1 А · 1 с
Для измерения работы используют три измерительных прибора: амперметр, вольтметр и часы, однако, в реальной жизни для измерения работы электрического тока используют счётчики электрической энергии.
Если нужно найти работу тока, но при этом сила тока или напряжение неизвестны, то можно воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: ( A=fract ) или ( A=I^2Rt ) .
2. Мощность электрического тока равна отношению работы ко времени, за которое она совершена: ( P=A/t ) или ( P=IUt/t ) ; ( P=IU ) , т.е. мощность электрического тока равна произведению напряжения и силы тока в цепи.
Единицей мощности является ватт (1 Вт): ( [P]=[I]cdot[U] ) ; ( [P] ) = 1 А · 1 В = 1 Вт.
Используя закон Ома, можно получить другие формулы для расчета мощности тока: ( P=frac;P=I^2R ) .
Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра, измерив соответственно силу тока и напряжение. Можно для измерения мощности использовать специальный прибор, называемый ваттметром, в котором объединены амперметр и вольтметр.
3. При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: ( Q=A ) или ( Q=IUt ) . Учитывая, что ( U=IR ) , ( Q=I^2Rt ) .
Количество теплоты, выделяющееся при прохождении тока но проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени.
Этот закон называют законом Джоуля-Ленца.
ПРИМЕРЫ ЗАДАНИЙ
1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
3. Сопротивления резистор ( R_1 ) в четыре раза меньше сопротивления резистора ( R_2 ) . Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1
4. Сопротивление резистора ( R_1 ) в 3 раза больше сопротивления резистора ( R_2 ) . Количество теплоты, которое выделится в резисторе 1
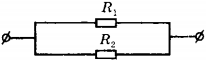
1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2
5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если
1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока ( A_1 ) и ( A_2 ) в этих проводниках за одно и то же время.
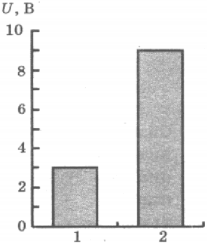
1) ( A_1=A_2 )
2) ( A_1=3A_2 )
3) ( 9A_1=A_2 )
4) ( 3A_1=A_2 )
7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока ( A_1 ) и ( A_2 ) в этих проводниках за одно и то же время.
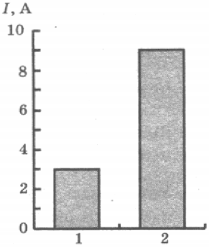
1) ( A_1=A_2 )
2) ( A_1=3A_2 )
3) ( 9A_1=A_2 )
4) ( 3A_1=A_2 )
8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то
А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.
Верным(-и) является(-ются) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?
1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А
10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?
1) 10000 с
2) 2000 с
3) 10 с
4) 2 с
11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась
12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока
Интерпретация закона сохранения энергии. Закон Джоуля-Ленца
Закон Ома для однородного участка цепи при сопротивлении R отражает формула:
Умножим обе части выражения на I Δ t и получим соотношение:
R I 2 ∆ t = U I ∆ t = ∆ A .
Полученный результат является выражением закона сохранения энергии для однородного участка цепи.
Работа Δ A электрического тока I , протекающего по неподвижному проводнику с сопротивлением R , преобразуется в тепло Δ Q , выделяющееся на проводнике.
∆ Q = ∆ A = R I 2 ∆ t
Данный закон называется законом Джоуля-Ленца.
Закон носит название сразу двух известных физиков, поскольку экспериментальным путем был установлен ими обоими в независимости друг от друга.
Мощность электрического тока есть отношение работы тока Δ A к интервалу времени Δ t , за которое эта работа была произведена.
Можно сказать проще: мощность – это работа, выполненная в единицу времени. Запишем формулу, связывающую работу тока и его мощность:
P = ∆ A ∆ t = U I = I 2 R = U 2 R
Работу электрического тока выражают в джоулях ( Д ж ) , мощность тока измеряется в ваттах ( В т ) , время – в секундах ( с ) : 1 В т = 1 Д ж 1 с . Измерение мощности тока происходит при помощи ваттметра, а работа находится расчетно как результат перемножения силы тока, напряжения и времени протекания тока по цепи: A = I U t .
Следующей разберем полную цепь постоянного тока, включающую в себя источник с электродвижущей силой δ и внутренним сопротивлением r и внешний однородный участок с сопротивлением R .
Закон Ома для полной цепи выглядит так:
Перемножим обе части выражения с Δ q = I Δ t и получим соотношение, которое будет служить выражением закона сохранения энергии для полной цепи постоянного тока:
R I 2 ∆ t + r I 2 ∆ t = δ I ∆ t = ∆ A с т
Левая часть выражения содержит Δ Q = R I 2 Δ t (тепло, которое выделяется на внешнем участке цепи за время Δ t ) и Δ Q и с т = r I 2 Δ t (тепло, которое выделяется внутри источника за такое же время).
Выражение δ I Δ t является равным работе сторонних сил Δ A с т , которые действуют внутри источника.
При протекании электрического тока по замкнутой цепи происходит преобразование работы сторонних сил Δ A с т в тепло, которое выделяется во внешней цепи ( Δ Q ) и внутри источника ( Δ Q и с т ) .
∆ Q + Q и с т = ∆ A с т = δ I ∆ t
Необходимо отметить следующий факт: в указанное соотношение не включена работа электрического поля. Когда ток проходит по замкнутой цепи, электрическое поле работы не совершает; значит тепло производится лишь посредством сторонних сил, которые действуют внутри источника. Электрическое поле здесь выполняет перераспределение тепла между различными участками цепи.
Внешней цепью может служить не только проводник с сопротивлением R , но и какое-то устройство, которое потребляет мощность, к примеру, электродвигатель постоянного тока. Тогда R необходимо расценивать как эквивалентное сопротивление нагрузки. Энергия, которая выделится во внешней цепи, имеет возможность частично или полностью преобразоваться как в тепло, так и в иные виды энергии, к примеру, в механическую работу, совершаемую электродвигателем. Таким образом, тема использования энергии источника тока имеет важное практическое значение.
Коэффициент полезного действия источника
Полная мощность источника (или работа, которая производится посредством сторонних сил за единицу времени) составляет:
P и с т = δ I = δ 2 R + r
Внешняя цепь выделяет мощность:
P = R I 2 = δ I — r I 2 = δ 2 R ( R + r ) 2
Отношение η = P P и с т равное η = P P и с т = 1 — r δ I = R R + r , носит название коэффициента полезного действия источника.
На рис. 1 . 11 . 1 изображена зависимость мощности источника P и с т , полезной мощности P , которая выделяется во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной δ , и внутренним сопротивлением r . Ток в цепи имеет возможность меняться в пределах от I = 0 (при R = ∞ ) до I = I к з = δ r (при R = 0 ).
Рисунок 1 . 11 . 1 . Зависимость мощности источника P и с т , мощности во внешней цепи P и КПД источника η от силы тока.
Изображенные графики показывают, что максимальная мощность во внешней цепи P m a x , составляющая P m a x = δ 2 4 r , может быть достигнута при R = r . При этом ток в цепи есть I m a x = 1 2 I к з = δ 2 r ; коэффициент полезного действия источника составляет 50 % . Максимальное значение КПД будет достигнуто при I → 0 , т. е. при R → ∞ . При коротком замыкании полезная мощность P = 0 и вся мощность выделятся внутри источника, что с большой вероятностью может обернуться его перегревом и разрушением. КПД источника в этом случае обратится в нуль.
Работа и мощность тока
Итак, чтобы найти работу тока на участке цепи, надо напряжение на концах этого участка U умножить на силу тока I и на время t, в течение которого совершалась работа.
Действие тока характеризуют не только работой A, но и мощностью P. Мощность тока показывает, какую работу совершает ток за единицу времени. Если за время t была совершена работа A, то мощность тока P = A/t. Подставляя в это равенство выражение (18.2), получаем
Итак, чтобы найти мощность электрического тока P, надо силу тока I умножить на напряжение U.
В Международной системе единиц (СИ) работу выражают в джоулях (Дж), мощность — в ваттах (Вт), а время — в секундах (с). При этом
1 Вт = 1 Дж/с, 1 Дж = 1 Вт · с.
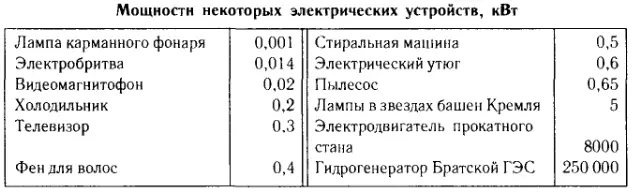
Мощности некоторых электроустройств, выраженные в киловаттах (1 кВт = 1000 Вт), приведены в таблице 5.
Рассчитаем наибольшую допустимую мощность потребителей электроэнергии, которые могут одновременно работать в квартире. Так как в жилых зданиях сила тока в проводке не должна превышать I = 10 А, то при напряжении U = 220 В соответствующая электрическая мощность оказывается равной:
P = 10 A · 220 В = 2200 Вт = 2,2 кВт.
Одновременное включение в сеть приборов с большей суммарной мощностью приведет к увеличению силы тока и потому недопустимо.
В быту работу тока (или израсходованную на совершение этой работы электроэнергию) измеряют с помощью специального прибора, называемого электрическим счетчиком (счетчиком электроэнергии). При прохождении тока через этот счетчик внутри его начинает вращаться легкий алюминиевый диск. Скорость его вращения оказывается пропорциональной силе тока и напряжению. Поэтому по числу оборотов, сделанных им за данное время, можно судить о работе, совершенной током за это время. Работа тока при этом выражается обычно в киловатт-часах (кВт·ч).
1 кВт·ч — это работа, совершаемая электрическим током мощностью 1 кВт в течение 1 ч. Так как 1 кВт = 1000 Вт, а 1 ч = 3600 с, то
1 кВт·ч = 1000 Вт · 3600 с = 3 600 000 Дж.
. 1. Как находится работа электрического тока? 2. По какой формуле находится мощность тока? 3. С помощью какого прибора измеряют работу тока? Какая единица работы при этом используется? 4. Сложите мощности всех имеющихся у вас дома электрических устройств. Допустимо ли их одновременное включение в сеть? Почему?
Экспериментальное задание. Рассмотрите у себя дома счетчик электроэнергии. Выясните, как снимаются с него показания. Измерьте с его помощью электроэнергию, израсходованную задень. В течение следующего дня старайтесь экономить энергию — не оставляйте включенным свет, если это не нужно; выключайте электроприборы, которыми в данный момент не пользуетесь; не смотрите все подряд по телевизору. После этого определите с помощью счетчика, сколько электроэнергии вам удалось сэкономить. Вычислите стоимость этой энергии. Сколько денег вам удастся сберечь при подобной экономии энергии за месяц?




