Все операции над числами в памяти компьютера выполняются не над самими числами, а над их машинными кодами .
Рассмотрим получение машинного кода целого положительного числа.
Предположим, что мы имеем дело с шестнадцатиразрядной сеткой. Вычислим диапазон целых чисел, которые можно представить. A min = 0 для целого положительного числа, а A max вычислим по формуле:
A max = 2 16 – 1 ; A max = 65535 .
Пример (1)
Запиши машинный код целого положительного числа (547) в шестнадцатиразрядной сетке.
1. Переведём число в двоичную систему счисления:
547 10 = 1000100011 2 .
2. Дополним недостающие разряды незначащими нулями для заполнения сетки:
A = 0000001000100011 2 .
3. Машинный код числа принято представлять в шестнадцатеричной системе счисления, так людям его удобнее воспринимать: K A = 0223 .
Ответ: K A = 0223 .
Такой код принято называть прямым кодом числа и обозначать [ K A ] ПК .
Рассмотрим получение машинного кода целого отрицательного числа.
Предположим, что мы имеем дело с шестнадцатиразрядной сеткой. Один из разрядов сетки, а именно самый старший разряд, будет отведён под хранение знака. Таким образом, для хранения самого числа у нас остаётся (15) разрядов. Вычислим диапазон целых чисел, которые можно представить. A min = − 2 15 = − 32768 для целого положительного числа, а A max вычислим по формуле:
A max = 2 15 – 1 ; A max = 32767 .
Обрати внимание: если мы сложим A min и A max , то получим (65535). То есть диапазон представляемых чисел не изменился.
Целые отрицательные числа хранятся в памяти в виде машинного кода дополнения к модулю исходного числа. Делается это для того, чтобы заменить операцию вычитания операцией сложения.
Для получения дополнительного кода используется следующий алгоритм:
1. получить двоичное представление модуля отрицательного числа.
2. Инвертировать все разряды полученного двоичного числа.
3. Прибавить к инвертированному числу (1).
прямой,обр,доп коды
Любая информация (числа, текстовая, графическая и т. д.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют битами. Двоичный код состоящий из 8 разрядов носит название байта.
Целые числа могут представляться в компьютере со знаком или без знака.
Представление целых чисел без знака в компьютере
Целые числа без знака обычно занимают в памяти компьютера один, два или 4 байта.
В однобайтовом формате числа принимают значения от 000000002 до 111111112.
В двубайтовом формате — от 00000000 000000002 до 11111111 111111112.
В четырехбайтовом — от 00000000 00000000 00000000 000000002 до 11111111 1111111 11111111 111111112
Прямой Обратный Дополнительный
Диапазоны значений целых чисел без знака
Формат числа в байтах
Запись с порядком
Например, в однобайтовом формате число 62=1111102 имеет вид:
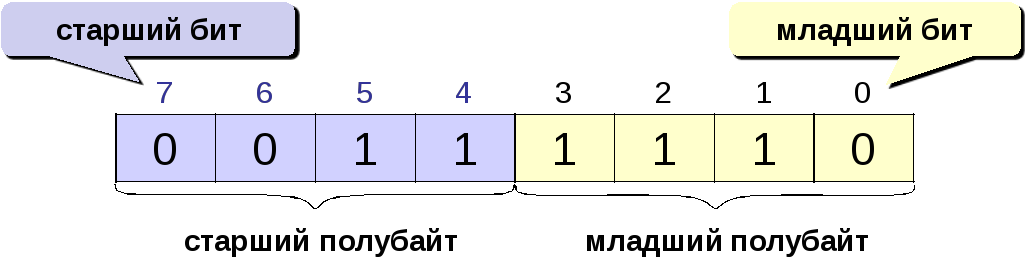
В двубайтовом формате число 1402=101011110102 имеет вид:

Пример 1. Для хранения целого числа без знака используется один
байт. Записать представление числа 19 в компьютере.
1 шаг: Переведем число 19 из десятичной системы счисления в двоичную.
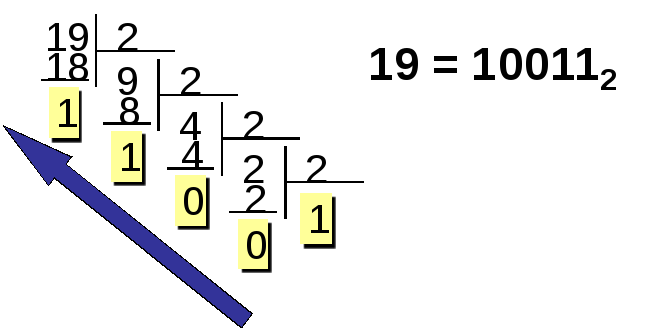
2 шаг: Так как для представления числа в компьютере выделен 1 байт, то код числа должен содержать 8 знаков (8 бит). Поэтому впереди числа дописываем 3 незначащих нуля.
1. Запишите числа в беззнаковом коде (формат 1 байт):
а) 31; б) 163; в) 65; г) 128.
2. Найдите десятичные представления чисел, записанных в беззнаковом коде:
а) 0 1011000; б) 1 0011011; в) 0 1101001; г) 1 1000000.
Представление целых чисел со знаком
Так же как беззнаковые целые числа целые со знаком обычно занимают в памяти компьютера один, два или 4 байта.
Диапазоны значений целых чисел со знаком
Формат числа в байтах
Запись с порядком
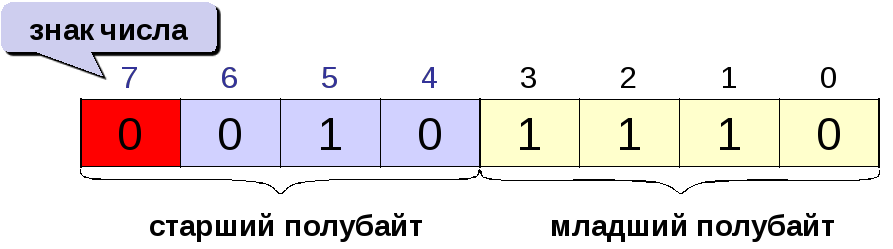
Самый левый (старший бит) разряд определяет знак числа. Если он равен 0, число положительное, если 1, то отрицательное.
Например, в однобайтовом формате число 46=1011102 имеет вид:
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Дополнительный код используется для хранения чисел в запоминающем устройстве ЭВМ. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Например, в однобайтовом формате числа 27 и -27 имеют вид:
Пример 1. Найти прямой, обратный и дополнительный код представления числа 13 в однобайтном формате.
1 шаг: Переведем число 13 из десятичной системы счисления в двоичную.
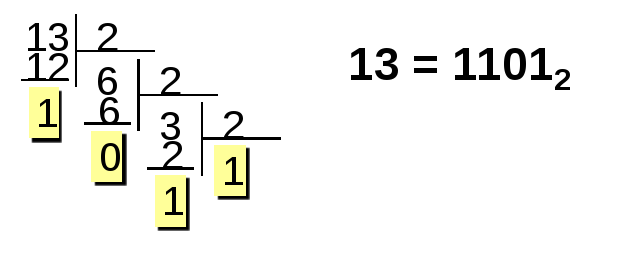
2 шаг: Для представления числа в компьютере выделен 1 байт. Старший бит занимает знак числа – 0. Сам код числа должен занимать 7 бит. Таким образом прямой код числа 13
Так как для положительных чисел прямой, обратный и дополнительный код совпадает, то ответ 00001101.
Пример 2. Найти прямой, обратный и дополнительный код представления числа -23 в однобайтовом формате.
1 шаг: Переведем число -23 из десятичной системы счисления в двоичную. Получим
2 шаг: Прямой код числа в однобайтовом формате, учитывая, что старший бит занимает знак числа -1, имеет вид
3 шаг: Найдем обратный код числа -23, заменив все цифры числа на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица. Имеем,
4 шаг: Найдем дополнительный код числа -23, добавив 1 к младшему разряду обратного кода.
Ответ: прямой код – 10010111; обратный – 11101000; дополнительный – 11101001.
Так вот, прямой обратный и дополнительный код — это модели представления целых чисел, как положительных, так и отрицательных. Примеры записи некоторых чисел во всех трех восьмиразрядных кодах показаны в таблице ниже.
Во всех трех кодах старший разряд указывает на знак числа и он равен единице, если число отрицательное и нулю в противном случае. Остальные разряды содержат представление модуля числа. Различие между кодами наблюдается именно в способах представления модуля. Для положительного числа модуль во всех трех кодах представляется одинаково — это просто естественная запись двоичного числа. Для отрицательных чисел, в обратном коде это просто поразрядная инверсия прямого кода, а в дополнительном — к обратному коду, как к числу, просто прибавляется единица.
Распространёнными формами представления чисел со знаками является их представление в прямом, обратном и дополнительном коде. Прямой код числа образуется кодированием знака числа нулём, если число положительно и единицей, если число отрицательно (для двоичной системы) Для общего случая (q — 1) — если число отрицательно, и 0 — если число положительно. q — основание системы счисления. Код знака записывается перед старшей цифрой числа и отделяется от неё точкой: -1.01 = 1.101 Прямой, обратный и дополнительный коды положительных чисел совпадают между собой. Обратный код отрицательного числа образуется из прямого кода, заменой его цифр на их дополнения до величины q-1. Код знака сохраняется без изменения. Пример : +12310 = 0.123пр = 0.123об. -12310 = 9.123пр = 9.876об +3А7С0016 = 0.3А7С00пр = 0.3А7С00об. -3А7С0016 = F.3А7С00пр= F.C583FFоб. -1012 = 1.101пр = 1.010об. Замена цифр их дополнениями для двоичной системы совпадает с операцией инверсии, то есть нули заменяются единицами, единицы — нулями. Знак принимает значение, равное единице. Дополнительный код отрицательного числа образуется из обратного увеличением на 1 его младшего разряда. При этом перенос из знакового разряда игнорируется. Пример: +23610 = 0.236пр.= 0.236об.= 0.236доп. -23610 = 9.236пр.= 9.763об.= 9.764доп. -1012= 1.101пр.= 1.010об= 1.011доп. -3А7С16= F.3А7Спр= F.C583об.= F.C584доп. Правила перевода из прямого кода в обратный и из обратного в прямой, а также из прямого в дополнительный и из дополнительного в прямой совпадают между собой.
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0 001 1001
-25= 1 110 0110
и складываем два числа:
0 110 0100 (100) + 1 110 0110 (-25) = 1 0 100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0 100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0 100 1010 + 1 = 0 100 1011 (знаковый бит = 0 , значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0 000 1010
-10= 1 111 0101
и складываем два числа:
0 000 0101 (5) + 1 111 0101 (-10) = 1 111 1010 (знаковый бит = 1 , значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1 111 1010 —-> 1 000 0101
Проверяем:
1 000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0 000 1010 —-> -10 = 1 000 1010
Инвертируем значение (получаем обратный код):
1 000 1010 —-> 1 111 0101
К полученной инверсии прибавляем 1:
1 111 0101 + 1 = 1 111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0 000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1 111 0110 — десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода
(42 голосов, оценка: 4,67 из 5)
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Число двоичных разрядов
Рассчитать
Представление положительного числа
Обратный код
Дополнительный код
Ссылка Сохранить Виджет
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А это все для удобной работы со знаками. Поскольку я все люблю понимать на примерах, рассказывать я тоже буду на примерах. Итак, предположим, что у нас 4 разряда для работы с двоичными числами. Представить таким образом можно 16 чисел — 0, 1, . 15
00 — 0000
.
15 — 1111
Но если нет знака, убогая получается арифметика. Нужно вводить знак. Чтобы никого не обидеть, половину диапазона отдадим положительным числам (8 чисел), половину — отрицательным (тоже 8 чисел). Ноль, что отличает машинную арифметику от обычной, мы отнесем в положительные числа (в обычной арифметике у нуля нет знака, если не ошибаюсь). Итого, в положительные числа попадают 0. 7, а в отрицательные -1, . -8.
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
Вот для их представления как раз и используется дополнительный код.
То есть, -7 в дополнительном коде получается так
прямой код 7 = 0111
обратный код 7 = 1000
дополнительный код 7 = 1001
Обратим внимание на то, что прямой код 1001 представляет число 9, которое отстоит от числа -7 ровно на 16, или .
Или, что тоже самое, дополнительный код числа «дополняет» прямой код до , т.е. 7+9=16
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
P.S. Ну а обратный код дополняет число до , или до всех 1, потому и называется дополнением до 1. Им тоже можно представлять отрицательные числа, и реализовать вычитание и сложение схемой сложения, только сложение там хитрее — с циклическим переносом, ну и представить можно меньше на одно число, так как все единицы уже заняты — это обратный код нуля, эдакий «минус нуль», то есть диапазон получается, если брать наш пример от -7 до 7. Не так удобно, одним словом.
Как это использовать?
Основную часть работы за вас проделывает сам используемый язык. В некоторых языках, например, C/C++, Rust или Swift, есть знаковые и беззнаковые типы. При этом в других вроде Java, Ruby и Python такого различия нет.
При использовании низкоуровневых языков, имеющих беззнаковые и знаковые типы данных, вы можете не понимать, что реализуете дополнительный код. Этот принцип неизменен, даже если вы не знаете, что конкретно происходит внутри процессора.
▍ Cи
#include #include int main() < // 8-битное беззнаковое целое число uint8_t unsignedEightBit = 255; // Максимальное значение для 8-битного беззнакового целого printf(«Unsigned 8-bit value: %un», unsignedEightBit); // 8-битное знаковое целое число int8_t signedEightBit = 127; // Максимальное значение для 8-битного знакового целого printf(«Signed 8-bit value: %dn», signedEightBit); // Демонстрация переполнения unsignedEightBit = 256; // Это значение вызовет переполнение printf(«Overflowed Unsigned 8-bit value: %un», unsignedEightBit); signedEightBit = 128; // Это значение вызовет переполнение printf(«Overflowed Signed 8-bit value: %dn», signedEightBit); return 0; >
- Для 8-битных беззнаковых целых чисел используется тип uint8_t . Он может хранить значения от 0 до 255.
- Для знаковых 8-битных целых чисел используется тип int8_t . Он может хранить значения от -128 до 127.
▍ Rust
В Rust для 8-битных беззнаковых целых используется тип u8 , а для 8-битных знаковых – тип i8 . Этот язык предоставляет богатую систему типов и возможности безопасности, включая проверку на целочисленные переполнения в отладочных сборках. Вот пример, демонстрирующий использование обоих типов:
fn main() < // 8-битное беззнаковое целое число let unsigned_eight_bit: u8 = 255; // Максимальное значение для 8-битного беззнакового целого println!(«Unsigned 8-bit value: <>», unsigned_eight_bit); // 8-битное знаковое целое число let signed_eight_bit: i8 = 127; // Максимальное значение для 8-битного знакового целого println!(«Signed 8-bit value: <>», signed_eight_bit); // Демонстрация переполнения // Примечание: в случае переполнения в режиме отладки в Rust активируется механизм паники // Для обработки переполнения можно использовать wrapping_add, saturating_add и тому подобное let overflowed_unsigned = unsigned_eight_bit.wrapping_add(1); println!(«Overflowed Unsigned 8-bit value: <>», overflowed_unsigned); let overflowed_signed = signed_eight_bit.wrapping_add(1); println!(«Overflowed Signed 8-bit value: <>», overflowed_signed); >
- Для 8-битных беззнаковых целых чисел используется тип u8 , способный хранить значения от 0 до 255.
- Для 8-битных знаковых целых используется тип i8 , способный хранить значения от -128 до 127.
Как это реализовать на ассемблере?
Я всё ещё предпочитаю обучать людей ассемблеру начиная с ассемблера 6502. Он прост и прекрасно помогает понять основы работы компьютеров. Это также позволяет познакомиться с дополнительным кодом, поскольку внутри процессора мы ограничены работой с 8-битными значениями.
▍ Ассемблер 6502
В ассемблере 6502 понятие знаковых и беззнаковых целых чисел не определяется явно через типы данных, как это происходит в высокоуровневых языках. Вместо этого способ их различения определяется тем, как вы управляете данными в коде. Отмечу, что процессор 6502 работает с 8-битными данными и 16-битными адресами.
Ниже показан пример обработки знаковых и беззнаковых 8-битных значений на ассемблере 6502:
LDA #$FF ; Загрузка в аккумулятор 8-битного значения (255 в десятичном виде или -1, если интерпретировать его как знаковое) STA $0200 ; Сохранение значения в области памяти $0200 LDA #$7F ; Загрузка в аккумулятор 127 (максимальное положительное значение для 8-битного знакового целого) STA $0201 ; Сохранение значения в области памяти $0201
- Инструкция LDA #$FF загружает в регистр-аккумулятор значение 0xFF (255 в десятичной системе). Если интерпретировать его, как беззнаковый байт, то получится 255. Если же трактовать его как знаковый байт (используя дополнительный код), то значением будет -1.
- Инструкция LDA #$7F загружает в аккумулятор значение 0x7F (127 в десятичной системе), являющегося максимумом для знакового 8-битного целого в представлении дополнительного кода.
Например, инструкции BPL (ветвление, если плюс) и BMI (ветвление, если минус) можно использовать для реализации ветвления на основе того, к какому знаковому числу привела последняя операция (положительному или отрицательному). При этом для сравнения беззнаковых целых чисел используются инструкции вроде BCS (ветвление, если перенос установлен) и BCC (ветвление, если переноса нет).
Это подобно вождению авто с механической коробкой передач. Автомобилю не важно, вперёд вы едете или назад – выбор нужной передачи за вами. Здесь комфортная и экономичная езда будет зависеть от своевременного включения правильной передачи. И те, кто ездит на механике, знает, что оно того стоит. Иногда.
Если у вас нет доступа к компьютеру с процессором 6502, то вы можете использовать эмулятор или онлайн-ассемблер. Мне нравится этот.
Пример программного преобразования
Если происходит чтение данных из файла или области памяти, где они хранятся в двоичном дополнительном коде (например, файл WAVE), может оказаться необходимым преобразовать байты. Если данные хранятся в 8 битах, необходимо, чтобы значения 128-255 были отрицательными.
C# .NET / C style
byte b1 = 254; //11111110 (бинарное) byte b2 = 121; //01111001 (бинарное) int c = (int)Math.Pow(2,(sizeof(byte)*8)-1); //2 возводится в степень 7. Результат: 10000000 (бинарное) int b1Conversion=(c ^ b1) — c; //Результат: -2. А фактически, двоичный дополнительный код. int b2Conversion=(c ^ b2) — c; //Результат остаётся 121, потому что знаковый разряд — нуль.
One’s complement, and two’s complement binary codes
This online calculator displays one’s complement and two’s complement codes for the entered negative integer.
In fact, this calculator displays binary code for any integer number, but the code depends on a sign. For positive integers, the calculator displays their binary representation. For negative integers, the calculator displays their representation both as one’s complement (also known as inverse code) and two’s complement (or simply complement code).
You can find the text explaining the logic behind one’s complement and two’s complement codes below the calculator
One’s complement and two’s complement codes
Number of bits
Binary code
One’s complement (inverse code)
Two’s complement (complement code)
Link Save Widget
Binary code is the binary representation of unsigned integers. If we’re talking about computers, there is a certain number of bits (binary digits) used to represent the number. So, the total range which n bits can represent is
One’s complement or inverse code is the inverted binary code of a number. That is, all zeroes become ones and all ones become zeroes.
Two’s complement or complement code is inverse code plus one
Now, what is it all about?
These codes were invented to make sign operations more comfortable (for machines). Since I’m the kind of person who likes to learn by example, I’ll explain this by example.
Let’s assume we have a computer with 4-bits binary numbers. A total range, which four bits can represent, is 16, starting from 0,1. to 15. Here are the binary representations:
00 — 0000
.
15 — 1111
But these are unsigned numbers and are not of much use. We need to introduce a sign. So, let’s take half of the range for positive numbers (eight, including zero), and half of the range — for negative (also eight). Note that the machine considers zero as a positive number, unlike usual math.
So, our positives will be 0. 7, and negatives will be -1. -8.
To distinguish positive and negative numbers, we assign the left-most bit as sign bit. Zero in sign bit tells as that this is a positive number and one — negative.
Positive numbers are represented by plain binary code:
7 — 0111
6 — 0110
.
1 — 0001
0 — 0000
But how can negative numbers be represented? Here come the one’s complement and two’s complement codes.
Let’s look at -7. Its absolute value is 7, which gives us 0111 in binary form. The one’s complement is the inversion of bits of absolute value, where all 0 become 1 and all 1 become 0. So, -7’s one’s complement or inverse code is 1000. The two’s complement is the inversion code plus one. So, -7’s two’s complement is 1001.
Note, that by itself, binary 1000 is 8, which, being added to 7 given 15, or . 15 is represented by 1111 (all bits are ones) in binary form, that’s the name — one’s complement — it «complements» binary code to , (all ones).
And binary 1001 is 9, which differs from -7 by 16, or . Or, which is the same, two’s complement code «complements» binary code to , i.e. 7+9=16
The latter was proved to be very useful for machine computation — usage of two’s complement code to represent negatives allows engineers to use an addition scheme for both addition and subtraction, thus simplifying the design of ALU (arithmetic and logical unit — a part of the processor). The two’s complement code easily detects overflow, and the situation when there are not enough bits to represent the given number.
| the summand | 7 | 0111 | 0111 | N/A | N/A |
| the summand | -3 | 1101 | 0011 | 1100 | 1101 |
| the sum | 4 | 0100 | 0100 | N/A | N/A |
| the summand | -1 | 1111 | 0001 | 1110 | 1111 |
| the summand | 7 | 0111 | 0111 | N/A | N/A |
| the sum | 6 | 0110 | 0110 | N/A | N/A |
Overflow is detected by looking at the two last carries, including carrying beyond the right-most bit. If carry bits are 11 or 00, there is no overflow; if carry bits are 01 or 10, there is an overflow. And, if there is no overflow, carry beyond the right-most bit can be safely ignored.
Some examples with carries and a fifth bit (a bit beyond right-most bit)
| the summand | 7 | 0111 |
| the summand | 1 | 0001 |
| the carries | 01110 | |
| the result | overflow | 01000 |
The two last carries are 01. This gives a signal of overflow
| the summand | -7 | 1001 |
| the summand | 7 | 0111 |
| the carries | 11110 | |
| the result | 0 | 10000 |
The result of addition 16 — but the fifth bit can be ignored; the real result is 0. The two last carries are 11. There is no overflow, so the correct result is indeed zero.
Overflow check can be done by simply XOR-ing two last carry bits.
Because of these convenient properties, two’s complement is the most common method to represent negative numbers on computers.
P.S. The one’s complement code also can be used to represent negatives, but the addition scheme should employ cyclic carry and is more complex. The range, which n bits can represent, is reduced by one since 1111 is busy as inverted 0000 — negative zero. So, it is less convenient.
Прямой, обратный и дополнительный коды
Очень часто в вычислениях должны использоваться не только положительные, но и отрицательные числа.
Число со знаком в вычислительной технике представляется путем представления старшего разряда числа в качестве знакового .
Принято считать, что 0 в знаковом разряде означает знак «плюс» для данного числа, а 1 – знак «минус».

Выполнение арифметических операций над числами с разными знаками представляется для аппаратной части довольно сложной процедурой. В этом случае нужно определить большее по модулю число, произвести вычитание и присвоить разности знак большего по модулю числа.
Применение дополнительного кода позволяет выполнить операцию алгебраического суммирования и вычитания на обычном сумматоре. При этом не требуется определения модуля и знака числа.
Прямой код представляет собой одинаковое представление значимой части числа для положительных и отрицательных чисел и отличается только знаковым битом. В прямом коде число 0 имеет два представления «+0» и «–0».
Обратный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется из прямого кода положительного числа путем инвертирования всех значащих разрядов прямого кода. В обратном коде число 0 также имеет два представления «+0» и «–0».
Дополнительный код для положительных чисел имеет тот же вид, что и прямой код, а для отрицательных чисел образуется путем прибавления 1 к обратному коду. Добавление 1 к обратному коду числа 0 дает единое представление числа 0 в дополнительном коде. Однако это приводит к асимметрии диапазонов представления чисел относительно нуля.
Так, в восьмиразрядном представлении диапазон изменения чисел с учетом знака.
Таблица прямого, обратного и дополнительного кода 4-битных чисел. Для наглядности представления всего диапазона чисел примем, что сетка представления чисел 4-разрядная, где старший разряд (3) — знаковый, а 0-2 разряды содержат значение числа.
| Число | Прямой код | Обратный код | Дополнительный код |
| -8 | — | — | 1000 |
| -7 | 1111 | 1000 | 1001 |
| -6 | 1110 | 1001 | 1010 |
| -5 | 1101 | 1010 | 1011 |
| -4 | 1100 | 1011 | 1100 |
| -3 | 1011 | 1100 | 1101 |
| -2 | 1010 | 1101 | 1110 |
| -1 | 1001 | 1110 | 1111 |
| 0 0 | 1000 0000 | 1111 0000 | 0000 |
| 1 | 0001 | 0001 | 0001 |
| 2 | 0010 | 0010 | 0010 |
| 3 | 0011 | 0011 | 0011 |
| 4 | 0100 | 0100 | 0100 |
| 5 | 0101 | 0101 | 0101 |
| 6 | 0110 | 0110 | 0110 |
| 7 | 0111 | 0111 | 0111 |




