Наиболее важной для практики оказывается ситуация, когда,т.е. для представления кодов в линии связи используется лишь два типа сигналов — технически это наиболее просто реализуемый вариант (например, существование напряжения в проводе (будем называть это импульсом) или его отсутствие (пауза); наличие или отсутствие заряда в ячейке электронной памяти); подобное кодирование называется двоичным. Знаки двоичного алфавита принято обозначать «0» и «1», но нужно воспринимать их как буквы, а не цифры. Удобство двоичных кодов и в том, что при равных длительностях и вероятностях каждый элементарный сигнал (0 или 1) несет в себе 1 бит информации (log2 M = 1); тогда из (3)
и первая теорема Шеннона получает следующую интерпретацию:
Применение формулы (4) для двоичных сообщений источника без памяти при кодировании знаками равной вероятности дает:
При декодировании двоичных сообщений возникает проблема выделения из потока сигналов (последовательности импульсов и пауз) кодовых слов (групп элементарных сигналов), соответствующих отдельным знакам первичного алфавита. При этом приемное устройство фиксирует интенсивность и длительность сигналов, а также может соотносить некоторую последовательность сигналов с эталонной (таблицей кодов).
Возможны следующие особенности вторичного алфавита, используемого при кодировании:
· элементарные сигналы (0 и 1) могут иметь одинаковые длительности (τ0=τ1) или разные (τ0 ≠ τ1);
· длина кода может быть одинаковой для всех знаков первичного алфавита (в этом случае код называется равномерным) или же коды разных знаков первичного алфавита могут иметь различную длину (неравномерный код);
· коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).
Комбинации перечисленных особенностей определяют основу конкретного способа кодирования, однако, даже при одинаковой основе возможны различные варианты построения кодов, отличающихся своей эффективностью.
Помехоустойчивость двоичных неизбыточных кодов.
Кодовые комбинации состоят из условных единиц и нулей. При искажениях в кодовых комбинациях 1 может быть подавлена помехой и перейти в 0. Это означает, что сигнал 1 трансформировался в 0. Вероятность перехода 1® 0 обозначается как  (вероятность трансформации 1 в 0). Вероятность ложного сигнала, т.е. перехода 0 в 1, возможна, если помеха возникает при отсутствии сигнала, т.е. когда посланный 0 трансформируется в 1 и обозначается
(вероятность трансформации 1 в 0). Вероятность ложного сигнала, т.е. перехода 0 в 1, возможна, если помеха возникает при отсутствии сигнала, т.е. когда посланный 0 трансформируется в 1 и обозначается  .
.
Теория вероятностей | Математика TutorOnline
Таким образом, возможны два варианта передачи:
– правильная передача – при этом 1 переходит в 1, т.е.  , а 0 переходит в 0, т.е.
, а 0 переходит в 0, т.е.  или
или  и
и 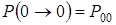 ;
;
– неправильная передача – при этом 1 переходит в 0, т.е.  , или 0 переходит в 1, т.е.
, или 0 переходит в 1, т.е.  , или
, или  и
и  .
.
Вероятность правильной и неправильной передачи 1 и соответственно 0 определяется в соответствии с теоремой о полной группе событий

, (3.17)

. (3.18)
Если  , то образуется симметричный канал, т.е. в симметричном канале
, то образуется симметричный канал, т.е. в симметричном канале  и
и  равны между собой.
равны между собой.
При проектировании эти вероятности задаются:

– если состояние канала хорошее, то ,

– если плохое, то или определяются при испытаниях.
При передаче двоичными неизбыточными кодами возможно два случая:

– передача без ошибок, т.е. все сообщения переданы правильно и оцениваются вероятностью правильного приёма ;

– передача с искажениями хотя бы одного элемента, которая оценивается вероятностью ошибки .
Вероятности  и
и  образуют полную группу сообщений, т.е.
образуют полную группу сообщений, т.е.

. (3.19)
При расчётах  и
и  придерживаются следующих положений из теории вероятностей:
придерживаются следующих положений из теории вероятностей:
– если в двоичном канале заданы вероятности двух переходов, то вероятности двух других переходов могут быть найдены на основе теоремы о полной группе событий (3.17) и (3.18);
– вероятность того, что одна комбинация перейдёт в другую, равна произведению вероятностей переходов каждого символа.
Например, передана комбинация 11001. Под воздействием помех эта комбинация исказится так, что будет вместо неё принята комбинация 10011.
Определим, какова вероятность трансформации первой кодовой комбинации во вторую, если  и
и  известны.
известны.
Для такой трансформации необходимо, чтобы во втором элементарном сигнале произошла ошибка типа 1 ® 0, а в четвёртом 0 ® 1. Все остальные элементы должны быть приняты верно. Согласно теореме умножения

.
Учитывая, что  и
и  , получим
, получим

.
Таким образом может быть определён любой член матрицы вероятностей трансформации.

, (3.20)

где – число трансформации вида 0®1;

– число трансформации вида 1®0;

– число совпадающих единиц;
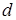
– число совпадающих нулей;
a+b+c+d – число разрядов кодовой комбинации.
Определим условную вероятность правильной передачи. Для правильной передачи кодовой комбинации необходимо, чтобы были правильно переданы все её элементы.

Пусть комбинация состоит из нулей и m единиц. Тогда

. (3.21)

В частном случае для симметричного канала, когда ,
 при
при  , (3.22)
, (3.22)

где – число элементарных сигналов;

– вероятность ошибочной передачи одного элементарного сигнала.
Вероятность любой ошибки при передачи i –й комбинации равна

.
Для симметричного канала

. (3.23)
Если имеется  сообщений, то вероятность трансформации любого i- го сообщения в любое
сообщений, то вероятность трансформации любого i- го сообщения в любое  — е сообщение, где
— е сообщение, где  , определяется выражением
, определяется выражением

. (3.24)
Для оценки помехоустойчивости необходимо знать вероятности передачи каждого сообщения  и все условные вероятности трансформации одних сообщений в другие
и все условные вероятности трансформации одних сообщений в другие  , задаваемые обычно в виде матрицы вероятностей трансформации.
, задаваемые обычно в виде матрицы вероятностей трансформации.

. (3.25)
Вероятность возникновения ошибки при передаче i–го сообщения равна

. (3.26)
Средняя вероятность ошибки за такт (время, в течение которого осуществляется передача всех сообщений) найдётся усреднением условных вероятностей ошибки по всем сообщениям с учётом вероятности их передачи

. (3.27)
Пример 3.3. Найти вероятность возникновения двух или трёх ошибок при передаче кодовой комбинации  , если
, если  и
и  .
.

Решение. При двух ошибках возможно типов искажений:
Б – 1001, В – 1100, Г – 0110, Д – 0011, Е – 1010, Ж – 0101.
Тогда вероятность возникновения двух ошибок Р (2)= Р (А®Б)+ Р (А®В)+ + Р (А®Г) + Р (А®Д) + Р (А®Е) + Р (А®Ж)= Р 11 Р 10 Р 10 Р 11 + Р 11 Р 11 Р 10 Р 10 + Р 10 ´ ´ Р 11 Р 11 Р 10+ Р 10 Р 10 Р 11 Р 11+ Р 11 Р 10 Р 11 Р 10 + Р 11 Р 10 Р 11 Р 10 Р 11 = 6 Р 11 Р 11 Р 10 Р 10 = = 6 Р 11 2 Р 10 2 = 6(1– Р 10) 2 Р 10 2 » 6·10 –6 .

При трёх ошибках возможно типа искажений: З- 1000,
И – 0100, К – 0010, Л – 0001.

Тогда вероятность возникновения трёх ошибок P (З) = Р (А ® З) + Р (А ® И) +
+ Р (А ® К) + Р (А ® Л) .
Таким образом, вероятность возникновения трёх ошибок существенно меньше вероятности возникновения двух ошибок.
Пример 3.4. Определить вероятность правильного приёма и вероятность любой ошибки в простом двоичном коде с  при передаче по симметричному каналу с
при передаче по симметричному каналу с  .
.
Решение. В соответствии с выражением (3.22) вероятность правильного приёма  .Вероятность возникновения любой из ошибок согласно (3.23)
.Вероятность возникновения любой из ошибок согласно (3.23) 
Экзаменационный билет № 31
Ваш браузер не поддерживается
Интернет-сервис Студворк построен на передовых, современных технологиях и не может гарантировать полную поддержку текущего браузера.

Установить новый браузер
- Google Chrome

Скачать
Яндекс Браузер

Скачать
Opera

Скачать
Firefox

Скачать
Microsoft Edge
Нажимая на эту кнопку, вы соглашаетесь с тем, что сайт в вашем браузере может отображаться некорректно. Связаться с техподдержкой
Работаем по будням с 8.00 до 18.00 по МСК
На любой из позиций импульсного кода могут быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс)
На любой из позиций импульсного кода могут быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехами «1» преобразуется в «0» с вероятностью 0,02 и «0» в «1» с вероятностью 0,04. Найти вероятность приёма «0» на конкретной позиции кода. Найти вероятность того что был передан «0», если принят «0».
Решение
Потяни, чтобы посмотреть
B1 — был передан ноль
B2 — была передана единица
P(B1)= 0.5
P(B2)= 0.5
событие A — принят ноль
PB1(A)= 1- 0.02= 0.98 — ноль принят при переданном нуле
PB2(A)= 0.04 — ноль принят при переданной единице
Вероятность приема нуля
P(A)= P(B1)*PB1(A)+ P(B2)*PB2(A)= 0.5*0.98+ 0.5*0.04= 0.51
Вероятность того, что был передан 0, если принят 0
PA(B1)= P(B1)*PB1(A) / P(A)= 0.5*0.98 / 0.51= 0.96078
50% задачи недоступно для прочтения
Полное решение в Кампус. Переходи в личный кабинет по кнопке и получи решение за 1 токен, в формате PDF
Контрольная Информатика, 7 задач, номер: 194038

Информатика, 7 задач marvel7 , 1) На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехи преобра.
Информатика, 7 задач
1) На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехи преобра.
144010 , Россия , Московская , Электросталь , ул.Ялагина, д. 15А
StudentEssay

КУПИТЬ ЭТУ РАБОТУ.
1) На любой из позиций двоичного кода может быть с равной вероятностью переданы «0» (отсутствие импульса) и «1» (импульс). Помехи преобразуют «1» в «0» с вероятностью 0,02 и «0» в «1» с вероятностью 0,04. Найти вероятность приема «0» на конкретной позиции кода. Определить вероятность того, что был передан «0», если принят «0».
2) В алфавите племени БУМ всего 4 буквы (А, У, М, Б), один знак препинания (.) и для разделения слов используется пробел. Подсчитали, что в популярном романе «МУБА» содержится 10000 знаков, из них: букв А – 4000, букв У – 1000, букв М – 2000, букв Б – 1500, точек – 500, пробелов – 1000. Найти энтропию книги
3) Определить энтропию источника сообщений, передаваемых по каналу связи, и состоящих из равновероятных символов, если влияние помех в канале описывается матрицей
P(y/x)=0,96 0,04 0
0,03 0,95 0,02
0,02 0,04 0,94
4) Вероятности появления символов источника алфавита p(x1)=0,5, p(x2)= 0,25, p(x3)=0,125, p(x4)=0,125. Между соседними символами имеются корреляционные связи, которые описываются матрицей вероятностей
13/16 3/16 0 0
1/8 ? 3/8 0
0 0 0 1
? ? ? 0
Требуется определить избыточность источника при статистической независимости символов и избыточность при зависимости символов.
5) Источник сообщений выдает целые значения xi (i=1…12) случайной величины Х, распределение которой подчиняется закону Пуассона с параметром а=3. Закодировать сообщение методом Шенно-Фано. Определить: 1) Пригодность кода для передачи сообщений в смысле их однозначного кодирования; 2) На сколько код Шенно-Фано длиннее оптимального (в %)
6) Сообщение с символами х1, х2, х3, х4 передается по дискретному двоичному каналу с соответствующими вероятностями 0,1, 0,2, 0,2, 0,2, 0,3. Полоса пропускания канала обеспечивает возможность передачи двоичных символов с длительностью t=10-4сек. Требуется выбрать наилучший способ кодирования и декодировать произвольное двоичное сообщение, определить скорость передачи информации при каждом из способов кодирования и сравнить ее с пропускной способностью канала
7) Пользуясь кодом Хэмминга найти ошибку в сообщении 1111 1011 0010 1100 1101 1100 110.
Сообщения источника, заданного распределением вероятностей . кодируется словами: , ,,
соответственно. Необходимо найти вероятность появления единицы в
первой позиции кодового слова при условии, что во второй позиции
кодового слова появилась единица; вероятность появления нуля во второй
позиции кодового слова при условии, что в первой позиции кодового слова
появился нуль; вероятность появления сообщения х2 при условии, что в
первой позиции кодового слова появился нуль. Исходные данные:
P1 = 0,2 + 0,005 • N:
P2 = 0,3 — 0,005 • N;
P3 = 0,1 +0,01 • N:
P4 = 0,4 – 0,01 • N.
2. На любой из позиций двоичного кода может быть сравной
вероятностью переданы «0» (отсутствие импульса) и «1» (импульс).
Помехи преобразуют «1» в «0» с вероятностью 0,02 и «0» в «1» с
вероятностью 0,04, Найти вероятность приема «0» на конкретной позиции
кода. Определить вероятность того, что был передан «0», если принят «0».
3. По линии связи посылаются сигналы 1,0 с вероятностями р1 = 0.6,
р0= 0.4. Если посылается сигнал 1, то с вероятностями r11=0.9, r10 = 0,1
принимаются сигналы 1, 0. Если посылается сигнал 0, то с вероятностями r01=0.3, r00=0.7 принимаются сигналы 1, 0, Какова условная вероятность того, что посылается сигнал 1 при условии, что принимается сигнал 1?
1. Для нахождения вероятности появления единицы в первой позиции кодового слова при условии, что во второй позиции кодового слова появилась единица, нам необходимо воспользоваться формулой для условной вероятности:
P(первая позиция = 1 | вторая позиция = 1) = P(первая позиция = 1 и вторая позиция = 1) / P(вторая позиция = 1)
Так как мы уже знаем вероятности сообщений источника, заданного распределением вероятностей , мы можем заменить значения в формуле:
P(первая позиция = 1 | вторая позиция = 1) = P(х1) / (P(х1) + P(х3))
Значения P(х1) и P(х3) можно найти, заменив соответствующие вероятности из исходных данных:
P(х1) = P1 = 0,2 + 0,005 • N,
P(х3) = P3 = 0,1 +0,01 • N.
Итак, мы получаем:
P(первая позиция = 1 | вторая позиция = 1) = (0,2 + 0,005 • N) / (0,2 + 0,005 • N + 0,1 +0,01 • N).
2. Для нахождения вероятности приема «0» на конкретной позиции кода, при условии, что был передан «0», мы снова используем формулу для условной вероятности:
P(передан «0» | принят «0») = P(передан «0» и принят «0») / P(принят «0»).
В данном случае, нам нужно найти вероятность приема «0» при условии, что был передан «0», а вероятность помехи составляет 0,04 (т.е. вероятность обратной ошибки). Следовательно, вероятность принятого «0» равна 0,04, а вероятность приема «0» и передачи «0» равна 1 — 0,04 = 0,96.
Таким образом, мы получаем:
P(передан «0» | принят «0») = 0,96 / 0,04 = 24.
3. Для нахождения условной вероятности того, что посылаемый сигнал равен 1 при условии принятого сигнала равного 1, мы используем формулу для условной вероятности:
P(посылается сигнал 1 | принимается сигнал 1) = P(посылается сигнал 1 и принимается сигнал 1) / P(принимается сигнал 1).
В данном случае, нам нужно найти вероятность посылки сигнала 1 при условии, что принят сигнал 1. Для этого мы можем использовать соответствующие вероятности из исходных данных:
P(посылается сигнал 1) = р1 = 0.6,
P(принимается сигнал 1) = P(принимается сигнал 1 | посылается сигнал 1) • P(посылается сигнал 1) + P(принимается сигнал 1 | посылается сигнал 0) • P(посылается сигнал 0),
P(принимается сигнал 1 | посылается сигнал 1) = r11 = 0.9,
P(принимается сигнал 1 | посылается сигнал 0) = r01 = 0.3.
Таким образом, мы получаем:
P(посылается сигнал 1 | принимается сигнал 1) = (0.9 • 0.6) / ((0.9 • 0.6) + (0.3 • 0.4)).
Вот ответы на поставленные вопросы. Пожалуйста, если у вас возникнут какие-либо вопросы, не стесняйтесь задавать их. Я готов помочь!
Ответы на экзаменационные вопросы № 1-14 по дисциплине «Теория информации» (Информация, сообщение, сигнал, помеха. Неравенство Крафта. Алгоритм Хаффмана) , страница 2

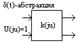
Реакция любого элемента системы передачи (4х-полюсника) на дельта-импульс называется его импульсной характеристикой: 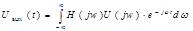

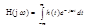
Импульсная характеристика полностью характеризует элемент во временной функции:



Если удалось подобрать такой импульс, который в диапазоне частот имеет неизменную форму, то это δ-импульс.



Прохождение сигнала


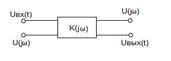
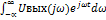
2)Uвых(t)=1/2π

-интеграл свертки
Сигнал на выходе равен сигналу свертки между u(t) и h(t-τ) cдвинутым на время τ
6.Дискретизация непрерывных сигналов.Теорема Котельникова.Виды погрешностей.Практическое значение теоремы.
Сущность дискретизации заключается в том, что непрерывность во времени функции s(t) заменяется последовательностью коротких импульсов,
Шаг дискретизации должен быть таким, чтобы было возможно восстановление непрерывной функции по ее отсчетам с допустимой точностью
Теорема: если любой непрерывный сигнал u(t)не содержит частотных составляющих выше частоты F, то он полностью определяется своими отсчетами взятыми через интервалы времени дискретизации Т=1/2F; любой непрерывный сигнал с ограниченным спектром может быть восстановлен по своим отсчетам с помощью ряда Котельникова.


–ряд Котельникова является дискретным аналогом интеграла свертки.
Погрешности при восстановлении ряда К.:
1)восстановление ведется по конечному числу отсчетов
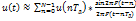

2)Восстановление не по точным, а по приближенным отсчетам

3)tnTд ,необходимо обеспечить равенство.
4)восстановление ведется по приближенной ф-ии вида sinx/x
можно справится со всеми погр., кроме 1)
значение: временное разделение каналов(временное уплотнение), можно обеспечить по одной цепи несколько каналов.
7.Геометрическое представление сигналов: пространство Евклида и пр-во Гильберта, понятие расстояния, нормы. Энергия и норма прямоугольного импульса.
Для описания дискретных сигналов — пр-во Евклида(R 2 );для непрерывных – Гильберта(L 2 )
В математике длину вектора называют его нормой.Пространство называется нормированным если любому вектору однозначно соответствует норма. Во всех функциональных пр-вах определяющим является понятие расстояния. Метрика-правило, по которому задается расстояние.
в пр-вах Е и Г метрику определяют через скалярное произведение векторов.
норма-длина вектора от начала координат, до заданной точки
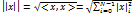
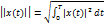
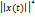
–энергия сигнала x(t)-напряжение или ток, измеряемые на сопротивлении в 1 Ом мощность сигнала:

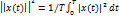

;

8.Непрерывные сигналы как случайные стационарные процессы. Вероятностные, частотные и временные характеристики случайных сигналов. Теорема Хинчина-Винера
Случайный процесс (стохастический) – это случайная функция времени, которая в любой момент принимает различные значения, подчиняющиеся определенному закону распределения.
Стационарные – процесс, вероятностные характеристики которого не меняются во времени. ->Эргодические – стационарный случайный процесс, вероятностные характеристики которого не зависят от того как они получены.
Не стационарные – меняются.
Гауссовские – нормальное распределение, не гауссовские.
Если наблюдается зависимость от нескольких переменных, (частота, фаза и тд) – это случайное поле.
Вероятностные характеристики (моментные функции):

1) — среднее значение сигнала (пост. сост.)
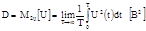
2) — характеризует разброс значений (или ср. мощность случ. процесса)
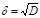
3) — действительное знач. напр. случайного процесса.
4)  — ф-ция автокорреляции, при
— ф-ция автокорреляции, при 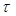 =0 это дисперсия.
=0 это дисперсия.
Временные и частотные характеристики сл. процессов
У сл. процесса мы не можем задать аналитически U(t).
U(t)->U(jw) – спектральная плотность; U(w,t)
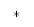
Текущий спектр – ограничивает интервал, получая решение в данный момент.

Теорема Хинчина-Винера.

Для стационарных случайных процессов можно определить усреднённую за некоторое время t спектральную плотность мощности:
Таким образом:Теорема Х.-В.:
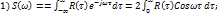
(спектр мощности)
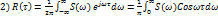
(функция автокорреляции – можем предсказать сл. Процесс)
9.Определение вероятности превышения амплитудой нормально распределенной помехи заданного порога.
10.Определение вероятности ошибки при передаче импульсов постоянного тока в смеси с аддитивной нормально распределенной помехой.
11.Типы дискретных источников информации, их характеристики. Количество информации в букве сообщения при равновероятности и взаимной независимости букв.Единицы количества информации
Сущ. 3 типа дискретных источников информации:
1)с равной вероятностью и взаимной независимостью появления букв
2)с неравной вероятностью и взаимной независимостью
3)с неравной вероятностью и взаимозависимостью(марковские)
алфавит 1, a2, …aN>;вероятность появления буквы р(аi); скорость передачи буквы(буква /ед.времени);энтропия(кол-во информации) Н(А)=[бит/букву];производительность-суммарная энтропия сообщений, переданных за единицу времени (бит/е.в.)
Единицы кол-ва информации: бит/букву
Бит — это двоичный логарифм вероятности равновероятных событий;базовая единица измерения количества информации, равная количеству информации, содержащемуся в опыте, имеющем два равновероятных исхода
12. Количество информации в букве сообщения при неравной вероятности и взаимной независимости букв. Мера кол-ва информации.
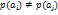
— неравновероятность

– взаимонезависимость появления букв
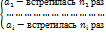
n —
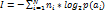
-кол-во информ. в n-букв.сообщении

–среднее кол-во информации
Мера кол-ва информации- энтропия
17.N-уровневый симметричный канал и его пропускная способность. Каналы с независимыми ошибками и пакетами ошибок. Распределение вероятности ошибки в канале с независимыми ошибками.

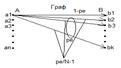 N-уровневый симметричный канал -два двоичных импульса кодируются одним
N-уровневый симметричный канал -два двоичных импульса кодируются одним
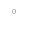
00 → -1B
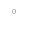
11 → +3B
p(ai) = 1/N; C=max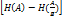 ; Hmax =
; Hmax = 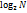
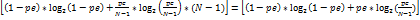
H(A/B) = —
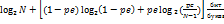
C=
Каналы с независимыми ошибками
Если ошибки распределены равномерно и каждая последующая не зависит от предыдущей-то канал с незав. ошибками.
 |
 |
pk= Cn k pe k (1- pe) n — k подчиняется биномиальному распределению(закон Бернулли)
для описания используются цепи маркова метод перемежения данных-позволяет избавится от действия пакета ошибок(передают по столбцам).чем больше коэффициент перемежения тем лучше










 |
 |
13.Количество информации в букве сообщения при неравной вероятности и взаимозависимости букв.
энтропия марковского источника.
источник задается:1)матрицей условных вероятностей;






