Поскольку одно и тоже число может быть записано в различных системах счисления, встает вопрос о переводе представления числа из одной системы (p) в другую (q). Будем обозначать такое представление Ap®Aq. Теоретически можно произвести перевод для любых p и q. Однако подобный прямой перевод будет затруднен тем, что придется выполнять операции по правилам арифметики не десятичных систем счисления. По этой причине более удобным можно считать вариант преобразования с промежуточным переводом Ap®Ar®Aq с основанием r, для которого арифметические операции выполнить легко. Такими удобными основаниями являются r=1 и r=10, т.е. перевод осуществляется через унарную или десятичную систему счисления.
Идея алгоритма перевода следующая: положим начальное значение Aq=0. Из числа ap вычтем единицу по правилам вычитания системы p и добавим ее к Aq по правилам сложения системы q; будем выполнять эту последовательность действий пока не достигнем Aр=0.
Выполнить преобразование 223®А6.
Последовательность действий и промежуточные результаты для наглядности представим в виде следующей таблицы:
| Шаг |
| А3 – 1 |
| А6 + 1 |
Очевидно, первая и вторая части преобразования не связаны друг с другом, т.о. можно рассматривать их по отдельности.
Поскольку А10 целое десятичное число в его разложении отсутствуют коэффициенты с отрицательными индексами и его можно представить в виде.
A10 = a n-1×q n-1 + a n-2× q n-2 + … + a 2×q 2 + a 1×q 1 + a 0 q 0 .
Разделим число А10 на q. Частное будет равно
а остаток будет равен a 0.
Полученное неполное частное опять разделим на q, остаток от деления будет равен а 1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр
a 0, a 1, a 2,…, a n-1,которые входят в q-ичное представление числа А10 и совпадают с остатками при последовательном делении данного числа на q. Но мы их получили в порядке, обратном порядку расположения в q-ичном представлении числа А.
Рассмотренную выше последовательность действий удобнее изображать следующим образом:
2 3 1
1
Записывая остатки от деления в обратном направлении получим число 1123.
Данное преобразование явно вытекает из формулы (1): если все слагаемые в развернутой форме не десятичного числа представить в десятичной системе и вычислить полученное выражение по правилам десятичной арифметики, то получится число в десятичной системе равной данному (это правило распространяется как на целые, так и на дробные числа).
1123 = 1*10 2 +1*10 1 +2*10 0 = 1*3 2 +1*3 1 +2*3 0 =1410
1001012 = 1*10 101 +0*10 100 +0*10 11 +1*10 10 +0*10 1 +1*10 0 =1*2 5 +0*2 4 +0*2 3 +1*2 2 +0*2 1 +1*2 0 =3710
Урок 32. Перевод чисел между системами счисления
14FC16 = 1*10 3 +4*10 2 +F*10 1 +C*10 0 =1*16 3 +4*16 2 +15*16 1 +12*16 0 =537210
101,012 = 1*10 10 +0*10 1 +1*10 0 +0*10 -1 +1*10 -10 =1*2 2 +0*2 1 +1*2 0 +0*2 -1 +1*2 -2 =5,2510
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Готовимся к ЕГЭ. 1.1. Системы счисления. Теория.
Первая часть разбора теории о системах счисления. Общие понятия.
Опрос в группе ВК.
Если вы желаете поддержать автора курса
Яндекс.Деньги
https://money.yandex.ru/to/410011285238281
WebMoney
R216678734285
Текст видео.
В этом видеоуроке мы поговорим о системах счисления.
Для начала определимся с основными понятиями темы.
Ключевое определение – системы счисления. Системой счисления можно назвать способ записи чисел с помощью символов и правила выполнения операций над этими числами.
Системы счисления характеризует алфавит – это набор символов, используемый в данной системе счисления. Один отдельный символ называется цифрой. А составленное из цифр значение, или величина, называется числом. Если провести аналогию с литературой, то цифра – это буква, а число – это слово. Как слова могут состоять из одной буквы, так и числа тоже могут состоять из одной цифры. Только числа нам нужны для обозначения некоторого количества, а цифры – чтобы записать числа. Количество цифр в алфавите системы счисления также называют мощностью, хотя это определение больше применимо к тексту, нежели к системам счисления.
Следующая характеристика систем счисления – это основание. Основание равно количеству цифр в данной системе счисления.
Система счисления отвечает на два вопроса: как записать число в этой системе счисления, и как выполнять арифметические операции, т.е. сложение, вычитание, умножение и деление.
Надо понимать следующее: количество чего-либо (птиц за окном, волос у человека, и т.д.) – это некоторое абстрактное множество. И как записать это количество, и определяет система счисления. Мы с вами всю жизнь пользуемся десятичной системой счисления. В ней используется 10 цифр – от 0 до 9. Википедия говорит, что ее использование связано с тем, что у человека 10 пальцев на руках, а одним из первых инструментов, которые мы начинаем использовать для расчетов, являются именно пальцы. Недаром есть выражение “объяснить на пальцах”. Но в нашей жизни есть следы других систем счисления, которые использовали разные народы в древние времена. У нас 12 месяцев, 12 часов, 7 дней недели. Это не вписывается в привычный нам мир десяток.
Кроме десятичной системы счисления некоторое распространение имеет римская. Эти системы счисления (римская и десятичная) относятся к разным типам. Десятичная – это позиционная, а римская – непозиционная система счисления.
В позиционных системах счисления позиция цифры в числе влияет на ее значение. А в непозиционных, соответственно, нет.
Отличия между ними легко продемонстрировать на следующем примере. Рассмотрим два числа, записанные в десятичной и в римской системах счисления. Это числа 111 и III. И то, и другое выглядят как три единицы, идущие подряд. Но количественное значение у них абсолютно разное.
Рассмотрим на примере несколько систем счисления.
Название системы счисления, как правило, отражает ее основание. А алфавит всегда начинается с нуля.
В двоичной системе счисления основание равно двум, и, соответственно, две цифры – 0 и 1. В пятеричной основание 5, а алфавит идет с нуля и до 4. Вообще, прослеживается четкая закономерность: максимально возможная цифра в системе счисления меньше основания на единицу.
В используемой нами системе счисления максимальная цифра это 9. И тут все, большей цифры мы не знаем, поскольку арабские цифры заканчиваются именно девяткой. Поэтому, если возникает необходимость записать одной цифрой большее значение, решили использовать буквы. Так, в шестнадцатеричной системе счисления максимальная цифра – это F. А означает она 15. Таким образом, одно и тоже количество можно записать совершенно по-разному. Например, число 10 в перечисленных системах счисления выглядит так:
Нижним индексом указывается основание системы счисления. Почему все эти значения равны, мы узнаем чуть позже. Пока надо понимать, что одно и тоже количество может быть записано по-разному, в зависимости от того, в какой системе счисления мы его указываем.
Школьный курс информатики подразумевает изучение определенных аспектов этой темы. Для подготовки к экзамену необходимо знать их все. Краткий теоретический экскурс по теме я уже провел. Обязательно надо уметь переводить числа из любой системы счисления в другую. Выполнять арифметические операции в разных системах счисления. Конечно, можно свести эту задачу к предыдущей. Мы можем перевести в десятичную, выполнить действия в ней, это мы прекрасно умеем, а ответ перевести туда, куда нужно. Но это далеко не всегда рационально, и может занять гораздо больше времени, чем требуется для решения определенного задания. Так что мое мнение таково: необходимо уметь выполнять арифметические операции во всех системах счисления. Так же обязательно надо понимать, как числа записываются в память компьютера: целые, вещественные, без знака или со знаком. Ну и, наконец, есть определенные закономерности, которые позволяют сводить решение некоторых заданий к вполне тривиальным вещам.
Понятие о системах счисления
Число — это абстрактное математическое понятие. Чтобы работать с числа-ми практически, каждое число нужно обозначить. Принцип, в соответствии с которым определяются обозначения, называется системой счисления.
Счисление (мат.энцикл.), нумерация – совокупность приемов представления натуральных чисел. В любой системе счисления некоторые символы служат для обозначения определенных чисел, называемых узловыми. Остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел. Системы счисления различаются выбором узловых чисел и способами образования алгоритмических.
Пример. Одно и то же число может быть записано в разных системах счисления. Например, «19» и «XIX» — две записи одного и того же числа.
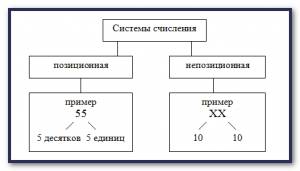
Система счисления называется непозиционной, если каждый числовой знак в записи любого числа в ней имеет одно и тоже значение. Если же значение числового знака зависит от его расположения в записи числа, то система называется позиционной.
Пример. Десятичная система исчисления¬¬- позиционная, римская система исчисления — непозиционная.
Основание позиционной системы счисления — это число, показывающее, во сколько раз отличается значение одной и той же цифры в соседних разрядах. Количество цифр, используемых в позиционной системе счисления, равно основанию этой системы.
Пример. Рассмотрим число 55, записанное в десятичной системе. В соседних разрядах находятся одинаковые цифры, однако одна из них обозначает 5 (пять единиц), а другая — 50 (пять десятков). 50/5 =10 , что и равняется основанию десятичной системы счисления.
Пример. В десятичной системе счисления 10 цифр: 0, 1, . , 9.
Примечание. Если число записано не в десятичной системе счисления, то обозначают систему нижним индексом, например: 4058 , 1001102 .
Системы счисления
1. Система счисления – это …
1) Правила выполнения операций над числами
2) Правила записи чисел
3) 1 и 2
4) нет верного ответа
2. Если в записи чисел могут быть использованы только цифры 0 1 2 3 4 5 6 7, то такая система счисления называется …
1) Двоичной
2) Семеричной
3) Восьмеричной
4) Нет верного ответа
3. Укажите те системы счисления, в которых НЕ МОЖЕТ быть число 501
1) Десятичная
2) Двоичная
3) Восьмеричная
4) Шестнадцатеричная
4. Как называется система счисления, в которой значение цифры зависит от занимаемой ею позиции в числе?
1) позиционная;
2) непозиционная;
3) нет верного ответа;
4) перечисленное в п.1-2.
5. Можно ли одно и тоже число записать в разных системах счисления?
1) Да
2) Нет
6. Если в записи чисел могут быть использованы только цифры 0,1,2, то такая система счисления называется
1) двоичная
2) троичная
3) семиричная
4) восьмиричная
7. В какой системе счисления, кроме цифр используются буквы латинскоко алфавита?
1) двоичной
2) восьмеричной
3) десятичной
4) шестнадцатиричной
8. В двоичной системе счисления основание системы
1) 1
2) 2
3) 10
4) 16
9. Недостатком непозиционной системы счисления является
1) сложно выполнять арифметические операции
2) удобное представление дробных и отрицательных чисел
3) для записи больших чисел не требуется постоянно вводить новые знаки
10. Цифры – это
1) символы, участвующие в записи числа
2) буквы, участвующие в записи числа
3) пиктограммы, участвующие в записи числа
Заметили ош Ы бку
Выделите текст и нажмите Ctrl+Enter
Перевод чисел из двоичной системы счисления в десятичную
В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:
5476 = 5000 + 400 + 70 + 6
Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:
5476 = 5 * 10 3 + 4 * 10 2 + 7 * 10 1 + 6 * 10 0
После равенства числа 5, 4, 7 и 6 – это набор цифр из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10 (1-1) . Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:
10001001 = 1 * 2 7 + 0 * 2 6 + 0 * 2 5 + 0 * 2 4 + 1 * 2 3 + 0 * 2 2 + 0 * 2 1 + 1 * 2 0
Результат вычислений дает десятичное число, количественно равное двоичному 10001001:
1*2 7 + 0*2 6 + 0*2 5 + 0*2 4 + 1*2 3 + 0*2 2 + 0*2 1 + 1*2 0 =
= 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык современной вычислительной техники.
Когда любые данные сохраняются на компьютере, они кодируются числами. С числами же компьютер выполняет операции, изменяя эти данные.
Допустим, у нас есть десятичное число 14, которое требуется сохранить в компьютерной памяти. Мы задействуем участок памяти, в данном случае состоящий как минимум из двух элементов, отводимых под разряды. В одном из разрядов мы сохраняем десятичное число 1, в другом – число 4.
Элемент памяти – это физическое устройство. Если проектировать его для хранения десятичной цифры, потребуется создать такое устройство, которое может находиться в десяти разных физических состояниях и способно переключаться между ними. Каждое из этих состояний будет соответствовать числу от 0 до 9.
Создать такой элемент памяти возможно, однако сложнее и дороже, чем создать элемент, способный находиться только в двух состояниях. Одно состояние сопоставить нулю, второе – единице. Кроме того, подобное хранение данных является более надежным.
Поэтому оказалось проще перевести число 14 в двоичную систему счисления, получив число 1110, и именно его сохранить в памяти. И пусть даже при этом будут задействованы не два, а четыре разряда, то есть четыре элементарных единиц памяти.
Сравнение систем
СС могут быть с произвольной основой, но популярны 2,8,10,16-ые.
Сравнительная таблица разных систем счисления:

Перевод числа 75 в разные системы:
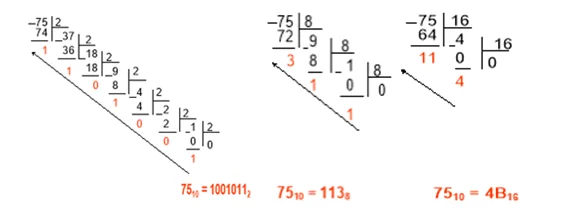

Источник
Правила перевода из двоичной, восьмеричной и шестнадцатеричной в 10СС:
Исходный вариант следует разделить на тройки цифр, с крайней справа. Если не хватает, старший разряд дополнить 0. Далее под каждой триадой ставится подходящий символ из 8‑ой системы.

Рассмотрим перевод на примере числа 579, которое соответствует 10010000112
001 001 000 011

Правила перевода из двоичной в шестнадцатеричную систему счисления:
Число разбивается по 4 знака, начиная справа (с меньшего разряда). Если не будет хватать символов у старшего разряда, тетраду дополняют нулями.

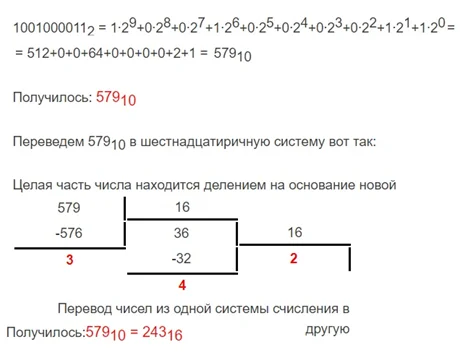
Сравнительный перевод дробей в СС
Чтобы перевести правильные дроби из 10-ой СС в другие позиционные, следует придерживаться правила, которое хорошо видно на примере перевода числа 0,35:
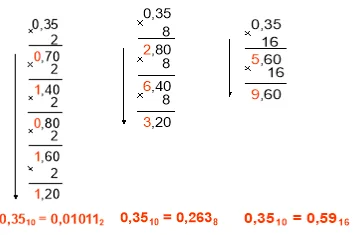
Удобно писать над каждой цифрой порядок, а дальше ее умножить на основу СС в степени разряда.

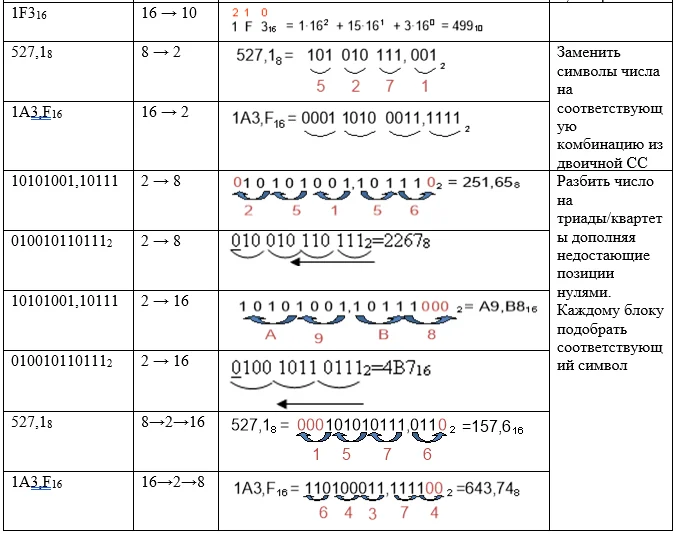
Перевод целых и дробей в 2СС, 8СС, 16СС:

Таблицы истинности
При помощи тех же нулей и единиц создаются таблицы истинности логических выражений, в которых описаны всевозможные варианты.
Основные логические операции

Например, конъюнкция является одной из логических операций. Она является истиной только в том случае, если два высказывания имеют истинные значения.
Логические переменные таблицы истинности обозначают p и q, а их значения выражают при помощи 0 и 1, где 0 – ложь, 1 – истина:

Фрагмент таблицы истинности для конъюнкции.
Так выражаются условия для всех логических операций.
Применяются таблицы истинности еще с начала 20 века в алгебре, логике, программировании.




