Может ли индуктивность быть отрицательной

Содержание

On-line Дневник
https://profiles.google.com/105627930876240192950
10:44 pm November 16th, 2011
Генератор на отрицательной индуктивности

звиняюсь что в эту тему, не совсем про отрицательную индуктивность.
но думаю что для понимания всё же будет интересно прочесть вот это..

————>
Гигантский дипольный резонанс атомных ядер. Коллективные Е1-возбуждения в ядре отвечают колебанию электрического дипольного момента ядра, т.е. колебанию всех протонов относительно всех нейтронов. Не случайно, поэтому, первые попытки интерпретации ГДР были связаны с коллективными моделями. Причем, без детальных расчетов было ясно, что энергия Е1-возбуждений, обусловленных движением всех нуклонов ядра, должна быть во много раз больше, чем энергия поверхностных колебаний ядра.И. М. Капитонов открыл «Закономерность конфигурационного расщепления гигантского дипольного резонанса у лёгких атомных ядер» Создал и читал специальные курсы «Взаимодействие электромагнитного излучения с атомными ядрами», «Взаимодействие фотонов и электронов с атомными ядрами»

PS
то есть я так понимаю что можно сжать и потом будет колебаться, и можно также растянуть орбиты и потом они будут колеблясь сжиматься..
в принципе и в том и в том случае колебания похожие..
но .
при изначальной приложенной энергии система будет для восстановления требовать от среды разные если можно так сказать «потенциалы» ( ??горизонтально- вертикально?? )
может в этом соль?
PPS
блин . сложно всё это.

Понятие взаимной индуктивности

При изменении тока, протекающего через катушку индуктивности, в ней наводится эдс самоиндукции. Для линейной индуктивности справедливо соотношение $ e_ = — L_1 frac , $ где e11 — эдс самоиндукции (двойной индекс «1» означает, что эдс возникает в первой катушке и причиной является изменение тока в ней же); L1 — индуктивность катушки; i1 — ток в катушке (рис. %img:l1).

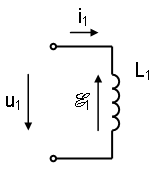
Рис. %img:l1

Кроме того, если катушка L1 имеет магнитную связь с некоторой другой катушкой L2 (т.е. первая катушка находится в магнитном поле второй или, иначе говоря, магнитный поток, создаваемый L2, частично пронизывает L1), то изменения тока в L2 индуцируют эдс в катушке L1: $ e_ = — M_ frac . $ Коэффициент M12 — взаимная индуктивность (или коэффициент взаимной индукции). Взаимная индуктивность является величиной, характеризующей магнитную связь катушек. В данном случае она показывает, насколько сильно изменение тока во второй катушке влияет на эдс, наведённую в первой катушке.

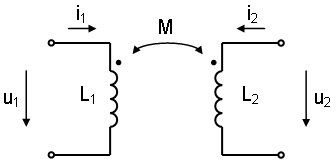
Отрицательная индуктивность

Рис. %img:l1l2

С учётом сказанного, напряжение на L1 может быть выражено как $ u_1 = — (e_+e_) = L_1 frac + M_ frac . $ Аналогичное соотношение справедливо и для L2, а в целом две магнитно связанные индуктивности описываются следующей системой уравнений, всем известной из теории цепей: $ begin u_1 = L_1 frac + M_ frac \ u_2 = M_ frac + L_2 frac . end $ При записи уравнений мы использовали два разных обозначения для коэффициента взаимной индукции, M12 и M21. Однако хорошо известно, что в действительности M12 = M21, т.е. взаимная индуктивность, характеризующая влияние второй катушки на первую, равна взаимной индуктивности, характеризующей влияние первой катушки на вторую. Значит, можно говорить просто о взаимной индуктивности M.

Независимость взаимной индуктивности от перестановки индексов или свойство взаимности часто воспринимается как нечто само собой разумеющееся, приводится просто как факт, без доказательства. Но на самом деле справедливость свойства не столь уж очевидна и требует обоснования.

Далее попробуем выполнить обоснование на основе энергетических соображений. Будем делать это в самом общем виде. В качестве отправной точки возьмём записанную выше систему уравнений, т.е. связанные индуктивности будем рассматривать на уровне теории электрических цепей, отвлечённо от вопросов электродинамики, без учёта каких либо конструктивных особенностей системы.

Но прежде несколько слов об используемом здесь соглашении о знаке M. В то время как индуктивность — всегда положительная величина, в отношении взаимной индуктивности существуют два подхода. Иногда M считают алгебраической величиной, которая может быть как положительной, так и отрицательной. Это бывает удобно, например, если M может изменяться (скажем, если катушки являются подвижными и нужно описать поведение цепи при повороте катушек относительно друг друга). Но чаще всего оказывается более предпочтительным другой подход. При фиксированном значении взаимной индукции, всегда можно выбрать положительные направления токов для связанных индуктивностей таким образом, что M будет положительной величиной. Для этого следует считать положительными токи, которые втекают в соответствующие выводы индуктивностей (соответствующие с учётом фазировки; при разомкнутых зажимах одной из индуктивностей и изменении тока через другую, напряжения на соответствующих выводах изменяются синфазно). На рис. %img:l1l2 соответствующие выводы обозначены точками.

Здесь будем придерживаться второго подхода, т.е. выбирать положительные направления для токов в связанных индуктивностях так, чтобы взаимная индуктивность была положительной.

Основные свойства взаимной индуктивности

1. Свойство взаимности (независимость взаимной индуктивности от перестановки индексов). Для двух связанных индуктивностей, как уже было отмечено выше, справедливо равенство $ M_ = M_. $ Кстати, свойство взаимности остаётся справедливым и для случая нескольких связанных индуктивностей, (M_=M_), но здесь ограничимся рассмотрением только двух индуктивностей.

2. Максимально возможное значение взаимной индуктивности между двумя катушками не может превышать среднего геометрического их индуктивностей: $ M le sqrt, $ где L1, L2 — индуктивности катушек. Это означает, что как бы мы ни старались увеличить связь между двумя катушками, скажем, сближая их, взаимная индуктивность не может получиться больше указанной величины.

Свойство даёт нам возможность ввести другую удобную величину, характеризующую степень связи двух индуктивностей — коэффициент связи k, $ k = frac M >. $ Величина k безразмерная, может принимать значения от 0 до 1. Величине 0 соответствует полное отсутствие магнитной связи между индуктивностями. Коэффициент, равный 1, говорит о совершенной связи между двумя индуктивностями (магнитный поток одной катушки полностью пронизывает другую).

Нулевой коэффициент стремятся получить, если требуется максимально развязать между собой некоторые участки цепи, когда их взаимное влияние препятствует нормальной работе устройства. К единичному коэффициенту стремятся, когда задача состоит в наиболее эффективной передаче энергии от одной индуктивности к другой посредством магнитного поля (например, в трансформаторах).

3. Энергия, запасённая системой двух магнитно связанных индуктивностей равна $ W=frac 2 + frac 2 + M i_1 i_2. $ Данное соотношение с натяжкой можно отнести к свойствам собственно M, но всё же оно приведено здесь, потому как два предыдущих свойства очень просто обосновать в процессе вычисления W.

Заметим, что токи в формуле — алгебраические величины, в зависимости от выбранных положительных направлений в цепи, они могут быть как положительными, так и отрицательными. Поэтому энергия, запасённая двумя связанными индуктивностями, может быть как больше, так и меньше энергии двух независимых катушек с такими же индуктивностями при таких же токах через них.

ru_radio_electr

Поясните на пальцах, что такое и как себя ведет: отрицательная емкость, отрицательная индуктивность и отрицательный резистор. А то мне что-то сложно представить.

На первое наткнулся в электромеханической эквивалентной схеме пьезопреобразователя, другие назвал по индукции.

LJ Video

27 comments
—
Leave a comment

April 15th, 2009 , 07:44 am

речь идёт скорее не об устройствах как таковых, а о характеристиках сопротивления, т.н. импедансе.
есть например, усилители звука с отрицательным сопротивлением.
отрицательная ёмкость пьезика говорит видимо о том что его емкостное сопротивление в зависимости от частоты ведёт себя так же как у обычных кондёров, но с противоположным знаком.
отрицательную индуктивность представить сложно, может быть какие-нибудь электронные дроссели такое умеют, не знаю 🙂

April 15th, 2009 , 07:54 am

если и невозможно такое реализовать, то давайте хоть представим

рост импеданса с частотой — вот что значит отрицательная емкость? ну так это можно было реализовать менее экзотическими способами

April 15th, 2009 , 08:01 am

ну да, емкость и индуктивность же двойственные вещи, поэтому не удивлюсь если отрицательную ёмкость обзовут «виртуальной индуктивностью» и наоборот 🙂

April 15th, 2009 , 08:18 am

Лет давно назад потребовалась мне для эквалайзера отрицательная индуктивность. Сделал гиратор на ОУ. По учебнику И.Достал «Операционные усилители».

April 15th, 2009 , 04:11 pm
якобы гираторы бывают с отрицательной индуктивностью
April 15th, 2009 , 07:46 am

Отрицательный резистор — это тот, напряжение на котором равно по модулю току, протекающему через резистор, умноженному на сопротивление, а по знаку — противоположно ему.

То есть внутри этого резистора должен быть управляемый источник ЭДС.

April 15th, 2009 , 07:59 am

Не обязательно источник внутри. Есть множество реальных двухполюсников (напр., туннельный диод, лямбда-диод), имеющих на ВАХ участок с отрицательным сопротивлением.

April 15th, 2009 , 08:05 am
April 15th, 2009 , 10:32 am

Это участок диференциального отрицательного сопротивления, то есть отрицательное оно только как разница с ближайшим фрагментом ВАХ. А так глобально, считая в точке и по закону Ома — вполне себе позитивное.

Чтобы совсем правильное отрицательное сопротивление сделать — нужен операционник и источник питания к нему.

April 15th, 2009 , 07:59 am

придумалось вот что:
два последовательных резистора в цепи, с одного снимаем напряжение, подаем на усилитель, выход из усилителя подаем на другой резистор с обратной полярностью. так?
получается обратная связь, которая будет давить возмущения в цепи

April 15th, 2009 , 08:03 am

да с отрицательным сопротивлением всё довольно просто. реализуется в рамках некоторых ограничений при помощи операционников.

April 15th, 2009 , 08:33 am
не надо операционники, любая няонка обладает отрицательным сопротивлением 🙂
April 15th, 2009 , 03:24 pm
дифференциальным.
April 15th, 2009 , 07:15 pm

зачем неонка? это несовременно

и реализуем вообще всё что угодно (даже нереализуемое физически)

April 15th, 2009 , 07:55 am
а речь точно не о динамическом параметре?
April 15th, 2009 , 08:18 am
вроде бы не динамический
точнее не понял, так как не понял что это вообще такое
April 15th, 2009 , 07:07 pm

тьфу блин, о дифференциальном

бывает отрицательное дифференциальное сопротивление, почему бы не быть отрицательной дифференциальной ёмкости?

April 15th, 2009 , 07:56 am

У меня при измерении ВАХ сверхпроводников частенько вылазит отрицательное омическое (выходящее из нуля) сопротивление. Откуда берется я не знаю. Пытался найти причину откуда оно берется но в итоге так и не понял, просто вычитаю ее из вольтамперки. Но наблюдать эффект реально диковато — я подаю ток, а у меня по линейному закону возникает напряжение обратного знака.

April 15th, 2009 , 08:02 am

имхо:
Ток создает магнитное поле, поле где-то наводит эдс. Отследить сложно, как и вообще все наводки.

April 15th, 2009 , 11:43 am
ээээ
а в чём глубокий смысл измерения ВАХ у куска провода с нулевым сопротивлением?
April 15th, 2009 , 02:04 pm
Чтобы убедиться что сопротивление действительно нулевое.
April 15th, 2009 , 02:28 pm
Ну это в наше время уже просто баловство 🙂
April 15th, 2009 , 02:28 pm

Оно нулевое только при I меньше Iкрит. В сверхпроводниках 2-го рода, дальше возникает псевдосопротивление, связанное с течением флаксонов (магнитного потока) под действием силы Лоренца, так что ступенькообразного перехода R=0 -> R=Rn как в классических сверхпроводниках нету, ВАХ относительно плавные. Ну а так как ВТСП это керамики, характеристики которых в значительной мере зависят от качества микроструктры, то дальше возникают распределения критического тока вдоль сверхпроводника, различные дефекты, примеси. Так что, например, при измерении ВАХ можно обнаруживать слабые звенья, ограничивающи транспорт тока.

April 15th, 2009 , 03:00 pm
Спасибо, сообразил! А то я работаю с обычными сверхпроводящими соленоидами, у них всё просто.
April 16th, 2009 , 02:09 am

Ну я с ВТСП работаю всего три года и за это время только и смог понять, насколько там все сложно 🙂

А что касается токоограничвающих микродефектов, то мы можем с помощью лазерного микро-сканирования выявлять даже их позиции в сверхпроводящей пленке. Иногда бывает, что дефекты имеют настолько маленький критический ток и при этом микронный размер, что большая часть сверхпроводника находится в состоянии с нулевым сопротивлением, тогда как из-за локальных преград общее падение напряжение на проводе уже не нулевое. Одно из важных направлений технической науки ВТСП — это как раз изучение таких дефектов с целью улучшение процесса производства — для достижения как можно более равномерного транспорта тока по сечению сверхпроводящего провода. Сейчас уже есть современные сверхпроводящие ленты (уже инженерной длины), у которых критический ток в собственном магнитном поле приближается к критическому току монокристаллов. То есть благодаря вот этому медленному копошению постепенно стали выжимать из сверхпроводников почти максимум.

April 16th, 2009 , 07:10 pm

о, может вы знаете?
я краем уха где-то слышал, что уже делают серийно лабораторные магниты из ВТСП на несколько тесла. Вы случайно не знаете, сколько такое чудо может стоить и где продаваться?

(Anonymous)
April 15th, 2009 , 02:55 pm

В описаниях схем на операционных усилителях посмотреть гиратор. Там достаточно полно описывается. Если на пальцах — то для некоторых двухполюсников уравнение связывающее ток и напряжение имеют знак минус Например для сопротивления U=IR, для отрицательного сопротивления: U=-IR. При ключении такого элемента последовательно в электрическую цепь он может полностью или частично компенсировать активное сопротивление.

27 comments
—
Leave a comment

Обоснование свойств взаимной индуктивности

Для обоснования перечисленных выше свойств взаимной индуктивности, вычислим энергию, запасённую системой из двух связанных индуктивностей.

Но прежде, в качестве упражнения, поясняющего используемый для вычисления подход, найдём энергию одиночной индуктивности L1. Напряжение на индуктивности $ u_1 = L_1 frac . $ Тогда мощность, передаваемая из цепи в индуктивность $ p_1 = u_1 i_1 = L_1 i_1 frac , $ а энергия, передаваемая за промежуток времени между моментами t1, t2 $ Delta W_1 = intlimits_^ p_1 dt = L_1 intlimits_^ i_1 frac dt = L_1 intlimits_>^> i_1 di_1, $ $ begin Delta W_1 = L_1 intlimits_>^> i_1 di_1, label end $ здесь мы перешли к новым пределам интегрирования i11, i12, соответствующим току через индуктивность в моменты времени t1 и t2. Интегрируя, получаем $ Delta W_1 = frac ^2> 2 — frac ^2> 2. $

Получаемая индуктивностью за рассматриваемый промежуток времени энергия может быть как больше нуля (если i1(t2) > i1(t1)), так и меньше нуля (если i1(t2) < i1(t1)). Иначе говоря, индуктивность может получать энергию из цепи, к которой подключена, а может отдавать запасённую энергию в цепь. Идеальная индуктивность запасает получаемую энергию без потерь: как видно из формулы, если величина тока через индуктивность возвращается к начальному значению, полученная энергия оказывается равной 0, т.е. запасаемая во время роста тока энергия, полностью возвращается в цепь при снижении тока.

Из формулы получаем, что если в начальный момент ток через индуктивность равен 0 (и запасённая энергия равно 0), то энергия, запасённая в индуктивности в любой момент времени составит $ W_1=frac 2. $ Эта энергия зависит только от индуктивности катушки и величины тока в данный момент (в квазистационарном приближении). Величина не может быть отрицательной (индуктивность может отдавать запасённую энергию, но не является генератором — не может отдать больше, чем было запасено перед этим).

Теперь перейдём к вычислению энергии, запасаемой системой из двух связанных индуктивностей, которая описывается уравнениями (ref). Пока мы предполагаем, что коэффициенты взаимной индукции в уравнениях могут быть различными. $ begin begin u_1 = L_1 frac + M_ frac \ u_2 = M_ frac + L_2 frac . end end label $ Получаемая из цепи мощность равна сумме мощностей, получаемых каждой из индуктивностей: $ p = p_1 + p_2 = u_1 i_1 + u_2 i_2, \ p = L_1 i_1 frac + M_ i_1 frac + M_ i_2 frac + L_2 i_2 frac . $ Пусть в начальный момент токи через индуктивности равны 0, запасённая энергия отсутствует. Тогда запасаемая связанными индуктивностями энергия к некоторому моменту времени (tau) составит $ W(tau) = intlimits_^ p dt = \ = intlimits_^ left( L_1 i_1 frac + M_ i_1 frac + M_ i_2 frac + L_2 i_2 frac right) dt, $ $ begin W(tau) = L_1 intlimits_^ i_1 di_1 + M_ intlimits_^ i_1 di_2 + M_ intlimits_^ i_2 di_1 + L_2 intlimits_^ i_2 di_2. label end $ Для простоты записи, мы не переходим к новым пределам интегрирования (как в (ref)), поскольку выражение вида $ intlimits_^ i_x di_y $ будем считать просто краткой формой $ intlimits_^ i_x(t) d(i_y(t)) $ и при вычислениях в нужный момент всегда сможем перейти к требуемым величинам.

Первое и последнее слагаемое в (ref) вычисляются элементарно, получаемый для них результат совпадает со значением энергии для уединённой индуктивности, т.е. (L i^2/2). Тогда получаем $ W(tau) = frac 2 + frac 2 + M_ intlimits_^ i_1 di_2 + M_ intlimits_^ i_2 di_1. $ Если мы преобразуем один из интегралов в последнем выражении, используя метод интегрирования по частям, т.е. используя формулу $ int u dv = uv — int v du $ или для определённого интеграла $ intlimits_a^b u dv = left. uv right|_a^b — intlimits_a^b v du, $ то приведём оба интеграла к одному виду и тем самым упростим выражение. Преобразуем, например, первый интеграл $ intlimits_^ i_1 di_2 = left. i_1 i_2 right|_0^ — intlimits_^ i_2 di_1. $ Или, с учётом того, что в начальный момент токи считаем равными 0, получаем $ intlimits_^ i_1 di_2 = i_1(tau) i_2(tau) — intlimits_^ i_2 di_1. $ Подставляем в выражение для расчёта накопленной энергии: $ begin W(tau) = frac 2 + frac 2 + M_ i_1(tau) i_2(tau) + (M_ — M_) intlimits_^ i_2 di_1. label end $

Как и в рассмотренном ранее случае уединённой индуктивности, так и здесь, запасённая энергия — это энергия магнитного поля индуктивностей, которая зависит от токов через индуктивности в данный момент и не зависит от токов в предшествующие моменты (в квазистационарном приближении). Полученное выражение отвечало бы этому условию, если бы не последнее слагаемое, интеграл в котором зависит от того, каким образом (по какому закону) изменялись токи через индуктивности во всём рассматриваемом промежутке времени, от начального до текущего момента. Требование однозначности энергии при заданных токах будет выполнено только в том случае, если (M_ = M_), тогда последнее слагаемое в (ref) всегда равно 0.

Обозначая взаимную индуктивность просто как M, окончательно получаем формулу для вычисления запасённой энергии в любой момент времени $ begin W = frac 2 + frac 2 + M i_1 i_2, label end $ где i1, i2 — мгновенные значения тока через первую и вторую индуктивность в момент времени, для которого вычисляется W.

Итак, свойство взаимности подтверждено, энергия связанных индуктивностей вычислена. Но это ещё не всё, из (ref) можно сделать определённые выводы насчёт соотношения между индуктивностями и взаимной индуктивностью, если принять во внимание то, что всегда, (как и в случае одной индуктивности), запасённая энергия является неотрицательной величиной. То есть, при любых значениях i1, i2 и любых их знаках выполняется условие $ W ge 0 $ или $ begin frac 2 + frac 2 + M i_1 i_2 ge 0. label end $ Условие, повторим ещё раз, должно выполняться при любом сочетании токов через индуктивности. Если хотя бы один из токов равен нулю или токи имеют одинаковый знак, то, очевидно, условие выполняется, так как тогда каждое из слагаемых положительно (или равно 0). Поэтому рассмотрим случай, когда токи не равны нулю и имеют разные знаки, т.е. $ i_1 i_2 lt 0 Rightarrow \ Rightarrow — i_1 i_2 gt 0 Rightarrow \ Rightarrow — i_1 i_2 = |i_1 i_2|. $ Тогда условие (ref) может быть записано в виде $ M le frac 1 <|i_1 i_2|>left( frac + frac right) $ или $ M le frac frac <|i_1|> <|i_2|>+ frac frac <|i_2|><|i_1|>. $ Полученное условие ограничивает максимально возможное значение взаимной индуктивности. Никакие конструктивные ухищрения не позволят добиться увеличения взаимной индуктивности сверх величины, соответствующей наименьшему возможному значению выражения $ frac frac <|i_1|> <|i_2|>+ frac frac <|i_2|><|i_1|>. $ Обозначим |i1|, |i2| соответственно как x, y (x > 0, y > 0) и найдём наименьшее значение функции $ f=frac frac x y + frac frac y x. $ Можно рассматривать её как функцию двух переменных или привести к функции одной переменной. Пусть $ y = z x \ (x gt 0, y gt 0 Rightarrow z gt 0), $ тогда $ f = frac frac x + frac frac x, \ f = f(z) = frac frac 1 z + frac z. $ Нетрудно заметить, что $ f(z) rightarrow + infty text < при>\ z rightarrow 0+ text < или >z rightarrow + infty, $ тогда наименьшее значение функция f(z) будет принимать в точке минимума z0, которую найдём из условия $ f'(z_0) = 0, \ — frac frac 1 + frac = 0, \ z_0^2 = frac , $ а с учётом того, что z > 0, $ z_0 = sqrt <frac >. $ Вычисляем наименьшее значение функции $ f_ = f(z_0) = frac sqrt <frac > + frac sqrt <frac > = frac > 2 + frac > 2, \ f_ = sqrt. $ Как мы выяснили, $ M le f_, $ то есть $ M le sqrt. $

Итак, вычисляя энергию связанных индуктивностей и рассматривая требования, которым она должна удовлетворять, нам удалось убедиться в справедливости важнейших свойств взаимной индуктивности.

Отрицательную индуктивность

На пути луча электронов установлены две пары взаимно перпендикулярных электродов б и 7 соответственно в горизонтальном и вертикальном направлениях. Если между пластинами 6 приложить напряжение, то электроны, отталкиваясь от отрицательно заряженной плаа-

объемного заряда, сзязянного с иглой, в сторону отрицательно заряженной плоскости. Поэтому пробой и наступает при меньшем напряжении, чем при противоположной полярности электродов, когда объемный заряд частично нейтрализует и экранизирует иглу с отрицательной полярностью от плоскости, заряженной положительно.

1.4. Две пластины, напряжение между которыми 2000 В, удалены друг от друга на расстояние 3 см. Электрон начинает двигаться от отрицательно заряженной пластины с начальной скоростью, равной нулю. Определить: а) через какое время электрон достигнет скорости 10* м/с; б) какой путь он пролетит, прежде чем достигнет такой скорости; в) какой разности потенциалов соответствует эта скорость; г) на сколько увеличится кинетическая энергия электрона в конце пути?

1.49. Электрон с начальной скоростью и0 вылетает из точки О, расположенной посередине между пластинами плоскопараллельного конденсатора ( 1.17). Расстояние между пластинами равно 1 см, а приложенное напряжение 100 В. а) Найти значение и направление индукции магнитного поля, которое заставит электрон двигаться по указанной на рисунке циклоиде. Учесть, что электрон имеет нулевую скорость в точке поворота на отрицательно заряженной пластине; б) какова должна быть скорость va, чтобы электрон двигался по этому пути?

От отрицательно заряженной оси расстояние до точки М равно:

Знак плюс берется при А , т.е. для полупространства с положительно заряженной осью. В первом случае окружности расположены справа от оси оу, во втором случае — слева.

ные ионы, попадая на отрицательно заряженную поверхность, теряют свои заряды. Также может иметь место столкновение электрона и нейтрального атома в объеме газа между контактами, а не на поверхности; в этом случае электрон заряжает нейтральный атом газа, отдавая ему заряд, а затем положительный ион, сталкиваясь с отрицательно заряженной частичкой газа, образует снова нейтральную частицу.

Решение. В средней оЗластн пространства между пластинами плоского конденсатора электрическое поле можно считать однородным. Линии напряженности электрического поля начинаются на поверхности положительно наряженной пластины и кончаются на поверхности отрицательно заряженной пластины. Эти линии перпендикулярны пластинам. Поэтому расстояние между пластинами равно длине линии напряженности электрического поля. Следовательно, электрическое напряжение, имеющееся между пластинами, поделенное на расстояние межцу ними, равно напряженности электрического поля:

От отрицательно заряженной оси расстояние до точки М равно:

Знак плюс берется при k 1, т. е. для полупространства с положительно заряженной осью. В первом случае окружности расположены справа от о:и Оу, во втором случае — слева.

Поляризованность диэлектрика можно охарактеризовать еще несколько иначе, связав определение поляризованности с фактом смещения в диэлектрике положительно и отрицательно заряженных частиц под действием поля. Пусть изолирующее вещество помещено в однородное электрическое поле между двумя заряженными металлическими пластинами. При установлении поля частицы с положительными зарядами в диэлектрике смещаются по направлению к отрицательно заряженной пластине в среднем на расстоя-

При даннрм способе реализации функции вида Z5 (р), которая не имеет ни иулей, ни полюсов на оси /со и имеет равную нулю вещественную часть Re [Z5 (/o)0)] при частоте со0. мы получили на одном этапе ; реализации отрицательное значение индуктивнссти L0 = — 1. Эт<> обстоятельство не должно нас смущать, так как в конечном «(чете эту отрицательную индуктивность можно реализовать введением в реальную цепь трансформатора, приближающегося по свЬим свойствам к совершенному трансформатору, т. е. с коэффициентом связи, равным единице (k=l). Параметры трансформатора в соответствии со значениями величин L0, L7 и L8 ( 15-16, :д) будут равны L’ =L0 + L7 = — 1 +2 = 1; L» = Lg +

Если Lt — L2, то Ll — 7W>>0 и L2 — M > 0, так как коэффициент связи k = Af//’L1L2 ша, то на основании (8-12) LJ > М и L2

Может ли индуктивность быть отрицательной

Эффекты, связанные с катушкой отрицательной энергии (КОЭ)

Здесь я собрал эффекты, связанные с явлением — Катушка Отрицательной Энергии (КОЭ) — которые были опубликованы за несколько лет в интернете.

Скачать:

Как результат интерпретации по главному принципу относительности, может быть найдено, что явление противоположной самоиндукции вызвано изменением относительной величины потока между одинаковыми типами электрических зарядов. В качестве использования явления, было бы возможно произвести электроэнергию из пространства при уменьшении энтропии. Теперь я представлю основной элемент схемы, создающий это.

Ток проводимости это относительный поток между свободными электронами, несущими отрицательный заряд и ионами, несущими положительный заряд. Короче говоря, это относительный поток между различными видами зарядов. В этом случае, происходит нормальная самоиндукция.

Для получения катушки отрицательной энергии необходимо ослабить величину самоиндукции.

Чтобы сделать это, надо положительные ионы заменить на отрицательные ионы, или свободные электроны должны быть заменены на позитроны. Однако это невозможно, исходя из понимания материи.

В конструкции катушке отрицательной энергии центральный, внутренний цилиндр-проводник заряжен положительно, а внешний цилиндр — подложка катушки -отрицательно. При этом в качестве подложки можно использовать так же и сам проводник катушки. Электроны на поверхности проводника обращенной к внутреннему цилиндру будут выполнять функцию отрицательно заряженной подложки.

Как видно из рисунка движущиеся электроны в соленоиде будут «видеть» магнитное поле ими создаваемое значительно ослабленное. И как результат величина самоиндукции будет тоже ниже. Получается электростатический экран магнитного поля для движущихся электронов в проводнике — поле отрицательной энергии.

Катушка забирает энергию из пространства, где проявляется относительное магнитное поле, и как противодействие, при этом катушка индуктивности производит положительную энергию как электроэнергию. Свободные электроны, которые получили кинетическую энергию от пространства — как ускорение, возвращают кинетическую энергию пространству — как замедление. В нормальном проводнике, свободные электроны теряют кинетическую энергию, сталкиваясь с атомами. В этом случае, атомы, увеличивают энергию вибраций от столкновения со свободными электронами (повышают температуру). В электрическом проводе катушки отрицательной энергии, кинетическая энергия электронов входит и из пространства, так, чтобы электроны слабо влияли на атомы. По этой причине, свободные электроны работают на уменьшение тепловых колебаний атомов. То есть катушка отрицательной энергии, приведенная в действие, становится прохладной. То же самое явление происходит в отрицательном проводнике. Хотя свободные электроны в проводнике делают движения в случайном направлении при сталкивании с атомами, эти свободные электроны влияют на скорости друг друга так, что ток не проявляется макроскопически. При условии, что проводник заряжен отрицательно, каждый свободный электрон, имеющий тепловое движение может приносить противоположную самоиндукцию при ускорении или замедлении. Соответственно, проводник с отрицательным зарядом охлаждается, и поле отрицательной энергии появляется в пространстве.

Таким образом — проводник в соленоиде, который стал относительно отрицательно заряжен, может рассматриваться как работающий отрицательный проводник.

При повышении тока на обмотке магнитное поле повышается, а при снижении уменьшается. Катушкой называется винтовая катушка в виде спирали из изолированного провода, с индуктивностью, при малой емкости и сопротивлении которая имеет единицу измерения Гн (Генри) и определяется по формуле:

L = Φ / I, где L – индуктивность катушки, I – сила тока, Φ – магнитный поток.

Катушка обладает некоторой особенностью. При подаче на нее постоянного напряжения, в ней образуется напряжение, противоположное по знаку, и длящееся очень короткий промежуток времени. Это явление назвали ЭДС самоиндукции. ЭДС – это электродвижущая сила.

При размыкании цепи напряжение и ЭДС суммируются поэтому, сначала ток будет иметь двойную величину, а затем упадет до нуля. Время падения тока зависит от величины индуктивности катушки.

Виды катушек

Катушки можно разделить на типы:

С магнитным сердечником. Его материалом может быть сталь, ферритовый сердечник. Они предназначены для увеличения величины индуктивности.
Без сердечника. Катушки наматываются в виде спирали, на бумажной трубке. Применяются для создания незначительной индуктивности (до 5 мГн).

Чаще всего применяют сердечники из пластин, выполненных из электротехнической стали, для снижения вихревых токов, а также сердечники в виде ферритовых колец различных размеров (тороидальные), обеспечивающие создание значительной индуктивности, в отличие от обычных цилиндрических сердечников.

Катушки со значительной величиной индуктивности выполняют в виде трансформатора с металлическим сердечником. От обычного трансформатора они отличаются числом обмоток. В такой катушке есть одна первичная обмотка, а вторичной нет.

Особенности

При соединении нескольких катушек по параллельной схеме, необходимо следить, чтобы они были расположены на плате друг от друга как можно дальше, во избежание взаимного влияния катушек друг на друга магнитными полями.
Расстояние между витками на тороидальном сердечнике не влияет на свойства индуктивной катушки.
Для создания наибольшей индуктивности витки на катушке необходимо наматывать вплотную между собой.
При использовании в качестве сердечника ферритового цилиндра с наибольшей индуктивностью будет центр.
Чем меньше число витков на катушках, тем ниже у них индуктивности.
При последовательной схеме соединения катушек, общая индуктивность цепи складывается из индуктивностей каждой катушки.

Емкость катушки

Витки обмотки катушки отделены друг от друга диэлектрическим слоем, поэтому они образуют своеобразный конденсатор, который характеризуется своей емкостью. В катушках, имеющих несколько слоев обмотки, емкость образуется между слоями. В результате, катушка имеет свойство не только индуктивности, но и емкости.

Чаще всего емкость катушки оказывает отрицательное воздействие на элементы электрической схемы. Поэтому от емкости катушки избавляются разными способами. Например, каркас катушки изготавливают особой формы, витки наматывают по специальной технологии. При намотке катушки виток к витку, ее емкость также повышается.

Колебательный контур

Если подключить конденсатор и катушку по схеме, изображенной на рисунке, то получается контур колебаний, который широко применяется в радиотехнических устройствах.

Если навести ЭДС в катушке или зарядить конденсатор, то в контуре будут происходить некоторые колебательные процессы. Конденсатор при разряде возбуждает магнитное поле в катушке индуктивности. При истощении заряда конденсатора, катушка возвращает энергию снова в конденсатор, но с противоположным знаком, с помощью ЭДС самоиндукции. Такой процесс повторяется в виде электромагнитных синусоидальных колебаний.

Частота таких колебаний является резонансной частотой, зависящей от индуктивности катушки и емкости конденсатора. Колебательный контур, соединенный по параллельной схеме имеет значительное сопротивление на частоте резонанса. Это дает возможность применять его для избирательности частоты в цепях входа в радиоаппаратуре, а также в усилителях частоты и схемах генераторов частоты.

При параллельной схеме соединения контура колебаний имеются два реактивных элемента, которые обладают разной силой реактивности. Применение такого типа контура позволяет сделать вывод, что при параллельном соединении элементов необходимо суммировать только их проводимости, а не сопротивления. На частоте резонанса сумма проводимостей элементов контура нулевая, что позволяет говорить о сопротивлении переменному току стремящемуся к бесконечности.

За 1 период колебаний действия контура происходит обмен энергией между катушкой и емкостью. В таком случае образуется контурный ток, значительно превосходящий величину тока во внешней цепи.

Индуктивность и конденсатор

Токоведущие части различных устройств могут образовывать индуктивности. Такими частями являются предохранители, токоотводящие шины, соединительные выводы и другие аналогичные части. Если дополнительно присоединить к конденсатору шины, то образуется индуктивность, которая оказывает влияние на работу электрической цепи. Также, на работоспособность цепи влияет емкость и сопротивление.

Индуктивности, образующияся на частоте резонанса вычисляется по формуле:

Ce = C / (1 – 4Π2f2LC), где Ce – это емкость конденсатора (эффективная), f – частота тока, L – индуктивность катушки, С – действительная емкость, П – число «пи».

Величина индуктивности должна всегда учитываться в схемах с силовыми конденсаторами большой емкости. В схемах с импульсными конденсаторами важным фактором является значение собственной индуктивности. Разряд таких конденсаторов происходит на индуктивные контуры, делящиеся на виды:

Колебательные.
Апериодические.

В конденсаторе индуктивность зависит от вида соединения элементов в схеме. При параллельной схеме это значение складывается из индуктивностей элементов схемы. Для снижения индуктивности электрического устройства, необходимо токопроводящие части конденсатора расположить таким образом, чтобы магнитные потоки компенсировались, то есть, проводники с одним направлением тока располагают как можно дальше друг от друга, а с противоположным направлением – рядом друг с другом.

При сближении токоведущих частей и уменьшении диэлектрического слоя можно добиться снижения индуктивности секции конденсатора. Это достигается с помощью разделения одной секции на несколько небольших емкостей.