Логические выражения играют центральную роль в информатике и программировании. Они позволяют нам выражать и интерпретировать условные ситуации, принимать решения и строить сложные алгоритмы.
· Обновлено 7 сентября 2023
Основные логические операции
- Инверсия (отрицание) — это операция, которая преобразует значение истина в значение ложь и наоборот. Обозначается чаще всего символом ¬ или !. Если A — это некоторое логическое выражение, то инверсия этого выражения будет обозначаться как ¬A или !A. Пример:
- Если A = истина, то ¬A = ложь.
- Если A = ложь, то ¬A = истина.
- Конъюнкция (логическое «И») — это операция, которая возвращает значение истина только в том случае, если оба её операнда имеют значение истина. Обозначается символом ∧ или . Таблица истинности конъюнкции:
- A = истина, B = истина -> A ∧ B = истина.
- A = истина, B = ложь -> A ∧ B = ложь.
- A = ложь, B = истина -> A ∧ B = ложь.
- A = ложь, B = ложь -> A ∧ B = ложь.
- Дизъюнкция (логическое «ИЛИ») — это операция, которая возвращает значение истина, если хотя бы один из её операндов имеет значение истина. Обозначается символом ∨ или ||. Таблица истинности дизъюнкции:
- A = истина, B = истина -> A ∨ B = истина.
- A = истина, B = ложь -> A ∨ B = истина.
- A = ложь, B = истина -> A ∨ B = истина.
- A = ложь, B = ложь -> A ∨ B = ложь.

Открыть диалоговое окно с формой по клику
Булевы типы
Результатом логического выражения всегда является булево (логическое) значение. Булев тип данных ( boolean ) может принимать только два значения: true (истина) или false (ложь). Эти величины упорядочены следующим образом: false < true .
var x, y: boolean; begin x := true; y := false; writeln(‘x = ‘, x); writeln(‘y = ‘, y); writeln(‘x < y = ‘, x < y); end.
x = TRUE y = FALSE x < y = FALSE
Операции and , or , not (применяемые к булевским операндам) дают булевские значения.
Это значит, что данные булевого типа являются не только результатом операций отношения, но и могут выступать в роли операндов операции отношения. Также к ним можно применять функции ord , succ , pred , процедуры inc и dec .
Значение типа boolean занимает в памяти 1 байт.
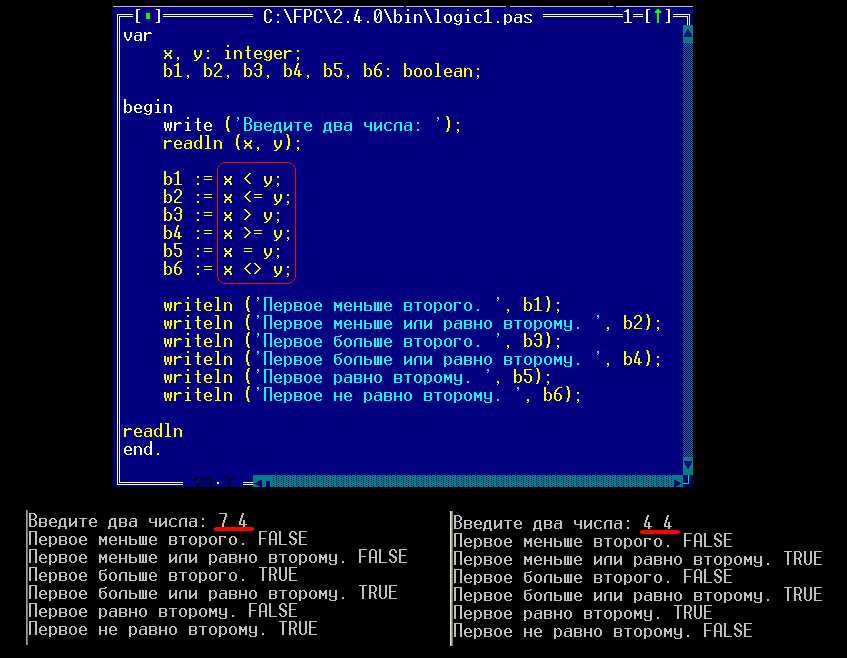
В примере шести булевым переменным присваиваются значения простых логических выражений. Значения, хранимые в таких переменных, затем выводятся на экран.
Кроме типа boolean в Pascal введены еще три булевых типа — bytebool (занимает 1 байт), wordbool (занимает 2 байта) и longbool (занимает 4 байта).
Логические выражения, таблицы истинности ,структурная логическая схема
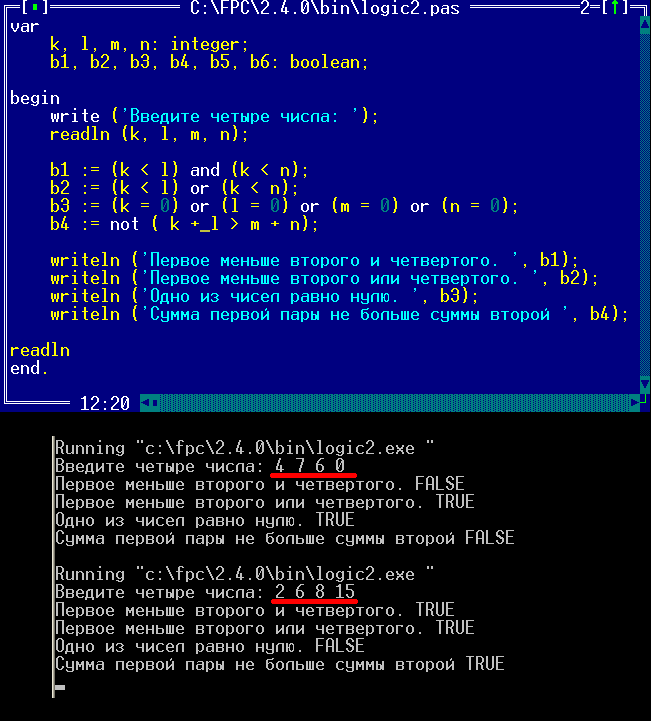
Для всех булевых типов значению false соответствует 0, а значению true — любое ненулевое значение. Логические переменные, принадлежащие разным булевым типам, ведут себя по-разному при выполнении над ними операций. Ниже приводится пример, реализованный на языке FreePascal (в комментариях отображается результат).
var b:boolean; wb:wordbool; begin b:= false; b:= pred(b); writeln(b,’ ‘,ord(b)); // TRUE 255 writeln(b=true); // TRUE wb:= false; wb:= pred(wb); writeln(wb,’ ‘,ord(wb)); // TRUE -1 b:= true; b:= succ(b); writeln(b,’ ‘,ord(b)); // TRUE 2 wb:= true; wb:= succ(wb); writeln(wb,’ ‘,ord(wb)); // FALSE 0 end.
Логические операции
С помощью логических операторов можно формировать сложные логические выражения. Логические операторы часто применяются по отношению к простым логическим выражениям.
В языке программирования Pascal предусмотрены следующие логические операции:
- Конъюнкция (логическое умножение, пересечение) — and . Выражение a and b дает значение true только в том случае, если a и b имеют значение true . Во всех остальных случаях значения выражения a and b дает false .
true and true = true true and false = false false and true = false false and false = false
true or true = true true or false = true false or true = true false or false = false
not true = false not false = true
true xor true = false true xor false = true false xor true = true false xor false = false
Последовательность выполнения логических операторов: not, and, or.
В языке Паскаль сначала выполняются логические операторы ( and , or , xor , not ), а уже потом операторы отношений ( > , >= , < , , = ), поэтому не нужно забывать расставлять скобки в сложных логических выражениях.
Сложные булевы выражения могут не обрабатываться до конца, если продолжение вычислений не изменит результат. Если булево выражение в обязательном порядке нужно обрабатывать до конца, то это обеспечивается включением директивы компиляции .
Логические выражения принимают только одно из двух значений истина или ложь
Тема: Логические основы компьютера.
1. Основы логики.
Логика – наука о законах и формах мышления.
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно.
Утверждение – суждение, которое требуется доказать или опровергнуть.
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
2. Логические элементы компьютера. Схемы логических элементов и их таблицы истинности.
Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т.п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.
Электронным элементом называется соединение различных деталей, в первую очередь – диодов и транзисторов, а также резисторов и конденсаторов, в виде электрической схемы, выполняющей некоторую простейшую функцию.
Электронный элемент, реализующий логическую функцию, называется логическим элементом.
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т.е. операции с предсказуемыми результатами, и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать задачи, используя язык двоичных кодов.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер, регистр, сумматор.
Триггер – это логическая схема, способная сохранять одно из двух состояний до подачи нового сигнала на вход. Это, по сути, разряд памяти, способный хранить 1 бит информации.
Регистр – это устройство, состоящее из последовательности триггеров. Регистр предназначен для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.
Сумматор – это устройство, предназначенное для суммирования двоичных кодов.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значение «ложь («0»).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
Таблица истинности – это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значениями истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логические операции и таблицы истинности
Табл. 9. Логическое умножение
Стандартные функции, возвращающие булевые значения
- odd(x) = true, если x нечетный ( x целый);
- eoln(x) = true, если встретился конец строки текстового файла x ;
- eof(x) = true, если встретился конец файла x .
В остальных случаях эти функции принимают значение false .
Логические операции. Результат сравнения может принимать только два значения: истина, когда высказы- вание справедливо
Результат сравнения может принимать только два значения: «истина», когда высказы- вание справедливо, или «ложь» — в противном случае. Говорят также, что истинность таких выражений либо «true» (t)(-1), либо «false» (f)(0).
Конструкция логических выражений в QBASIC довольно проста. В качестве сравниваемых значений (сравниваемых операндов) могут участвовать строки, числа, константы, переменные, арифметические и строковые выражения. Используют следующие операции сравнения:
| Операция | Значение |
| > | больше |
| меньше | |
| >= | больше или равно |
| меньше или равно | |
| = | равно |
| <> | Не равно |
Схематически условие можно представить следующим образом:
Выражение_1 Операция_сравнения Выражение_2
Для того чтобы сравнить строки (т.е. применить операторы «>» или » Итак, Строка_1 больше (меньше) Строки_2, если при посимвольном сравнении строк код первого несовпадающего символа из Строки_1 больше (меньше) кода соответствующего символа из Строки_2.
Числовые переменные(константы) сравниваются обычным образом.
Также в QВasic можно использовать переменные типа Boolean, т.е. переменные которым можно присвоить какое-то логическое выражение, и значение этой переменной будет зависеть от истинности или ложности определяющего выражения. Если значение выражения ложно, то переменной будет присвоено значение 0, а если истинно, то -1.
Пример:
‘Использование логических выражений
А=2>5
B=6 C=8<>9
PRINT A
PRINT B
PRINT C
END
‘Конец программы
В результате на экране вы увидите:
0
-1
-1
Также в логических выражениях можно использовать логические операции AND(и), OR(или), NOT(не), XOR(исключающее или, либо). Приведём таблицу истинности и приоритет операций.
| Выражение А | Выражение В | A AND B | A OR B | NOT A | A XOR B |
В программах часто возникает необходимость описывать более сложные логические выражения.
Рассмотрим пример:
‘Пример, подводящий читателя к применению более сложных логических условий
DIM zahl1%, zahl2%
CLS
INPUT «Ввести число 1, zahl1%
INPUT «Ввести число 2», zahl2%
‘Конец программы
Предположим входные данные должны вводится только тогда, когда zahll % больше нуля, и одновременно zahl1% меньше нуля. Как проверить одно из условий, Вы уже знаете. Рассмотрим способ, позволяющий объединить оба условия.
Логическое И (AND)
AND (И) коньюктивно объединяет логические условия:
Условие_1 AND Условие_2 [AND Условие_3] …
Результат такого объединения лишь тогда истинен, когда истинно каждое отдельное условие.
Пример:
DIM zahl1%, zahl2%
CLS
DO
INPUT «Введите число 1> 0», zahl1%
INPUT «Введите число 2 < 0 «, zahl2%
LOOP UNTIL zahll %>0 AND zahl2% < 0
PRINT «Спасибо за корректный ввод»
‘Конец программы
Логическое ИЛИ (OR)
OR (ИЛИ) дизъюнктивно объединяет логические условия:
Условие_1 OR Условие_2 [OR Условие_3. ]
Результат такого объединения только тогда ложен, когда ложны все составляющие.
Пример:
DIM zahl1%, zahl2%
CLS
DO
PRINT «Число 1 или число 2 должно быть больше нуля»
INPUT «Введите число 1», zahl1%
INPUT «Введите число 2», zahl2%
LOOP UNTIL zahl1% >0 OR zahl2% >0
PRINT «Спасибо за корректный ввод»
‘Конец программы
В этом примере выход из LOOP-цикла не произойдет только в том случае, если значение каждого из вводимых чисел будет меньше или равно нулю.
Логическое отрицание (NOT)
NOT инвертирует (меняет на противоположное) значение логического выражения, т.е. то, что было «ложь», становится «истиной» и наоборот.
Пример:
DIM zahl%
CLS
INPUT «Введите число » zahl%
IF NOTzahl% > 0 THEN
PRINT «Число не больше нуля»
ELSE
PRINT «Число больше нуля»
END IF
‘Конец программы
ЭТАПЫ РАЗВИТИЯ ЛОГИКИ
Огастес де Морган (1806 – 1871, шотландский
математик и логик) изложил (1847) элементы логики
высказываний и логики классов,
дал первую развитую систему
алгебры отношений.
Платон Сергеевич Порецкий (1846-1907) – русский
астроном, математик.
Автор первых в России трудов по
математической логике, активно занимался
популяризацией этой дисциплины, первый из
русских учёных, кто читал лекции
по математической логике.
Занимался проблематикой алгебры
высказываний. Его работы оказали влияние на
последующие исследования в данной области.
Хотя основной его специальностью была астрономия, как астроном
Порецкий малоизвестен, популярность ему принесло его
«хобби» — занятия математической логикой.
ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Логика оказала влияние на развитие математики, прежде
всего теории множеств, функциональных систем,
алгоритмов, рекурсивных функций.
В гуманитарных науках (логика, криминалистика).
Математическая логика является средством для изучения
деятельности мозга – для решения этой самой важной
проблемы биологии и науки вообще.
Идеи и аппарат логики используется в кибернетике,
вычислительной технике и электротехнике (компьютеры
построены на основе законов математической логики).
Идеи и аппарат логики используется в программировании,
базах данных и экспертных системах (PROLOG – язык
логического программирования).
1938 г. – американский инженер и
математик и инженер Клод
Шеннон (1916 – 2001) связал
Булеву алгебру (аппарат
математической логики),
двоичную систему кодирования и
релейно-контактные
переключательные схемы,
заложив основы будущих ЭВМ.
Логические выражения принимают только одно из двух значений истина или ложь
Тема: Логические основы компьютера.
1. Основы логики.
Логика – наука о законах и формах мышления.
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно.
Утверждение – суждение, которое требуется доказать или опровергнуть.
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом.
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение.
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0).
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
2. Логические элементы компьютера. Схемы логических элементов и их таблицы истинности.
Как при строительстве дома применяют различного рода типовые блоки – кирпичи, рамы, двери и т.п., так и при разработке компьютера используют типовые электронные схемы. Каждая схема состоит из определенного набора типовых электронных элементов.
Электронным элементом называется соединение различных деталей, в первую очередь – диодов и транзисторов, а также резисторов и конденсаторов, в виде электрической схемы, выполняющей некоторую простейшую функцию.
Электронный элемент, реализующий логическую функцию, называется логическим элементом.
Логический элемент компьютера – это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Тысячи микроскопических электронных переключателей в кристалле интегральной схемы сгруппированы в системы, выполняющие логические операции, т.е. операции с предсказуемыми результатами, и арифметические операции над двоичными числами. Соединенные в различные комбинации, логические элементы дают возможность компьютеру решать задачи, используя язык двоичных кодов.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер, регистр, сумматор.
Триггер – это логическая схема, способная сохранять одно из двух состояний до подачи нового сигнала на вход. Это, по сути, разряд памяти, способный хранить 1 бит информации.
Регистр – это устройство, состоящее из последовательности триггеров. Регистр предназначен для хранения многоразрядного двоичного числового кода, которым можно представлять и адрес, и команду, и данные.
Сумматор – это устройство, предназначенное для суммирования двоичных кодов.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Чтобы представить два логических состояния «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.
Высокий уровень обычно соответствует значению «истина» («1»), а низкий – значение «ложь («0»).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Работу логических элементов описывают с помощью таблиц истинности.
Таблица истинности – это табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значениями истинности выходного сигнала (результата операции) для каждого из этих сочетаний.
Логические операции и таблицы истинности
Табл. 9. Логическое умножение




