Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2 n , где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
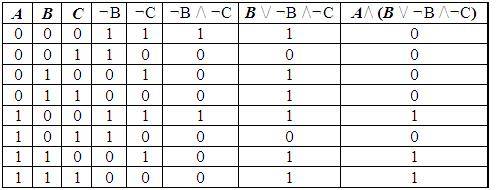
Пример 1. Для формулы A/ (B / ¬B /¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А/ В)/(¬А/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2 n , m=2 2 =4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А/ В; 2) ¬А; 3) ¬В; 4) ¬А/¬В; 5) (А/ В)/(¬А/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А
В
А/ В
¬А
¬В
¬А/¬В
F
0
1
1
0
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A/ B) / ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 2 3=8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А/ В; 2) ¬С; 3) (AVB) / ¬С .
- количество столбцов таблицы = 3 + 3 = 6
А
Высказывания. Логические значения высказываний. Логические операции [8 класс]
В
С
A/B
(A/B) / ¬С
0
0
1
0
1
0
1
0
Пример 4. Определите истинность формулы: F = ((С /В) => В) / (А / В) => В.
Построим таблицу истинности этой формулы.
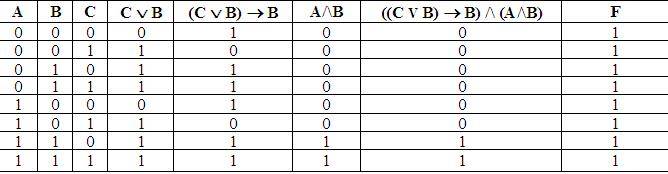
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
X
Y
Z
F
¬X/¬Y/Z
¬X/¬Y/Z
X/Y/¬Z
X/Y/Z
1
1
0
0
1
1
Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X/Y/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
3. Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов- падают, называются равносильными. Для обозначения равносильных логических выражений используется знак « = ». Докажем, что логические выражения  равносильны. Построим сначала таблицу истинности логического выражения
равносильны. Построим сначала таблицу истинности логического выражения  (табли- ца 9). Таблица 9 – Таблица истинности логического выражения
(табли- ца 9). Таблица 9 – Таблица истинности логического выражения 
| А | В | |||
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |

Теперь построим таблицу истинности логического выражения (таблица 10). Таблица 10 – Таблица истинности логического выражения
| А | В | А v В | |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:  =
=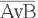 .
.
Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы. Для формулы, которая содержит две переменные, таких наборов значений
| переменных всего четыре: | |||
| (0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
| переменных восемь: | |||||||
| (0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул. Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере- менные X и Y . В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11: Таблица 11 – Таблица истинности для формулы с переменными Х и У Пример 2 Cоставить таблицу истинности сложного логического выражения: D = неA B.
Таблица истинности для конъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
| A | неА |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Основные логические операции
- Инверсия (отрицание) — это операция, которая преобразует значение истина в значение ложь и наоборот. Обозначается чаще всего символом ¬ или !. Если A — это некоторое логическое выражение, то инверсия этого выражения будет обозначаться как ¬A или !A. Пример:
- Если A = истина, то ¬A = ложь.
- Если A = ложь, то ¬A = истина.
- Конъюнкция (логическое «И») — это операция, которая возвращает значение истина только в том случае, если оба её операнда имеют значение истина. Обозначается символом ∧ или . Таблица истинности конъюнкции:
- A = истина, B = истина -> A ∧ B = истина.
- A = истина, B = ложь -> A ∧ B = ложь.
- A = ложь, B = истина -> A ∧ B = ложь.
- A = ложь, B = ложь -> A ∧ B = ложь.
- Дизъюнкция (логическое «ИЛИ») — это операция, которая возвращает значение истина, если хотя бы один из её операндов имеет значение истина. Обозначается символом ∨ или ||. Таблица истинности дизъюнкции:
- A = истина, B = истина -> A ∨ B = истина.
- A = истина, B = ложь -> A ∨ B = истина.
- A = ложь, B = истина -> A ∨ B = истина.
- A = ложь, B = ложь -> A ∨ B = ложь.

Открыть диалоговое окно с формой по клику
Влияние на работу компьютера
Логические операции составляют основу работы вычислительных систем. На физическом уровне компьютеры основаны на транзисторах, которые могут находиться в одном из двух состояний: открытое (проводящее) или закрытое (непроводящее). Эти состояния соответствуют логическим значениям истина и ложь.
Комбинации транзисторов могут выполнять базовые логические операции, такие как инверсия, конъюнкция и дизъюнкция. Таким образом, при помощи логических операций компьютеры могут выполнять сложные алгоритмы, принимать решения и обрабатывать информацию.
В программировании логические выражения используются для создания условных конструкций, циклов и других элементов управления потоком выполнения программы.
Понимание логических операций и их свойств критически важно для изучения информатики. Они являются основой для разработки алгоритмов, программирования и, в конечном итоге, для всего, что делает компьютер таким мощным инструментом.
Штрих Шеффера
Булева функция двух переменных или бинарная логическая операция. Введена в рассмотрение Генри Шеффером в 1913 г.
Обозначения: $|$, эквивалентно операции И-НЕ.
Таблицей истинности для функции штрих Шеффера
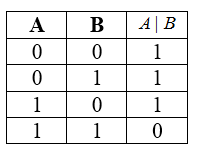
Штрих Шеффера образует базис для всех булевых функций двух переменных. Применяя штрих Шеффера можно построить остальные операции, например,
$X mid X = ¬X$ — отрицание
$(X mid Y) mid (X mid Y) = (X wedge Y)$ — конъюнкция
$(X mid X) mid (Y mid Y) = X vee Y$ — дизъюнкция
Для электроники это означает, что реализация схем возможна с использованием одного типового элемента (правда это дорогостоящий элемент).
Порядок выполнения логических операций в сложном логическом выражении
- Инверсия(отрицание);
- Конъюнкция (логическое умножение);
- Дизъюнкция и строгая дизъюнкция (логическое сложение);
- Импликация (следствие);
- Эквивалентность (тождество).
Для того чтобы изменить указанный порядок выполнения логических операций, необходимо использовать скобки.




