Статья рассматривает логические операции и их применение в программировании, а также дает примеры использования и объясняет основные свойства этих операций.
Логические операции: ключевые инструменты для решения задач в программировании обновлено: 29 сентября, 2023 автором: Научные Статьи.Ру
Помощь в написании работы
В данной лекции мы будем изучать логические операции и их применение в программировании. Логические операции позволяют нам работать с логическими значениями (истина или ложь) и принимать решения на основе этих значений. Мы рассмотрим основные логические операторы, их применение в условных выражениях и примеры использования в программировании. Также мы изучим свойства логических операций, которые помогут нам лучше понять их работу. Давайте начнем изучение этой важной темы!
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Повторяем определение логических операций
В алгебре логики изучаются логические операции, производимые над высказываниями. Такие высказывания могут быть истинными или ложными. Применяя к простым высказываниям логические операции, можно строить составные высказывания.
Повторим основные логические операции (буквами A, B или C будем обозначать элементарные логические высказывания):
Отрицание (инверсия, логическое НЕ) — это логическая операция, которая делает ложное высказывание истинным, а истинное — ложным.
Обозначение: ¬A, или not(A), или НЕ(A), или
Таблица истинности:
| A | |
| 0 | 1 |
| 1 | 0 |
Логическое сложение (дизъюнкция, логическое ИЛИ) — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно, и ложно тогда и только тогда, когда оба простых логических выражения ложны.
Обозначение: A ∨ B, или A or B, или A ИЛИ B, или A + B
Таблица истинности:
| A | B | A+B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логическое умножение (конъюнкция, логическое И) — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложное выражение ложно.
Обозначение: A ∧ B, или A and B, или A И B, или A * B
Преподаватели компьютерных курсов проходят бесплатное обучение во время отбора. У нас преподают Roblox, Unity, Unreal, Scratch, Construct 3, App Inventor, Minecraft, Thunkable, Web, Python.
Логические операции | Информатика 9 класс #2 | Инфоурок
Подробно рассказываем, как проходит обучение!

Таблица истинности:
| A | B | A * B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическое следование (импликация) — это сложное логическое выражение, которое истинно во всех случаях, кроме того случая, когда из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое (А) является условием, а второе (В) является следствием.
Обозначение: A → B
Таблица истинности:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая эквивалентность (равносильность) — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Обозначение: A ≡ B
Таблица истинности:
| A | B | A ≡ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическая операция XOR (сложение по модулю 2 или исключающее ИЛИ) — это логическая операция, по своему применению максимально приближенная к грамматической конструкции «либо … либо …».
Обозначение: A ⊕ B
Таблица истинности:
| A | B | A ⊕ B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
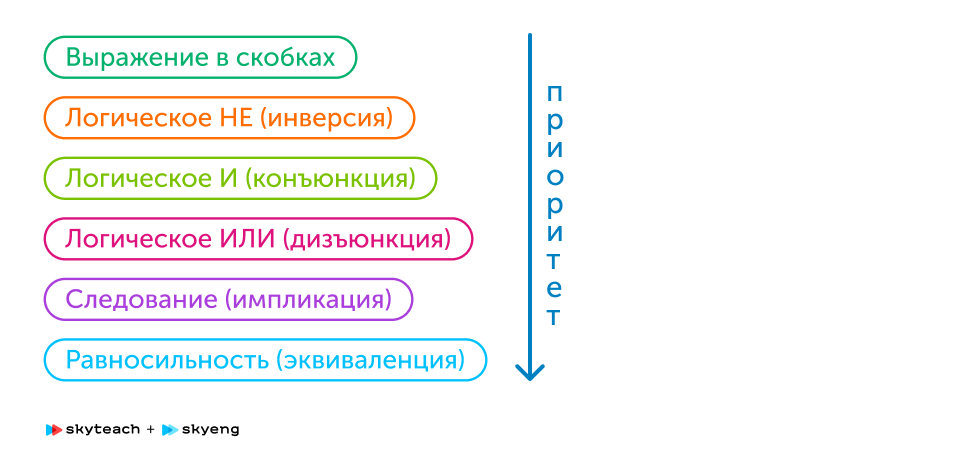
Вспоминаем порядок выполнения логических операций
Порядок выполнения логических операций в сложном логическом выражении:
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность
Для изменения указанного порядка выполнения логических операций используются скобки.
Законы алгебры логики — это некоторые стандартные преобразования логических выражений, при которых сохраняется равносильность.
1. Законы поглощения констант
2. Законы поглощения переменных
3. Законы идемпотентности
4. Закон двойного отрицания
= А
5. Закон противоречия
A * = 0
6. Закон исключенного третьего
A + = 1
7. Законы коммутативности
8. Законы ассоциативности
(A * B) * C = A * (B * C)
(A + B) + C = A + (B + C)
9. Законы дистрибутивности
A * (B + C) = (A * B) + (A * C)
A + (B * C) = (A + B) * (A + C) — обратите особое внимание!
10. Законы де Моргана
Правило для запоминания: «Крыша упала, знак поменяла (+ на *, * на +)».
11. Законы поглощения
12. Закон преобразования импликации
A → B = + B — импликация из A в B равна «не A плюс B»
Как пройти отбор в команду?
Вас ждет тест, знакомство с платформой, тренировочный урок, заполнение профиля.
Подробнее в статье «4 этапа отбора в Skysmart: как начать преподавать онлайн»

Влияние на работу компьютера
Логические операции составляют основу работы вычислительных систем. На физическом уровне компьютеры основаны на транзисторах, которые могут находиться в одном из двух состояний: открытое (проводящее) или закрытое (непроводящее). Эти состояния соответствуют логическим значениям истина и ложь.
Комбинации транзисторов могут выполнять базовые логические операции, такие как инверсия, конъюнкция и дизъюнкция. Таким образом, при помощи логических операций компьютеры могут выполнять сложные алгоритмы, принимать решения и обрабатывать информацию.
В программировании логические выражения используются для создания условных конструкций, циклов и других элементов управления потоком выполнения программы.
Понимание логических операций и их свойств критически важно для изучения информатики. Они являются основой для разработки алгоритмов, программирования и, в конечном итоге, для всего, что делает компьютер таким мощным инструментом.
Основные операции
Математика, информатика, программирование и другие науки немыслимы без анализа, а также построения теорий по заданным вопросам. Здесь без мышления логического характера не обойтись. Соответствующий момент активно применяется в приложениях — не только сложных, но и элементарных.
Чтобы понять, как работает логи ческая цепочка в калькуляторах истинности, стоит запомнить ключевые операции над логическими выражениями. Всего их несколько:
- конверсия;
- дизъюнкция;
- конъюнкция;
- строгая дизъюнкция;
- импликация;
- эквивалентность.
В программировании также стоит обратить внимание на запись исключающего или. Это – операция XOR.
Порядок обработки
При изучении формулы логики заданных высказываний стоит запомнить порядок (приоритет) обработки операций в сложном выражении. Выполняются манипуляции так:
- инверсия (логическое отрицание);
- конъюнкция (логическое умножение);
- дизъюнкция (логическое сложение);
- импликация;
- эквивалентность.
Для того, чтобы изменить прописанный порядок выполнения обработки данных, необходимо в логических выражениях использовать скобки.
Законы алгебры логики
Операции логики подчиняются законам, которые во многом напоминают математические законы. Другими словами, операции обладают определенными свойствами, которые упрощают решение и позволяют преобразовывать одни операции в другие.
Таблица законов алгебры логики

Диаграммы Эйлера-Венна
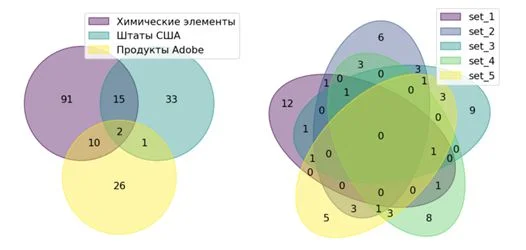
Тем, кто лучше воспринимает информацию в виде изображений, понравятся диаграммы Эйлера-Венна, которые показывают, как пересекаются множества между собой.
Число пересечений (областей) можно посчитать сразу, оно равно n = 2 N , где N – число множеств. Так как значение двойки в степени растет очень быстро (4,8,16), обычно диаграммы используют для 2-3 множеств. Далее области пересечения будут сливаться, образуя неразличимые участки. Если множеств 2-3, то рисуют круги, если больше 4 – эллипсы. Этот «цветок» помещают в прямоугольную конструкцию, которую называют универсум U (универсальное множество).
Источник

Источник
Диаграммы позволяют наглядно увидеть результат большинства логических функций:
Конъюнкция множеств А и В:


Сложное выражение (Ā)∨(A∧B), составленное из элементарных Ā, A∧B и их комбинации, графическое выражение:

Примеры использования диаграмм Эйлера-Венна
Есть 2 множества цифр и универсум:
Пустой области ничего не принадлежит, опишем в табличном виде, какие цифры какой области принадлежит:

Логическое сложение
В информатике часто используется такой вид операции, как дизъюнкция. Случай, когда нужно исключать истинное сложение — все подвыражения ложны. Символы, которые используются для обозначения операции: +, ∨. Базис свойств сложного сложения:
- любое подвыражение истинно, значит, вся дизъюнкция будет истинной;
- если все определения из списка ложны, тогда вся дизъюнкция ложна.
Результат не зависит от порядка расположения знаков логической операции. Для решения дизъюнкции используются 2 выражения. Первое: = «Лейбниц применил в информатике математические символы», второе: = «Лейбниц основал бинарную арифметику».

В результате преобразования описанных выражений получается следующий результат: «Идея использования в информатике математических символов принадлежит Лейбницу, или он основал бинарную арифметику».
Сложное высказывание считается ложным, если одновременно неверны два первоначальных понятия. В основе записи дизъюнкции находятся нули и единицы.
Использование частиц
Инверсия — ещё одна операция, которую применяют ежедневно операторы ЭВМ для обработки и передачи данных. Принцип преобразования отрицания: каждому тезису ставится новое высказывание, противоположное первоначальному. Инверсия либо отрицание означает, что к исходному выражению приставляется частица «не» либо слово «неверно», «что». Расшифровка логической операции:
- если первоначальное выражение является истиной, тогда его отрицание будет ложным;
- если исходное высказывание ложное, тогда его отрицание будет истинным.

Чтобы править запись инверсии, применяются специальные знаки логической операции: «НЕ», «А», «¬А». Для логического отрицания характерны некоторые свойства. Считается, что «двойное отрицание» (обозначается «¬ ¬A») — следствие суждения А. Оно указывает на тавтологию логического формата и равняется значению в булевой логистике.
Высказывание «Я имею компьютер» имеет отрицание «Неверно, что я имею компьютер» либо «У меня нет компьютера». Выражение «Я не знаю японский язык» имеет отрицание «Неверно, что я не знаю японский язык» либо «Я знаю японский язык». Другой пример инверсии: «Все ученицы 8 класса — отличницы». Отрицание можно составить следующим образом:
- «неверно, что все ученицы 8 класса — отличницы»;
- «не все ученицы 8 класса — отличницы».
Когда строится отрицание к простому высказыванию, либо применяется оборот из русского языка «неверно, что…», либо отрицание формируется для сказуемого, тогда к глаголу рекомендуется добавить частицу «не». Логическое умножение с символом «и» должно выполняться раньше сложения с «или».
Сложную операцию можно записать в виде выражения, в состав которого входят переменные, знаки и скобки. При этом необходимо соблюдать некоторую последовательность действий:
- инверсия;
- конъюнкция;
- дизъюнкция.

Для изменения порядка выполнения действия расставляются скобки. В конце выполненных операций проводится импликация. Это сложное выражение считается истинным в любом случае, исключение — из истины следует ложь. Операция позволяет связать 2 простых высказывания, из которых первое считается условием, а второе — следствием.
Для вычисления результата составного высказывания достаточно выяснить только значение 1 составного элемента. Если в схеме с «и» используется ложное простое высказывание, то результат составного будет ложным. Когда в составном предложении с «или» значения одного простого символа истинное, тогда результат всего выражения будет истинным.
Логическая операция исключающее ИЛИ (XOR).
Обозначение XOR: ^
Логическая операция исключающее ИЛИ выполняется с двумя битами (a и b). Результат выполнения логической операции XOR будет равен 1 (единице), если один из битов a или b равен 1 (единице), во всех остальных случаях, результат равен 0 (нулю). Смотрим таблицу истинности логической операции исключающее ИЛИ.
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Логическая операция НЕ (not)
Обозначение NOT: ~
Логическая операция НЕ выполняется с одним битом. Результат выполнения этой логической операции напрямую зависит от состояния бита. Если бит находился в нулевом состоянии, то результат выполнения NOT будет равен единице и наоборот. Смотрим таблицу истинности логической операции НЕ.
| 0 | 1 |
| 1 | 0 |
Запомните эти 4 логические операции. Используя эти логические операции, мы можем получить любой возможный результат. Подробно об использовании логических операций в С++ читаем тут.




