Колебательный контур это в физике

Содержание

Колебательный контур ― это электрическая цепь, содержащая катушку индуктивности и конденсатор. В такой электрической цепи происходят колебания электрического тока и напряжения, и взаимная трансформация энергии электрического поля и энергии магнитного поля.

Процессы в колебательном контуре
У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.

Если в цепи, кроме проводов и резисторов, находится катушка индуктивности, в равномерный и быстрый процесс перераспределения заряда вмешивается ЭДС самоиндукции катушки. Согласно правилу Ленца, втекающий в катушку ток вызывает ЭДС самоиндукции ― а ЭДС самоиндукции создает индуцированный ток, направленный так, чтобы препятствовать изменению тока в цепи. Если ток в цепи вдруг резко увеличивается ― индукционный ток стремиться его уменьшить, если ток в сети вдруг уменьшается ― индукционный ток стремиться его увеличивать.

Поэтому из―за катушки индуктивности заряд не переходит сразу через всю цепь, от одной обкладки конденсатора к другой. Сила тока в цепи медленно увеличивается ― потому что ее быстрому росту препятствует ЭДС самоиндукции катушки. Максимальной сила тока становится в тот момент, когда конденсатор разряжен (обе его обкладки обладают нулевым зарядом). В этот момент сила тока максимальна благодаря тому, что как только ее перестает наращивать конденсатор за счет потерянных зарядов ― ЭДС самоиндукции прекращает ей препятствовать.

Но разряженный конденсатор больше не может поддерживать силу тока ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.

После того как конденсатор зарядится ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.

Колебательный контур | ЕГЭ Физика | Николай Ньютон

Цикл процессов, происходящих в колебательном контуре:

1: Начальное состояние ― конденсатор заряжен до максимального заряда Qm, но силы тока в цепи пока нет.

2. Конденсатор разряжается ― заряд переходит от одной обкладки на другую через всю цепь, сила тока в цепи постепенно увеличивается.

3. Конденсатор разряжен ― весь заряд с обкладок уже ушел, сила тока в цепи максимальна и равна Im.

4. Конденсатор заряжается ― сила тока в цепи уменьшается, а конденсатор получает заряд.

5. Конденсатор перезаряжен ― но теперь та обкладка, которая была положительно заряженной, стала отрицательно заряженной, и наоборот. Тока в цепи нет.

6. Конденсатор вновь разряжается, но в обратную сторону ― и ток течет в сторону, обратную тому, что был на этапе 2.

7. Конденсатор разряжен ― ток достиг максимума, а заряда на конденсаторе нет.

Для постоянного тока сила тока определялась как количество заряда, прошедшее через сечение проводника за некоторый промежуток времени: I =∆q/ ∆t, где

Но переменный ток изменяет в цепи свою величину и свое направление, поэтому силу переменного тока определяют как производную количества заряда по времени:

Заряд в колебательном контуре изменяется по гармоническому закону q(t) = Qmaxsin(ωt + φ0), где

Qmax ― максимальный заряд (амплитуда колебаний заряда), [Кл];

ω ― циклическая частота колебаний [рад/с];

φ0 ― начальная фаза колебаний, [рад];

Следовательно, сила тока в контуре изменяется по закону I = qt’ = (Qmaxsin(ωt + φ0))t’ = Qmaxωcos(ωt + φ0). При этом Qmaxω ― максимальная сила тока в цепи: Imax = Qmaxω.

Сила тока в цепи переменного тока равна I = Imaxcos(ωt + φ0), где

Imax ― максимальная сила тока в цепи, [A];

ω ― циклическая частота колебаний [рад/с];

φ0 ― начальная фаза колебаний, [рад];

В колебательном контуре происходит трансформация энергии электрического поля в энергию магнитного поля.

Энергия электрического поля заряженного конденсатора равна We = = = , где

We ― энергия электрического поля конденсатора, [Дж];

C ― электроемкость конденсатора, [Ф];

U ― напряжение на обкладках конденсатора, [В];

q ― заряд на обкладках конденсатора, [Кл].

Так как напряжение на обкладках конденсатора в цепи переменного тока величина переменная, то и энергия электрического поля конденсатора ― переменна.

Энергия электрического поля конденсатора всегда положительна.

Энергия магнитного поля индукционной катушки равна Wm = , где

Wm ― энергия магнитного поля индукционной катушки, [Дж];

L ― индуктивность катушки, [Гн];

Как видно из формулы, энергия магнитного поля катушка также всегда положительна ― вне зависимости от того, какое из направлений силы тока принято в качестве положительного, а какое ― в качестве отрицательно, сила тока, возведенная в квадрат, всегда будет положительной величиной.

Согласно закону сохранения энергии, полная энергия колебательного контура постоянна в любой момент времени: W = Wm max = We max = We + Wm, где

W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];

Wm max ― максимальная энергия магнитного поля катушки индуктивности, [Дж];

We max ― максимальная энергия электрического поля конденсатора, [Дж];

Wm ― энергия магнитного поля катушки индуктивности, [Дж];

We ― энергия электрического поля конденсатора, [Дж];

или W = CU^2/2 + LI^2/2, где

W ― полная энергия свободных электромагнитных колебаний, W = const, [Дж];

C ― электроемкость конденсатора, [Ф];

U ― напряжение на обкладках конденсатора, [В];

Umax ― максимальное напряжение на обкладках конденсатора, [В];

L ― индуктивность катушки, [Гн];

I ― сила тока в катушке индуктивности, [А];

Imax ― максимальная сила тока в катушке индуктивности, [A].

Частота колебаний силы тока и напряжения в колебательном контуре определяются формулой Томпсона и зависят только от индуктивности катушки и электроемкости конденсатора. Частота и период гармонических колебаний в колебательном контуре равны v = и T = 2π√LC, где

L ― индуктивность катушки [Гн];

С ― электроёмкость конденсатора [Ф].

Принцип действия колебательного контура

Давайте рассмотрим пример, когда сначала мы заряжаем конденсатор и замыкаем цепь. После этого в цепи начинает течь синусоидальный электрический ток. Конденсатор разряжается через катушку. В катушке при протекании через нее тока возникает ЭДС самоиндукции, направленная в сторону, противоположную току конденсатора.

Разрядившись окончательно, конденсатор благодаря энергии ЭДС катушки, которая в этот момент будет максимальна, начнет заряжаться вновь, но только в обратной полярности.

Колебания, которые происходят в контуре – свободные затухающие колебания. То есть без дополнительной подачи энергии колебания в любом реальном колебательном контуре рано или поздно прекратятся, как и любые колебания в природе.

Это обусловлено тем, что контур состоит из реальных материалов (конденсатор, катушка, провода), обладающих таким свойством, как электрическое сопротивление, и потери энергии в реальном колебательном контуре неизбежны. В противном случае это нехитрое устройство могло бы стать вечным двигателем, существование которого, как известно, невозможно.

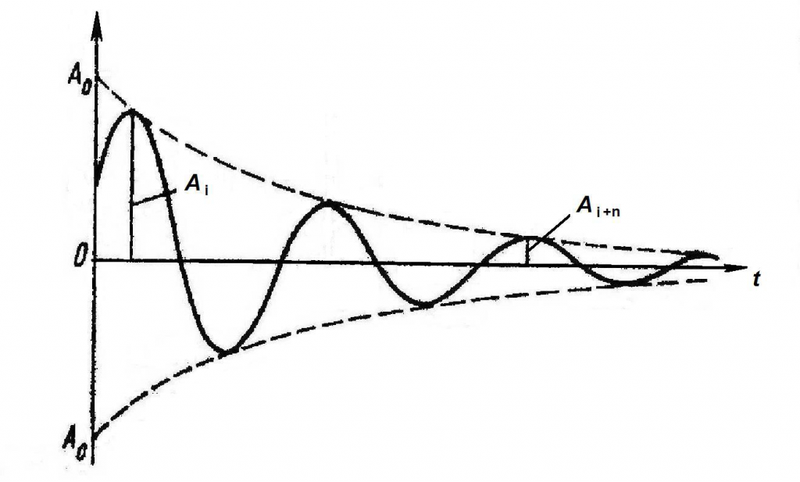
Еще одна важная характеристика LC-контура – добротность Q. Добротность определяет амплитуду резонанса и показывает, во сколько раз запасы энергии в контуре превышают потери энергии за один период колебаний. Чем выше добротность системы, тем медленнее будут затухать колебания.

Резонанс LC-контура

Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).

Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:

Электромагнитные волны

В курсе школьной физики 8-го класса вы изучали отдельно главы про электричество и магнетизм, и только в 9–10-х классах узнали, что такое разделение не совсем верно. Дело в том, что электричество и магнетизм — две стороны одной монеты, они не могут существовать друг без друга. Движущееся электрическое поле порождает магнитное, а движущееся магнитное поле порождает электрическое. Эти поля распространяются в пространстве одновременно и, что удивительно, в разных плоскостях. Взгляните на рисунок!

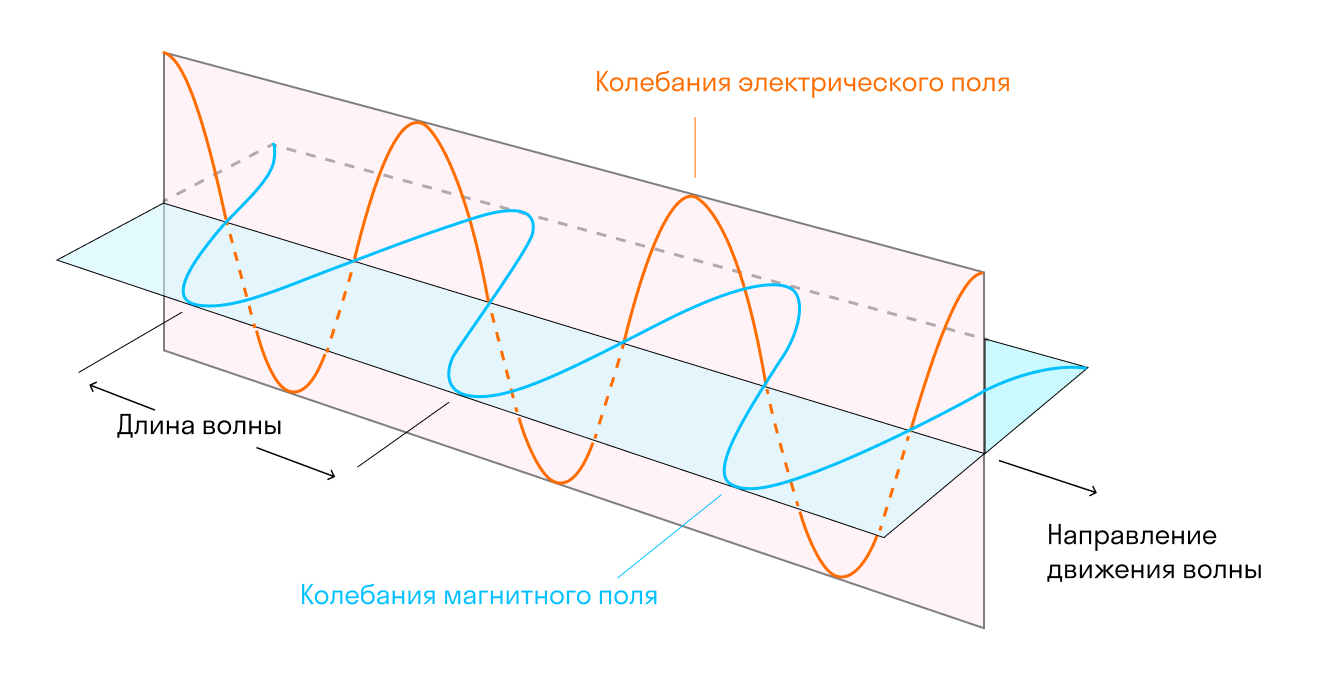
Электромагнитные волны — это распространение в пространстве с течением времени переменных (вихревых) электрических и магнитных полей.

Вихревым электрическим полем называется поле, силовые линии которого представляют собой замкнутые линии.

В разрезе этой темы стоит запомнить две фамилии: Максвелл и Герц. Вот увидите, как сойдёт с ума от счастья учитель физики, когда вы их назовёте. Джеймс Максвелл описал основные положения электромагнитной теории, а Генрих Герц доказал существование электромагнитных волн опытным путём.

К электромагнитным волнам относятся радио, Wi-Fi и даже свет. Более подробно об этом можно прочесть в нашей статье.

Что такое колебательный контур?

Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.

Также можно сказать, что колебательный контур — это электрическая цепь, работа которой порождает электромагнитное поле.

Но зачем кому-то создавать такие колебания?

Колебательные контуры — неотъемлемая часть многих производственных процессов. С их помощью изготавливают радиоприёмники, генераторы сигналов, блоки измерения частоты, контроллеры частоты напряжения на двигателях.

Возможно, вам может показаться, что это устройство давно устарело и используется в каких-то непонятных вещах, но стоит понимать, что без них не было бы возможно создание домофона, электромагнитов, различных датчиков, с которыми мы встречаемся ежедневно.

Колебательный контур состоит из двух компонентов: катушки и конденсатора, и выглядит вот так:

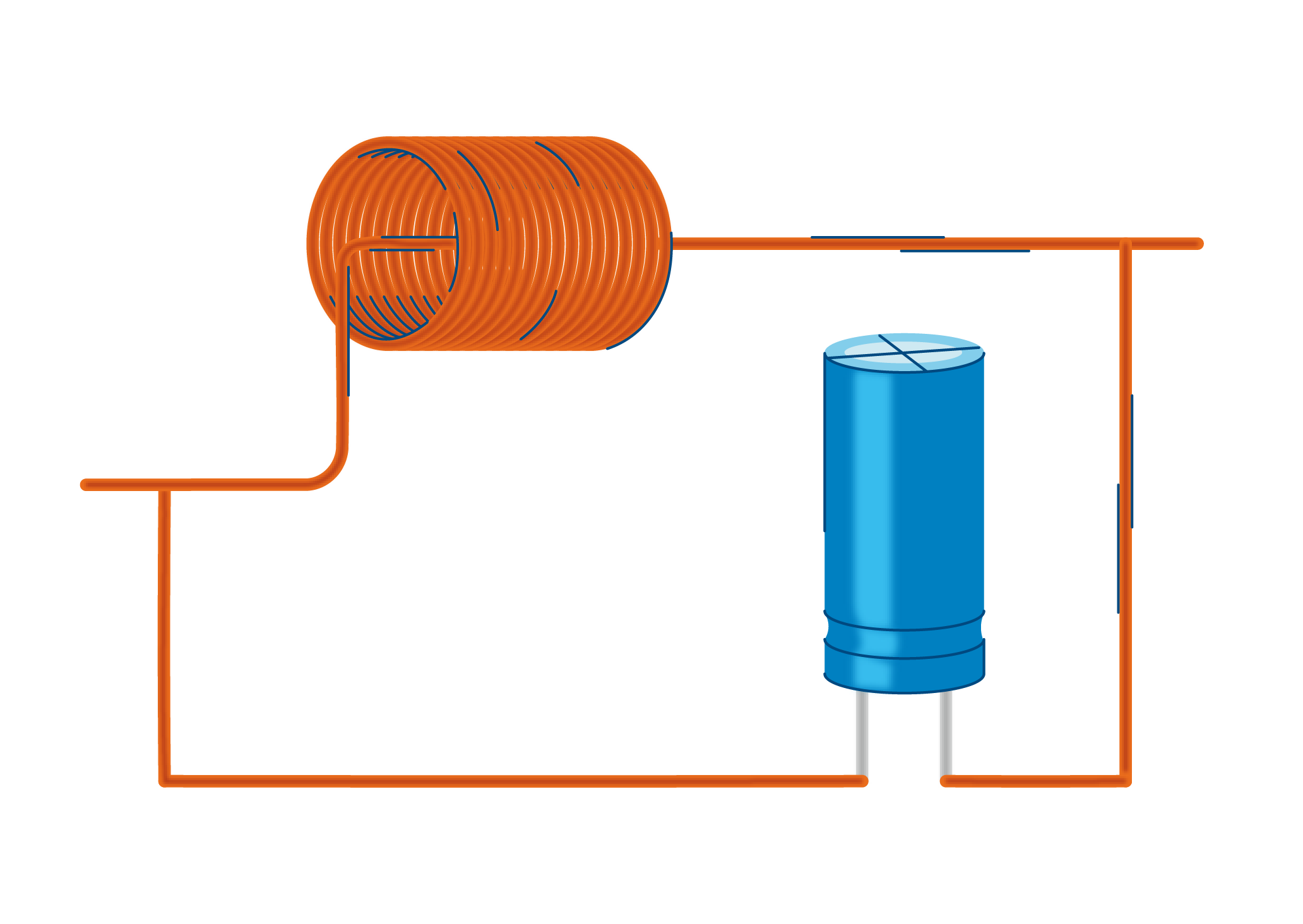
Катушка индуктивности (или соленоид) — это стержень с несколькими слоями обмотки медной проволокой. Именно он создаёт колебания в колебательном контуре. Стержень, находящийся в середине катушки, называется дроссель, или сердечник.

Катушка способна создавать колебания, только если есть электрический заряд. Она обладает низким сопротивлением.

Конденсатор — это элемент, способный накопить в себе большое количество электрического заряда. Он состоит из двух обкладок, между которыми находится диэлектрик (вещество, не проводящее электрический ток).

В чём его отличие от обычного аккумулятора? В аккумуляторе происходит превращение механической, химической, световой и других энергий в электрическую, в конденсаторе же накапливается заряд, который он может отдать весь сразу.

Часто в электрическую цепь колебательного контура подключают ещё один элемент — резистор, который обладает сопротивлением и контролирует силу тока и напряжение в цепи.

Колебательный контур

Процессы в колебательном контуре У заряженного конденсатора на одной пластине находится определенное количество отрицательного заряда, а на другой ― положительного. Поскольку между пластинами конденсатора расположен диэлектрик (или воздух, и пластины не соприкасаются) ― заряд не может прямо перейти из одной пластины на другую. Но как только такой конденсатор оказывается подключенным к проводящей цепи, один конец которой связан с одной пластиной ― а другой с другой, заряды начинают переходить от пластины к пластине по «длинному пути» ― через всю цепь. Постепенно конденсатор разряжается ― теряет заряд, а в цепи наблюдается ток, ведь ток ― это направленные движения зарядов.

Но разряженный конденсатор больше не может поддерживать силу току ― ведь заряда на его обкладках нет, и не будь в цепи катушки индукции, ток бы прекратился. Однако здесь вновь срабатывает правило Ленца: после того как сила тока достигла максимума и начала уменьшаться ― в катушке возникает ЭДС и индукционные токи, которые стремятся вернуть силу тока такой, как она была ― максимальной. Поэтому, даже после того, как конденсатор разряжен, в цепи продолжает течь ток. Заряды попадают на обкладку конденсатора и постепенно заряжают ее. На этот раз, та обкладка конденсатора, которая была заряжена положительно и принимала заряд, начинает накапливать отрицательный заряд, а так обкладка, которая была заряжена отрицательно, становится заряженной положительно.

После того как конденсатор зарядиться ― он вновь начинает разряжаться. Таким образом, в контуре происходят колебания заряда, силы тока, напряжения и энергий магнитного и электрического поля в катушке индуктивности и конденсаторе.

Виды колебательных контуров

Последовательный колебательный контур

Последовательный колебательный контур состоит из катушки индуктивности, конденсатора и сопротивления, которые соединены последовательно друг с другом. В этом типе контура ток проходит через каждый элемент по очереди.

В последовательном колебательном контуре резонансная частота определяется формулой:

fрез = 1 / (2π√(LC))

где fрез – резонансная частота, L – индуктивность катушки, C – емкость конденсатора.

Параллельный колебательный контур

Параллельный колебательный контур состоит из катушки индуктивности, конденсатора и сопротивления, которые соединены параллельно друг другу. В этом типе контура напряжение одинаково на каждом элементе.

В параллельном колебательном контуре резонансная частота определяется формулой:

fрез = 1 / (2π√(LC))

где fрез – резонансная частота, L – индуктивность катушки, C – емкость конденсатора.

Частотная характеристика колебательного контура

Резонансная частота

Резонансная частота – это частота, при которой колебательный контур находится в резонансе, то есть достигает максимальной амплитуды колебаний. Для последовательного и параллельного колебательных контуров резонансная частота определяется одной и той же формулой:

fрез = 1 / (2π√(LC))

где fрез – резонансная частота, L – индуктивность катушки, C – емкость конденсатора.

Полоса пропускания

Полоса пропускания – это диапазон частот, в котором колебательный контур пропускает сигналы с минимальными потерями. Она определяется разностью между верхней и нижней частотами, на которых амплитуда сигнала уменьшается на 3 дБ (половина от максимальной амплитуды).

Для последовательного колебательного контура полоса пропускания может быть рассчитана по формуле:

BW = 1 / (2πRC)

где BW – полоса пропускания, R – сопротивление, C – емкость конденсатора.

Для параллельного колебательного контура полоса пропускания может быть рассчитана по формуле:

BW = 1 / (2πL/R)

где BW – полоса пропускания, L – индуктивность катушки, R – сопротивление.

Фазовый сдвиг

Фазовый сдвиг – это разность фаз между входным и выходным сигналами колебательного контура. Он зависит от частоты сигнала и может быть как положительным, так и отрицательным.

На резонансной частоте фазовый сдвиг для последовательного колебательного контура равен 0°, а для параллельного колебательного контура – 180°.

Колебательный контур

Колебательным контуром называется цепь из параллельно соединенных конденсатора и катушки индуктивности.

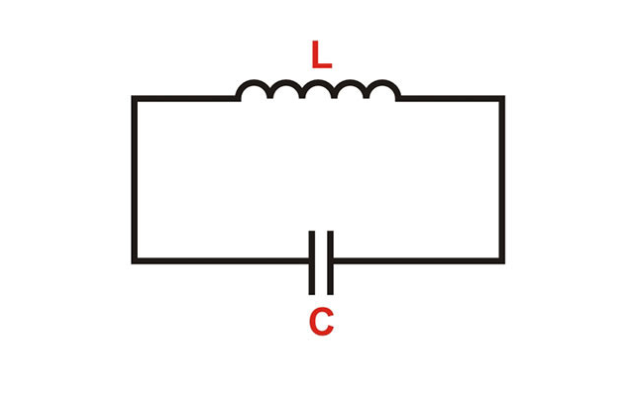
Разорвем схему, и зарядим конденсатор. На его обкладках появится напряжение. Если теперь соединить выводы конденсатора внешним проводником – возникнет сильный электрический разряд, поскольку сопротивление проводника невелико, ток разряда резко возрастет до больших значений, выделяемая мощность также будет велика.

Однако, если замкнуть контур через катушку индуктивности, ситуация будет иной. Электрическое сопротивление катушки также невелико, однако, резкого броска тока не возникнет. Происходящее дальше будет состоять из двух стадий.

Первая стадия

Конденсатор начнет разряжаться через малое сопротивление катушки. Но, в результате явления самоиндукции, возникающее в катушке магнитное поле будет направлено так, чтобы противодействовать причине, его вызывающей. Поэтому ток будет возрастать гораздо медленнее, чем при коротком замыкании. Напряжение на конденсаторе при этом будет падать. В результате максимальное значение тока не достигнет значений короткого замыкания.

В конце стадии разряда конденсатора ток через обе компоненты контура будет иметь некоторое максимальное значение, а напряжение на конденсаторе уменьшится до нуля.

Вторая стадия

Здесь опять ключевую роль играет явление самоиндукции. Поскольку напряжение на обоих компонентах контура уменьшилось до нуля, ток должен прекратиться. Однако, магнитный поток в катушке индуктивности направлен так, чтобы противодействовать этому. В результате ток исчезает не сразу, а снижается в течение некоторого времени.

Снижающийся ток проходит через разряженный конденсатор, и заряжает его (уже в противоположном направлении). И к моменту полного снижения тока до нуля конденсатор оказывается заряжен снова.

Формула Томсона

Для получения формулы колебательного контура необходимо учесть, что энергия в нем существует в двух формах:

в форме заряда конденсатора: $W_C=$
в форме магнитного поля катушки: $W_L=$

Сумма этих величин будет постоянна: $W_C+W_C=const$. Если теперь вычислить скорость изменения каждого вида энергии (взяв производные по времени) и приравнять их друг другу, то после преобразований можно получить формулу, позволяющую произвести расчет частоты колебаний в контуре:

Или для периода колебаний:

Данная формула называется формулой Томсона в честь физика, который ее вывел.

Расстройка устройства

Расстройка — это настройка контура на частоту, отличную от резонансной. Последняя наступает в том случае, когда характеристики частот радиодетали и генератора совпадают. В некоторых устройствах этого необходимо избегать. Чтобы получить резонанс, нужно воспользоваться одним из трех методов изменения характеристик:

частоты генератора;
индуктивности;
емкости.

Два последних метода можно делать одновременно для достижения лучшего эффекта. Расстройки классифицируются на три вида: абсолютную, обобщенную и относительную. Первой называется разность между частотами контура и резонанса. Обобщенная вычисляется при помощи отношения реактивного сопротивления к активному. Относительная выражается в виде отношения абсолютной расстройки к резонансной частоте.

Кроме того, расстройка бывает положительной и отрицательной. В первом случае необходимо, чтобы частота генератора была больше частоты контура. Для отрицательной должно соблюдаться другое условие: частота генератора меньше, чем у контура.

В некоторых случаях необходимо убрать резонансную частоту. Выполняется такая операция при помощи изменения необходимых характеристик электроцепи «контур — генератор». Очень часто в контуре применяются конденсаторы с переменной емкостью, позволяющие настраивать его. Настройка конденсатора происходит благодаря изменению расстояния между его обкладками. Этот принцип очень удобен, поскольку для изменения индуктивности катушки необходим сердечник, который будет выкручиваться.

Однако существуют радиоэлементы и такого типа. В них емкость является постоянной величиной, а индуктивность изменяется с помощью сердечника. Конструктивная особенность последнего представляет обыкновенный ферритовый болт, который вкручивается в пластиковый корпус. На последний наматывается провод.

Пример решения

Для устройства нужно произвести расчет контура с частотой резонанса 1 МГц. Можно воспользоваться описанными формулами, однако радиолюбители произвели некоторые вычисления и предложили более упрощенный вариант: L = (159,1 / f)^2 / C. Для контура можно взять приближенное значение емкости плоского конденсатора, равное 1000 пкФ. На корпусе указывается этот параметр.

Кроме того, маркировка может содержать напряжение, на которое он рассчитан. Подставив все значения в формулу, можно узнать индуктивность: L = (159,1 / 1)^2 / 1000 = 25 (мкГн). После этого следует вычислить количество витков N катушки с диаметром каркаса D по такому соотношению: N = 32 * [L / D]^(½). Если предположить, что D = 5 мм (можно взять со старых контуров), то N = 32 * [25 / 5]^(½) = 72 (витка). Однако за основу можно взять катушку с подстроечным ферритовым сердечником со следующими параметрами:

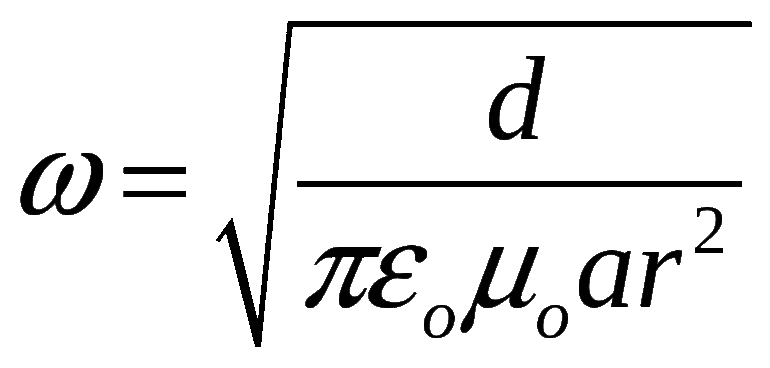
длина — 13—15 мм;
диаметр — 2,3—3,2 мм.

Можно воспользоваться таким соотношением: N = 8,5 * L^(½) = 8,5 * 25^(½) = 43 (витка). Провод следует брать 0,1 мм в диаметре. Это показатель измеряется при помощи штангенциркуля.

Таким образом, колебательный контур является простейшей системой для генерации электромагнитных колебаний, затухание которых зависит от частоты резонанса и добротности радиоэлемента.