Какой буквой обозначается емкость конденсатора

Содержание

Ток — это направленное движение заряженных частиц. Ток в проводниках создается перемещением электронов, так как они могут двигаться в материале свободно, в отличие от зафиксированных в узлах решеток атомов.

Сила тока равна величине заряда, проходящего в единицу времени через проводник (I = frac) , где:

(I) — сила тока, (lbrack Arbrack) ;

(q) — перемещенный через проводник заряд, (lbrack Клrbrack) ;

(t) — время перемещения заряда, (lbrack сrbrack) ;

Проводник, через который проходит заряд, оказывает определенное сопротивление перемещению этого заряда. Связь между разностью потенциалов на концах проводника (напряжением), силой тока в участке цепи, и сопротивлением цепи носит название закона Ома.

Закон Ома для участка цепи имеет вид

(I) — сила тока (lbrack Arbrack) ;

(U) — напряжение (разность потенциалов) (lbrack Brbrack) ;

(R) — сопротивление (lbrack Омrbrack) ;

Сопротивление проводника — это его физическая характеристика, не зависящая от силы тока в цепи или напряжения, и зависящая только от размеров проводника и материала из которого он изготовлен.

Сопротивление проводника равно (R = frac>) , где

(R) — сопротивление (lbrack Омrbrack) ;

(I) — длина проводника (lbrack мrbrack) ;

(rho) — удельное сопротивление проводника (lbrack Ом cdot мrbrack) ;

(S) — площадь поперечного сечения проводника (lbrack м^rbrack)

Параллельное и последовательное соединение проводников.

При последовательном соединении общее сопротивление равно сумме сопротивлений всех источников сопротивления (R = R_ + R_ + R_ + ldots + R_ + R_) , где

R — общее сопротивление всех источников сопротивления, (lbrack Омrbrack)

сопротивление каждого из источников сопротивления в цепи, (lbrack Омrbrack)

(n) — количество всех источников сопротивления в цепи.

Сила тока на каждом из источников сопротивления при последовательном соединении, и общая сила тока на участке цепи, одинаковы ( I = I_ = I_ = I_ = ldots = I_ = I_) , где

(I) — сила тока на участке цепи, (lbrack Arbrack)

(I_,I_,I_,ldots,I_,I_ -) сила тока на каждом из источников сопротивления в цепи, (lbrack Arbrack)

Напряжение в участке цепи равно сумме напряжений на каждом из источников сопротивления

(U = U_ + U_ + U_ + ldots + U_ + U_) , где

(U) — напряжение на участке цепи, (lbrack Brbrack)

(U_,U_,U_,ldots,U_,U_ -) напряжение на каждом из источников сопротивления в цепи, (lbrack Brbrack)

При параллельном соединении общее сопротивление источников сопротивления вычисляется как (frac = frac + frac> + frac> + ldots + frac> + frac>) .

Общее сопротивление двух параллельно соединенных резисторов равно

Сила тока в цепи при параллельном соединении равна (I = I_ + I_ + I_ + ldots + I_ + I_) .

Напряжение в цепи и на каждом из источников сопротивления одинаковы ( U = U_ = U_ = U_ = ldots = U_ = U_) .

Заряженные частицы в цепи всегда стремятся перемещаться по пути наименьшего сопротивления. Если хотя бы одна из ветвей цепи не нагружена сопротивлением — то весь ток будет перемещаться по ней. На рисунке показан пример цепи, у которой одна из ветвей — верхняя — не имеет сопротивления. Именно по ней пройдет весь ток, а общее сопротивление цепи будет равно нулю.

Конденсатор

Основная характеристика конденсатора — электроемкость или просто емкость С, определяемая как отношение заряда одной из обкладок конденсатора к разности потенциалов, т.е. напряжению между обкладками:

где (C) — емкость конденсатора (lbrack Фrbrack) ;

(q) — заряд одной из обкладок конденсатора (lbrack Клrbrack) ;

(U) — напряжение между обкладками (lbrack Brbrack) .

При этом в емкость конденсатора не зависит от его заряда и определяется только его геометрическими параметрами (формой, размером и расстоянием между обкладками) и характеристиками материала, которым заполнено пространство между обкладками конденсатора. Напряжение (разность потенциалов) между обкладками будет устанавливаться в зависимости от того заряда, который сообщен конденсатору.

Единицы емкости. В СИ за единицу электроемкости принят фарад (Ф). Емкостью 1 Ф обладает конденсатор, между обкладками которого устанавливается напряжение в 1В при сообщении ему заряда 1 Кл:

На практике обычно приходится иметь дело с конденсаторами, емкость которых значительно меньше 1 Ф, поэтому используются доли этой единицы — микрофарад (мкФ), пикофарад (пФ): 1мкФ = 10 -6 Ф, 1пФ = 10 -6 мкФ = 10 -12 Ф.

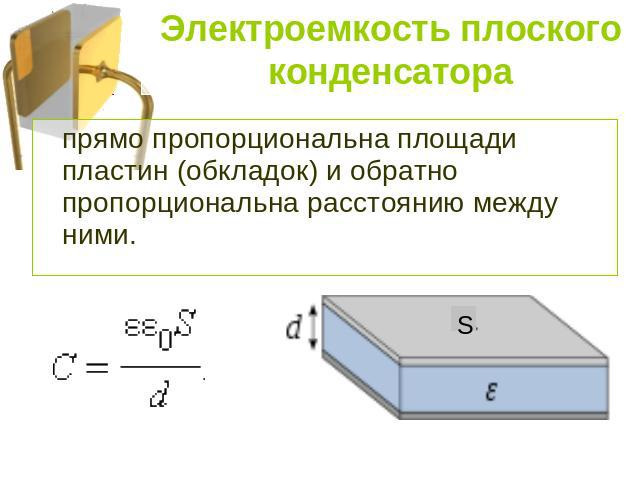
Емкость плоского конденсатора.

Простейший конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским.

Его емкость рассчитывается по следующей формуле:

где (C) — емкость конденсатора (leftlbrack Ф rightrbrack) ;

(varepsilon ₀) — электрическая постоянная , (( approx 8,85 bullet 10^fracА^> Кг>))

(varepsilon) — диэлектрическая проницаемость;

(S) — площадь обкладки (lbrack м^rbrack) ;

(d) — расстояние между обкладками (lbrack мrbrack) .

Пространство между обкладками конденсатора может быть заполнено любым диэлектриком (веществом, не проводящим электрический ток). Диэлектрики характеризуются величиной, называемой диэлектрической проницаемостью.

Диэлектрическая проницаемость (varepsilon) — это безразмерная величина, показывающая во сколько раз напряженность электрического поля (или напряжение между его обкладками) в заполненном диэлектриком конденсаторе меньше, чем в отсутствии диэлектрика при том же заряде конденсатора. Другими словами, диэлектрическая проницаемость показывает, во сколько раз увеличится емкость конденсатора при заполнении его диэлектриком.

У твердых диэлектриков значение ε лежит в пределах от 4 до 7, а для жидких — от 2 до 81.

Электроемкость. Конденсаторы

Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q 1 и q 2 ), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δ φ . Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U .

В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).

Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.

Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.

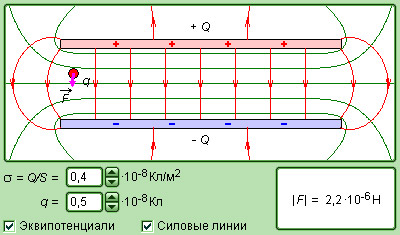
Рисунок 1 . 6 . 5 . Смоделированное электрическое поле плоского конденсатора.

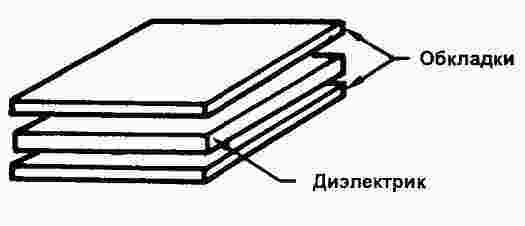
Устройство простейшего конденсатора

Конденсатор состоит их двух металлических пластин — электродов, называемых также обкладками, между которыми находится тонкий слой диэлектрика.

Собственно, все конденсаторы устроены именно таким (или почти таким) образом, разве что меняется материал обкладок и диэлектрика.

Чтобы увеличить ёмкость конденсатора, не увеличивая его размеры, применяют разные хитрости. Например, если мы возьмем две обкладки в виде длинных полосок фольги, проложим между ними хотя бы тот же полиэтилен и свернем все это как рулет, то получится очень компактный прибор с большой ёмкостью. Именно так устроены плёночные конденсаторы.

Если вместо полиэтилена взять бумагу и пропитать её электролитом, то на поверхности фольги образуется тонкий слой оксида, который не проводит ток. Такой конденсатор будет называться электролитическим.

Существует много разных видов конденсаторов: бумажные, плёночные, оксидные алюминиевые и танталовые, вакуумные и т.п. В нашем уроке мы будем использовать оксидные электролитические конденсаторы из-за их большой ёмкости и доступности.

Полярные и неполярные конденсаторы

Очень важным является разделение конденсаторов на полярные и неполярные.

Приборы на основе оксидов: электролитические алюминиевые и танталовые обычно являются полярными, а значит если перепутать их полярность — они выйдут из строя. Причём этот выход из строя будет сопровождаться бурной электрохимической реакций вплоть до взрыва конденсатора.

На полярных конденсаторах всегда имеется маркировка. Как правило на электролитических конденсаторах на корпусе контрастной полосой отмечается отрицательный вывод (катод), у танталовых (в желтых прямоугольных корпусах) полоской помечается положительный вывод (анод). Если есть сомнения в маркировке, то лучше найти документацию на этот конденсатор и убедиться.

Неполярные же конденсаторы можно включать в цепь какой угодно стороной. К примеру, многослойные керамические конденсаторы — неполярные.

Основы автоэлектрики. Часть5. Электрическая ёмкость и конденсаторы

Сегодня мы коснёмся темы накопителей заряда, именуемых конденсаторами.

Конденсатор — пассивный электронный компонент, состоящий из двух полюсов, накапливающий заряд.

Электрическая ёмкость — это отношение электрического заряда к разности потенциалов между полюсами конденсатора (или иного другого электронного компонента). Единица измерения — Фарад и его производные (пикоФарад, наноФарад, микроФарад). Обозначается ёмкость латинской буквой С.

Мы уже обсуждали, что ток — это есть скорость перемещения заряда, а напряжение — это разность потенциалов. Мы всегда удобно проводить некие параллели, поэтому напряжение ассоциируется с разницей давления в жидкости или газе, а ток — с объёмной скоростью жидкости или газа. Поэтому конденсатор можно представить себе как некий сосуд, который наполняют жидкостью или газом давлением, которое выше чем в сосуде. Наполнение сосуда будет происходить до тех пор, пока давление подачи не уровняется с давлением в сосуде. Так и работает конденсатор: по мере наполнения зарядом растет напряжение. Чем ближе будет напряжение в конденсаторе к напряжению заряжающего источника, тем меньше будет скорость заряда. Это аналогично тому, как наполняется сосуд. Если мы заполнили сосуд, затем открыли кран у него — ток начинает утекать, тем самым снижая количество заряда и понижая напряжение.

Если рассматривать провод или резистор как трубу, а конденсатор — как сосуд, многое становится понятно на интуитивном уровне. Ну, и проще понять реактивные сопротивления, о которых мы говорили ранее. Но надо понимать, что сосуд — это сосуд, а конденсатор — это конденсатор=)

Итак, в простейшем виде конденсатор представляет собой две параллельные пластины, между которыми находится некий диэлектрик. Самый простой диэлектрик — это воздух. Конечно, сегодня воздушные конденсаторы уже и не встретить, но я ещё несколько лет назад использовал переменный воздушный конденсатор для сборки радиоприёмника=) Правда, в этом конденсаторе пластин было гораздо больше двух, и выглядел примерно вот так:

Вращая ручку, можно было изменять значение электрической ёмкости.

На, а вот так обычно представляют простейший конденсатор:

В случае такого конденсатора ёмкость вычисляется следующим образом:

Сегодня конденсаторов огромное множество. Наиболее популярные — керамические, электролитические и танталовые. Отличие последних двух в том, что они полярны, и крайне не рекомендую включать их в схему обратной полярностью=)

Основными параметрами конденсатора являются:
— Электрическая ёмкость,
— Максимально допустимое напряжение на его обкладках (немаловажный параметр, при подачи бОльшего напряжения можно увидеть много весёлых, но крайне не безопасных эффектов:-), особенно на конденсаторах большой ёмкости),
— Полярность (т.е. полярный или неполярный),
— Допустимые отклонения от номинального значения ёмкости (обычно в процентах),
— Диапазон рабочих температур,
— Тип корпуса.

Полярность, допустимые отклонения и диапазон температур напрямую зависят от применяемого диэлектрика. Как правило, конденсаторы большой ёмкости — электролитические, т.е. в качестве диэлектрика — электролит. А электролитические конденсаторы по физике процессов сильно напоминают всем знакомые свинцово-кислотные аккумуляторы и аналогично им имеют полярность, что приводит к некоторым ограничениям. Кроме того, они имеют свойство высыхать. И именно они являются частой причиной выхода из строя бытовой и промышленной электроники, в результате чего страдают и иные компоненты. Выглядят электролитические конденсаторы так:

Танталовые конденсаторы были некогда призваны заменить электролитические, но и те имеют ряд ограничений и так и не достигли приличных ёмкостей. Кроме того, взрываются они не менее весело=) Выглядят они вот так:

Спешу обрадовать, что развитие электроники не стоит на месте и сегодня вполне можно приобрести обычные керамические конденсаторы с ёмкостью, сравнимой с танталовыми, а некоторые достигают ёмкости 330 мкФ при допустимом напряжении в 4 В. И это всё в малом чип-корпусе 1206!
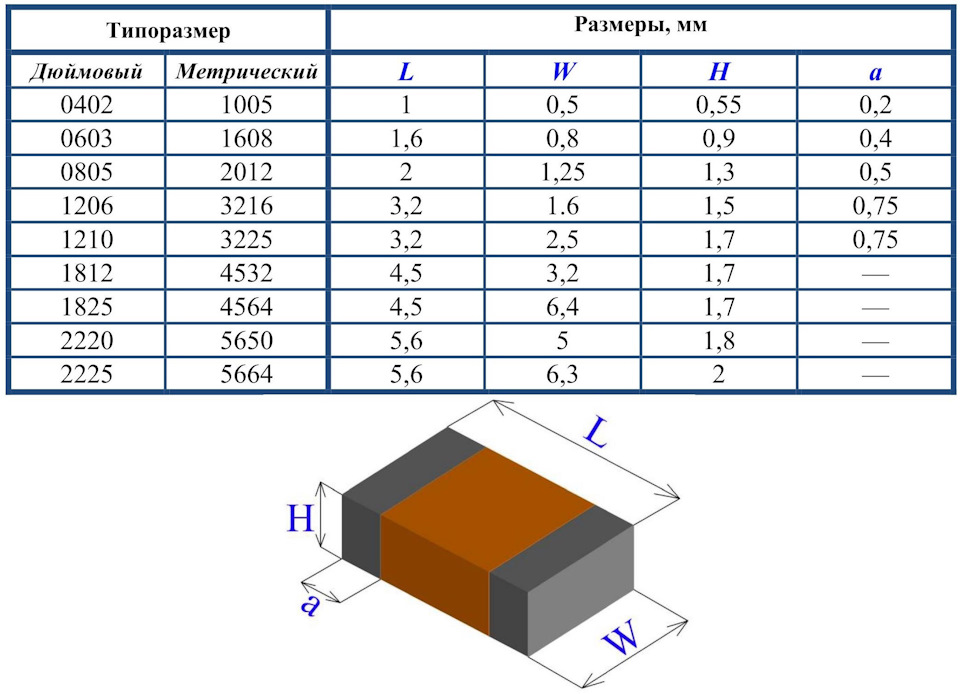
Кстати, размеры основных корпусов чип-конденсаторов:

Ну, и не все конденсаторы в чипах, поэтому существуют и выводные конденсаторы:

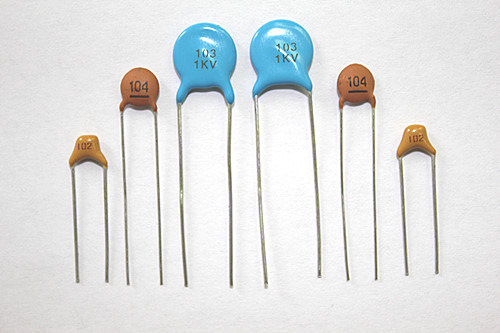
Причина такому прорыву — отличный диэлектрик под кодовым названием X5R. 330 мкФ при 4В — не густо конечно. Но на большие напряжения ёмкости также достигли впечатляющих значений — на те же 16В найти 100 мкФ не проблема, на 25 В — на 22 мкФ, на 35-50 В пока не больше 10 мкФ. Тем не менее, во многих и многих приложениях электроники появляется возможность отказаться от электролитов и танталов.

Вернемся к основным свойствам. Если рассматривать глубже, то параметров конденсаторов гораздо больше:
— Температурная зависимость параметров,
— Входное сопротивление (ESR),
— Внутреннее сопротивление,
— Время наработки на отказ (очень интересный параметр, которому реально посвятить целую статью),
— многие другие.

Расписывать здесь все детали не вижу смысла, так эти параметры важны тем, кто глубоко занимается электроникой. Тем не менее счел важным упомянуть о них. Кому захочется капнуть — можно порыться в сети.

Помимо указанных выше конденсаторов следует немного сказать о плёночных конденсаторах. Выглядят они вот так:

Их основное отличие от предыдущих — это поражающая надежность и способность работать в силовых цепях, особенно в цепях с высоким напряжением.

Наверное, сегодня краткого обзора будет достаточно. О применении конденсаторов поговорим в следующих статьях.

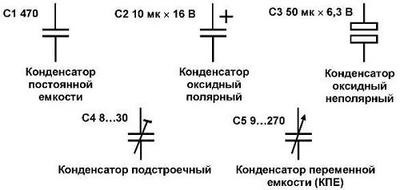
В прошлой статье писал, но и здесь напомню, что конденсаторы на схемах обозначаются так:

На сим всё;)
Продолжение следует=)
___________________________________________________________________________

Конденсатор переменной емкости

Конденсаторы, емкость которых можно менять, называются конденсаторами переменной емкости.

Наиболее простой конденсатор переменной емкости имеет несколько (реже один) медных или алюминиевых полудисков, соединенных между собой электрически и укрепленных неподвижно. Другой ряд таких же полудисков собран на общей оси. При повороте этой оси каждый из укрепленных на ней полудисков входит меду двумя неподвижными полудисками. Поворачивая ось и меняя таким образом взаимное расположение подвижных и неподвижных полудисков, мы можем менять емкость конденсатора. На рисунке 3 показана схема устройства и на рисунке 4 – общий вид воздушного конденсатора переменной емкости.

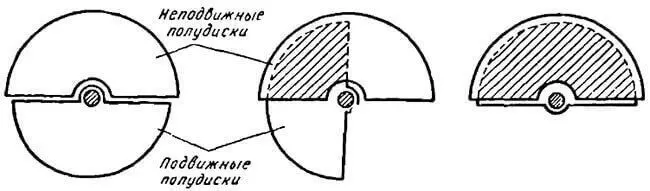
Рисунок 3. Схема устройства конденсатора переменной емкости

Рисунок 4. Общий вид конденсатора переменной емкости

Видео об устройстве серийного конденсатора переменной емкости:

Видео о том, как можно сделать самодельный конденсатор переменной емкости своими руками:

Электролитические конденсаторы

В радиотехнике применяются также электролитические конденсаторы. Эти конденсаторы изготовляются двух типов: жидкостные и сухие. В обоих типах конденсаторов употребляется оксидированный алюминий. Путем специальной электрохимической обработки на поверхности алюминия получают тонкий (порядка нескольких десятков микрон) слой оксида алюминия Al2O3, представляющий так называемую оксидную изоляцию алюминия. Оксидная изоляция обладает электроизолирующими свойствами, а также является механически прочной, нагревостойкой, но гигроскопичной.

В жидкостных электролитических конденсаторах алюминиевую оксидированную пластину помещают внутрь металлического корпуса, который служит второй пластиной. В корпус заливают электролит, состоящий из раствора борной кислоты с некоторыми примесями.

Сухие электролитические конденсаторы изготовляют путем сворачивания трех лент. Одна лента представляет собой алюминиевую оксидированную фольгу (тонко раскатанный лист металла). Другой пластиной является лента из алюминиевой фольги. Между двумя металлическими лентами помещается бумажная или марлевая лента, пропитанная вязким электролитом. Плотно свернутые ленты помещаются в алюминиевый корпус и заливаются битумом. Тонкий оксидный изолирующий слой с высокой электрической проницаемостью (ε = 9) позволяет получить дешевые конденсаторы с большой удельной емкостью.

Видео об устройстве электролитического конденсатора:

Ликбез КО. Лекция №2 Конденсатор.

Конденсатор (ёмкость)
Конденсатор (ёмкость) –элемент, способный накапливать электромагнитную энергию в собственном электрическом поле, образуемом обкладками конденсатора. Обозначается – С. Напряжение и ток на его контактах связано зависимостью:

Величина ёмкости измеряется в фарадах (Ф). 1 фарада – это величина такой ёмкости, на которой имеет место падение напряжения 1 вольт при наличии заряда в ёмкости 1 кулон.

10 июля 2013, среда 12:41

OQtagooi [ ] для раздела Блоги

1 фарада – очень большая величина, поэтому применяемые в технике конденсаторы имеют величины: — пикофарад – 10-12; нанофарад – 10-9; микрофарад – 10-6.
Процессы, происходящие в конденсаторе на временном графике при подключении конденсатора к источнику прямоугольного однополярного сигнала, показаны на рисунке.

Из рисунка видно, что в момент подачи прямоугольного импульса источника тока (красный), напряжение на выводах конденсатора (фиолетовый) сначала равно нулю и с изменением времени увеличивается по экспоненте – конденсатор заряжается, а ток конденсатора (зелёный) наоборот сначала максимален, но потом по мере заряда уменьшается по экспоненте. При пропадании импульса, напряжение на выводах конденсатора уменьшается по экспоненте – конденсатор разряжается, а ток, изменивший полярность сначала максимален, и по мере разряда уменьшается из отрицательной области до нуля. Скорость изменения напряжения и тока зависит от значения ёмкости. Чем больше ёмкость, тем медленнее они изменяются (экспонента более вытянута по времени). Напряжение и ток на нагрузочном резисторе ведут себя одинаково, и изображены на временном графике оранжевым цветом. Их взаимосвязь описывается законом Ома.
Фактически, мы рассмотрели «четырёхполюсник» состоящий из конденсатора и резистора, который называют дифференцирующей цепочкой.

Дифференцирующая цепочка применяется для преобразования прямоугольных импульсов большой длительности в прямоугольные импульсы малой длительности. Чтобы, Вам было понятнее, дифференцирующая цепочка и преобразование импульса изображены на следующем рисунке.

Вслед за дифференцирующей цепочкой устанавливается пороговое устройство, не пропускающее через себя всё, что ниже по амплитуде установленного порога, с выхода порогового устройства, срезанные импульсы поступают на усилитель-ограничитель, который усиливает «кривой» импульс и ограничивая его амплитуду «сверху» пропускает его на выход.
Кроме функции преобразования прямоугольных импульсов, дифференцирующая цепочка может применяться в качестве фильтра высоких частот (ФВЧ). Конденсатор – инертный элемент. Если к конденсатору с большой ёмкостью приложить переменное напряжение низкой частоты, в силу своей инертности, ёмкость будет не способной пропустить через себя ток, ведь конденсатору сначала надо будет зарядиться, а потом отдавать заряд. Свойство конденсатора сопротивляться переменному электрическому току называют реактивным сопротивлением конденсатора, которое используется при конструировании частотных фильтров и колебательных контуров. Реактивное сопротивление конденсатора обозначается Xc или Zc и измеряется в Омах. Реактивное сопротивление конденсатора связано с собственной ёмкостью и частотой тока выражением:

Из формулы видно, что реактивное сопротивление конденсатора обратно пропорционально частоте. Другими словами, чем выше частота, тем меньше реактивное сопротивление конденсатора.

Теперь представьте, что дифференцирующая цепь, это – делитель напряжения, где вместо первого резистора выступает конденсатор. А мы из формулы теперь знаем, что конденсатор легко пропускает высокие частоты – его сопротивление минимально и плохо пропускает низкие частоты – его сопротивление максимально. В радиоэлектронике, когда рассчитывают частотные фильтры, то считают характеристикой фильтра – частоту среза, которая определяется как значение частоты сигнала, на котором амплитуда выходного сигнала уменьшается (затухает) до значения 0,7 от входного сигнала. Чтобы было понятнее, изображу это на рисунке.

То, что изображено, называется амплитудно-частотной характеристикой, или сокращённо — АЧХ. Для фильтра высоких частот соответствует АЧХ фиолетового цвета, и частота среза равная значению f2.

Зная, как рассчитывается делитель напряжения и реактивное сопротивление конденсатора на определённой частоте, Вы элементарно можете рассчитать простейший г-образный фильтр высокой частоты на конденсаторе и резисторе.
Если в дифференцирующей цепочке поменять местами конденсатор и резистор, то мы получим – интегрирующую цепочку. Все процессы в интегрирующей цепочке происходят точно так же, как и в дифференцирующей. Временные графики, показанные на первом рисунке абсолютно справедливы для интегрирующей цепочки. Отличие заключается в том, что выходным элементом является не резистор, а конденсатор. Поэтому, на выходе интегрирующей цепи будут не остроконечные дифференцированные импульсы (зелёного цвета), а импульсы напряжения, которое присутствует на выводах конденсатора (фиолетового цвета). Ну а если дифференцирующая цепочка – это фильтр высоких частот, то интегрирующая цепочка – это фильтр низких частот (ФНЧ). И рассчитывается он так же, через делитель напряжения. Для фильтра низких частот соответствует АЧХ на рисунке — оранжевого цвета, и частота среза равная значению f1.
Cледует добавить, частотные фильтры, выполненные на конденсаторах и резисторах имеют пологую амплитудно-частотную характеристику. Другими словами у таких фильтров слабо выражен частотный срез. Более качественный срез имеют фильтры состоящие из конденсаторов и катушек индуктивности (дросселей), но об этом позже, когда изучим катушку индуктивности.
Параллельное соединение конденсаторов
Общая ёмкость конденсаторов при параллельном соединении равна их сумме.

Последовательное соединение конденсаторов
Величина, обратно пропорциональная общей ёмкости конденсаторов при последовательном соединении равна сумме величин, обратно пропорциональных их ёмкости.

Для двух последовательно соединенных конденсаторов их общая ёмкость равна:

other_material_inline_bottom

Какой буквой обозначается емкость конденсатора

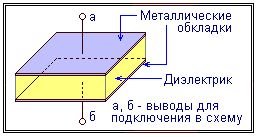
КОНДЕНСАТОР — означает накопитель. В радио и электронной аппаратуре конденсатор является накопителем электрических зарядов. Простейший конденсатор состоит из двух металлических пластинок разделенных слоем диэлектрика. Диэлектрик — это материал который не проводит электрического тока и обладает определенными свойствами о которых поговорим чуть позже.

Так как конденсатор является накопителем, то он должен обладать определенной емкостью (объемом для накопления зарядов). На емкость конденсатора влияют площадь пластин (еще их называют «обкладками»), расстояние между обкладками и качество диэлектрика. К хорошим диэлектрикам относятся вакуум, эбонит, фарфор, слюда, полиэтилен, текстолит и много других синтетических материалов.
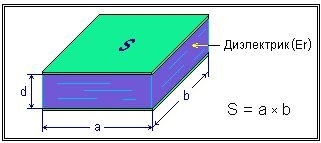
На рисунке изображен простейший конденсатор с двумя параллельными обкладками площадью S (S = m * n), которые находятся в вакууме на расстоянии d друг от друга.

Если между верхней и нижней обкладками конденсатора приложить напряжение Uab, то на верхней и нижней обкладках конденсатора накопятся одинаковые положительный +q и отрицательный -q заряды, которые называют свободными. Между обкладками возникает электрическое поле обозначенное на рисунке буквой Е.
Емкость нашего конденсатора (обозначается буквой С) будет: С = Eo*S/d, где Ео — электрическая постоянная (для вакуума) Ео=8,854 * 10 -12 Ф/м (Фарад на метр).
Если между обкладками поместить диэлектрик,

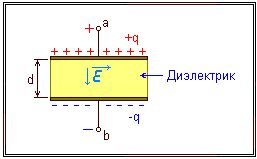
то ёмкость конденсатора будет: С = Er * Eo *S / d. В формуле расчета ёмкости добавилась величина Er — относительная диэлектрическая проницаемость введённого диэлектрика.
Из формулы следует, что емкость конденсатора увеличивается на величину Er проницаемости диэлектрика. Итак, чем больше площадь S пластин конденсатора, больше значение Er и меньше расстояние d между пластинами, тем больше емкость конденсатора. Основной единицей емкости в системе единиц СИ является фарад (Ф). Емкость 1Ф очень велика. В электротехнике обычно используют дольные единицы емкости:
микрофарада (мкФ), 1мкФ = 1*10 -6 Ф,
нанофарада (нФ), 1нФ = 1*10 -9 Ф , и
пикофарада (пФ), 1пФ = 1*10 -12 Ф.

При выборе диэлектрика для конденсаторов, кроме относительной диэлектрической проницаемости диэлектрика, учитывают еще два важных параметра:
1) Электрическую прочность — прочность диэлектрика при подаче на прокладки конденсатора высокого напряжения. При низкой электрической прочности может произойти электрический пробой, и диэлектрик станет проводником электрического тока;
2) Удельное объемное сопротивление — электрическое сопротивление диэлектрика постоянному току. Чем больше удельное сопротивление диэлектрика, тем меньше утечка накопленных зарядов в конденсаторе.

КОНДЕНСАТОР В ЦЕПИ ПОСТОЯННОГО ТОКА.

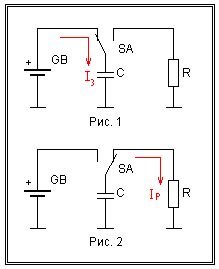Если подключить конденсатор к источнику электрической энергии GB, то в момент включения через конденсатор потечет ток Iз зарядки конденсатора (рис. 1).
Как только конденсатор зарядится, ток в цепи станет равным 0. Если конденсатор отключить от источника GB, то заряд накопленный в конденсаторе сохраниться. Если конденсатор отключить от источника GB и подключить к резистору R (рис. 2), то через резистор потечет ток разряда конденсатора Iр. Заряд накопленный в конденсаторе расходуется на разогрев резистора и в конечном итоге конденсатор разрядится.

На графике накопление заряда конденсатором выглядит как показано на рисунке 1.

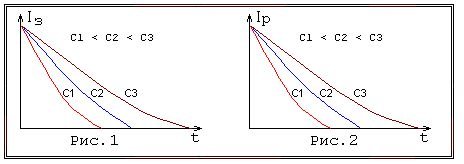
Время заряда конденсатора зависит от ёмкости конденсатора (при одинаковом приложенном напряжении). Чем больше ёмкость конденсатора, тем больше время заряда. Аналогичная картина (Рис. 2) наблюдается при разрядке конденсатора на сопротивление. При одинаковом сопротивлении время разряда больше у конденсатора с большей ёмкостью.

КОНДЕНСАТОР В ЦЕПИ ПЕРЕМЕННОГО ТОКА. Если напряжение приложенное к емкостному элементу, будет изменяться по амплитуде (переменное напряжение),то будет изменяться и заряд конденсатора, то есть в емкостном элементе появится ток.

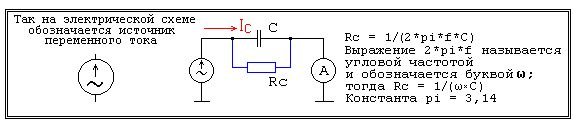
Ток Ic проходящий через конденсатор зависит от частоты f приложенного переменного напряжения и ёмкости С конденсатора. Если для постоянного тока сопротивление конденсатора можно считать равным бесконечности, то для переменного тока конденсатор обладает определённым сопротивлением. Сопротивление конденсатора переменному току Rc рассчитывается по формуле показанной на рисунке.
В формуле расчета емкостного сопротивления переменному току частота выражается в герцах, а емкость конденсатора в фарадах. Из формулы видно, что с увеличением частоты f при неизменной емкости конденсатора сопротивление Rc снижается, аналогично с увеличением емкости конденсатора при неизменной частоте сопротивление Rc так же снижается. Конденсаторы, так же как и резисторы, для получения заданной емкости Со можно включать параллельно и последовательно. Формулы расчета результирующей емкости показаны на рисунке.

КОНСТРУКЦИЯ, ПАРАМЕТРЫ И ТИПЫ КОНДЕНСАТОРОВ. Предположим, что мы конструируем конденсатор и попробуем, уже обладая определенными знаниями, рассчитать емкость конденсатора. Как известно, емкость конденсатора зависит от площади обкладок S, расстояния между обкладками d и диэлектрической проницаемости применяемого диэлектрика Er. Обкладки конденсатора изготавливаются из металлов с хорошей электрической проводимостью — алюминий, медь, серебро, золото. Емкость конденсатора не зависит от толщины обкладок, поэтому чем тоньше обкладки конденсатора, тем лучше — экономим металл и уменьшаем геометрический объём конденсатора.

Расстояние d не должно быть слишком малым, во избежание электрического пробоя диэлектрика.
Выберем в качестве диэлектрика наиболее распространенный материал — гетинакс с Er равной 6 . 8. Примем Er для нашего конденсатора равной 7.

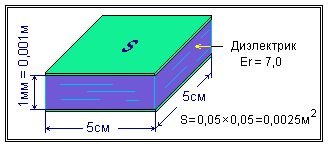
Площадь S вычисляется для одной обкладки конденсатора при условии, что линейные размеры обкладок одинаковы. Если одна из обкладок имеет меньшие длину или ширину то площадь вычисляется для меньшей обкладки.
Все размеры — длина и ширина обкладок и расстояние между ними должны быть выражены в метрах. Примем размеры такие, какие показаны на рисунке. Подставим в формулу расчета емкости конденсатора наши данные: C = Er * Eo * S / d;
C = 7 * 8.854*10 -12 * 0.0025 / 0.001= 0.000000000155Ф (фарады).
Возведем полученный результат в 12 степень чтобы получить значение емкости в пикофарадах:
C = 0.000000000155 12 = 155пФ.
Полученная нами ёмкость конденсатора 155пф очень мала, обычно такие ёмкости используются в аппаратуре работающей на высоких частотах переменного тока порядка 1 — 600 МГц (мегагерц).
Представьте себе, что мы разрабатываем миниатюрный карманный радиоприемник в котором требуется порядка 30 таких конденсаторов.

Если мы установим в схему 30 разработанных нами конденсаторов, не считая других необходимых радиодеталей, то наш радиоприемник никак не получится миниатюрным. Все дело в том, что объём только наших конденсаторов получится таким, что его никак нельзя будет назвать приемлемым.
Объем одного конденсатора Vc равен Vc = 5см * 5см * 0,1см
Vc = 2,5см в кубе. Тогда объем 30 конденсаторов будет равен:
V = 30 * 2,5 = 75см в кубе.
Что делать, как быть, как уменьшить геометрический объем конденсатора для применения в миниатюрной радиоаппаратуре? Для решения этой проблемы максимально уменьшают расстояние между обкладками, тогда увеличивается емкость и уменьшается геометрический объем конденсатора. Но расстояние уменьшают до определенных пределов иначе конденсатор будет пробиваться даже при низком напряжении подаваемом на конденсатор. В связи с этим на каждом конденсаторе указывается напряжение которое он может выдержать.

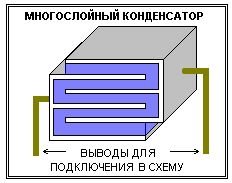
Для уменьшения площади обкладок конденсатор делают многослойным состоящим как бы из нескольких параллельно включенных конденсаторов (вспомните формулу параллельного включения конденсаторов).
В качестве диэлектрика в миниатюрных конденсаторах используют тонкие пленки из синтетических материалов, а в качестве обкладок металлическую фольгу, чаще всего из алюминия.

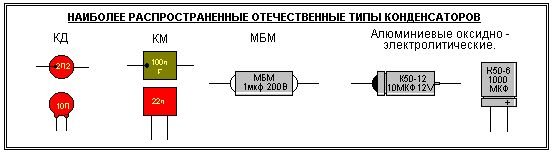
На корпусе конденсатора, обычно, указывается его тип, емкость и рабочее напряжение. Остальные параметры конденсатора определяются из справочников. Емкость конденсатора указывается не так, как на электрических схемах. Например емкость 2,2пФ обозначается 2П2, емкость 1500 пФ — 1Н5, емкость 0,1 мкФ — М1, емкость 2,2 мкФ — 2М2, емкость 10 мкФ — 10М.
У обычных конденсаторов КМ, КД, МБМ и так далее трудно получить большую ёмкость при малых габаритах поэтому были разработаны так называемые электролитические конденсаторы у которых в качестве диэлектрика используется специальная электролитическая жидкость с очень большим Er. Ёмкость таких конденсаторов может достигать сотен тысяч микрофарад. К недостатку таких конденсаторов следует отнести низкое рабочее напряжение (до 500V) и обязательное соблюдение полярности при включении в схему.
Для настройки и подстройки некоторых типов радиоаппаратуры, например радиоприемник или телевизор, применяют специальные конденсаторы с изменяемой ёмкостью.