Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие разным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно заранее учитывать при проектировании цепей.
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
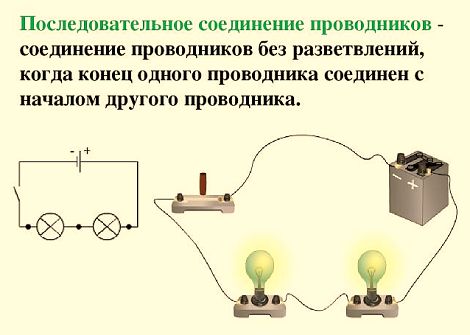
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Последовательное и параллельное соединение проводников. Практическая часть. 8 класс.
Ремонт светодиодных ламп
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
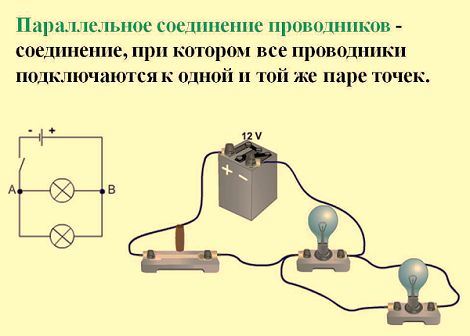
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
Диммер своими руками: устройство, принцип работы + как сделать диммер самому
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 – сопротивления обеих лампочек, U = U1 = U2 – значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях – увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Последовательное соединение
На рисунке показано последовательное соединение, в которое включены три лампочки и источник тока.
Если такое соединение подключают к источнику тока, тогда через все потребители течёт ток одинаковой силы .
I = I 1 = I 2 = I 3 = .
При последовательном соединении электрическое напряжение между полюсами источника тока постепенно распределяется на все последовательно включённые потребители. Напряжение на каждом участке можно рассчитать по закону Ома: (U = IR). Напряжение, которое таким образом рассчитано для участка цепи, называют падением напряжения .
U = U 1 + U 2 + U 3 + .
Общее сопротивление при последовательном соединении является суммой всех отдельных сопротивлений.
R = R 1 + R 2 + R 3 + .
Недостаток последовательного соединения такой: если на одном из участков цепи какой-либо из потребителей не работает (например, перегорела одна лампочка), тогда ток не течёт во всей цепи. Примером последовательного соединения является гирлянда новогодних лампочек.
Чем больше проводников включены в цепь последовательного соединения, тем будет больше общее сопротивление цепи и, вместе с тем, — меньше сила протекающего в цепи тока.
Рис. (2). Проводники
Источники тока выгодно связывать последовательным соединением (соединяя противоположные полюса), так как при этом общее напряжение цепи становится больше.
Рис. (3). Несколько источников тока
Последовательно с потребителем в цепь включают электрический предохранитель . Предохранитель размыкает электрическую цепь, если сила тока превышает допустимое значение.
Последовательное соединение потребителей
Последовательным соединением участков электрической цепи называют соединение, при котором через все участки проходит один и ток (рис.3.5).
Напряжение на каждом последовательно включенном участке пропорционально величине сопротивления этого участка.
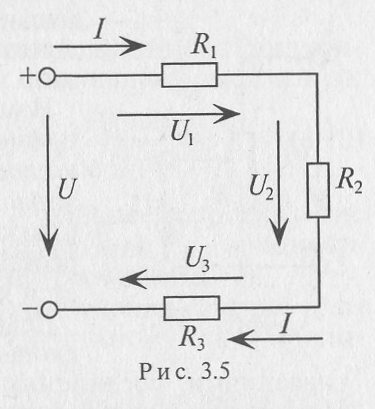
При последовательном соединении потребителей с сопротивлениями R1, R2 и R3 (рис. 3.5) напряжение на их зажимах равно
Воспользовавшись вторым законом Кирхгофа для рассматриваемой цепи (рис. 3.5), можно записать
Таким образом, общее (эквивалентное) сопротивление R последовательно включенных сопротивлений (потребителей) равно сумме этих сопротивлений.
Ток в цепи последовательно включенных потребителей (рис. 3.5) определяется выражением
Нетрудно понять, что при изменении сопротивления хотя бы одного потребителя изменяется ток цепи, а следовательно, и режим работы (напряжение) всех последовательно включенных потребителей.
Поэтому последовательное соединение сопротивлений не нашло широкого практического применения.
Следует заметить, что при последовательном соединении резисторов на большем сопротивлении тратится большая мощность
Параллельное соединение потребителей
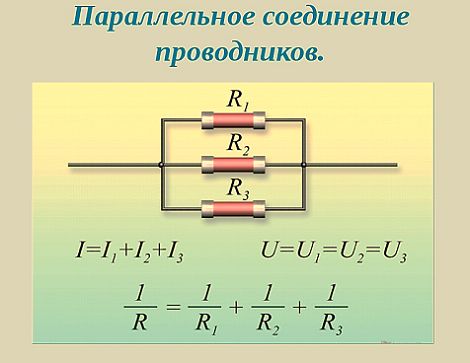
Параллельным соединением участков электрической цепи называют соединение, при котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под действием одного и того же напряжения (рис. 3.8). Токи параллельно включенных участков обратно пропорциональны сопротивлениям этих участков.
При параллельном соединении сопротивлений R1, R2 и R3 токи потребителей соответственно равны

Воспользовавшись первым законом Кирхгофа, можно определить ток I в неразветвленной части цепи
Таким образом, обратная величина общего (эквивалентного) сопротивления R параллельно включенных потребителей равна сумме обратных величин сопротивлений этих потребителей.
Величина, обратная сопротивлению, определяет проводимость потребителя g. Тогда общая (эквивалентная) проводимость цепи при параллельном соединении потребителей определяется суммой проводимостей потребителей
Если параллельно включены n одинаковых потребителей с сопротивлением R / каждый, то эквивалентное сопротивление этих потребителей . Если параллельно включены два потребителя с сопротивлениями R1 и R2, то их общее (эквивалентное) сопротивление в соответствии с (1.30) равно
Если параллельно включены три потребителя с сопротивлениями R1, R2, R3, то общее их сопротивление (см. (1.30))
Изменение сопротивления какого-либо из параллельно соединенных потребителей не влияет на режим работы (напряжение) других потребителей, включая изменяемое. Поэтому параллельное единение нашло широкое практическое применение.
При параллельном соединении потребителей на большем сопротивлении тратится меньшая мощность:
При изучении и расчете некоторых электрических цепей необходимо определить потенциалы отдельных точек цепи и построить потенциальную диаграмму. Для этого можно использовать выражение (3.4) (рис. 3.1а).
На участке АВ точка В имеет положительный потенциал , точка А — отрицательный потенциал , поэтому , так как источник работает в режиме генератора, т. е.
На участке ВС точка В имеет положительный потенциал , точка С — отрицательный , поэтому , источник с ЭДС Е2 работает в режиме потребителя, т. е.
Таким образом, потенциал точки D можно записать
если обходить цепь по направлению тока, или
если обходить цепь против направления тока.
Отсюда можно сделать следующий вывод (правило): если обходить цепь или участок цепи по направлению тока, то потенциал в каждой точке определяется потенциалом предыдущей точки плюс ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя, и минус падение напряжения на участке между точками цепи.
При обходе контура против направления тока знаки ЭДС и падения напряжения изменяются на противоположные.
Это правило особенно удобно применять в тех случаях, когда в цепи имеются участки с несколькими источниками.
Потенциальная диаграмма представляет собой график зависимости потенциалов точек цепи от величины сопротивлений участков между этими точками.
Для построения потенциальной диаграммы одну из точек электрической цепи условно заземляют, (потенциал ее принимают равным нулю), а потенциалы остальных точек равны напряжению между ними и заземленной точкой.
Потенциальная диаграмма представляет собой ломаную линию (рис. 3.3).
Для цепи, изображенной на рис. 3.2, дано:
Е1 = 8 В; Е2 = 24В; Е3 = 9,5 В; R1 = 0,5 Ом; R2 = 1 Ом; R3 = 1,5 Ом; R01 = 0,15 Ом; R02 = 0,1 Ом; R03 = 0 Ом.
1. Определить величину и направление тока в цепи.
2. Определить потенциал точек В, С, D, Е, G, приняв потенциал точки А равным нулю, .
3. Построить потенциальную диаграмму.
4. Составить и проверить баланс мощностей для цепи.
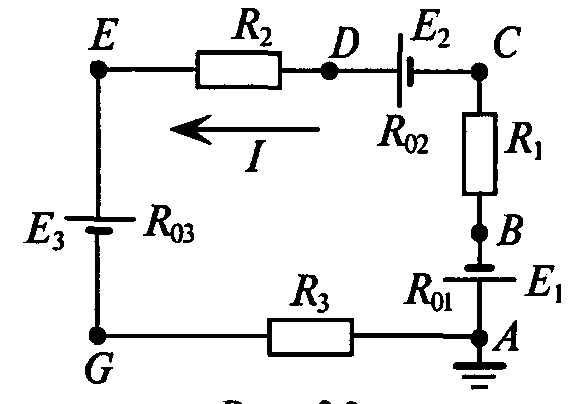
1. Выбираем направление обхода контура по часовой стрелке, тогда величина тока
Знак «минус», полученный в результате вычислений, указывает на то, что ток направлен против выбранного направления обхода, как показано на рис. 3.2. В дальнейших расчетах знак «минус» не учитывается. Таким образом, источник ЭДС Е2 работает в режиме генератора, а Е1 и Е3 — потребителей.
2. Для определения потенциалов указанных точек обходим контур по направлению тока. При этом получаем
3. Для построения потенциальной диаграммы по оси ординат в масштабе откладываются потенциалы точек, а по оси абсцисс — сопротивления участков. Потенциальная диаграмма изображена на рис. 3.3.
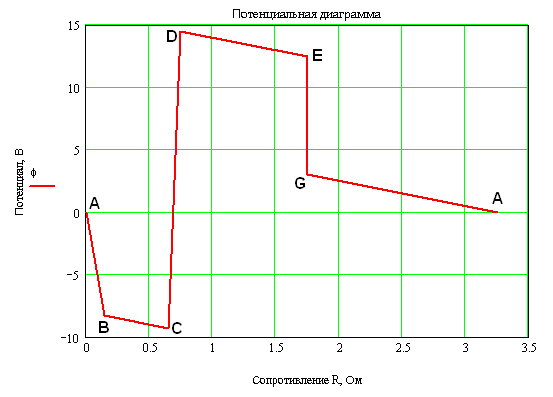
4. Баланс мощностей в электрической цепи с несколькими источниками соблюдается при условии, что сумма мощностей источников, работающих в режиме генераторов, равна сумме мощностей источников, работающих в режиме потребителей, и потерям мощностей на всех сопротивлениях цепи, включая внутренние сопротивления источников:
Рассчитать и построить потенциальную диаграмму для электрической цепи постоянного тока (рис. 1.19, а), если дано: ЭДС источников питания Е1 = 16 В; Е2 = 14 В, внутреннее сопротивление R01 = 3 Ом; R02 = 2 Ом, сопротивления резисторов R1 = 20 Ом; R2 = 15 Ом; R3 = 10 Ом. Определить положение движка потенциометра, в котором вольтметр V покажет нуль, составить баланс мощностей для цепи. Как повлияет на вид потенциальной диаграммы выбор другой точки с нулевым потенциалом?
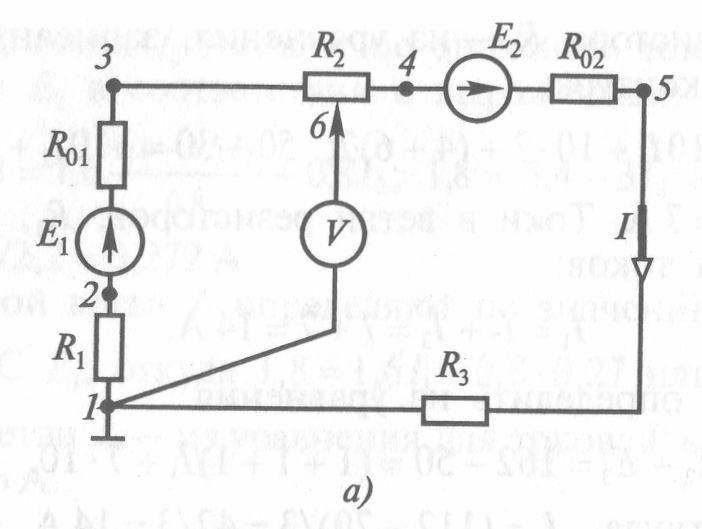
Решение. Ток в цепи определяют по уравнению, составленному по второму закону Кирхгофа, приведенному к виду:
Потенциальную диаграмму строят в прямоугольной системе координат. При этом по оси абсцисс откладывают в соответствующем масштабе сопротивления всех участков цепи, а по оси ординат — потенциалы соответствующих точек. При построении потенциальной диаграммы одна из точек цепи условно заземляется, т. е. принимается, что потенциал ее φ = 0. На диаграмме эта точка помещается в начале координат.
В соответствии с условием задачи определяют потенциалы точек 1 — 5 электрической цепи, при этом принимают потенциал φ1 точки 1 цепи равным нулю.
Потенциал φ2 точки 2 находят из выражения, записанного по второму закону Кирхгофа для участка 1 — 2 цепи:
Координаты точки 2: R = 20 Ом; φ2 = -12 В.
По второму закону Кирхгофа для участка цепи 1 — 3 справедливо уравнение:
откуда потенциал точки 3 цепи: .
Координаты точки 3 цепи: R = 20 + 3 = 23 Ом; φ3 = 2,2 В. Аналогично определяют потенциал точки 4 цепи:
Координаты точки 4 цепи: R = 23 + 15 = 38 Ом; φ4 = — 6,8В.
Потенциал φ5 точки 5 цепи находят из уравнения, записанного по второму закону Кирхгофа для участка 4 — 5 цепи:
Координаты точки 5 цепи: R = 38 + 2 = 40 Ом; φ5 = 6 В. Потенциал φ1 точки 1 цепи находят из уравнения, составленного по второму закону Кирхгофа для участка 4 — 5 цепи: ; . Координаты точки 1 цепи: R = 40 + 10 = 50 Ом; φ1 = 0.
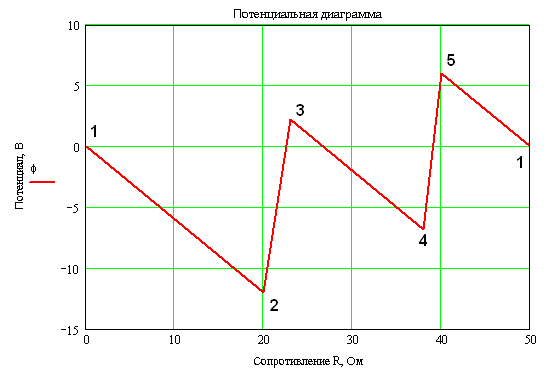
Для рассматриваемой электрической цепи по результатам расчетов на рис. 1.19, б приведена потенциальная диаграмма.
Из этой диаграммы следует, что положение движка потенциометра в точке 6 цепи соответствует показанию вольтметра, равному нулю, так как потенциалы точек 1 и 6 цепи равны.
При выборе другой точки электрической цепи с нулевым потенциалом разности потенциалов на соответствующих участках цепи не изменяются, так как они определяются величиной тока и величиной сопротивления. Если принять потенциал точки 3 цепи φ3 = 0, то ось абсцисс переместится в точку 3 потенциальной диаграммы (пунктирная линия), т. е. потенциалы всех точек цепи уменьшаются на величину потенциала φ, равного отрезку 0К = 2,3 В.
Баланс мощностей соответствует следующему уравнению:
16 ∙ 0,6 + 14 ∙ 0,6 = 0,6 2 (20 + 3 + 15 + 2 + 10).
Составить схему электрической цепи постоянного тока исходя из данных потенциальной диаграммы, приведенной на рис. 1.20,а.
Решение. Построение электрической цепи целесообразно начать с точки 1, которая совпадает с началом координат и, следовательно, имеет потенциал φ = 0 (точка заземлена).
Так как на потенциальной диаграмме сопротивления отдельных участков цепи откладываются в определенном масштабе по оси абсцисс, а по оси ординат — потенциалы, то каждой точке цепи соответствует точка на потенциальной диаграмме.
Из приведенной потенциальной диаграммы следует, что при переходе от точки 1 к точке 2 цепи потенциал линейно возрастает. При этом тангенс угла α1 наклона прямой 0 — 2 к оси абсцисс пропорционален потенциалу точки 2. Следовательно, согласно диаграмме, на участке цепи 1 — 2 должен быть включен резистор с сопротивлением R1 = 2 Ом.
Так как при переходе от точки 1 к точке 2 цепи потенциал увеличивается, то ток цепи направлен от точки 2 к точке 1 цепи:
На участке 2 — 3 диаграммы потенциал растет скачком. Это свидетельствует о том, что между соответствующими точками цепи включен источник ЭДС, направление которой встречно току (источник работает в режиме потребителя электроэнергии).
Согласно потенциальной диаграмме ЭДС, Е23 = 40 В.
На участке 3 — 4 цепи, согласно диаграмме, должен быть включен резистор, имеющий сопротивление R2 = 1 Ом. На этом участке . При этом .
На участке 4 — 5 цепи, согласно диаграмме, должен быть включен источник ЭДС Е45 =75 В. Так как при переходе от точки 4 к точке 5 цепи потенциал понижается, то ЭДС должна быть направлена от точки 5 к точке 4 цепи.
На участке 5 — 6 цепи потенциал повышается на величину , поэтому здесь должен быть включен резистор с сопротивлением R3 = 1 Ом.
На участке 6 — 7 цепи потенциал резко возрастает. Здесь, согласно диаграмме, должен быть включен источник ЭДС Е67 = 45 В, который работает в схеме в режиме потребителя.
При переходе от точки 7 к точке 8 цепи потенциал возрастает на величину, равную произведению , так как здесь должен быть включен резистор с сопротивлением R4 = 3 Ом.
На участке 8 — 9 цепи потенциал уменьшается скачком вследствие того, что источник ЭДС Е89 = 55 В подключен положительным полюсом к точке 8, а отрицательным — к точке 9. В данном случае источник ЭДС Е89 работает в цепи в качестве источника питания.
На участке 9 — 1 цепи потенциал повышается на величину, равную произведению . Поэтому здесь должен быть включен резистор с сопротивлением R5 = 2 Ом.
Результаты определения потенциалов рассматриваемой электрической цепи приведены в табл. 1.2.
Участок электрической цепи
Сопротивление участка, Ом
Напряжение в цепи при последовательном соединении проводников
Используя закон Ома для участка цепи, мы можем найти напряжение и на концах этих участков:
$U_1 = IR_1$,
$U_2 = IR_2$,
…
$U_n = IR_n$.
Получается, что напряжение будет тем больше, чем больше сопротивление на участках цепи. Сила тока же везде будет одинакова.
Как найти напряжение участка цепи, состоящего из последовательно соединенных проводников, зная напряжение на каждом?
Полное напряжение в цепи при последовательном соединении, или напряжение на полюсах источника тока, равно сумме напряжений на отдельных участках цепи:
$U = U_1 + U_2 + … + U_n$.
Полное напряжение в цепи и закон сохранения энергии
Давайте вспомним, что напряжение определяется работой электрического тока. Эта работа совершается при прохождении по участку цепи электрического заряда, равного $1 space Кл$:
$U = frac$.
За счет чего совершается эта работа? Мы уже говорили, что электрическое поле обладает некоторой энергией. Именно за счет нее и идет совершение работы.
Такая работа совершается на каждом участке цепи, которую мы рассматриваем. Пользуясь законом сохранения энергии, мы можем сделать следующий вывод.
Энергия, израсходованная на всей цепи, равна сумме энергий, которые расходуются на отдельных ее участках (проводниках).
Последовательное соединение проводников
Сопротивление при последовательном соединении проводников
Последовательное соединение проводников — это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

Пример
У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.
Решение
То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор RAB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:
Сила тока через последовательное соединение проводников
Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор RAB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R1 , R2 , R3 , то получится, что через них течет та же самая сила тока, которая текла через резистор RAB .

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R1 течет такая же сила тока, как и через резистор R2 и такая же сила тока течет через резистор R3 .
Напряжение при последовательном соединении проводников
Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?
Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на любом резисторе. Давайте так и сделаем.
Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае RAB =R1 + R2 + R3 = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.
Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения UR1 , UR2 , UR3 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.
Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.
Мы получили самый простой делитель напряжения.
Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.
Параллельное соединение проводников
Параллельное соединение проводников выглядит вот так.

Ну что, думаю, начнем с сопротивления.
Сопротивление при параллельном соединении проводников
Давайте пометим клеммы как А и В
В этом случае общее сопротивление RAB будет находиться по формуле

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников
Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.
Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников
Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.
Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что
Если бы у нас еще были резисторы, соединенные параллельно, то для них
В этом случае, сила тока в цепи будет равна:

Задача
Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение
Воспользуемся формулами, которые приводили выше.
Если бы у нас еще были резисторы, соединенные параллельно, то для них
Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи
2-ой способ найти I
Чтобы найти Rобщее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них — «калькулятор резисторов«. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть Rобщее = 1,25 Ом.
I=U/Rобщее = 10/1,25=8 Ампер.
Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.
Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.
Подробное объяснение на видео:
Прикольный набор радиолюбителя по ссылке
Похожие статьи по теме «последовательное и параллельное соединение»
Закономерности последовательного и параллельного соединения проводников
Электрическая цепь представляет собой совокупность проводников и источников тока. При этом на отдельных участках цепи проводники могут соединяться последовательно или параллельно.
При последовательном соединении проводники (резисторы) соединяются друг за другом. Здесь отсутствуют какие-либо разветвления проводников, а это значит, что через каждый проводник будет протекать один и тот же ток. Общее напряжение будет складываться из напряжений на каждом проводнике. Имея в наличии три резистора, соединенных последовательно, можно утверждать, что их общее сопротивление равно сумме сопротивлений каждого из резисторов.
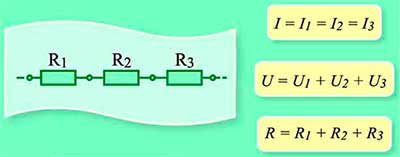
При параллельном соединении проводников начала и концы их соединяются вместе. В результате в точке разветвления проводников ток делится. Соответственно, общий ток будет складываться из токов, текущих через каждый проводник, а напряжение на каждом из них станет одинаковым. При параллельном соединении складываются величины, обратные сопротивлению проводников. В итоге получаем величину, обратную общему сопротивлению.
Основные законы
Проектирование электрических цепей предполагает наличие хороших знаний основных закономерностей последовательного и параллельного подключения нагрузки. Это касается не только закона Ома, но и постулатов Кирхгофа. Эти физики внесли большой вклад в развитие электротехники. Для более простого восприятия основных законов все формулы стоит рассматривать в следующей последовательности:
- при последовательном соединении через каждый участок цепи протекает ток одинаковой силы;
- общее сопротивление схемы при последовательном подключении равно сумме сопротивления всех проводников;
- напряжение в электросети при параллельном подключении одинаково для каждого участка;
В соответствии с первым законом Кирхгофа, алгебраическая сумма токов в узле всегда равна нулю. Благодаря этому, можно получить формулу для нахождения эквивалентного сопротивления цепи, если известно сопротивление каждой нагрузки. Она имеет следующий вид: Ro =R1*R2 / R1+R2.
Для последовательного соединения нагрузок применим второй закон Кирхгофа. Согласно ему, сумма ЭДС в замкнутом электрическом контуре равна сумме падений напряжений на каждой нагрузке. В результате общее сопротивление можно определить с помощью следующей формулы: Ro = R1 + R2.
Также можно рассчитать и индуктивность при различных видах соединения катушек. В случае с последовательным все довольно просто, достаточно использовать следующую формулу: Lo = L1 + L2. По сути, вместо двух элементов можно установить один с соответствующим показателем индуктивности.
При параллельном подсоединении катушек ситуация усложняется, так как возможны три варианта:
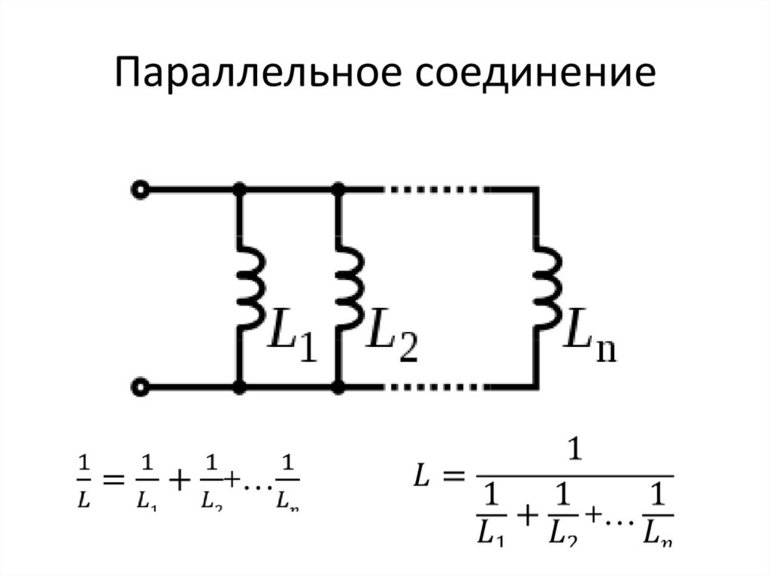
- магнитные поля катушек не пересекаются: Lo = L1 * L2 / L1 + L2;
- катушки подсоединены в одном направлении и их поля пересекаются: Lo = L1 * L2-М 2 / L1 + L2 — 2 М;
- пересечение полей наблюдается при встречном подсоединении: Lo = L1 * L2-М 2 / L1 + L2 + 2 М.
Сегодня часто для расчета этих и других показателей, например, емкости конденсатора, можно использовать онлайн-калькулятор.
Особенности применения
Каждый из методов подключения нагрузки нашел свое применение в быту и промышленности. Параллельный способ целесообразно использовать в ситуации, когда электроприбор требуется целенаправленно отключать. Примером здесь может стать электрический звонок, соединенный последовательно с источником питания и кнопкой. В соответствии с этим же принципом работает и ручной фонарик, состоящий из светодиода, ключа и батарейки.

Однако последовательное включение приборов не всегда позволяет решить поставленные задачи. В каждой квартире присутствует большое количество осветительных приборов. Если все их соединить последовательно, то они будут включаться и отключаться одновременно, что требуется крайне редко. Именно люстры принято подключать параллельно. В результате у потребителя появится возможность активировать нужное в данный момент количество ламп. Благодаря этому, достигается требуемая освещенность помещения и экономится электрическая энергия.
В быту чаще всего используется смешенное подключение нагрузок. Этот вид подсоединения проводников является сочетанием параллельного и последовательного соединения. При этом на стадии проектирования электросети крайне важно учитывать все преимущества и недостатки каждого типа подсоединения. Для определения необходимых показателей общую цепь следует разделить на простые участки, а полученные результаты затем суммируются.




