На прошлых уроках мы уже упоминали о том, что электрическое поле обладает некоторой энергией. Значит, оно способно совершить какую-то работу. Эту работу называют работой электрического тока.
А теперь вспомним уже известное нам определение механической работы. Она определяется силой, действующей на тело, и расстоянием, на которое это тело перемещается: $A = Fs$.
Если мы перенесем эти знания на электрические явления, то сможем сказать, что работа тока — это работа электрических сил, которые перемещают заряженные частицы в проводнике. Но если мы будем использовать формулу $A = Fs$ для каждой частицы, то последующие расчеты будут невероятно сложными. Ведь тогда нам нужно будет знать и точное количество заряженных частиц, и точное расстояние, которое они прошли под действием сил электрического поля.
Мы пойдем другим путем. Он будет гораздо проще и понятнее. На данном уроке мы дадим определение работы электрического тока через другие электрические величины (силу тока, напряжение, электрический заряд). Также мы научимся рассчитывать работу электрического тока, используя полученные знания.
Работа электрического тока и напряжение
Чему равно электрическое напряжение на участке цепи?
Вспомним определение этой величины. Мы говорили, что напряжение на концах проводника (участка цепи) равно работе, которая совершается при прохождении по этому проводнику заряда, равному $1 space Кл$: $U = frac$.
Как через напряжение и электрический заряд, прошедший через участок цепи, выразить работу электрического тока на этом участке?
Используя формулу электрического напряжения, выразим работу электрического тока.
$A = Uq$.
Чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд (количество электричества), прошедший по нему.
Какая мощность определяет полезную работу совершаемую эц
При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δ по цепи протекает заряд Δ = Δ. Электрическое поле на выделенном учестке совершает работу
| Δ = (φ1 – φ2) Δ = Δφ12 Δ = Δ, |
где = Δφ12 – напряжение. Эту работу называют работой электрического тока .
Если обе части формулы
выражающей закон Ома для однородного участка цепи с сопротивлением , умножить на Δ, то получится соотношение
Это соотношение выражает закон сохранения энергии для однородного участка цепи.
Работа Δ электрического тока , протекающего по неподвижному проводнику с сопротивлением , преобразуется в тепло Δ, выделяющееся на проводнике.
Мощность
Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца .
Мощность электрического тока равна отношению работы тока Δ к интервалу времени Δ, за которое эта работа была совершена:
Работа электрического тока в СИ выражается в джоулях (Дж), мощность – в ваттах (Вт).
Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением и внешнего однородного участка с сопротивлением . Закон Ома для полной цепи записывается в виде
Умножив обе части этой формулы на Δ = Δ, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:
| 2 Δ + 2 Δ = Δ = Δст. |
Первый член в левой части Δ = 2 Δ – тепло, выделяющееся на внешнем участке цепи за время Δ, второй член Δист = 2 Δ – тепло, выделяющееся внутри источника за то же время.
Выражение Δ равно работе сторонних сил Δст, действующих внутри источника.
При протекании электрического тока по замкнутой цепи работа сторонних сил Δст преобразуется в тепло, выделяющееся во внешней цепи (Δ) и внутри источника (Δист) .
| Δ + Δист = Δст = Δ |
Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами , действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.
Внешняя цепь может представлять собой не только проводник с сопротивлением , но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под нужно понимать эквивалентное сопротивление нагрузки . Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, но и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.
Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна
Во внешней цепи выделяется мощность
Отношение равное
называется коэффициентом полезного действия источника .
На рис. 1.11.1 графически представлены зависимости мощности источника ист, полезной мощности , выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи для источника с ЭДС, равной , и внутренним сопротивлением . Ток в цепи может изменяться в пределах от = 0 (при ) до (при = 0).
Зависимость мощности источника ист, мощности во внешней цепи и КПД источника η от силы тока
Из приведенных графиков видно, что максимальная мощность во внешней цепи max, равная
достигается при = . При этом ток в цепи
а КПД источника равен 50 %. Максимальное значение КПД источника достигается при , т. е. при . В случае короткого замыкания полезная мощность = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль.
Мощность и коэффициент полезного действия
Мощность по своей сути является скоростью выполнения работы. Чем больше мощность совершаемой работы, тем больше работы выполняется за единицу времени.
Среднее значение мощности — это работа, выполненная за единицу времени.
Величина мощности прямо пропорциональна величине совершённой работы (A) и обратно пропорциональна времени (t), за которое работа была совершена.
Мощность (N) определяют по формуле:
Единицей измерения мощности в системе (СИ) является (Ватт) (русское обозначение — (Вт), международное — (W)).
Для определения мощности двигателя автомобилей и других транспортных средств используют исторически более древнюю единицу измерения — лошадиная сила (л.с.), 1 л.с. = 736 Вт.
Мощность двигателя автомобиля равна примерно (90 л.с. = 66240 Вт).
Мощность автомобиля или другого транспортного средства можно рассчитать, если известна сила тяги автомобиля (F) и скорость его движения (v).
Эту формулу получают, преобразуя основную формулу определения мощности.
Ни одно устройство не способно использовать (100) % от начально подведённой к нему энергии на совершение полезной работы. Поэтому важной характеристикой любого устройства является не только мощность, но и коэффициент полезного действия, который показывает, насколько эффективно используется энергия, подведённая к устройству.
Для того чтобы автомобиль двигался, должны вращаться колёса. А для того чтобы вращались колёса, двигатель должен приводить в движение кривошипно-шатунный механизм (механизм, который возвратно-поступательное движение поршня двигателя преобразует во вращательное движение колёс). При этом приводятся во вращение шестерни и большая часть энергии выделяется в виде тепла в окружающее пространство, в результате чего происходит потеря подводимой энергии. Коэффициент полезного действия двигателя автомобиля находится в пределах (40 — 45) %. Таким образом, получается, что только около (40) % от всего бензина, которым заправляют автомобиль, идёт на совершение необходимой нам полезной работы — перемещение автомобиля.
Если мы заправим в бак автомобиля (20) литров бензина, тогда только (8) литров будут расходоваться на перемещение автомобиля, а (12) литров сгорят без совершения полезной работы.
Коэффициент полезного действия обозначается буквой греческого алфавита («эта») η , он является отношением полезной мощности (N) к полной или общей мощности N полная .
Для его определения используют формулу: η = N N полная . Поскольку по определению коэффициент полезного действия является отношением мощностей, единицы измерения он не имеет.
Часто его выражают в процентах. Если коэффициент полезного действия выражают в процентах, тогда используют формулу: η = N N полная ⋅ 100 % .
Так как мощность является работой, проделанной за единицу времени, тогда коэффициент полезного действия можно выразить как отношение полезной проделанной работы (A) к общей или полной проделанной работе A полная . В этом случае формула для определения коэффициента полезного действия будет выглядеть так:
Работа и мощность электрического тока. Закон Джоуля-Ленца
1. Электрический ток, проходя по цепи, производит разные действия: тепловое, механическое, химическое, магнитное. При этом электрическое поле совершает работу, и электрическая энергия превращается в другие виды энергии: во внутреннюю, механическую, энергию магнитного поля и пр.
Как было показано, напряжение ( (U) ) на участке цепи равно отношению работы ( (F) ) , совершаемой при перемещении электрического заряда ( (q) ) на этом участке, к заряду: ( U=A/q ) . Отсюда ( A=qU ) . Поскольку заряд равен произведению силы тока ( (I) ) и времени ( (t) ) ( q=It ) , то ( A=IUt ) , т.е. работа электрического тока на участке цепи равна произведению напряжения на этом участке, силы тока и времени, в течение которого совершается работа.
Единицей работы является джоуль (1 Дж). Эту единицу можно выразить через электрические единицы:
( [A] ) = 1 Дж = 1 В · 1 А · 1 с
Для измерения работы используют три измерительных прибора: амперметр, вольтметр и часы, однако, в реальной жизни для измерения работы электрического тока используют счётчики электрической энергии.
Если нужно найти работу тока, но при этом сила тока или напряжение неизвестны, то можно воспользоваться законом Ома, выразить неизвестные величины и рассчитать работу по формулам: ( A=fract ) или ( A=I^2Rt ) .
2. Мощность электрического тока равна отношению работы ко времени, за которое она совершена: ( P=A/t ) или ( P=IUt/t ) ; ( P=IU ) , т.е. мощность электрического тока равна произведению напряжения и силы тока в цепи.
Единицей мощности является ватт (1 Вт): ( [P]=[I]cdot[U] ) ; ( [P] ) = 1 А · 1 В = 1 Вт.
Используя закон Ома, можно получить другие формулы для расчета мощности тока: ( P=frac;P=I^2R ) .
Значение мощности электрического тока в проводнике можно определить с помощью амперметра и вольтметра, измерив соответственно силу тока и напряжение. Можно для измерения мощности использовать специальный прибор, называемый ваттметром, в котором объединены амперметр и вольтметр.
3. При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: ( Q=A ) или ( Q=IUt ) . Учитывая, что ( U=IR ) , ( Q=I^2Rt ) .
Количество теплоты, выделяющееся при прохождении тока но проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени.
Этот закон называют законом Джоуля-Ленца.
ПРИМЕРЫ ЗАДАНИЙ
1. Силу тока в проводнике увеличили в 2 раза. Как изменится количество теплоты, выделяющееся в нём за единицу времени, при неизменном сопротивлении проводника?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
2. Длину спирали электроплитки уменьшили в 2 раза. Как изменится количество теплоты, выделяющееся в спирали за единицу времени, при неизменном напряжении сети?
1) увеличится в 4 раза
2) уменьшится в 2 раза
3) увеличится в 2 раза
4) уменьшится в 4 раза
3. Сопротивления резистор ( R_1 ) в четыре раза меньше сопротивления резистора ( R_2 ) . Работа тока в резисторе 2

1) в 4 раза больше, чем в резисторе 1
2) в 16 раз больше, чем в резисторе 1
3) в 4 раза меньше, чем в резисторе 1
4) в 16 раз меньше, чем в резисторе 1
4. Сопротивление резистора ( R_1 ) в 3 раза больше сопротивления резистора ( R_2 ) . Количество теплоты, которое выделится в резисторе 1
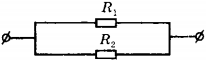
1) в 3 раза больше, чем в резисторе 2
2) в 9 раз больше, чем в резисторе 2
3) в 3 раза меньше, чем в резисторе 2
4) в 9 раз меньше, чем в резисторе 2
5. Цепь собрана из источника тока, лампочки и тонкой железной проволоки, соединенных последовательно. Лампочка станет гореть ярче, если
1) проволоку заменить на более тонкую железную
2) уменьшить длину проволоки
3) поменять местами проволоку и лампочку
4) железную проволоку заменить на нихромовую
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения напряжения на концах двух проводников (1) и (2) одинакового сопротивления. Сравните значения работы тока ( A_1 ) и ( A_2 ) в этих проводниках за одно и то же время.
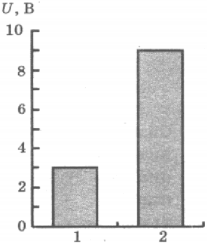
1) ( A_1=A_2 )
2) ( A_1=3A_2 )
3) ( 9A_1=A_2 )
4) ( 3A_1=A_2 )
7. На рисунке приведена столбчатая диаграмма. На ней представлены значения силы тока в двух проводниках (1) и (2) одинакового сопротивления. Сравните значения работы тока ( A_1 ) и ( A_2 ) в этих проводниках за одно и то же время.
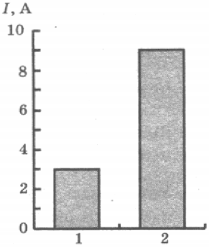
1) ( A_1=A_2 )
2) ( A_1=3A_2 )
3) ( 9A_1=A_2 )
4) ( 3A_1=A_2 )
8. Если в люстре для освещения помещения использовать лампы мощностью 60 и 100 Вт, то
А. Большая сила тока будет в лампе мощностью 100 Вт.
Б. Большее сопротивление имеет лампа мощностью 60 Вт.
Верным(-и) является(-ются) утверждение(-я)
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
9. Электрическая плитка, подключённая к источнику постоянного тока, за 120 с потребляет 108 кДж энергии. Чему равна сила тока в спирали плитки, если её сопротивление 25 Ом?
1) 36 А
2) 6 А
3) 2,16 А
4) 1,5 А
10. Электрическая плитка при силе тока 5 А потребляет 1000 кДж энергии. Чему равно время прохождения тока по спирали плитки, если её сопротивление 20 Ом?
1) 10000 с
2) 2000 с
3) 10 с
4) 2 с
11. Никелиновую спираль электроплитки заменили на нихромовую такой же длины и площади поперечного сечения. Установите соответствие между физическими величинами и их возможными изменениями при включении плитки в электрическую сеть. Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) электрическое сопротивление спирали
Б) сила электрического тока в спирали
B) мощность электрического тока, потребляемая плиткой
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличилась
2) уменьшилась
3) не изменилась
12. Установите соответствие между физическими величинами и формулами, по которым эти величины определяются. Запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) работа тока
Б) сила тока
B) мощность тока
Мощность источника питания
В предыдущем разделе было рассмотрено понятие мощности и относящиеся к ней характеристики в применении к различным электрическим узлам или приборам. При рассмотрении источника элетротока потребуется учитывать имеющиеся в этом случае особенности.
Используемый ИП должен соответствовать параметрам электрической цепи, которую он питает. При этом необходимо обратить внимание на следующее:
- Значение полной мощности электрической цепи.
- ЭДС источника.
- Внутренне сопротивление ИП.
- Потери энергии внутри источника питания.
- Значение полезной мощности.
Мощность источника тока должна превосходить мощность электроприбора не меньше, чем на 5-10%. Это позволит обеспечить электропитание даже в условиях интенсивного использования прибора. Энергия источника питания будет расходоваться на совершение полезной работы, а также на потери.
Для понимания особенностей работы источника питания важно знать разницу между электронапряжением на клеммах и электродвижущей силой. Практически в работающей цепи электроны перемещаются по замкнутому пути. Они переходят от отрицательной клеммы через электрическую цепь к положительной. Попадая внутрь батареи под воздействием электродвижущей силы, электроны будут вновь перемещаться на отрицательную клемму.

Нужно учитывать, что величина ЭДС не является независимой от нагрузки. Её точное значение можно узнать при измерении на холостом ходу. Чтобы вычислить мощность источника питания, можно воспользоваться формулой, которая выражает её через ЭДС и сопротивление. Для этого потребуется выполнить следующие действия:
- Нужно определить величину электродвижущей силы (E) источника питания. Для этого замеряют разность потенциалов на клеммах на холостом ходу.
- Далее требуется подключить нагрузку, которая имеет известное сопротивление (R).
- Затем в электрической цепи измеряют силу тока (I), а также напряжение (U).
- Теперь есть возможность узнать падение напряжения (U0) внутри источника тока. Оно представляет собой разность между электродвижущей силой и напряжением в цепи.
- Внутреннее сопротивление (R0) вычисляется по формуле R0 = U0 / I.
Подставив полученные значения в формулу, выраженную через напряжение и сопротивление, можно определить мощность источника тока.

Полную мощность ИП можно представить как Рполн = Рполезн + Рпотерь.
Для определения полезной мощности используется одна из трех формул:

Мощность потерь, возникающая во внутренней цепи, то есть, в источнике тока, расходуется лишь на процессы, происходящие в самом ИТ и не может использоваться для каких-либо других целей. Ее вычисляют по формуле:

Для определения полной мощности можно воспользоваться одной из трех формул:

Используя приведённый здесь алгоритм, можно определить полезную мощность, которая создаётся рассматриваемым источником тока. Чтобы составить представление о зависимости полезной мощности и той, которая расходуется на нагрев ИТ, можно воспользоваться графиком. Из него видно, что полезная мощность сначала возрастает, а затем начинает убывать. Максимума она достигает в точке, в которой сопротивление нагрузки равно внутреннему сопротивлению источника электротока, то есть, R = r.

КПД при таком условии будет равен 50%. В общем случае коэффициент полезного действия находят по формуле:

Максимальная полезная мощность равняется половине полной. Следовательно

Из сказанного видно, что при подборе наиболее подходящего источника питания для электрического устройства нужно стремиться к тому, чтобы внутреннее сопротивление источника питания было равно сопротивлению нагрузки. Если оно значительно меньше, то существенная часть мощности в процессе эксплуатации будет рассеиваться в виде тепла. Приведённое требование соответствия величин называют условием согласования.
Важно отметить, что в качестве устройства питания не обязательно может использоваться батарея или аккумулятор. Отмеченная здесь закономерность будет действовать и в том случае, если речь идёт об использовании усилителя.
В качестве примера использования указанного правила можно привести подключение акустической системы к усилителю. В этом случае выходной импеданс последнего должен подбираться таким образом, чтобы быть примерно равным входному импедансу подключённых динамиков. На практике в технической документации усилителя указывают границы, в которых должна находиться соответствующая характеристика подключённых устройств.
Полезная мощность: определение в физике




Мощностью в физике называется скорость выполнения работы: сколько затрачивается энергии (или выполняется работы) в единицу времени.
$P = frac implies P = F cdot v_$, где:
- $F$ — действующая сила,
- $S$ — пройденное расстояние,
- $t$ — затраченное время,
- $v_$ — средняя скорость.
Средняя мощность при вращении вычисляется аналогично:
- $F$ — сила,
- $r$ — радиус до точки приложения силы,
- $M$ — вращающий момент,
- $varphi$ — пройденное угловое расстояние,
- $omega_$ — средняя угловая скорость.
В электротехнике мощность постоянного тока вычисляется как произведение напряжения на его силу:
Мощность в системе СИ измеряется в ваттах. Ватт — количество джоулей, затрачиваемых в секунду.

Статья: Полезная мощность: определение в физике
Найди решение своей задачи среди 1 000 000 ответов
Говоря о полезной мощности, следует делать различие между работой и энергией. С физической точки зрения эти величины взаимозаменяемы, обе измеряются в джоулях. Однако под работой, как правило, подразумевается целенаправленный расход энергии, тогда как просто энергия может означать и явление, происходящее вне человеческих представлений о полезности. Например, при случайном взрыве резервуара с топливом выделяется огромное количество энергии, но называть такое явление работой было бы неправильно.
Соотношение полезной работы к расходу энергии называются коэффициентом полезного действия (КПД). Например, можно поднять груз на высоту 10 м с помощью электролебедки (часть электроэнергии при этом неизбежно преобразуется в ненужное тепло), а можно затащить на ту же высоту по наклонной плоскости (часть энергии будет затрачена на преодоление силы трения). Сопоставляя разные способы подъема груза, мы можем решить, какой из них менее затратен.
Замечание 1
Это рассуждение применимо и к мощности: полезная мощность определяется как та часть затрачиваемой ежесекундно энергии, которая расходуется на выполнение полезной работы, т.е. затрачиваемая в единицу времени энергия за вычетом затрат на преодоление сил трения, паразитных токов, вязкости окружающей среды и т.п.
Начинай год правильно
Выигрывай призы на сумму 400 000 ₽
Расчет средней полезной мощности при поступательном движении производится по формуле
$P = F cdot v_ cdot cos(alpha)$, где:
- $F$ — действующая сила,
- $S$ — пройденное расстояние,
- $alpha$ — угол между векторами скорости и силы,
- $v_$ — средняя скорость.
Чем меньше угол между векторами скорости и силы, тем большая часть мощности будет затрачиваться производительно, т.е. на выполнение полезной работы.
Какой мощности требуется лебедка для подъема груза весом 30 кг на высоту 5,5 м за 5,5 с? КПД лебедки принять равным 0,8.
Учитывая, что направления силы и скорости совпадают ($cos(alpha) = cos(0) = 1$), мощность можно найти как
Найдем вес груза (действующую на него силу тяжести), умножив массу на ускорение свободного падения:
$F = 9,8 cdot 20 approx 300 Н$.
Скорость как отношение перемещения к времени:
Мощность с учетом КПД:
$P = 0,8 cdot 300 cdot 1 approx 240 Вт $
Ответ: $approx 240 Вт$.
Коэффициент полезного действия
При выполнении необходимой (полезной) работы, например, механической, приходится выполнять работу большую по величине, так как в реальности существуют силы сопротивления и часть энергии подвержена диссипации (рассеиванию). Эффективность совершения работы определяется при помощи коэффициента полезного действия ($eta $), при этом:
где $P_p$ — полезная мощность; $P$ — затраченная мощность. Из выражения (5) следует, что полезная мощность может быть найдена как:
[P_p=eta P left(6right).]
Формула полезной мощности источника тока
Пусть электрическая цепь состоит из источника тока, имеющего сопротивление $r$ и нагрузки (сопротивление $R$). Мощность источника найдем как:
где $?$ — ЭДС источника тока; $I$ — сила тока. При этом $P$ — полная мощность цепи.
Обозначим $U$ — напряжение на внешнем участке цепи, тогда формулу (7) представим в виде:
где $P_p=UI=I^2R=frac(9)$ — полезная мощность; $P_0=I^2r$ — мощность потерь. При этом КПД источника определяют как:
Максимальную полезную мощность (мощность на нагрузке) электрический ток дает, если внешнее сопротивление цепи будет равно внутреннему сопротивлению источника тока. При этом условии полезная мощность равна 50% общей мощности.
При коротком замыкании (когда $Rto 0;;Uto 0$) или в режиме холостого хода $(Rto infty ;;Ito 0$) полезная мощность равна нулю.
Мощность тока
Любой электрический прибор (лампа, электродвигатель и пр.) рассчитан на потребление определенной энергии в единицу времени. Поэтому наряду с работой тока очень важное значение имеет понятие мощности тока.
Мощность тока — это работа, производимая за 1 секунду. Обозначается как P. Единица измерения — Ватт (Вт).
Численно мощность тока равна отношению работы тока за время ∆t к этому интервалу времени:
Это выражение для мощности можно переписать в нескольких эквивалентных формах, если использовать закон Ома для участка цепи:
P = I U = I 2 R = U 2 R . .
Пример №3. При силе тока в электрической цепи 0,3 А сопротивление лампы равно 10 Ом. Определите мощность электрического тока, выделяющуюся на нити лампы.
P = I 2 R = 0 , 3 2 · 10 = 0 , 9 ( В т )
Выразив силу тока через заряд, прошедший за единицу времени, получим:
Мощность тока равна мощности на внешней цепи. Ее также называют мощностью на нагрузке, полезной мощностью или тепловой мощностью. Ее можно выразить через ЭДС:
P = ( ε R + r . . ) 2 R
Мощность тока на внешней цепи будет максимальная, если сопротивление внешней цепи равно внутреннему сопротивлению: R = r.
P m a x = ( ε r + r . . ) 2 r = ε 2 4 r . .
Мощность тока внутренней цепи:
P в н у т р = I 2 r = ( ε R + r . . ) 2 r
P п о л н = I 2 ( R + r ) = ε 2 R + r . .
Пример №4. ЭДС постоянного тока ε = 2 В, а его внутреннее сопротивление r = 1 Ом. Мощность тока в резисторе, подключенном к источнику, P0 = 0,75 Вт. Чему равно минимальное значение силы тока в цепи?
Используем формулу для нахождения полезной мощности:
P = ( ε R + r . . ) 2 R
Применим закон Ома для полной цепи:
Выразим сопротивление внешней цепи:
P = ( ε ε I . . − r + r . . ) 2 ( ε I . . − r ) = I 2 ( ε I . . − r ) = I ε − r I 2
Так как внутреннее сопротивление равно единице, получаем квадратное уравнение следующего вида:
r I 2 − I ε + P = 0
I 2 − 1 I + 0 , 75 = 0
Решив это уравнение, получим два корня: I = 0,5 и I = 1,5 А. Следовательно, наименьшая сила тока равна 0,5 А.
Подсказки к задачам
Конденсатор в цепи постоянного тока
Постоянный ток через конденсатор не идет, но заряд на нем накапливается, и напряжение между обкладками поддерживается. Напряжение на конденсаторе такое же, как на параллельном ему участке цепи.
Ток не проходит через те резисторы, что соединены с конденсатором последовательно. При расчете электрической цепи их сопротивления не учитывают.
Подсказки к задачам
W = q 2 2 C . . = C U 2 2 . .
Пример №5. К источнику тока с ЭДС ε = 9 В и внутренним сопротивлением r = 1 Ом подключили параллельно соединенные резистор с сопротивлением R = 8 Ом и плоский конденсатор, расстояние между пластинами которого d = 0,002 м. Какова напряженность электрического поля между пластинами конденсатора?
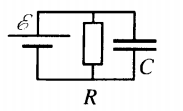
Напряжение на конденсаторе равно напряжению на резисторе, так как он подключен к нему последовательно. Чтобы найти это напряжение, сначала выразим силу тока на этом резисторе:
Применим закон Ома:
Приравняем правые части выражений и получим:
Отсюда напряжение на конденсаторе равно:
Напряженность электрического поля равна:
E = U d . . = ε R d ( R + r ) . . = 9 · 8 0 , 002 ( 8 + 1 ) . . = 72 0 , 018 . . = 4000 ( В м . . )
Текст: Алиса Никитина, 10.1k
Задание EF17564
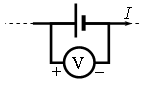
Вольтметр подключён к клеммам источника тока с ЭДС ε = 3 В и внутренним сопротивлением r = 1 Ом, через который течёт ток I = 2 А (см. рисунок). Вольтметр показывает 5 В. Какое количество теплоты выделяется внутри источника за 1 с?
Алгоритм решения




