Для написания любой логической функции может быть использовано логическое выражение, после чего можно составить логическую схему. Как правило, все логические выражения упрощают для получения максимально простой и дешевой логической схемы. В сущности, логическая схема, выражение и логическая функция, являются тремя различными языками, повествующими об одном и том же.
Логические выражения упрощают при помощи различных законов алгебры логики. Часть преобразований напоминает преобразования формул, выполняемые в классической алгебре (например, применение сочетательного и переместительного законов, вынесение за скобки равенства общего множителя и так далее). Для других преобразований используют свойства, которых лишены операции классической алгебры.
Любые законы алгебры логики выводят для главных логических операций следующим образом: НЕ — инверсия (то есть, отрицание); ИЛИ — дизъюнкция (то есть, логическое сложение); И — конъюнкция (то есть, логическое умножение).
Закон двойного отрицания состоит в том, что операция НЕ является обратимой: если ее использовать два раза, логическое значение в результате останется неизменным.
Сущность закона исключенного третьего состоит в том, что каждое логическое выражение при любых условиях является истинным, либо ложным. Если A=1, тогда A=0, а также наоборот. Конъюнкция данных величин всегда равняется 0, дизъюнкция равна 1.
Закон повторения и операции с константами легко можно проверить, используя таблицы истинности операций ИЛИ и И.
Сочетательный и переместительный законы имеют такой же вид, как в математике. Аналогия с привычной всем классической алгеброй.
Для дизъюнкции распределительный закон состоит просто в раскрытии скобок. Для конъюнкции выражение неизвестно, в математике подобное равенство является неверным. Начнем доказывать с правой части. Сначала раскроем скобки:
Используем закон повторение, гласящий, что A⋅A=A,
A+A⋅B=A⋅(1+B)=A⋅1=A, следовательно, (A+B)⋅(A+C)=A+B⋅C.
Мы доказали равенство.
Правил, используемые для раскрытия инверсии сложных выражений, назвали именем известного логика и математика де Моргана. Суть состоит в том, что общее отрицание не только распространяется на отдельные выражения, а еще и дизъюнкция заменяется конъюнкцией (а также наоборот). Для доказательства данных правил используются таблицы истинности.
Основная часть аксиом и законов алгебры логики записаны попарно. Внимательно изучая пары, можно сформулировать принцип двойственности, звучащий следующим образом: если осуществить в тождестве замены конъюнкции, а также дизъюнкции. И также элементов 1 и 0 (при их наличии), получится тождество. Данное свойство именуют принципом двойственности.
Так и не нашли ответ на вопрос?
Просто напишите,с чем нужна помощь
Мне нужна помощь
Упрощения логических выражений в примерах
Формула, вытекающая из распределительного закона. При ее выведении применили вышеупомянутое правило де Моргана для дизъюнкции, а также использовали закон двойного отрицания, после чего сомножитель X, вынесли за скобку, тогда как в скобках получили закон исключённого третьего, а также применили операцию с константами.
Построение таблиц истинности
Лень читать?
Задай вопрос специалистам и получи ответ уже через 15 минут
Задать вопрос
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2 n , где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Пример 1. Для формулы A/ (B / ¬B /¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
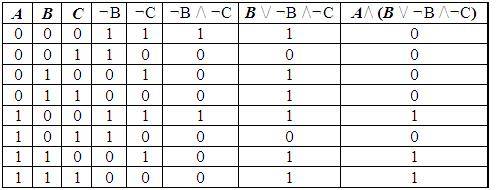
Пример 2. Определите истинность логического выражения F(А, В) = (А/ В)/(¬А/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2 n , m=2 2 =4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А/ В; 2) ¬А; 3) ¬В; 4) ¬А/¬В; 5) (А/ В)/(¬А/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А
В
А/ В
¬А
¬В
¬А/¬В
F
0
1
1
0
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A/ B) / ¬С
- В данной функции три логические переменные – А, В, С
- количество строк таблицы = 2 3=8
- В формуле 3 логические операции.
- Расставляем порядок действий
1) А/ В; 2) ¬С; 3) (AVB) / ¬С .
- количество столбцов таблицы = 3 + 3 = 6
А
В
С
A/B
(A/B) / ¬С
0
0
1
0
1
0
1
0
Пример 4. Определите истинность формулы: F = ((С /В) => В) / (А / В) => В.
Построим таблицу истинности этой формулы.
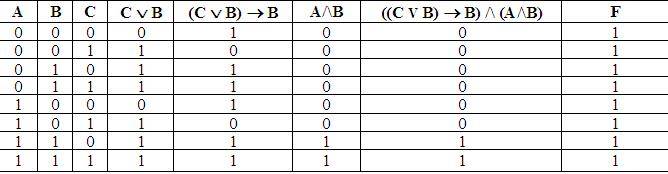
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
X
Y
Z
F
¬X/¬Y/Z
¬X/¬Y/Z
X/Y/¬Z
X/Y/Z
1
1
0
0
1
1
Очевидно, что значения заданной функции F совпадают со значениями выражения X/Y/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/¬Y/Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X/¬Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X/Y/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X/Y/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Влияние на работу компьютера
Логические операции составляют основу работы вычислительных систем. На физическом уровне компьютеры основаны на транзисторах, которые могут находиться в одном из двух состояний: открытое (проводящее) или закрытое (непроводящее). Эти состояния соответствуют логическим значениям истина и ложь.
Комбинации транзисторов могут выполнять базовые логические операции, такие как инверсия, конъюнкция и дизъюнкция. Таким образом, при помощи логических операций компьютеры могут выполнять сложные алгоритмы, принимать решения и обрабатывать информацию.
В программировании логические выражения используются для создания условных конструкций, циклов и других элементов управления потоком выполнения программы.
Понимание логических операций и их свойств критически важно для изучения информатики. Они являются основой для разработки алгоритмов, программирования и, в конечном итоге, для всего, что делает компьютер таким мощным инструментом.
3. Равносильные логические выражения
Логические выражения, у которых последние столбцы таблиц истинности сов- падают, называются равносильными. Для обозначения равносильных логических выражений используется знак « = ». Докажем, что логические выражения  равносильны. Построим сначала таблицу истинности логического выражения
равносильны. Построим сначала таблицу истинности логического выражения  (табли- ца 9). Таблица 9 – Таблица истинности логического выражения
(табли- ца 9). Таблица 9 – Таблица истинности логического выражения 
| А | В | |||
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |

Теперь построим таблицу истинности логического выражения (таблица 10). Таблица 10 – Таблица истинности логического выражения
| А | В | А v В | |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
Значения в последних столбцах таблиц истинности совпадают, следовательно, логические выражения равносильны:  =
=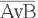 .
.
Построение таблиц истинности для сложных выражений
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы. Для формулы, которая содержит две переменные, таких наборов значений
| переменных всего четыре: | |||
| (0, 0), | (0, 1), | (1, 0), | (1, 1). |
Если формула содержит три переменные, то возможных наборов значений
| переменных восемь: | |||||||
| (0, 0, 0), | (0, 0, 1), | (0, 1, 0), | (0, 1, 1), | (1, 0, 0), | (1, 0, 1), | (1, 1, 0), | (1, 1, 1). |
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д. Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул. Пример 1 1. Составим таблицу истинности для формулы, которая содержит две пере- менные X и Y . В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу 11: Таблица 11 – Таблица истинности для формулы с переменными Х и У Пример 2 Cоставить таблицу истинности сложного логического выражения: D = неA если заданы только 6 из них, то можно найти 2 8−6 = 2 2 = 4 разные логические функции, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся).
Очень хорошей помощью в решении этого задания будет полная таблица истинности данного в условии логического выражения.
Полную таблицу истинности легче всего составить в табличном редакторе (Excel) или с использованием языка программирования (Python).
После получения полной таблицы истинности остается провести анализ на соответствие строк данной в условии части таблицы строкам составленной. При анализе строк особое внимание следует обратить на значение выражения в таблице истинности.
Если выражение равно 0, то нужно постараться привести данное в условие выражение к виду A + B + C + … . Логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно).
Если выражение равно 1, то приводите выражение к виду A · B · C · … . Логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно).
И еще два факта, которые пригодятся при анализе: логическое следование (импликация) А → В равно 0 тогда и только тогда, когда A (посылка) истинна, а B (следствие) ложно; эквивалентность А º B равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1.
Используем 3 способа решения задания
Способы решения задания:
- ручной;
- с помощью электронных таблиц;
- с помощью языка программирования (Python).
Ручной способ решения
При ручном способе решения особенно важно сначала упростить выражение, данное в условии задачи, то есть привести логическое выражение к такому виду, который будет удобнее анализировать.
Например, если в условии представлена часть таблицы истинности, в которой значение выражения равно 1 — то можно постараться привести логическое выражение к нормальной дизъюнктивной форме (ДНФ — произведение нескольких литералов). Тогда выражение будет истинным, только если каждый литерал (сомножитель) будет истинен.
Если же в таблице истинности логическое выражение равно 0 — приводим выражение к нормальной конъюнктивной форме (КНФ — сумма нескольких литералов). В этом случае выражение будет ложным, только если каждый литерал (слагаемое) ложен.
После преобразования логического выражения производится анализ данной в условии таблицы истинности (или ее фрагмента) и для каждого столбца находится его значение (x, y и т. д.)
Решение с помощью электронных таблиц
При использовании электронных таблиц самым сложным является ввод в ячейку таблицы выражения, данного в условии в нотации, соответствующей программе. Чаще всего в качестве программ электронных таблиц используются электронные таблицы пакетов Libre Office, Open Office или Microsoft Office (Excel). Последняя — наиболее распространенная, поэтому здесь будем говорить про нее.
Шаг 1. Сначала количество столбцов в электронной таблице равно количеству переменных логического выражения. Каждый столбец обозначается по именам переменных логического выражения.
Шаг 2. Затем добавляется количество строк электронной таблицы, равное , где k — количество переменных логического уравнения.
Шаг 3. После этого создается еще один столбец электронной таблицы, в первой строке которого (не заголовка) записывается формула, соответствующая логическому выражению. Растянув эту формулу при помощи маркера автозаполнения на все строки таблицы, получаем полную таблицу истинности выражения.
Таблица функций электронной таблицы Excel и их соответствия логическим операциям:
| Логическая операция | Строка Excel |
| Инверсия | =ЕСЛИ(A2=1;0;1) |
| Дизъюнкция | =ЕСЛИ(ИЛИ(A2=1;B2=1);1;0) |
| Конъюнкция | =ЕСЛИ(И(A2=1;B2=1);1;0) |
| Импликация | =ЕСЛИ(И(A2=1;B2=0);0;1) |
| Эквивалентность | =ЕСЛИ(A2=B2;1;0) |
Решение с помощью языка программирования (Python)
При использовании программы на языке Python можно описать функцию, например так:
def f(arg):
x, y, z, w = arg
return (здесь записывается логическое выражение),
а затем, используя полный переборный алгоритм, перебрать значения 0 и 1 для каждой переменной во вложенных циклах и провести проверку истинности выражения:
print (‘x y w z’) # заголовок таблицы (в алфавитном порядке)
k = 0, 1 # k — кортеж констант (0 — False, 1 — True)
for x in k:
for y in k:
for w in k:
for z in k:
if f(x, y, w, z) == 1:
print(x, y, w, z) # если F = 1
Или просто вывести таблицу истинности print(x, y, w, z), не используя условный оператор во внутреннем цикле.
Полученную таблицу истинности остается проанализировать вручную и записать единственно верный ответ.
Для того чтобы записать логическое выражение на Python, воспользуйтесь следующей таблицей:
| Обозначение | Название | Оператор в Python |
| ∧ | конъюнкция | and |
В Python логическое значение True воспринимается как 1, а False — как 0, благодаря этому можно использовать обычное умножение *
| ∨ | дизъюнкция | or |
В Python логическое значение True воспринимается как 1, а False — как 0, благодаря этому можно использовать обычное сложение +
| ¬ | отрицание | not() |
| ≡ | тождество | == |
| ⊕ | строгая дизъюнкция | != |
| → | импликация | not(a) or b или not a or b или a |
Желаем вашим ученикам высоких баллов по ЕГЭ!
Таблицы и операции
Построить таблицу истинности можно без онлайн калькуляторов. Для этого достаточно запомнить, как работает каждая из перечисленных выше операций. У математиков с этим проблем не возникает – они хорошо заучивают предложенную далее информацию.
Конъюнкция
Носит название «логическое И» или «умножение». Часто встречается в программировании. В языках «создания контента» обладает особым обозначением. Примеры записи:
Выражение логического характера при конъюнкции является истиной, только когда оба простых высказывания тоже выступают в качестве правды. Если хотя бы одно из них – ложь, то вся операция примет значение False.
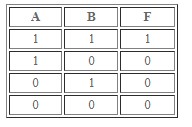
Выше представлена таблица истинности при операции конъюнкции.
Дизъюнкция
Является сложением. У этого логического выражения есть иное название – «логическое ИЛИ». Тоже встречается в программировании довольно часто.
Может иметь такие формы записи:
Преобразование последовательности будет осуществляться по принципу: выражение – истина, если хотя бы одно из его составляющих – правда. Ложно, когда оба элемента имеют значение FALSE.
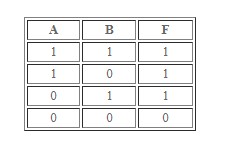
Выше – примеры таблицы истинности, которая работает в отношении дизъюнкции.
Инверсия
Следующий момент, на который стоит обратить внимание – это инверсия. Носит название «отрицание» или «логическое НЕ».
Обозначения в программировании:
Логическое выражение при отрицании обладает следующими особенностями:
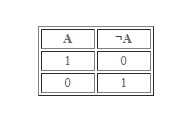
- Когда исходные данные истины, то результатом станет ложь.
- Если операция обладает значением «ложь», ее отрицание получит «истину».
- Можно рассматривать соответствующую манипуляцию как трактовку «Неверно, что…»
Вот такую таблицу истинности можно построить относительно инверсии.
Импликация
При любом логическом выводе стоит опираться на предлагаемые примеры и таблицы. Импликация – это следование.
В любом заданном логическом выражении результат – это истина всегда. Исключение – когда из правды следует ложь. Она связывает два высказывания (a и b), где:
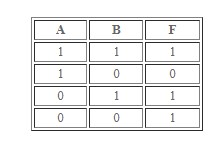
- A – это условие, первое выражение;
- B – следствие.
Если из A может следовать B, значит операция выдаст в результате обработки «истину».
Эквивалентность
Так называют равнозначность. Новое высказывание истинно тогда, когда оба простых выражения – это правда.
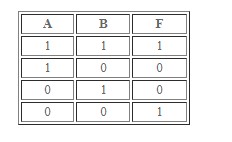
Выше – пример расчетов формулы логики заданных высказываний при эквивалентности.
Исключение
Онлайн калькуляторы могут помочь построить график или указать, что верно, а что нет, без вдумчивости в поставленную задачу со стороны пользователя. Но программистам приходится прописывать принципы функционирования и выполняемые операции вручную. Для них особенности алгебры логики и информатики крайне важны.
Порядок выполнения логических операций ранее был рассмотрен. Осталось понять, как работает исключение.
Согласно установленным правилам, операция будет истиной, когда среди значений переменных A и B есть одно правдивое. Если оба – это действительность, упомянутый принцип работать не будет.
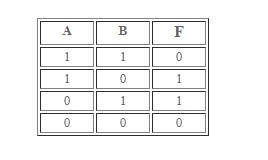
Исключающее ИЛИ – преобразование, которое носит название «сложение по модулю два».
Законы алгебры логики
Формулы логики высказываний запомнить не так трудно. Но учить соответствующие законы – не всегда оправданный шаг. Для выполнения операций достаточно вспомнить алгебру, а также преобразование выражений.
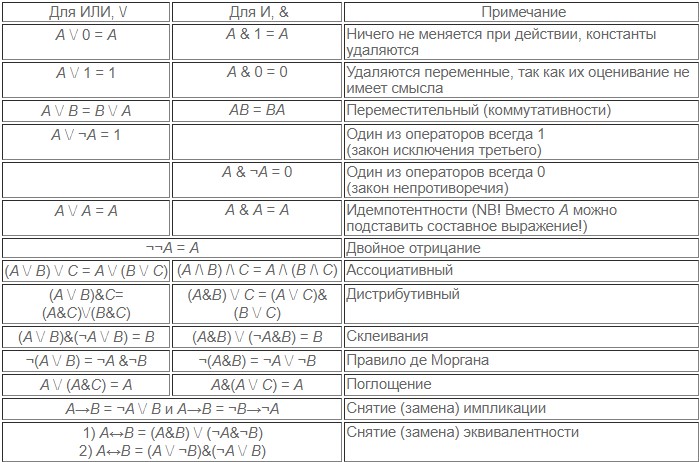
Выше – примеры логических операций, упрощенные для запоминания человеком.
Пример задания
Пусть необходимо построить таблицу для логического выражения F = (A → B) * (A + B). Эта формула состоит из двух логических переменных A и B и нескольких операций. Начинают построение с определения строк. Используя формулу 2n+1 для рассматриваемого примера можно установить, что их число будет: x = 22 + 1 = 5.
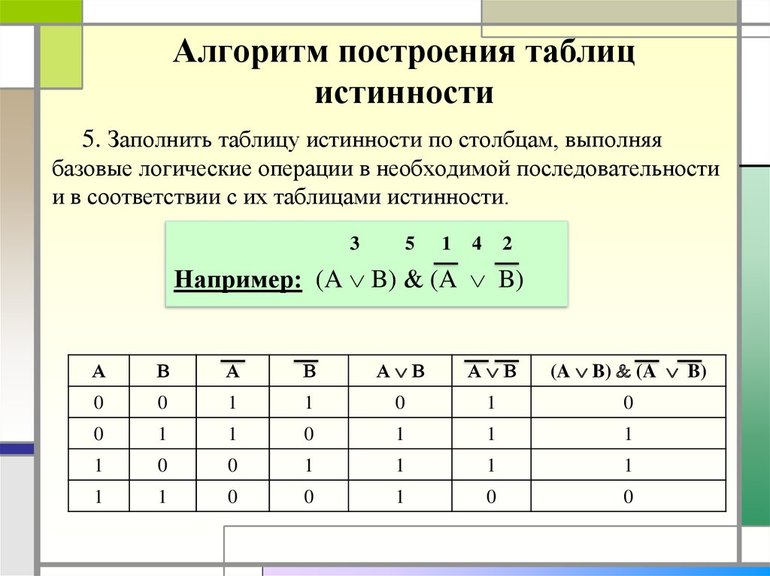
Теперь следует определить число столбцов. Для этого используется формула, в которой учитывается количество переменных и операций. Последние можно просто посчитать, сложив количество разных знаков, используемых в записи формулы. Но правильней сначала расставить порядок операций, а затем посчитать. Согласно порядку действия над операциями их нумерацию можно представить в следующей очерёдности:
- Импликация в первой скобке.
- Инверсия во второй скобке переменной A.
- Отрицание во второй скобке неизвестной B.
- Сложение во втором члене.
- Конъюнкция.
В итоге получится, что столбцов будет: Y = 2 + 5 = 7. Теперь нужно построить таблицу 7Х5. В шапку первого и второго столбца вписывают переменные, а затем операции над ними. Затем в строках, соответствующих A и B нужно записать всё, что с ними может произойти. В итоге останется только правильно посчитать последний столбец.
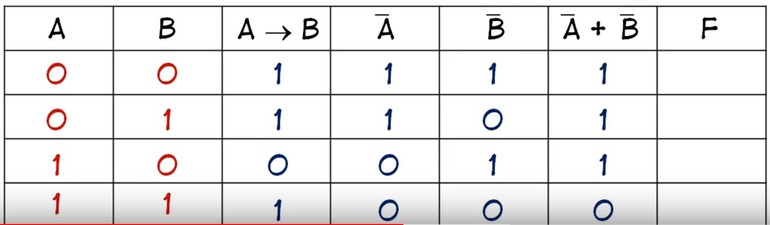
Для этого нужно использовать законы. Необходимо выполнить логическое умножение значений в скобках. Первой и второй строчке будет соответствовать операция произведения один на один, что в ответе даст единицу. Третьей и четвёртой — ноль на один, что в итоге даст ноль. Последний столбец является главным для рассматриваемой логической функции. По нему можно узнать значение логической функции для любых форм переменных A и B.
Это довольно простая задача, содержащая всего две переменных. Но в реальности, например, в программировании, их может быть намного больше. Решать такие задания методом перебора проблематично. Поэтому при решении сложных примеров функцию вначале пытаются упростить.
Например, заданно выражение (x + y + z) * (x + y). По сути, оно записано в совершенно нормальной конъюнктивной форме. Но для приведения его к этому виду нужно, чтобы во втором выражении стояла z. Для того чтобы её добавить необходимо обратить внимание на то, что внутри скобок стоит логическое сложение. Поэтому дописав к нему ноль, результат не изменится. Добавить ноль через z можно, как ноль умножить на НЕ z. В итоге получится выражение (x + y + z) * (x + y + z + z), для которого, используя алгоритм составить таблицу уже не так и сложно.
Вычисления онлайн
В интернете есть сервисы, автоматически строящие таблицы истинности. Такие сайты предлагают свои услуги бесплатно и доступны даже тем, кто слабо ориентируется в теме. С их помощью можно находить таблицы для довольно сложных выражений, решение которых требует скрупулёзности в расчёте. В основе онлайн-вычислений заложены принципы логических законов, поэтому за достоверность результата можно не переживать. Тем более расчёт занимает совсем небольшое количество времени.
Для того чтобы воспользоваться сайтами-калькуляторами пользователю необходимо знать обозначение операций, иметь подключение к интернету и установленный веб-обозреватель, поддерживающий Flash-технологию. Регистрацию, указание личных данных сервисы, предлагающие такого рода услуги, не требуют.
Из различных порталов можно отметить три наиболее популярных калькулятора:
- Allcalc.
- Programforyou.
- Uchim.
Эти сайты имеют интуитивно понятный интерфейс и что довольно полезно, на своих страницах содержат краткую теорию, используемую для составления таблиц истинности и даже примеры решений.




