Сегодня нас ждёт увлекательный эксперимент: мы перейдём от этапа «вообще не понимаю, что это» к «надо же, как всё просто и логично» всего за одну статью. Не верите? Мы вам обещаем! Мы поговорим о колебательных контурах, электромагнитных волнах и том, как мы встречаемся с этими понятиями в обычной жизни.
· Обновлено 28 июля 2023
Колебания
Начнём обсуждение этой темы с колебаний. В обычной жизни мы часто слышим это слово: «цветок колеблется на ветру», «я не могу принять решение, колеблюсь», «температура воздуха колеблется в диапазоне…». Но что такое колебания в физике?
Колебания — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия.
Попробуйте привести несколько примеров такого движения. Верно, к колебаниям можно отнести движение стрелки, вращение качели, качание маятника часов.
Колебания бывают вынужденными и свободными.
- Вынужденные колебания — это колебания, происходящие под действием внешней периодически меняющейся силы. Посадите свою маленькую сестрёнку или братишку на качели: раскачивая их, вы станете той самой внешней силой, под действием которой качели движутся, совершая при этом вынужденные колебания.
- Свободные колебания — это колебания, происходящие под действием внутренних сил в колебательной системе. Груз колеблется на нити или пружине — вот самый распространённый пример свободных колебаний. Такие колебания всегда затухающие, потому что ни у одной системы нет бесконечного запаса энергии для такого движения: рано или поздно колебание прекратится.
Что может совершать свободные колебания? Математический (груз + нить) и пружинный (груз + пружина) маятники, а также электромагнитные волны.

Колебательный контур — что это такое и как он работает
Электрический колебательный контур является обязательным элементом любого радиоприемника, независимо от его сложности. Без колебательного контура прием сигналов радиостанции вообще невозможен.
Простейший электрический колебательный контур (рис. 20) представляет собой замкнутую цепь, состоящую из катушки индуктивности L и конденсатора С. При некоторых условиях в нем могут возникать и поддерживаться электрические колебания.

Чтобы понять сущность этого явления, проведи сначала несколько опытов с нитяным маятником (рис. 21). На нитке длиной 100 см подвесь шарик, слепленный из пластилина, или иной грузик массой в 20. 40 г.
Выведи маятник из положения равновесия и, пользуясь часами с секундной стрелкой, сосчитай, сколько полных колебаний он делает за минуту. Примерно 30. Следовательно, собственная частота колебаний этого маятника равна 0,5 Гц, а период (время одного полного колебания) — 2 с. За период потенциальная энергия маятника дважды переходит в кинетическую, а кинетическая в потенциальную.
КАК РАБОТАЕТ КОЛЕБАТЕЛЬНЫЙ КОНТУР
Укороти нить маятника наполовину. Собственная частота колебаний маятника увеличится в полтора раза и во столько же уменьшится период колебаний. Вывод: с уменьшением длины маятника частота его собственных колебаний увеличивается, а период пропорционально уменьшается.
Изменяя длину подвески маятника, добейся, чтобы его собственная частота колебаний составляла 1 Гц (одно полное колебание в секунду). Это должно быть при длине нитки около 25 см. В этом случае период колебаний маятника будет равен 1 с.
Колебания нитяного маятника являются затухающими. Свободные колебания любого тела всегда затухающие. Они могут стать незатухающими только в том случае, если маятник в такт с его колебаниями слегка подталкивать, компенсируя таким образом ту энергию, которую он затрачивает на преодоление сопротивления, оказываемого ему воздухом и силой трения.
Частота собственных колебаний маятника зависит от его массы и длины подвески.
Теперь натяни горизонтально нетолстую веревку или шпагат. Привяжи к растяжке тот же маятник (рис. 22). Перекинь через веревку еще один такой же маятник, но с более длинной ниткой. Длину подвески этого маятника можно изменять, подтягивая рукой свободный конец нитки.
Приведи его в колебательное движение. При этом первой маятник тоже станет колебаться, но с меньшим размахом (амплитудой). Не останавливая колебаний второго маятника, постепенно уменьшай длину его подвески — амплитуда колебаний первого маятника будет увеличиваться.

В этом опыте, иллюстрирующем резонанс колебаний, первый маятник является приемником механических колебаний, возбуждаемых вторым маятником — передатчиком этих колебаний. Причиной, вынуждающей первый маятник колебаться, являются периодические колебания растяжки с частотой, равной частоте колебаний второго маятника. Вынужденные колебания первого маятника будут иметь максимальную амплитуду лишь тогда, когда его собственная частота совпадает с частотой колебаний второго маятника.
Собственная частота, вынужденные колебания и резонанс, которые ты наблюдал в этих опытах, — явления, свойственные и электрическому колебательному контуру.
Электрические колебания в контуре. Чтобы возбудить колебания в контуре, надо его конденсатор зарядить от источника постоянного напряжения, а затем отключить источник и замкнуть цепь контура (рис. 23).
С этого момента конденсатор начнёт разряжаться через катушку индуктивности, создавая в цепи контура нарастающий по силе ток; а вокруг катушки индуктивности — магнитное поле тока. Когда конденсатор полностью разрядится и ток в цепи станет равным нулю, магнитное поле вокруг катушки окажется наиболее сильным — электрический заряд конденсатора преобразовался в магнитное поле катушки.
Ток в контуре некоторое время булет идти в том же направлении, но уже за счет убывающей энергии магнитного поля, накопленной катушкой, а конденсатор начнет заряжаться. Как только магнитное поле катушки исчезнет, ток в контуре на мгновение прекратится.
Но к этому моменту конденса-fop окажется перезаряженным, поэтому в цепи контура вновь пойдет ток, но уже в противоположном направлении. В результате в контуре возникают колебания электрического тока, продолжающиеся до тех пор, пока энергия, запасенная конденсатором, не израсходуется на преодоление сопротивления проводников контура.
Электрические колебания, возбужденные в контуре зарядом конденсатора, свободные, а следовательно, за-тухающие. Зарядив снова конденсатор, в контуре мож-но возбудить новую серию затухающих колебаний.
Подключи к батарее 3336Л электромагнитные головные телефоны. В момент замыкания цепи в телефонах появится звук, напоминающий щелчок. Такой же щелчок слышен и в момент отключения телефонов от батареи.
Заряди от этой батарей бумажный конденсатор возможно большей емкости, а затем, отключив батарею, подключи к нему те же телефоны. В телефонах услышишь короткий звук низкого тона. Но в момент отключения телефонов от конденсатора такого звука не будет.
В первом из этих опытов щелчки в телефонах являются следствием одиночных колебаний их мембран при изменении силы магнитных полей катушек электромагнитных систем телефонов в моменты появления и исчезновения тока в них.
Во втором опыте звук в телефонах — это колебания их мембран под действием переменных магнитных полей катушек телефонов. Они создаются короткой очередью затухающих колебаний очень низкой частоты, возбужденных в. этом контуре после подключения заряженного конденсатора.
Собственная частота электрических колебаний в контуре зависит от индуктивности его катушки и емкости конденсатора. Чем они больше, тем ниже частота колебаний в контуре и, наоборот, чем они меньше, тем выше частота колебаний в контуре. Изменяя индуктивность (число витков) катушки и емкость конденсатора, можно в широких пределах изменять частоту собственных электрических колебаний в контуре.
Чтобы вынужденные колебания в контуре были незатухающими, контур в такт с колебаниями в нем надо пополнять дополнительной энергией. Для приемного контура источником этой энергии могут быть электрические колебания высокой частоты, индуцируемые радиоволнами в антенне радиоприемника.

Контур в радиоприемнинике. Если к колебательному контуру подключить антенну, заземление и цепь, составленную из диода, выполняющего роль детектора, и телефонов, то получится простейший радиоприемник — детекторный (рис. 24).
Для колебательного контура такого приемника используй катушку индуктивности, намотанную тобой еще при прохождении третьего практикума. Конденсатор переменной емкости (G2) для плавной и . точной настройки контура на частоту радиостанции сделай из двух жестяных пластин, припаяв к ним проводники. Между пластинами, чтобы они не замыкались, положи лист сухой писчей или газетной бумаги.
Емкость такого конденсатора будет тем больше, чем больше площадь взаимного перекрытия пластин и чем меньше расстояние между ними. При размерах пластин 150X250 мм и расстоянии между ними, равном толщине бумаги, наибольшая емкость та?-кого конденсатора может быть 400. 450 пФ, что тебя вполне устроит, а наименьшая несколько пикофарад.
Антенной-времянкой (W1) может служить хорошо изолированный от земли и от стен здания отрезок провода длиной 10. 15 м, подвешенный на высоте 10. 12 м. Для заземления можно использовать металлический штырь, вбитый в землю, трубы водопровода или центрального отопления, имеющие, как правило, хороший контакт с землей.
Роль детектора (VI) может выполнять точечный диод, например, серии Д9 или Д2 с любым буквенным индексом. В1 — головные телефоны электромагнитные, высоко-омные (с катушками электромагнитов сопротивлением постоянному току 1500. 2200 Ом), например, типа ТОН-1. Параллельно телефонам подключи конденсатор (C3) емкостью 3300. 6200 пФ.
Все соединения должны быть электрически надежными. Лучше, если они пропаяны. Из-за плохого контакта в любом из соединений приемник работать не будет. Приемник не будет работать и в том случае, если в его цепях будут короткие замыкания или неправильные соединения.
Настройка контура приемника на частоту радиостанции осуществляется: грубая — скачкообразным измене-нием числа витков катушки, включаемых в контур (на рис. 24 показано штриховой линией со стрелкой); плав-ная и точная — изменением емкости конденсатора путем смещения одной из его пластин относительно другой.
Если в городе, крае или области, где ты живешь, работает радиостанция длинноволнового диапазона (735,3. 2000 м, что соответствует частотам 408. 150 кГц), то в контур включай все витки катушки, а если станция средневолнового диапазона (186,9. 571,4 м, что собтвет-ствует частотам 1,608 МГц.„525 кГц), то только часть ее витков.
При одновременной слышимости передач двух радиостанций включи между антенной и контуром конденсатор емкостью 62. 82 пФ (на рис. 24 — конденсатор С1, показанный штриховыми линиями). От этого громкость звучания телефонов несколько снизится, но селективность (избирательность) приемника, то есть его спог собность отстраиваться от мешающих станций, улучшится.
Как работает такой приемник в целом? Модулированные колебания высокой частоты, индуцируемые-в проводе антенны радиоволнами многих станций, возбуждают в контуре приемника, в который входит и сама антенна, колебания разных частот и амплитуд.
В контуре же возникнут наиболее сильные колебания только той частоты, на которую он настроен в резонанс. Колебания всех других частот контур ослабляет. Чем лучше (добротнее) контур, тем четче он выделяет колебания, соответствующие колебаниям его собственной частоты, и больше их амплитуда.
Детектор также важный элемент приемника. Обладая односторонней проводимостью тока, он выпрямляет высокочастотные модулированные колебания, поступающие к нему от колебательного контура, преобразуя их в колебания низкой, то есть звуковой, частоты, которые телефоны преобразуют в звуковые колебания.
Конденсатор C3, подключенный параллельно телефонам, — вспомогательный элемент приемника: сглаживая пульсации тока, выпрямленного детектором, он улучшает условия работы телефонов.
Проведи несколько экспериментов.
1. Настроив приемник на радиостанцию, введи внутрь катушки толстый гвоздь, а затем конденсатором переменной емкости подстрой контур, чтобы восстановить прежнюю громкость звучания телефонов.
2. Сделай то же самое, но вместо гвоздя возьми медный или латунный стержень.
3. Подключи к контурной катушке вместо конденсатора переменной емкости такой конденсатор постоянной емкости (подбери опытным путем), чтобы приемник оказался настроенным на частоту местной станции.
Запомни конечные результаты этих экспериментов. Вводя внутрь катушки металлический сердечник, ты, конечно, заметил, что собственная частота контура при этом изменяется: стальной сердечник уменьшает собственную частоту колебаний в контуре, а медный или латунный, наоборот, увеличивает. Судить об этом можно по тому, что в первом случае для подстройки контура на сигналы той же станции емкость контурного конденсатора пришлось уменьшить, а во втором увеличить.
Контурная катушка с высокочастотным сердечником. Подавляющее большинство контурных катушек современных приемников имеет высокочастотные, обычно ферритовые, сердечники в виде стержней, чашек или колец.
Ферритовые стержни, кроме того, являются обязательными элементами вхрдных контуров всех транзисторных переносных и так называемых «карманных» приемников.

Высокочастотный сердечник как бы «сгущает» линии магнитного поля катушки, повышая ее индуктивность и добротность. Подвижный сердечник, кроме того, позволяет регулировать индуктивность катушки, что используют для подстройки контуров на заданную частоту, а иногда даже настраивать контуры на частоты радиостанций.
В порядке эксперимента сделай приемник с колебательным контуром, настраиваемым ферритовым стержнем марки 400НН или 600НН длиной 120. 150 мм (рис. 25). Такие стержни используют Для магнитных антенн транзисторных приемников.
Из полоски бумаги, обернув ею стержень 3. 4 раза, склей и хорошо просуши гильзу длиной 80. 90 мм. Внутрь гильзы стержень должен входить свободно. Вырежь из картона 9. 10 колец и приклей их к гильзе на расстоянии 6. 7 мм друг от друга.
На получившийся секционированный каркас -намотай 300. 350 витков лровода ПЭВ, ПЭЛ или ПЭЛШО 0,2. 0,25, укладывая его по 35. 40 витков в каждой секции. От 35. 40-го -и от 75. 80-го витков сделай два отвода в виде петель, чтобы иметь возможность изменять число витков катушки, включаемых в контур.
Подключи к катушке антенну, заземление и цепь детектор — телефоны. Чем больше витков катушки будет участвовать в работе контура и глубже внутрь катушки будет введен ферритовый стержень, тем на большую длину волны может быть настроен приемник.
Детекторный приемник работает исключительно благодаря электромагнитной энергии, излучаемой антенной передатчика радиостанции. Поэтому телефоны звучат негромко. Чтобы повысить громкость работы детекторного приемника, к нему надо добавить усилитель, например транзисторный.
Литература: Борисов В. Г. Практикум начинающего радиолюбителя.2-е изд., перераб. и доп. 1984.
Резонанс LC-контура
Электромагнитные колебания в LC-контуре происходят с определенной частотой, которая называется резонансной Подробнее про резонанс – в нашей отдельной статье. Частоту колебаний можно менять, варьируя такие параметры контура, как емкость конденсатора C, индуктивность катушки L, сопротивление резистора R (для LCR-контура).
Как рассчитать резонансную частоту колебательного контура? Очень просто! Приведем окончательную формулу:
Применение колебательного контура
Колебательный контур широко применяется на практике. На его основе строятся частотные фильтры, без него не обходится ни один радиоприемник или генератор сигналов определенной частоты.
Если вы не знаете, как подступиться к расчету LC-контура или на это совершенно нет времени, обратитесь в профессиональный студенческий сервис. Качественная и быстрая помощь в решении любых задач не заставит себя ждать!
Параллельный и последовательный колебательный контур
Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных параметров. Онлайн калькулятор резонансной частоты колебательного контура, добротности и коэффициента затухания в зависимости от величин индуктивности, ёмкости и сопротивления потерь
Колебательный контур – это пассивная электрическая цепь, которая состоит из конденсатора и катушки индуктивности, в которой возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный контур называется последовательным.
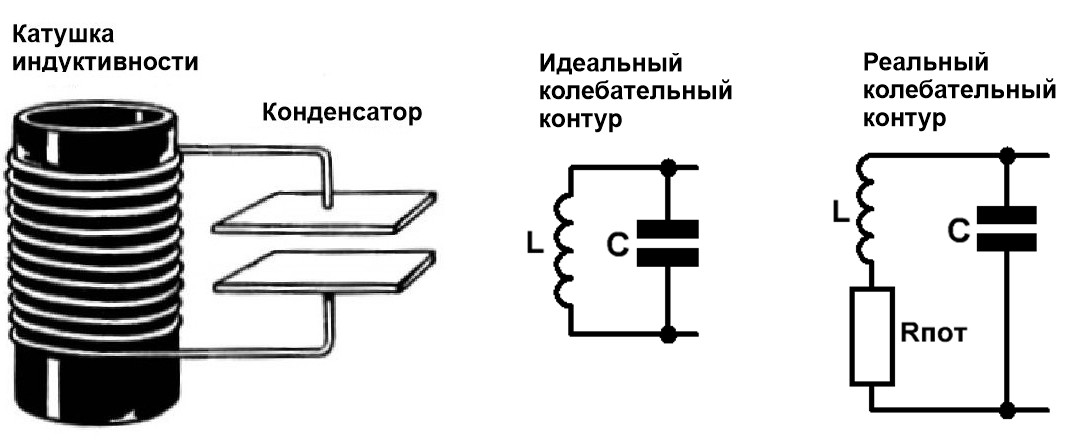
Для начала давайте рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного.
Рис.1 Параллельный колебательный контур, его изображение на схеме
(идеальный колебательный контур), реальный колебательный контур
При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного сопротивления потерь катушки – Rпот . Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.
Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)
Рис.2 Колебательный процесс в параллельном колебательном контуре
Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд qmax от внешнего источника Bat напряже- нием Umax . После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).
Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь, суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.
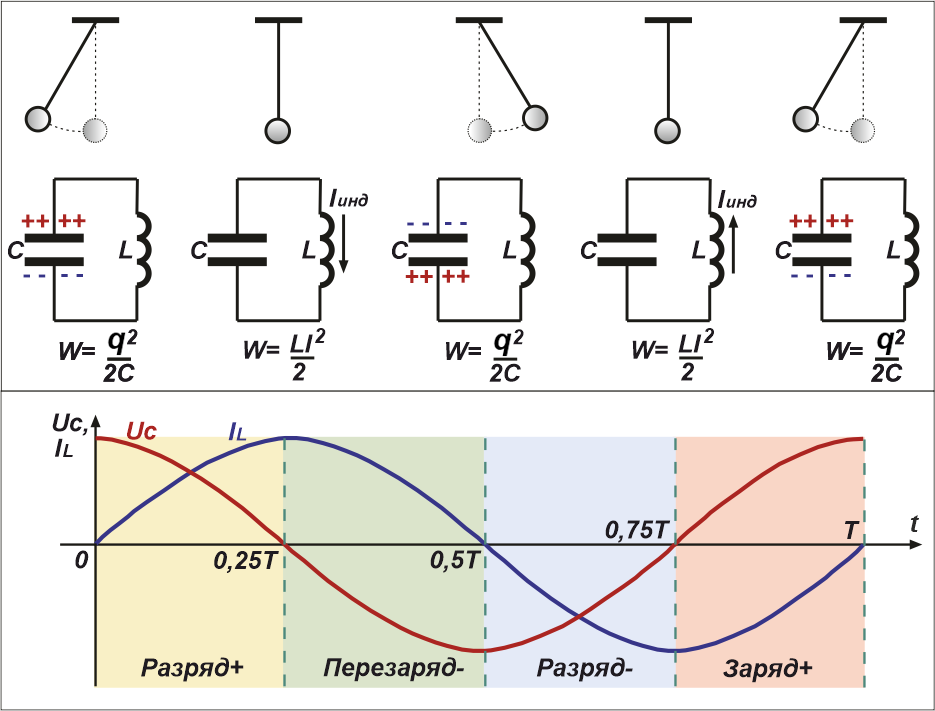
Рис.3 Фазы колебаний в колебательном контуре за полный период
Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.
Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна W = q 2 /2C ). Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС самоиндукции, препятствующая этому росту.
2. t = 0.25Т – конденсатор полностью разряжен. Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки W = L*I 2 /2 . Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0.5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0.75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.
А теперь: Формулы для расчёта колебательного LC контура:
Период колебаний: T0 = 2π√ LC ;
Частота: F0 = 1/T0 ;
Круговая (циклическая) частота: ω0 = 2π/T0 = 2πF0 ;
Максимальный заряд конденсатора: qmax = UmaxC ;
Максимальная сила тока через катушку: Imax = ωqmax .
Добротность колебательного контура: ;
Мгновенные значения напряжения, тока и энергии рассчитываются по формулам:
Заряд: q(t) = qmax cos(ωt) ;
Напряжение: U(t) = Umax cos(ωt) ;
Сила тока: I(t) = Imax sin(ωt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) .
Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров (с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания β и логарифмический декремент колебаний λ .
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно пропорциональная времени τ , по истечении которого амплитуда колебаний убывает в е раз. Для колебательного контура данная величина вычисляется по формуле: β = Rпотерь /(2L) .
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент равен коэффициенту затухания, умноженному на период колебаний: λ = βT .
С учётом коэффициента затухания формулы приобретают следующий вид:
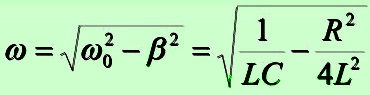
Заряд: q(t) = qmax cos(ωt) e (-βt) ;
Напряжение: U(t) = Umax cos(ωt) e (-βt) ;
Сила тока: I(t) = Imax sin(ωt) e (-βt) ;
Энергия: W(t) = I(t) 2 L/2 + q(t) 2 /(2C) ;
Период: ;
Круговая (циклическая) частота: ;
Добротность: Q = Lω/R .
При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие β 2 2 , круговая частота контура равна ω ≈ ω0 , а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.
Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.
Расчёт резонансной частоты, добротности и коэффициента
затухания контура
Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.
А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.
Применение колебательных контуров
Колебательные контуры широко применяются в различных областях электроники и радиотехники. Они играют важную роль в создании различных устройств и систем. Рассмотрим некоторые области применения колебательных контуров:
Роль колебательных контуров в радиосвязи
В радиосвязи колебательные контуры используются для настройки и фильтрации сигналов. Они позволяют выбирать определенные частоты для передачи или приема сигналов. Например, в радиоприемниках колебательные контуры используются для выбора и усиления сигналов определенной частоты, а для передачи сигналов в радиопередатчиках они помогают формировать и усиливать сигналы передаваемой частоты.
Использование колебательных контуров в фильтрах
Колебательные контуры также широко применяются в фильтрах для выборочной передачи или подавления определенных частот. Фильтры на основе колебательных контуров могут быть использованы, например, для подавления шумов или помех в электрических сигналах. Они позволяют пропускать только сигналы определенной частоты и подавлять остальные.
Применение колебательных контуров в генераторах сигналов
Колебательные контуры используются в генераторах сигналов для создания стабильных и точных сигналов определенной частоты. Они позволяют генерировать сигналы с высокой стабильностью и точностью, что является важным для многих приложений, таких как измерения, тестирование и связь.
Это лишь некоторые примеры применения колебательных контуров. Они также используются в других областях, таких как радары, медицинская техника, аудио- и видеоаппаратура и многие другие.
Практические примеры использования колебательного контура
Схема Реле Шмидта
Схема Реле Шмидта – это пример использования колебательного контура для создания устойчивого переключателя сигнала. Она состоит из операционного усилителя, резисторов, конденсаторов и обратной связи через колебательный контур.
Когда входной сигнал превышает определенный пороговый уровень, колебательный контур начинает колебаться, создавая положительную обратную связь, которая усиливает сигнал и переводит его в высокое состояние. Когда входной сигнал падает ниже порогового уровня, колебательный контур перестает колебаться, и обратная связь становится отрицательной, переводя сигнал в низкое состояние.
Схема Реле Шмидта широко используется в электронике для создания стабильного и надежного переключателя сигнала. Она может быть использована, например, для обнаружения уровня сигнала, фиксации состояния или для управления другими устройствами.
Генератор сигналов на базе колебательного контура
Генератор сигналов на базе колебательного контура – это устройство, которое использует колебательный контур для создания стабильного и точного сигнала определенной частоты. Он состоит из колебательного контура, усилителя и обратной связи.
Когда колебательный контур находится в резонансе, он начинает колебаться с определенной частотой. Усилитель усиливает колебания и поддерживает их на постоянном уровне. Обратная связь через колебательный контур помогает стабилизировать частоту и амплитуду сигнала.
Генераторы сигналов на базе колебательного контура широко используются в различных областях, таких как измерения, тестирование, связь и другие. Они обеспечивают стабильные и точные сигналы, которые необходимы для многих приложений.




