Конденсатором называют любые два проводника, разделённые диэлектрическим слоем. Такие проводники должны обладать зарядами одинаковыми по величине, но противоположными по знаку.
Возникающее электрическое поле будет полностью расположено внутри, между проводниками. По этой причине на электрическую ёмкость конденсатора не влияет его внешнее окружение. А на разность потенциалов между пластинами не влияет величина заряда.
Выражение для электроёмкости выглядит так:
Величины $ <phi_1-phi_2=U>$ определяют разность потенциалов, которая также носит название «напряжение» и обозначается «U». Как следует из определения, ёмкость — положительная величина. Её размер определяется габаритами пластин конденсатора, их взаимным расположением, типом диэлектрика. Форма пластин, конструкция конденсатора создаются таким образом, чтобы максимально снизить влияние на внутреннее поле со стороны любых внешних сил или полей. Электрическое поле конденсатора начинается на обкладке с зарядом «+» и заканчивается на обкладке со знаком «-». Ёмкость конденсаторов измеряют так же, как и ёмкость проводников, в международной системе СИ для этого используют Фарады (Ф). Один Фарад — ёмкость конденсатора, где при заряде 1 Кельвин, разность потенциалов 1 Вольт.
Существуют три основных типа конденсаторов: плоские, сферические, цилиндрические. Вычислить ёмкость можно, если найти напряжение на обкладках и определить величину заряда.
Плоские конденсаторы
Плоский конденсатор — элемент состоящий из двух или нескольких плоских пластин, расположенных друг напротив друга, имеющих одинаковый по величине, но разный по знаку заряд. Чтобы не возникало воздушного разряда, пластины разделяют слоем диэлектрика.
Для вычисления ёмкости плоского конденсатора используется выражение:
Здесь S — площадь пластин, чем она больше, тем выше ёмкость. Величина зазора между пластинами — d. Чем меньше d, тем больше ёмкость. Диэлектрическая проницаемость — ε. Она также оказывает значительное влияние на величину ёмкости.
Возьмём конденсатор состоящий из двух пластин, между которыми воздух, и определим его ёмкость. Затем поместим между пластинами диэлектрик, параметр ε которого выше, чем у воздуха. Измерения показывают, что ёмкость конденсатора увеличивается существенно, прямо пропорционально повышению диэлектрической проницаемости.
Чаще всего, при создании плоских конденсаторов делают не две пластины, а «пакет» обкладок в несколько слоёв. Электрическая ёмкость такого элемента, имеющего n слоёв, вычисляется с учётом толщины каждого i-го слоя $d_i$, а также диэлектрической проницаемости каждого слоя $ε_i$.
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
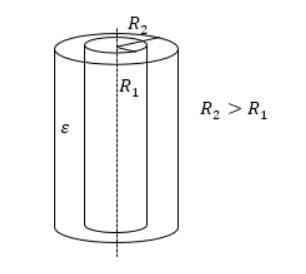
C = 2 πεε 0 l ln R 2 R 1 , где l — высота цилиндров, R 1 и R 2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .
ТОЭ. Расчет цепи с конденсаторами. Найти общую емкость цепи, напряжение и заряд каждого конденсатора
Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.
U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i — это емкость конденсатора с номером i :
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
ε = 1 , ε 0 = 8 , 85 · 10 — 12 Ф м ; S = 1 с м 2 = 10 — 4 м 2 ; d = 1 м м = 10 — 3 м .
Подставим числовые выражения и вычислим:
C = 8 , 85 · 10 — 12 · 10 — 4 10 — 3 = 8 , 85 · 10 — 13 ( Ф ) .
Ответ: C ≈ 0 , 9 п Ф .
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 — 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 — 2 м , внешнем – R 2 = 3 с м = 3 · 10 — 2 м . Значение напряжения — 10 3 В .
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x — расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
Для сферического конденсатора предусмотрена формула вида
C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 с радиусами обкладок R 1 и R 2 .
Производим подстановку выражений для получения искомой напряженности:
E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 — R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 — R 1 .
Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:
E = 10 3 ( 1 + 1 ) 2 · 10 — 4 · 10 — 2 · 3 · 10 — 2 3 · 10 — 2 — 10 — 2 = 3 · 10 — 1 8 · 10 — 6 = 3 , 45 · 10 4 В м .
Ответ: E = 3 , 45 · 10 4 В м .
Батареи конденсаторов
При использовании конденсаторов, их иногда соединяют в батареи. При параллельном соединении n конденсаторов, напряжения U на них одинаковы, а полный заряд q батареи равен сумме зарядов конденсаторов qi, для каждого из которых, очевидно, справедливо (q_ = C_U) .
Рассматривая батарею как один конденсатор, получаем q = CU, другой стороны q = q1 + q2+ … + qn = (C1 + C2 + … + Cn)U.
Получаем, что емкость батареи параллельно соединенных конденсаторов равна сумме емкостей этих конденсаторов: C = C1 + C2 + … + Cn.
Аналогично рассуждая для последовательного соединения конденсаторов, получаем, что емкость такой батареи конденсаторов можно посчитать по формуле:
При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.
Поле вне и внутри конденсатора. Электрическое поле плоского конденсатора в основном локализовано между пластинами и вне конденсатора равно нулю. Поле внутри конденсатора можно выразить через напряжение следующим образом:
Энергия плоского конденсатора. Заряженный конденсатор обладает энергией, которая выражается следующим образом через C, q и U:
Очень важно понимать, какую из формул удобнее применять в каждой конкретной задаче. Например, если в задаче изменяется заряда конденсатора, то следует применять формулу (W = frac>) , если же изменяется заряд, то
Энергетические превращения в конденсаторах
Рассмотрим плоский конденсатор с воздушным зазором, подсоединенный к источнику постоянного напряжения U0. Будем раздвигать пластины конденсатора от расстояния d1 до расстояния d2 в двух случаях: предварительно отсоединив конденсатор от источника питания и не отсоединяя конденсатор от источника питания.
В первом случае, заряд на обкладках конденсатора все время остается неизменным q = CU = const, хотя емкость и напряжение изменяются при движении пластин. Зная напряжение на конденсаторе в начальный момент, находим величину этого заряда (q = C_U_ = frac<varepsilon_S>U_) . Посмотрим, как изменится энергия конденсатора в этом случае. Поскольку заряд конденсатора остается неизменным, применим формулу (W = frac>) и получим:
Во втором случае, когда конденсатор подсоединен к источнику питания, сохраняться будет напряжение, и изменение энергии конденсатора можно рассчитывать по следующей формуле:
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равна:
где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).
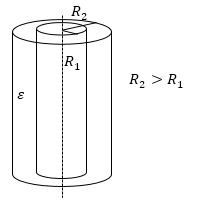
Еще одной, но не маловажной характеристикой всех конденсаторов является пробивное напряжение ($U_$)— это напряжение, при котором происходит электрический разряд через слой диэлектрика. $U_$ зависит от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Помимо одиночных конденсаторов применяют их соединения. Для того чтобы увеличить емкость используют параллельное соединение конденсаторов (соединение одноименными обкладками). В этом случае результирующая емкость такого соединения может быть найдена как сумма
i$ где $С_i$ — емкость конденсатора с номером i:
Если конденсаторы соединить последовательно (обкладками с разными знаками заряда), то суммарная емкость соединения будет всегда меньше, чем минимальная емкость любого конденсатора, который входит в систему. В этом случаем для того чтобы рассчитать результирующую емкость складывают величины, обратные к емкостям отдельных конденсаторов:
Получи помощь с рефератом от ИИ-шки
ИИ ответит за 2 минуты
Задание: Вычислите электроемкость плоского конденсатора, если площадь обкладок его равна 1см2, расстояние между обкладками равно 1 мм. Пространство между обкладками вакуумировано.
Формула для расчета емкости, данного в задаче конденсатора имеет вид:
Ответ: С $approx ,9 пФ.
Задание: Какова напряженность электростатического поля сферического конденсатора на расстоянии x=1 см=$^м$ от поверхности внутренней обкладки, если внутренний радиус обкладки конденсатора $R_1=$1 см$^м$, внешний $R_2=$ 3 см=$^м$. Напряжение на обкладках равно $^3В$.
Напряженность поля, которое создается проводящей заряженной сферой, вычисляется в соответствии с формулой:
где $q$ — заряд внутренней сферы (обкладки конденсатора), $r=R_1+x$ —расстояние от центра сферы.
Заряд сферы найдем из определения емкости конденсатора (С):
Емкость сферического конденсатора определяется как:
где $R_1_2$ — радиусы обкладок конденсатора.
Подставим выражения (2.2) и (2.3) в (2.1), получим искомую напряженность:
Так как все данные в задаче уже переведены в систему СИ, проведем вычисления:
Конденсатор сферический
Данный конденсатор состоит из сплошного или полого сферического проводника, окруженного другой полой концентрической сферической формой другого радиуса.
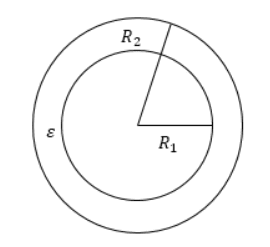
Формула для определения емкости сферического конденсатора
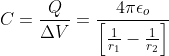
r 1 = внутренний радиус
r 2 = внешний радиус
ε 0 = диэлектрический потенциал (8,85 x 10-12 Ф / м)
Значение емкости двух разных конденсаторов может быть одинаковым, а номинальное напряжение двух конденсаторов может быть разным. Возьмем два конденсатора — один с малым номинальным напряжением, а другой с высоким. Если мы заменим конденсатор с меньшим номинальным напряжением на конденсатор с более высоким номинальным напряжением, то получится конденсатор меньшего размера. Это может произойти из-за неожиданного повышения напряжения.
Нет времени решать самому?
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
- ε 0 — диэлектрическая постоянная, равная 8,85∙10 –12 Кл 2 /(Н∙м 2 );
- ε — диэлектрическая проницаемость среды;
- S (м 2 ) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
W э = q 2 2 C . . = C U 2 2 .
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
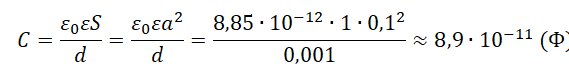
Как устроен конденсатор и от чего зависит его ёмкость?
Конденсатор – это пассивный электронный компонент, способный накапливать заряд и энергию электрического поля, а затем передавать её связанным с ним компонентам цепи. Сходную функцию выполняет и аккумуляторная батарея, однако, в отличие от аккумулятора, весь заряд конденсатор «умеет» накапливать и отдавать практически моментально.
Способность конденсатора накапливать определённое количество заряда определяет его ёмкость, которая в системе СИ измеряется в фарадах и равна отношению накопленного заряда к разности потенциалов между обкладками:
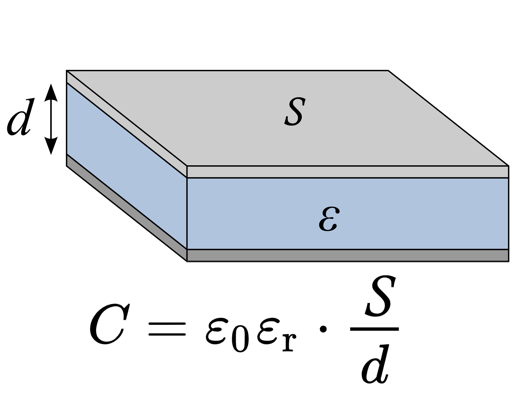
Одной из простейших разновидностей конденсатора является конструкция, состоящая из двух электродов в форме пластин (обкладок), разделённых слоем диэлектрика. В формуле, приведённой на рисунке: S – это площадь обкладок, d – расстояние между ними, εr – диэлектрическая проницаемость диэлектрика, ε0 = 8,854*10 -12 (Ф/м) – электрическая постоянная.
Рис.1 Простейший конденсатор из 2 пластин
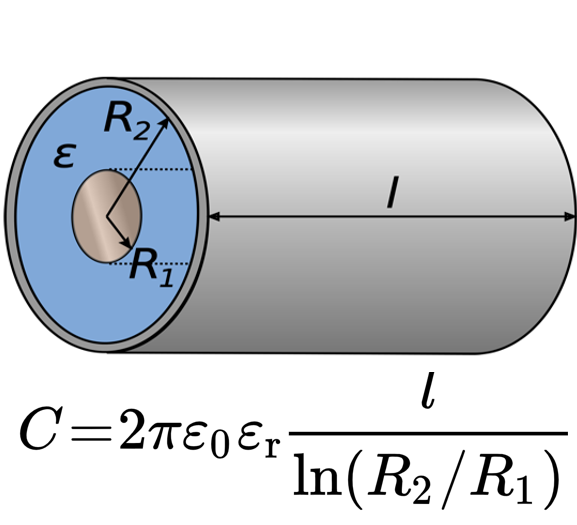
Помимо плоских обкладок, простейший конденсатор может иметь и цилиндрическую форму. Такой конденсатор состоит из двух полых цилиндров, вставленных друг в друга и разделённых слоем диэлектрика.
В формуле: R1 – это радиус внутреннего цилиндра, R2 – радиус внешнего цилиндра, l – длина цилиндров. Точно так же как и в предыдущем случае, εr – это диэлектрическая проницаемость диэлектрика, ε0 = 8,854*10 -12 (Ф/м) – электрич. постоянная.
Рис.2 Простейший цилиндрический конденсатор
Снабдим обе приведённые формулы незамысловатыми онлайн калькуляторами, но прежде сведём в таблицу значения диэлектрической проницаемости некоторых материалов, которые могут пригодиться при изготовлении таких простейших самодельных конденсаторов.
Относительные диэлектрические проницаемости веществ.
| Вещество | ε r | Вещество | ε r | Вещество | ε r |
| Вакуум | 1 | Воздух | 1,0006 | Бумага | 3. 7 |
| Парафин | 2 | Слюда | 6 | Стекло | 4. 10 |
| Текстолит | 5. 7 | Гетинакс | 5. 6 | Каучук | 2,4 |
| Оргстекло | 3,4. 3,5 | Полистирол | 2,4. 2,6 | Полихлорвинил | 3 |
| Полиэтилен | 2,3. 2,4 | Эбонит | 2,5. 3 | Масло трансф. | 2,2 |
А теперь можно переходить к калькулятору:
Расчёт ёмкостей конденсаторов из двух пластин или цилиндров
В промышленном производстве для увеличения ёмкости конденсаторов в основном используется несколько слоёв диэлектрика и электродов, причём это может быть как плоский набор чередующихся прослоек, так и ленты из сменяющихся диэлектриков и электродов, свёрнутые в цилиндр (Рис.1).
Рис.3 Возможные варианты конструкции конденсаторов
Как и любой электронный компонент, конденсатор далеко не идеален и проявляется это в том, что реальные элементы, помимо ёмкости, обладают ещё и собственной паразитной индуктивностью, а также не менее паразитными последовательным и параллельным сопротивлениями. Эквивалентная схема реального конденсатора приведена на Рис.4
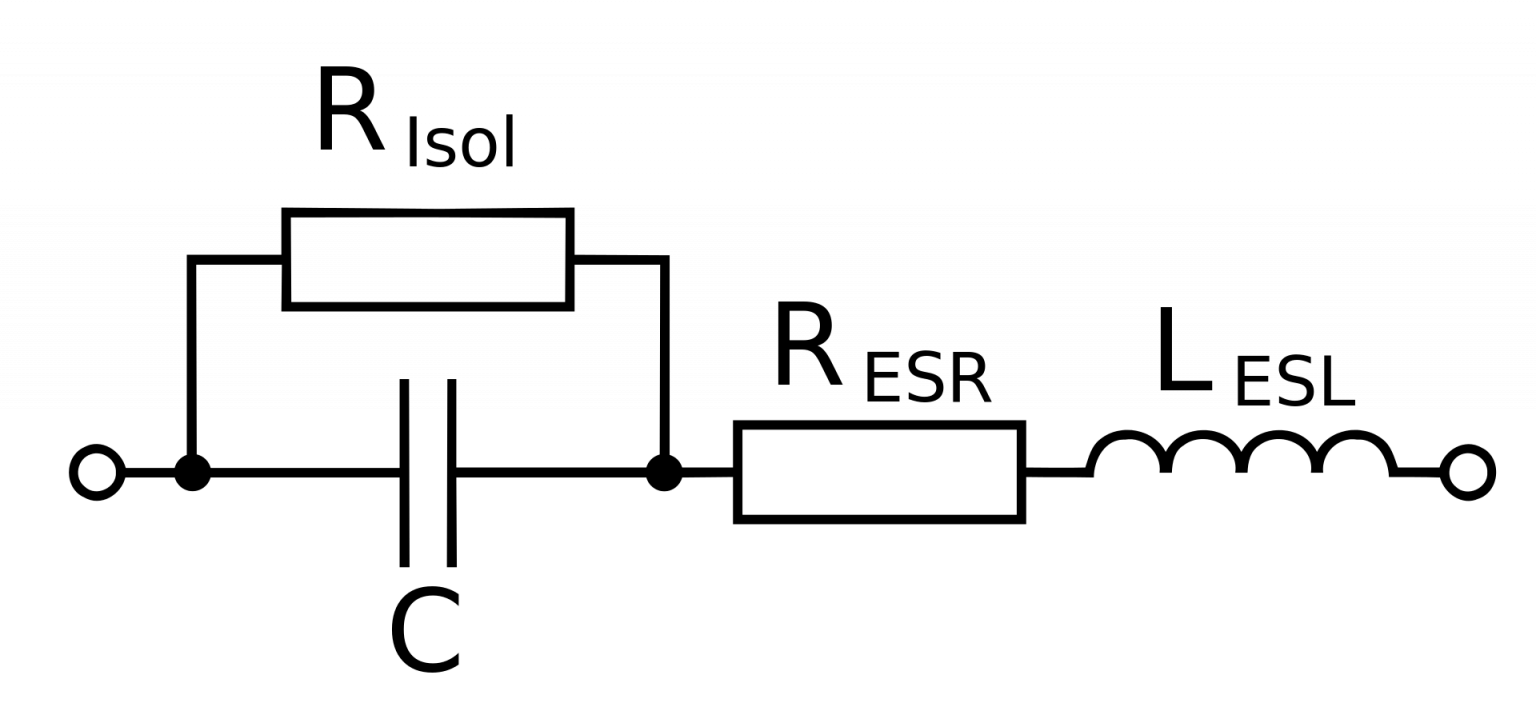
Здесь: C – собственная ёмкость;
Risol – сопротивление изоляции;
Resr – эквивалентное последовательное сопротивление;
Lesl – эквивалентная последовательная индуктивность.
Рис.4 Эквивалентная схема реального конденсатора
Все эти дополнительные элементы, изображённые на схеме, определяют важные характеристики конденсаторов, а конкретно:
Risol – ток утечки и время саморазряда, Resr – тангенс угла диэлектрических потерь и добротность,
Lesl – частоту собственного резонанса конденсатора.
Также к важным параметрам конденсатора следует отнести и температурный коэффициент ёмкости – , который характеризует относительное изменение
ёмкости при изменении температуры окружающей среды на один градус Цельсия.
 |  |
Как устроен конденсатор и от чего зависит его ёмкость?
Конструкция, свойства, формулы, а также основные параметры конденсаторов. Калькулятор расчёта плоских (из двух пластин) и цилиндрических конденсаторов
Конденсатор – это пассивный электронный компонент, способный накапливать заряд и энергию электрического поля, а затем передавать её связанным с ним компонентам цепи. Сходную функцию выполняет и аккумуляторная батарея, однако, в отличие от аккумулятора, весь заряд конденсатор «умеет» накапливать и отдавать практически моментально.
Способность конденсатора накапливать определённое количество заряда определяет его ёмкость, которая в системе СИ измеряется в фарадах и равна отношению накопленного заряда к разности потенциалов между обкладками:

Одной из простейших разновидностей конденсатора является конструкция, состоящая из двух электродов в форме пластин (обкладок), разделённых слоем диэлектрика. В формуле, приведённой на рисунке: S – это площадь обкладок, d – расстояние между ними, εr – диэлектрическая проницаемость диэлектрика, ε0 = 8,854*10 -12 (Ф/м) – электрическая постоянная.
Рис.1 Простейший конденсатор из 2 пластин

Помимо плоских обкладок, простейший конденсатор может иметь и цилиндрическую форму. Такой конденсатор состоит из двух полых цилиндров, вставленных друг в друга и разделённых слоем диэлектрика.
В формуле: R1 – это радиус внутреннего цилиндра, R2 – радиус внешнего цилиндра, l – длина цилиндров. Точно так же как и в предыдущем случае, εr – это диэлектрическая проницаемость диэлектрика, ε0 = 8,854*10 -12 (Ф/м) – электрич. постоянная.
Рис.2 Простейший цилиндрический конденсатор
Снабдим обе приведённые формулы незамысловатыми онлайн калькуляторами, но прежде сведём в таблицу значения диэлектрической проницаемости некоторых материалов, которые могут пригодиться при изготовлении таких простейших самодельных конденсаторов.
Относительные диэлектрические проницаемости веществ.
| Вещество | ε r | Вещество | ε r | Вещество | ε r |
| Вакуум | 1 | Воздух | 1,0006 | Бумага | 3. 7 |
| Парафин | 2 | Слюда | 6 | Стекло | 4. 10 |
| Текстолит | 5. 7 | Гетинакс | 5. 6 | Каучук | 2,4 |
| Оргстекло | 3,4. 3,5 | Полистирол | 2,4. 2,6 | Полихлорвинил | 3 |
| Полиэтилен | 2,3. 2,4 | Эбонит | 2,5. 3 | Масло трансф. | 2,2 |
А теперь можно переходить к калькулятору:
Расчёт ёмкостей конденсаторов из двух пластин или цилиндров
В промышленном производстве для увеличения ёмкости конденсаторов в основном используется несколько слоёв диэлектрика и электродов, причём это может быть как плоский набор чередующихся прослоек, так и ленты из сменяющихся диэлектриков и электродов, свёрнутые в цилиндр (Рис.1).
Рис.3 Возможные варианты конструкции конденсаторов
Как и любой электронный компонент, конденсатор далеко не идеален и проявляется это в том, что реальные элементы, помимо ёмкости, обладают ещё и собственной паразитной индуктивностью, а также не менее паразитными последовательным и параллельным сопротивлениями. Эквивалентная схема реального конденсатора приведена на Рис.4

Здесь: C – собственная ёмкость;
Risol – сопротивление изоляции;
Resr – эквивалентное последовательное сопротивление;
Lesl – эквивалентная последовательная индуктивность.
Рис.4 Эквивалентная схема реального конденсатора
Все эти дополнительные элементы, изображённые на схеме, определяют важные характеристики конденсаторов, а конкретно:
Risol – ток утечки и время саморазряда, Resr – тангенс угла диэлектрических потерь и добротность,
Lesl – частоту собственного резонанса конденсатора.
Также к важным параметрам конденсатора следует отнести и температурный коэффициент ёмкости – , который характеризует относительное изменение
ёмкости при изменении температуры окружающей среды на один градус Цельсия.




