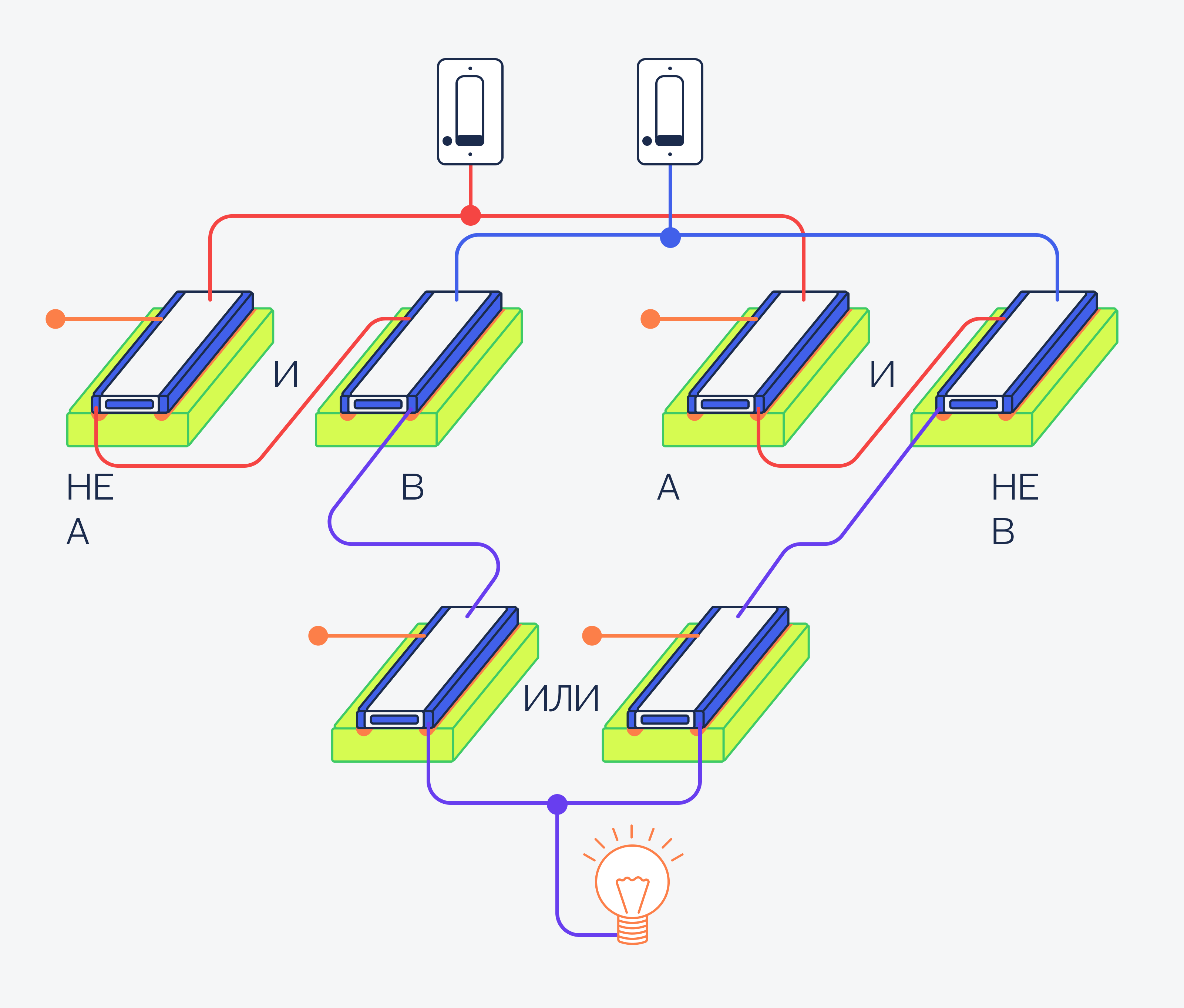
Сколько я себя помню, всегда мечтала сделать процессор. Наконец, вчера я его сделала. Не бог весть что: 8 бит, RISC, текущая рабочая частота — 4 кГц, но он работает. Пока что в программе моделирования логических цепей, но все мы знаем: «сегодня — на модели, завтра — на деле!».
Под катом несколько анимаций, краткое введение в двоичную логику для самых маленьких, короткий рассказ про основные микросхемы логики процессора и, собственно, схема.
Двоичная логика
Двоичная система счисления (для тех, кто не в курсе) — это такая система счисления, в которой нет цифр больше единицы. Такое определение многих сбивает с толку, пока они не вспомнят, что в десятичной системе счисления нет цифр больше девятки.
Двоичная система используется в компьютерах потому, что числа в ней легко кодировать напряжением: есть напряжение — значит, единица; нет напряжения — значит, ноль. Кроме того, «ноль» и «один» легко можно понимать как «ложно» и «истинно». Более того, большая часть устройств, работающих в двоичной системе счисления, обычно относится к числам как к массиву «истинностей» и «ложностей», то есть оперирует с числами как с логическими величинами. Для самых маленьких и тех, кто не в курсе, я расскажу и покажу, как работают простейшие элементы двоичной логики.
Элемент «Буфер»
Представьте, что вы сидите в своей комнате, а ваш друг — на кухне. Вы кричите ему: «Друг, скажи, в коридоре горит свет?». Друг отвечает: «Да, горит!» или «Нет, не горит». Ваш друг — буфер между источником сигнала (лампочкой в коридоре) и приемником (вами). Более того, ваш друг — не какой-нибудь там обычный буфер, а буфер управляемый. Он был бы обычным буфером, если бы постоянно кричал: «Лампочка светится» или «Лампочка не светится».
Элемент «Не» — NOT
А теперь представьте, что ваш друг — шутник, который всегда говорит неправду. И если лампочка в коридоре светится, то он скажет вам «Нет, в коридоре совсем-совсем темно», а если не светится — то «Да, в коридоре свет горит». Если у вас есть такой друг на самом деле, значит, он воплощение элемента «Не».
Элемент «Или» — OR
Для объяснения сути элемента «Или» одной лампочки и одного друга, к сожалению, не хватит. Нужно две лампочки. Итак, у вас в коридоре две лампочки — торшер, к примеру, и люстра. Вы кричите: «Друг, скажи, хотя бы одна лампочка в коридоре светит?», и ваш друг отвечает «Да» или «Нет». Очевидно, что для ответа «Нет» все лампочки обязательно должны быть выключены.
Элемент «И» — AND
Та же самая квартира, вы, друг на кухне, торшер и люстра в коридоре. На ваш вопрос «В коридоре обе лампочки горят?» вы получаете ответ «Да» или «Нет». Поздравляю, теперь ваш друг — это элемент «И».
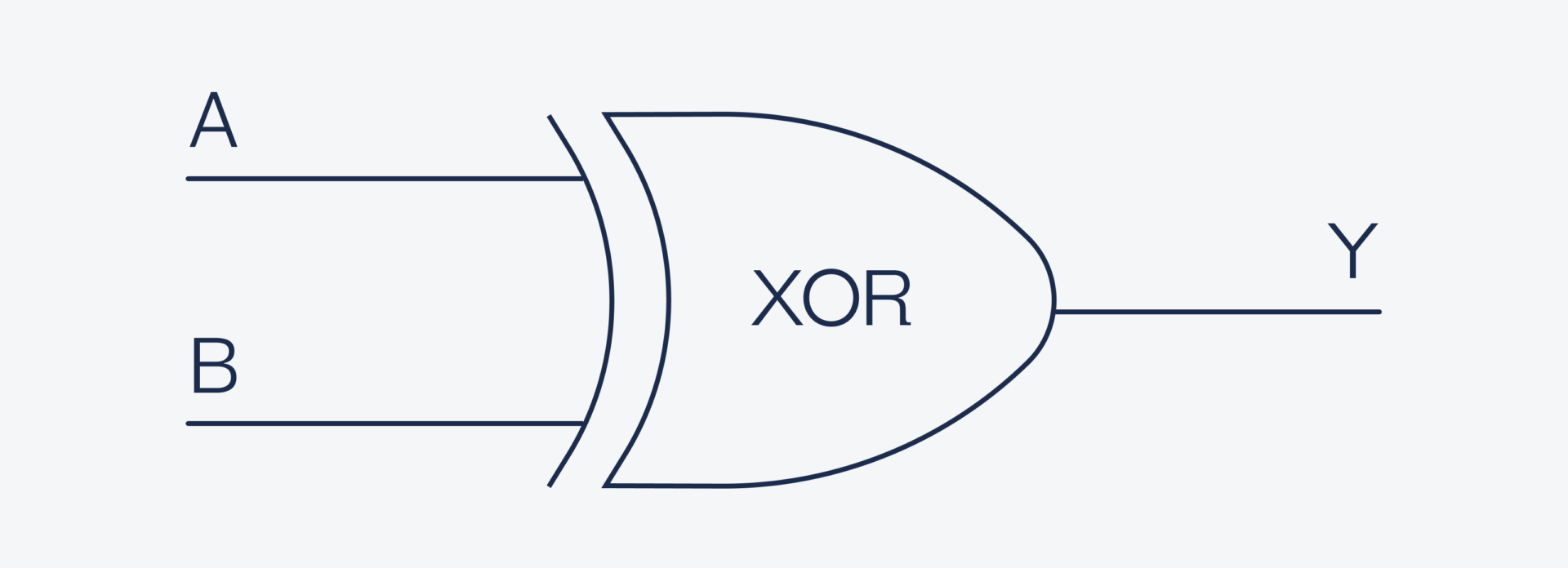
Элемент «Исключающее Или» — XOR
Повторим еще раз эксперимент для элемента «Или», но переформулируем свой вопрос к другу: «Друг, скажи, в коридоре только одна лампочка светит?». Честный друг ответит на такой вопрос «Да» только в том случае, если в коридоре действительно горит только одна лампочка.
Вентиль Исключающее ИЛИ (XOR) — объяснение принципа работы и пример на макетной плате
Применение элемента Исключающее ИЛИ
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию суммирования по модулю 2. Поэтому эти элементы иногда называют сумматорами по модулю два. Основное предназначение элементов Исключающее ИЛИ состоит в сравнении двух входных сигналов (когда на входы приходят два высоких или два низких логических уровня на выходе формируется лог. 0), очень часто данный элемент применяют для формирования задержки сигнала или формирования коротких импульсов.
Важное применение элементов Исключающее ИЛИ – управляемый инвертор. Опишем его работу. Один из входов используется как управляющий, а на другой поступает сигнал. Если на управляющем входе высокий логический уровень, то сигнал инвертируется, а если низкий, то не инвертируется. Чаще всего управляющий сигнал задаётся постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
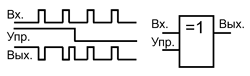
Элемент Исключающее ИЛИ в качестве управляемого инвертора.
Смешивание сигналов
В случае, когда имеется два сигнала и исключается их одновременный приход на элемент Исключающее ИЛИ, то он может быть использован для смешивания сигналов. Такое применение данного элемента может быть использовано в тех случаюх, когда остаются неиспользованными некоторые элементы Исключающее ИЛИ.
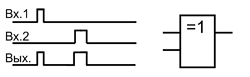
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов.
Более сложные логические элементы
Аннотация: В лекции рассказывается о принципах работы, характеристиках и типовых схемах включения логических элементов, выполняющих сравнительно сложные функции – элементов Исключающее ИЛИ, И-ИЛИ-НЕ, триггеров Шмитта, а также приводятся схемотехнические решения, позволяющие реализовать на их основе часто встречающиеся функции.
Элементы Исключающее ИЛИ ( по -английски — Exclusive-OR) также можно было бы отнести к простейшим элементам, но функция , выполняемая ими, несколько сложнее, чем в случае элемента И или элемента ИЛИ. Все входы элементов Исключающее ИЛИ равноправны, однако ни один из входов не может заблокировать другие входы, установив выходной сигнал в уровень единицы или нуля.
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Рис. 4.1. Обозначения элементов Исключающее ИЛИ: зарубежные (слева) и отечественные (справа)
Под функцией Исключающее ИЛИ понимается следующее: единица на выходе появляется тогда, когда только на одном входе присутствует единица . Если единиц на входах две или больше, или если на всех входах нули, то на выходе будет нуль. Таблица истинности двухвходового элемента Исключающее ИЛИ приведена в табл. 4.1. Обозначения, принятые в отечественных и зарубежных схемах, показаны на рис. 4.1. Надпись на отечественном обозначении элемента Исключающее ИЛИ «=1» как раз и обозначает, что выделяется ситуация, когда на входах одна и только одна единица .
Элементов Исключающее ИЛИ в стандартных сериях немного. Отечественные серии предлагают микросхемы ЛП5 (четыре двухвходовых элемента с выходом 2С), ЛЛ3 и ЛП12, отличающиеся от ЛП5 выходом ОК. Слишком уж специфическая функция реализуется этими элементами.
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию так называемого суммирования по модулю 2. Поэтому эти элементы также называются сумматорами по модулю два. Как уже отмечалось в предыдущей лекции, обозначается суммирование по модулю 2 знаком плюса, заключенного в кружок.
Основное применение элементов Исключающее ИЛИ, прямо следующее из таблицы истинности , состоит в сравнении двух входных сигналов. В случае, когда на входы приходят две единицы или два нуля (сигналы совпадают), на выходе формируется нуль (см. табл. 4.1). Обычно при таком применении на один вход элемента подается постоянный уровень, с которым сравнивается изменяющийся во времени сигнал, приходящий на другой вход. Но значительно чаще для сравнения сигналов и кодов применяются специальные микросхемы компараторов кодов , которые будут рассмотрены в следующей лекции.
В качестве сумматора по модулю 2 элемент Исключающее ИЛИ используется также в параллельных и последовательных делителях по модулю 2, служащих для вычисления циклических контрольных сумм. Но подробно эти схемы будут рассмотрены в лекциях 14,15.
Важное применение элементов Исключающее ИЛИ — это управляемый инвертор (рис. 4.2). В этом случае один из входов элемента используется в качестве управляющего, а на другой вход элемента поступает информационный сигнал. Если на управляющем входе единица , то входной сигнал инвертируется, если же нуль — не инвертируется. Чаще всего управляющий сигнал задается постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала .
Рис. 4.2. Элемент Исключающее ИЛИ как управляемый инвертор
В случае, когда имеется два сигнала одинаковой полярности (положительные или отрицательные), и при этом их одновременный приход исключается, элемент Исключающее ИЛИ может быть использован для смешивания этих сигналов (рис. 4.3). При любой полярности входных сигналов выходные сигналы элемента будут положительными. При положительных входных сигналах элемент Исключающее ИЛИ будет работать как элемент 2ИЛИ, а при отрицательных он будет заменять элемент 2И-НЕ. Такие замены могут быть полезны в тех случаях, когда в схеме остаются неиспользованными некоторые элементы Исключающее ИЛИ. Правда, при этом надо учитывать, что задержка распространения сигнала в элементе Исключающее ИЛИ обычно несколько больше (примерно в 1,5 раза), чем задержка в простейших элементах И, И-НЕ, ИЛИ, ИЛИ-НЕ.
Рис. 4.3. Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов
Рис. 4.4. Выделение фронтов входного сигнала с помощью элемента Исключающее ИЛИ
Еще одно важнейшее применение элемента Исключающее ИЛИ — формирование коротких импульсов по любому фронту входного сигнала (рис. 4.4). В данном случае не важно, положительный фронт входного сигнала или отрицательный, на выходе все равно формируется положительный импульс. Входной сигнал задерживается с помощью конденсатора или цепочки элементов, а затем исходный сигнал и его задержанная копия поступают на входы элемента Исключающее ИЛИ. В обеих схемах в качестве элементов задержки используются также двувходовые элементы Исключающее ИЛИ в неинвертирующем включении (на неиспользуемый вход подается нуль). В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
Данную особенность элементов Исключающее ИЛИ надо учитывать в том случае, когда на оба входа элемента поступают изменяющиеся одновременно сигналы. При этом на выходе элемента возможно появление коротких паразитных импульсов по любому из фронтов входных сигналов. Исключить их влияние на дальнейшую схему можно, например, с помощью синхронизации, подобной рассмотренной в предыдущем разделе.
Логическая операция XOR (исключающее ИЛИ)
Оператор XOR обозначается ^ .
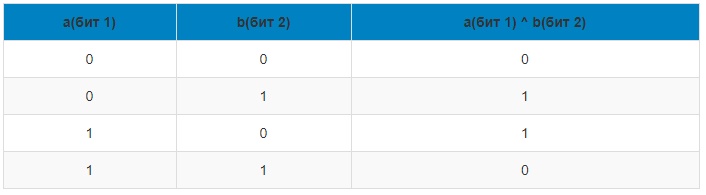
XOR выполняется с 2-мя битами (a и b). Результат выполнения операции XOR (исключающее ИЛИ) равен 1, когда один из битов b или a равен 1. В остальных ситуациях результат применения оператора XOR равен 0.
Таблица истинности логической операции для XOR (исключающее ИЛИ) выглядит так:
Используя XOR (исключающее ИЛИ), вы можете поменять значения 2-х переменных одинакового типа данных, не используя временную переменную. А ещё, посредством XOR можно зашифровать текст, например:
String msg = «This is a message»; char[] message = msg.toCharArray(); String key = «.*)»; String encryptedString = new String(); for(int i = 0; i
Согласен, XOR — далеко не самый надёжный метод шифрования, но это не значит, что его нельзя сделать частью какого-либо шифровального алгоритма.
Логическая операция NOT (НЕ)
Это побитовое отрицание, поэтому выполняется с одним битом и обозначается ~ .
Результат зависит от состояния бита. Если он в нулевом состоянии, то итог операции — единица и наоборот. Всё предельно просто.

Эти 4 логические операции следует запомнить в первую очередь, т. к. с их помощью можно получить практически любой возможный результат. Также существуют такие операции, как > (побитовый сдвиг вправо).
Логические элементы и таблицы истинности
Абсолютно все цифровые микросхемы состоят из одних и тех же логических элементов – «кирпичиков» любого цифрового узла. Вот о них мы и поговорим сейчас. Логический элемент – это такая схемка, у которой несколько входов и один выход. Каждому состоянию сигналов на входах, соответствует определенный сигнал на выходе. Итак, какие бывают элементы? Элемент «И» (AND) Иначе его называют «конъюнктор». Для того, чтобы понять как он работает, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем. Вот так выглядит элемент «И» и его таблица истинности:
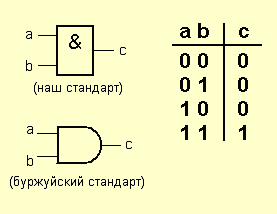
Поскольку вам придется общаться как с русской, так и с буржуйской тех. документацией, я буду приводить условные графические обозначения (УГО) элементов и по нашим и по не нашим стандартам. Смотрим таблицу истинности, и проясняем в мозгу принцип. Понять его не сложно: единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе. Если посмотреть чуток иначе, то можно сказать так: на выходе элемента «И» будет ноль в том случае, если хотя бы на один из его входов подан ноль. Запоминаем. Идем дальше. Элемент «ИЛИ» (OR) По другому, его зовут «дизъюнктор». Любуемся:
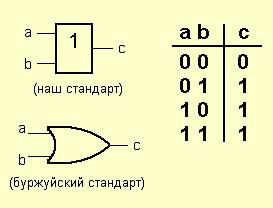
Опять же, название говорит само за себя. На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица. Этот элемент можно назвать также элементом «И» для негативной логики: ноль на его выходе бывает только в том случае, если и на один и на второй вход поданы нули. Едем дальше. Дальше у нас очень простенький, но очень необходимый элемент. Элемент «НЕ» (NOT) Чаще, его называют «инвертор».
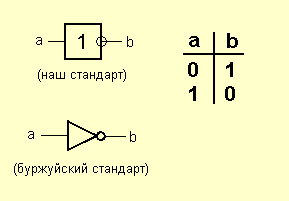
Надо чего-нибудь говорить по поводу его работы? Ну тогда поехали дальше. Следующие два элемента получаются путем установки инвертора на выход элементов «И» и «ИЛИ». Элемент «И-НЕ» (NAND)
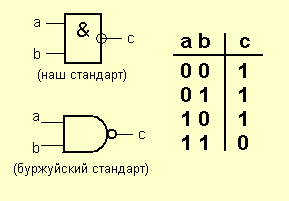
Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» — единица. И наоборот. Э то легко понять по эквивалентной схеме элемента:
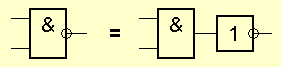
Элемент «ИЛИ-НЕ» (NOR)
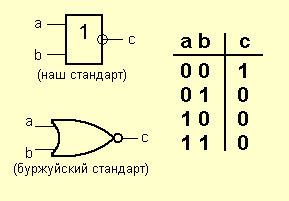
Та же история – элемент «ИЛИ» с инвертором на выходе. Следующий товарищ устроен несколько хитрее:
Элемент «Исключающее ИЛИ» (XOR) Он вот такой:
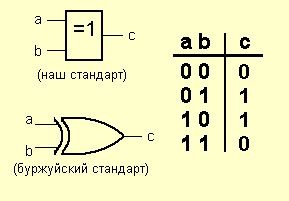
Операция, которую он выполняет, часто называют «сложение по модулю 2». На самом деле, на этих элементах строятся цифровые сумматоры. Смотрим таблицу истинности. Когда на выходе единицы? Правильно: когда на входах разные сигналы. На одном – 1, на другом – 0. Вот такой он хитрый. Эквивалентная схема примерно такая:
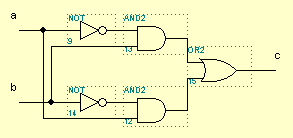
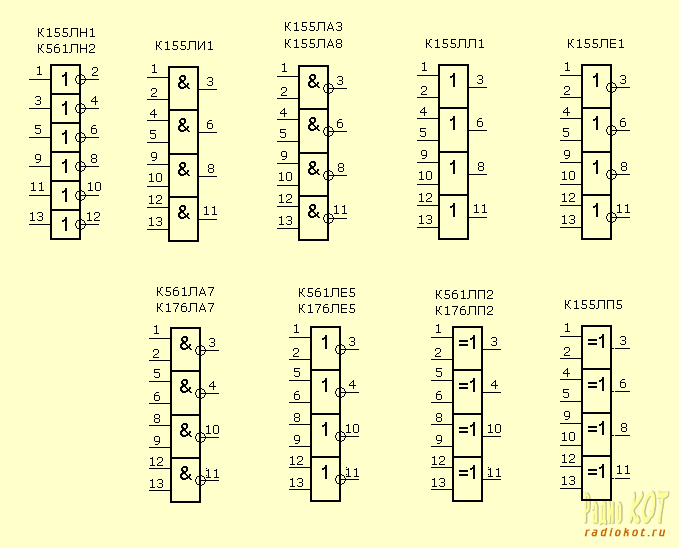
Ее запоминать не обязательно. Собственно, это и есть основные логические элементы. На их основе строятся абсолютно любые цифровые микросхемы. Даже ваш любимый Пентиум 4. Далее мы позанудствуем о том, как синтезировать цифровую схему, имея ее таблицу истинности. Это совсем несложно, а знать надо, ибо пригодится (еще как пригодится) нам в дальнейшем. Ну и напоследок – несколько микросхем, внутри которых содержатся цифровые элементы. Около выводов элементов обозначены номера соответствующих ног микросхемы. Все микросхемы, перечисленные здесь, имеют 14 ног. Питание подается на ножки 7 (-) и 14 (+). Напряжение питания – смотри в таблице в предыдущем параграфе. Источник: radiokot.ru
 none
none  Опубликована: 2005 г.
Опубликована: 2005 г.  0
0  1
1
![]()
 Вознаградить Я собрал 0 0
Вознаградить Я собрал 0 0
Как считают процессоры: короткий рассказ про XOR и транзисторы
В одной из статей мы говорили о транзисторах и о том, как они устроены. Сегодня будет практика — мы соберём из транзисторов XOR и выясним, сколько для этого нужно транзисторов.
Чтобы лучше понять, что будет дальше, напомним, что такое транзистор. Если хотите копнуть поглубже, почитайте наш разбор:
Транзисторы выполняют всю компьютерную работу: считают, запускают программы, управляют датчиками и отвечают за работу устройства в целом.

При этом сам транзистор — простейший прибор, который, по сути, похож на кран или электрические ворота. Через транзистор идёт какой-то один ток, а другим током этот поток можно либо пропустить, либо заблокировать. И всё.
Вот примерная схема. В жизни ножки транзистора могут быть расположены не так, как на схеме, но для наглядности нам надо именно так:
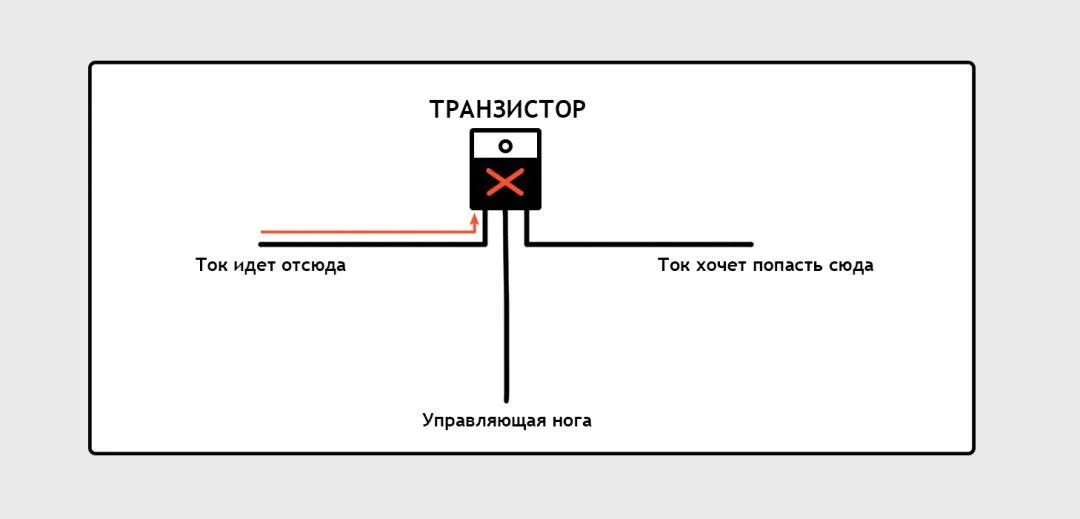
Ток пытается пройти сквозь транзистор, но транзистор «закрыт»: на его управляющую ногу не подан другой ток.
А теперь мы подали на управляющую ногу немного тока, и транзистор «открылся» и пропускает через себя основной ток.
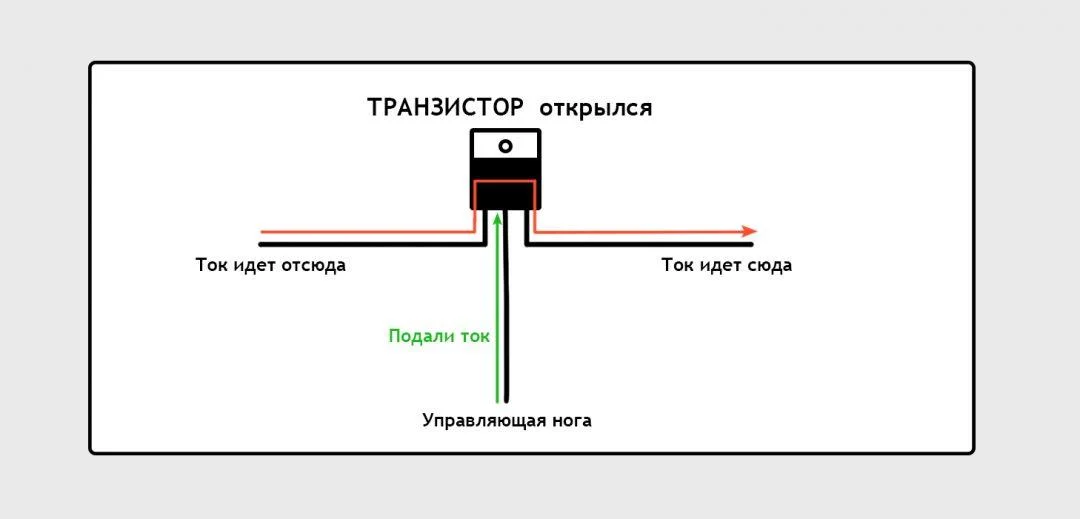
Из миллиардов таких простейших «кранов» и состоит любая современная вычислительная машина: от чайника с электронным управлением до суперкомпьютера в подвалах Пентагона. И до чипа в вашем смартфоне.
Что такое XOR и где это применяется
XOR — исключающее «или». Оно сравнивает два элемента и, если они равны, возвращает 0, а если разные — 1. XOR широко используется в процессорах для выполнения простейших математических операций. Ну и идеологически это основа всей сложной программистской логики: любой оператор сравнения в вашей программе так или иначе будет опираться на работу XOR.
Если мы откроем любой учебник по матлогике, там будет написано, как с помощью И, ИЛИ и НЕ получить XOR. Похоже на сложное нечитаемое заклинание:
(НЕ(a) И b) ИЛИ (а И НЕ(b))
Мы уже знаем, как сделать на транзисторах все эти элементы, поэтому просто соберём их в одно целое.
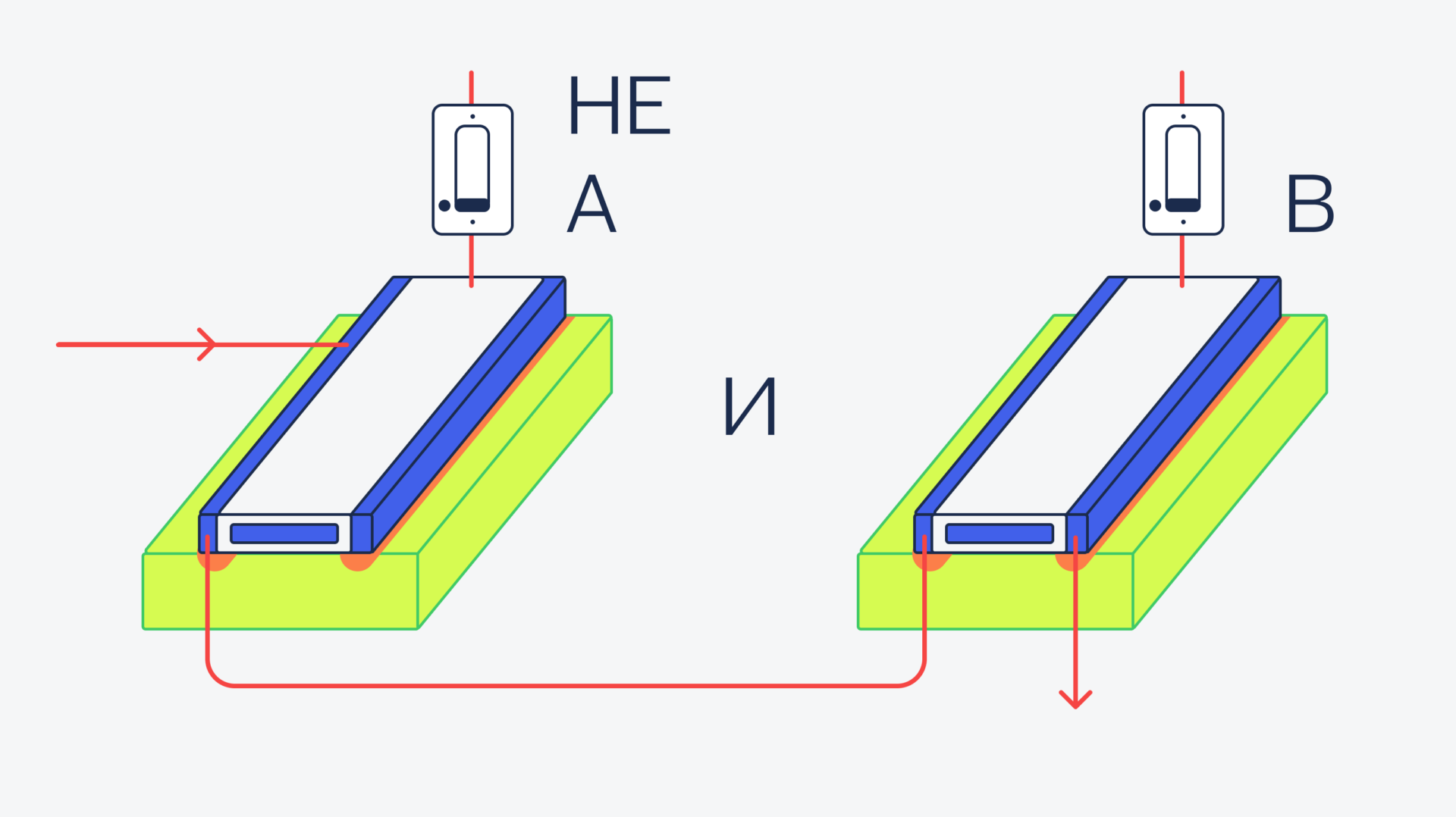
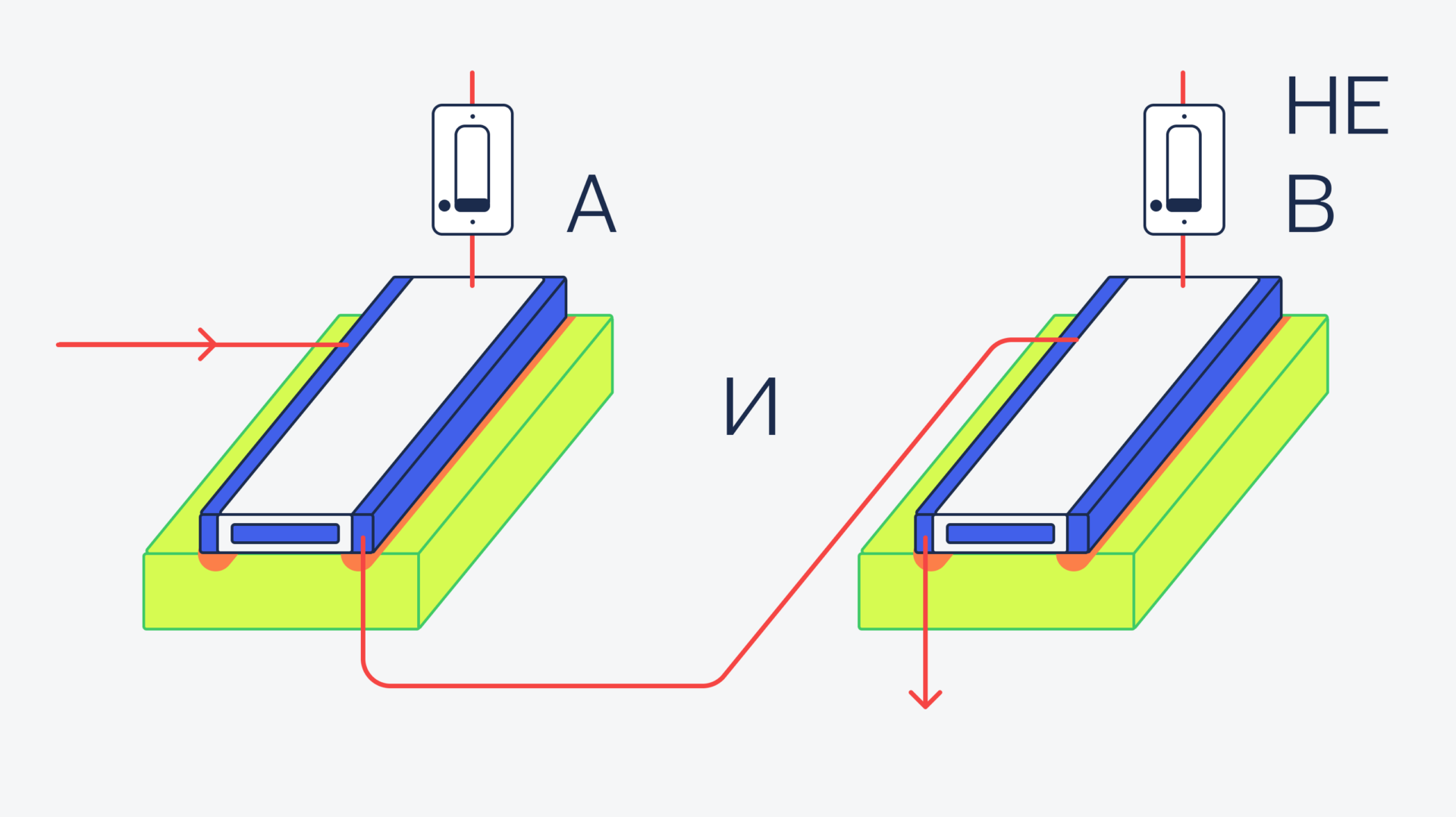
Теперь объединим это в одно целое, используя логическое ИЛИ.
(НЕ(a) И b) ИЛИ (а И НЕ(b)):
На схемах XOR обозначается так:
Выглядит громоздко, но при этом работает как нужно. Целых 6 транзисторов нам понадобилось, чтобы реализовать XOR.
Криптографические алгоритмы

В статье рассматривается реализация наиболее распространенных криптографических алгоритмов. Мы начнем с фундаментальной функции XOR, затем обсудим более сложные симметричные и асимметричные алгоритмы. Статья завершится обзором асимметричного алгоритма для обмена общим закрытым ключом.
Функция XOR
XOR (исключающее ИЛИ) – критически важная логическая операция, используемая во многих, если не во всех, криптографических алгоритмах. На рисунке 1 показано, как работает эта базовая функция. Ее понимание необходимо перед анализом любого из алгоритмов.

Рис. 1. Схема работы функции XOR
Исключающее ИЛИ – основной элемент шифрования без потери данных
Благодаря свойствам XOR один из входов может использоваться в качестве ключа для передачи данных на другой вход. Например, если A – одиночный бит ключа шифрования, XOR с битом данных из B «переключает» бит в другое состояние, если A – 1. Повторное применение побитовой операции XOR с ключом и зашифрованным сообщением расшифровывает его.
Рассмотрим пример. Наша цель – зашифровать слово Secret ключом с помощью XOR, а затем расшифровать его с помощью того же ключа и функции XOR. Это делается следующим образом.
1. Выбираем ключ. В его качестве мы выбираем букву k.

- Преобразуем букву k в двоичный код, используя стандарт кодировки символов ASCII (American Standard Code for Information Interchange). Результат: 01101011.
- Преобразуем слово Secret в двоичный код. Результат: 01010011 01100101 01100011 01110010 01100101 01110100.
- Применяем операцию XOR к каждой букве слова Secret с ключом k. Получаем зашифрованное сообщение:
- Теперь, чтобы расшифровать зашифрованное сообщение, мы применяем к нему XOR с кодом ключа k. Этот шаг возвращает первоначальное слово Secret.

Безопасный алгоритм хэширования SHA
Основное назначение функции SHA (Secure Hash Algorithm) состоит в сжатии данных переменного размера в битовую строку фиксированного размера. Эта операция называется хэшированием.
Функции SHA – это семейство алгоритмов хэширования, разрабатываемых в течение длительного времени под наблюдением американского Национального института стандартов и технологий (NIST). Последним из них является функция SHA-3. На рисунке 2 показана основная концепция безопасной генерации хэша.
Функция SHA имеет следующие характеристики.
- Переменная длина входного текста.
- Фиксированная длина выходного значения.
- Это необратимая функция. Используя алгоритм, описанный на рисунке 2, невозможно использовать полученное хэш-значение для регенерации входного текста, кроме как попробовать каждый возможный входной текст. Для достаточно больших входных данных это становится вычислительно невозможным.
- Если одно и то же входное сообщение подается в функцию SHA, она всегда генерирует один и тот же результирующий хэш.
- Невозможно сгенерировать одно и то же хэш-значение, используя два разных входных значения. Это называется «устойчивостью к коллизиям».
- Небольшое изменение входного значения, даже одного бита, полностью меняет результирующее хэш-значение. Это называется «лавинным эффектом».

Рис. 2. Структурная схема базовой концепции безопасной генерации хэша
Если хэш-функция удовлетворяет всем перечисленным требованиям, она считается сильной хэш-функцией. Некоторые из используемых в настоящее время функций SHA – это SHA-1, SHA-2 и SHA-3.
Теперь давайте рассмотрим, как работают функции SHA. В этой статье мы рассмотрим только SHA-2 и SHA-3. SHA-1 постепенно выводится из применения и не рекомендуется для каких-либо новых устройств.
Как работает SHA-2?
Функция SHA-2 имеет четыре основных типа, различающихся длиной выходного значения:
- SHA-224 – хэш имеет длину 224 бит.
- SHA-256 – хэш имеет длину 256 бит.
- SHA-384 – хэш имеет длину 384 бит.
- SHA-512 – хэш имеет длину 512 бит.
В качестве примера рассмотрим SHA-256. На рисунке 3 показана структурная схема алгоритма SHA-256.

Рис. 3. Безопасная генерация хэша с помощью функции SHA-256
Безопасная генерация хэша: функция SHA-256
Сначала входное сообщение дополняется до целого числа 512-бит блоков. Затем первый 512-бит блок подается в функцию сжатия вместе с начальным 256-бит хэш-значением. По сути, функция сжатия перетасовывает сообщение 64 раза, сжимает его до 256 бит и отправляет в следующий блок сжатия или выдает его как окончательный хэш. Таким образом, изменяемое входное сообщение много раз перетасовывается, предотвращая его использование для получения исходного сообщения. После этого генерируется выходной хэш.
Как работает SHA-3?
Функция SHA-3 не имеет предопределенной длины выходного значения. Длины входных и выходных сообщений также не имеют ограничения максимального размера. Для сравнения с SHA-2 мы определим четыре основных типа с разными длинами выходного значения:
- SHA3-224 – хэш имеет длину 224 бит.
- SHA3-256 – хэш имеет длину 256 бит.
- SHA3-384 – хэш имеет длину 384 бит.
- SHA3-512 – хэш имеет длину 512 бит.
Давайте рассмотрим в качестве примера SHA3-256. SHA-3 использует функцию криптографической губки Keccak. Аналогично губке, на первом шаге входное сообщение «впитывается» или «поглощается». На следующем этапе «выжимается» выходной хэш. На рисунке 4 представлена структурная схема функции SHA3-256.

Рис. 4. Безопасная генерация хэша с помощью функции SHA3-256
Безопасная генерация хэша: функция SHA3-256
Итеративная функция, показанная на рисунке 4, берет 1600 бит данных и затем проводит их через 24 раунда перестановки, используя определенный алгоритм. После этого она переходит к следующему 1600-бит блоку. Это продолжается до тех пор, пока не завершится фаза поглощения.
По ее завершении последний 1600-бит блок передается для сжатия. В этом случае, поскольку длина выходного хэша SHA3-256 не превышает 1088 бит, фаза сжатия не нуждается в каких-либо итеративных функциях. Первые 256 бит с последнего этапа и есть выходной хэш.
Например, если требуемая длина хэша составляет 2500 бит, то чтобы получить хэш нужной длины, понадобились бы еще три вхождения итеративной функции.
AES (усовершенствованный стандарт шифрования)
Как и у более старых алгоритмов шифрования, например DES (стандарт шифрования данных) и 3DES (тройной стандарт шифрования данных), целью алгоритма AES является обратимое скремблирование и замена входных данных на основе значения входного ключа. Результат называется шифротекстом.
Алгоритм AES был разработан для замены уязвимых для атак алгоритмов DES и 3DES, появившихся ранее. На рисунке 5 описан алгоритм AES.

Рис. 5. Краткий обзор алгоритма AES
Алгоритм AES
Алгоритм AES – это алгоритм шифрования фиксированной ширины. Поэтому входное сообщение сначала дополняется так, чтобы оно заняло целое число 128-бит блоков.
Каждый 128-бит блок подается в алгоритм шифрования вместе с ключом шифрования. В зависимости от количества битов в ключе шифрования алгоритм AES выполняет определенное количество раундов сокрытия битов входного блока.
Сокрытие осуществляется с помощью перетасовки битов данных, взятия частей данных и замены их значениями из таблицы поиска (например, шифра Цезаря), а также выполнения операций XOR для переключения битов с 0 на 1 в соответствии со значениями битов в наборе «раундовых ключей», генерируемых из входного ключа шифрования. Раундовый ключ используется один раз для одного из раундов сокрытия и создается «расширением» части ключа шифрования с помощью копирования битов и вставки этих копий между другими битами.
Функция дешифрования AES выполняет обратные операции функции шифрования, используя для расшифровки исходных данных входного блока тот же ключ шифрования.
3DES (тройной стандарт шифрования данных)
Основная идея алгоритма 3DES заключается в обратимом скремблировании и замене входных данных на основе входного ключа. Результат называется шифротекстом.
Алгоритм 3DES основан на алгоритме DES, разработанном в 1970-х гг. Когда в 1990-х гг. DES был скомпрометирован, стала очевидна необходимость в более безопасном алгоритме. 3DES оказался скорейшим решением проблем с DES. Чтобы понять алгоритм 3DES, сначала следует рассмотреть описание оригинального DES, показанного на рисунке 6.

Рис. 6. Обзор алгоритма DES
Алгоритм DES
Поскольку алгоритм DES шифрования имеет фиксированную ширину, входное сообщение сначала дополняется, чтобы оно заняло целое число 64-бит блоков.
Каждый 64-бит блок подается в алгоритм шифрования вместе с 56-бит ключом шифрования (большинство версий алгоритма принимают 64-бит ключ, но 8 бит игнорируются). Функция шифрования использует входной ключ для генерации 16 «подключей», каждый из которых используется для 16 раундов сокрытия битов входного блока. Это сокрытие осуществляется с помощью перетасовки битов данных, взятия частей данных и замены их значениями из таблицы поиска (например, шифра Цезаря), а также выполнения операций XOR для переключения битов с 0 на 1 в соответствии со значениями битов в подключах.
Функция дешифрования DES выполняет обратные операции функции шифрования, используя для расшифровки исходных данных входного блока тот же ключ шифрования.
Посмотрим, как работает 3DES.
Превращение алгоритма DES в 3DES
После открытия уязвимости DES для атак методом «грубой силы» (циклического перебора всех возможных значений ключа до тех пор, пока не обнаружатся исходные блоки сообщений), был разработан простой метод эффективного увеличения размера ключа шифрования. На рисунке 7 представлено решение 3DES.

Рис. 7. Для создания алгоритма 3DES используются три операции DES
Алгоритм 3DES – это в прямом смысле три операции DES. Первая и последняя из них являются операциями шифрования, в то время как средняя представляет собой операцию дешифрования. Заметим, что «шифрование» и «дешифрование» – просто названия, присвоенные операциям скремблирования, которые являются обратными друг другу.
Для каждой операции DES, выполняемой в 3DES, используется соответствующий ключ. Часто для первой и третьей операций применяется один и тот же ключ. Использование одного и того же ключа для первой и третьей операций и другого ключа для средней операции эффективно удваивает общую длину ключа. Это делает атаку «грубой силы» намного сложнее и устраняет уязвимости алгоритма DES.
Система шифрования с открытым ключом RSA
Система RSA, названная в честь своих создателей – Рона Ривеста (Ron Rivest), Ади Шамира (Adi Shamir) и Леонарда Адлемана (Leonard Adleman), является одной из первых асимметричных систем шифрования/дешифрования с открытым ключом. Этот алгоритм использует свойства арифметических операций над абсолютными значениями простых чисел для генерации открытого ключа для шифрования и закрытого ключа для дешифрования. Операции шифрования и дешифрования основаны на этом же принципе. Общее представление об RSA дает рисунок 8.

Рис. 8. Общее представление о шифровании RSA
Операция генерации ключей и шифрования/дешифрования известна как односторонняя функция, или «лазейка». Это математические операции, которые относительно просто вычислить в одном направлении, но трудно в другом. Например, легко выполнить умножение на 2, но труднее вычислить квадратный корень из X.
В случае RSA два больших простых числа умножаются для создания части открытого и закрытого ключей. Умножение – простая операция; разложение на множители для нахождения секретных простых чисел – трудная.
Кроме того, гораздо проще зашифровать сообщение с помощью открытого ключа, чем пытаться действовать в обратном направлении, чтобы узнать сообщение, не имея закрытого ключа. Однако с помощью закрытого ключа можно легко расшифровать сообщение, и потому он никогда не должен стать доступным посторонним лицам. Закрытый ключ можно рассматривать как лазейку, открывающую кратчайший путь для обхода сложного лабиринта попыток взлома зашифрованного сообщения.
Безопасность RSA зависит от больших простых чисел и сложных операций. Даже легкий путь с его функцией «лазейки» с большими ключами для очень многих вычислительных систем является затруднительным. Поэтому RSA часто используется в качестве средства передачи общих ключей шифрования, которые можно использовать в более быстрых симметричных алгоритмах, например DES, 3DES и AES для отдельных транзакций.
Алгоритм ECDSA
Алгоритм цифровой подписи на основе эллиптических кривых (ECDSA) позволяет участнику обмена данными доказать подлинность, генерируя цифровую подпись для входного сообщения на основе скрытой части информации, известной как закрытый ключ. Этот ключ необходим для создания открытого ключа, который применяется другими участниками для проверки подлинности участника.
Цифровые подписи генерируются с помощью входного сообщения, закрытого ключа и случайного числа. Затем открытый ключ можно использовать для проверки того, что владелец подписи (или участник) владеет соответствующим закрытым ключом и потому является подлинным. Эту концепцию иллюстрирует рисунок 9.

Рис. 9. ECDSA позволяет проверять цифровые подписи
Алгоритм цифровой подписи был впервые введен с модульной арифметикой, которая зависит от больших простых чисел и вычислений, требующих большого использования вычислительных мощностей. Криптография с эллиптическими кривыми использует математические свойства эллиптических функций для упрощения математических вычислений без ущерба для безопасности.
Операции генерации и подписания ключей известны как односторонняя функция, или «лазейка». Как и операции RSA, эти вычисления эллиптической кривой относительно просты для вычисления в одном направлении, но для вычисления в другом направлении трудны. Закрытый ключ можно рассматривать как лазейку, открывающую кратчайший путь для обхода сложного лабиринта попыток для взлома генерации и подписания ключей.
ECDSA позволяет одному участнику подписывать сообщения, полученные от любого участника. Однако, чтобы доказать подлинность с помощью ECDSA, подписавший не должен заранее знать о том, что сообщение будет подписано. Это отсутствие контроля над сообщением позволяет другому участнику коммуникации «бросить вызов» подписавшему новой информацией, чтобы доказать владение закрытым ключом.
Протокол обмена ключами ECDH
Протокол обмена ключами Диффи-Хеллмана на эллиптических кривых (ECDH) позволяет двум участникам определить общий ключ для обмена данными; существует только одна часть скрытой информации, называемая закрытым ключом. Без этого ключа одной из вовлеченных сторон перехватчик не сможет легко определить общий ключ. Однако этот алгоритм позволяет объединить закрытый ключ одной стороны и открытый ключ другой стороны для получения результирующего ключа, который является одинаковым для обеих сторон. Эта концепция иллюстрируется рисунком 10.

Рис. 10. Протокол обмена ключами ECDH позволяет двум сторонам установить общий ключ для передачи данных
Обмен ключами ECDH
Обмен ключами Диффи-Хеллмана был впервые введен с модульной арифметикой, которая зависит от больших простых чисел и вычислений, требующих большой вычислительной мощности. Криптография с эллиптическими кривыми использует математические свойства эллиптических функций для упрощения математических вычислений без ущерба для безопасности.
Как и ECSDA, операции генерации и комбинации ключей известны как односторонняя функция, или «лазейка». Вычисления эллиптической кривой относительно просты для вычисления в одном направлении, но для вычисления в другом направлении требуют больших затрат. Закрытый ключ можно рассматривать как лазейку, открывающую кратчайший путь для обхода сложного лабиринта попыток для взлома генерации или комбинации ключей.
Алгоритм ECDH позволяет двум сторонам вместе определить ключ, но он не гарантирует, что любой из сторон можно доверять – для этого требуются дополнительные уровни аутентификации. Если открытый ключ получает сертификат, например подпись ECDSA, вычисленную с помощью закрытого ключа от доверенного владельца, то открытый ключ определяется путем проверки подлинности сертификата этого ключа с помощью открытого ключа доверенного владельца, выдавшего сертификат.
Используя открытые ключи с сертификатами от доверенного центра, участники ECDH могут быть уверены, что их коллега является подлинным участником.




