Документ предоставляется как есть, мы не несем ответственности, за правильность представленной в нём информации. Используя информацию для подготовки своей работы необходимо помнить, что текст работы может быть устаревшим, работа может не пройти проверку на заимствования.
Если Вы являетесь автором текста представленного на данной странице и не хотите чтобы он был размешён на нашем сайте напишите об этом перейдя по ссылке: «Правообладателям»
Можно ли скачать документ с работой
Да, скачать документ можно бесплатно, без регистрации перейдя по ссылке:
Лекция 6 АЛУ
Арифметико-логическое устройство (или АЛУ, ALU) предназначено для обработки информации в соответствии с полученной процессором командой. Примерами обработки могут служить логические операции (типа логического «И», «ИЛИ», «Исключающего ИЛИ» и т.д.) то есть побитные операции над операндами, а также арифметические операции (типа сложения, вычитания, умножения, деления и т.д.). Над какими кодами производится операция, куда помещается ее результат — определяется выполняемой командой. Если команда сводится всего лишь к пересылке данных без их обработки, то АЛУ не участвует в ее выполнении.
Быстродействие АЛУ во многом определяет производительность процессора. Причем важна не только частота тактового сигнала, которым тактируется АЛУ, но и количество тактов, необходимое для выполнения той или иной команды. Для повышения производительности разработчики стремятся довести время выполнения команды до одного такта, а также обеспечить работу АЛУ на возможно более высокой частоте. Один из путей решения этой задачи состоит в уменьшении количества выполняемых АЛУ команд, создание процессоров с уменьшенным набором команд (так называемые RISC-процессоры). Другой путь повышения производительности процессора — использование нескольких параллельно работающих АЛУ.
Что касается операций над числами с плавающей точкой и других специальных сложных операций, то в системах на базе первых процессоров их реализовали последовательностью более простых команд, специальными подпрограммами, однако затем были разработаны специальные вычислители — математические сопроцессоры, которые заменяли основной процессор на время выполнения таких команд. В современных микропроцессорах математические сопроцессоры входят в структуру как составная часть.
Рассмотрим для примера следующую схему АЛУ,
которое выполняется в виде самостоятельной БИС либо входит в состав других более сложных ИМС. АЛУ (рис. 1, а) позволяет производить арифметические и логические операции над n-разрядными входными кодами (n обычно 4, 8 или 16); входные коды обозначены А и В. Сигналы, подаваемые на управляющие входы М, S, определяют, какая именно операция может быть выполнена над входными величинами, а также при выполнении арифметических операций на АЛУ может быть подан сигнал переноса из внешней цепи Р0 , который добавляется в младший разряд АЛУ, на выходе АЛУ формируется сигнал Р4, переноса из старшего разряда (сигнал переполнения).
Собираем 8-битное арифметико-логическое устройство (АЛУ)
Сигнал переноса Р увеличивает результат (число F) на единицу. АЛУ представляет собой логическую схему, имеющую определенное количество входов и выходов, где F— результаты операций в каждом разряде, P4— сигнал переноса из старшего разряда.
Рис. 1. Арифметико-логическое устройство (а) и микропроцессор (б) — упрощенная структурная схема
Совокупность сигналов на всех входах однозначно определяет совокупность выходных сигналов.
При управляющем сигнале М=0 АЛУ выполняет арифметические операции над n-разрядными входными двоичными числами А и В:
— арифметическое сложение А и В,
— арифметическое сложение А и В с добавлением единицы в младший разряд из внешней цепи (сигнал Р0),
— арифметическое вычитание В из A,
— арифметическое вычитание B из A с учетом заема единицы из младшего разряда,
— увеличение или уменьшение числа А на единицу,
— пересылка чисел А и В с входа АЛУ на выход,
— сдвиг чисел на один разряд влево (это эквивалентно умножению на два)
— сдвиг чисел на один разряд вправо (эквивалентно делению на два) и др.
Комбинация сигналов S определяет, какая именно математическая операция производится АЛУ.
При М=1 АЛУ выполняет логические операции над функциями A и B (во всех разрядах выполняется одна и та же логическая операция). В табл. 4.16 перечислены 16 логических операций, выполняемых АЛУ в зависимости от управляющих сигналов S.
Логические операции, выполняемые арифметико-логическим устройством (АЛУ)
1.Инверсия входного сигнала А.
2. Инверсия логической суммы входных сигналов (стрелка Пирса).
3. Запрет по А .
4. Нуль на выходе при любых значениях входного сигнала (константа 0).
5. Логическая сумма инверсных значений входных сигналов
6. Инверсия входного сигнала В.
7. Сложение по модулю 2 (исключающее ИЛИ, нечет, неэквивалентность)
8. Запрет по В.
9. Импликация от А к В.
10. Эквивалентность (равнозначность, чет)
11. Передача на выход входного сигнала В.
12. Логическое умножение (конъюнкция, «И»)
13. Единица на выходе при любых значениях входного сигнала (константа 1)
14. Импликация от В к А
15. Логическое сложение (дизъюнкция, «ИЛИ») двух или более логических значений.
16. Передача на выход входного сигнала А
Вопросы к лекции 6 АЛУ.
1. Назначение АЛУ. (стр. 1)
2. Примерами операций выполняемых АЛУ. (стр. 1)
3. Что учитывается при определении быстродействия (производительности) АЛУ? (стр. 1)
4. Пути повышения производительности АЛУ. (стр. 1)
5. Как выполнялись сложные операции, например, над числами с плавающей запятой в первых процессорах. Для чего применялись сопроцессоры? Как решается эта проблема в настоящее время? (стр. 1)
6. Зарисовать предложенную схему АЛУ (стр. 2, рис 1а)
Пояснить назначение всех входных и выходных сигналов. (стр. 1-2).
Над скольки — разрядными числа производятся операции в данном АЛУ?
7. Какие арифметические операции выполняет данное АЛУ при М=0? (стр. 2)
Привести примеры:
А) арифметического сложения чисел А=516 и В=618 без учета входного переноса (Р0 =0)
Б) арифметического сложения чисел А=516 и В=616 с учетом входного переноса (Р0=1)
В) вычитания из В=610 числа А=516.
8. Какие логические операции выполняет данное АЛУ при М=1?
Привести примеры:
А) логического сложения чисел А=516 и В=616
Б) логического умножения чисел А=516 и В= 616
В) сложить по модулю 2 числа А=516 и В= 616
Арифметико-логическое устройство
Арифметико-логическое устройство (АЛУ) является узлом ЭВМ, который выполняет арифметические и логические операции над данными, обрабатываемыми ЭВМ.
В общем случае многофункциональное АЛУ включает операционную часть (ОУ) и устройство управления (УУ), которое осуществляет вторичную дешифрацию кода команды и определяет выполняемую в АЛУ операцию.
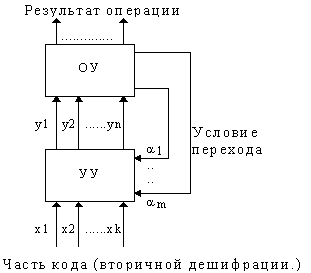
Рисунок. Структура АЛУ
Подробная структура АЛУ представлена на рисунке.
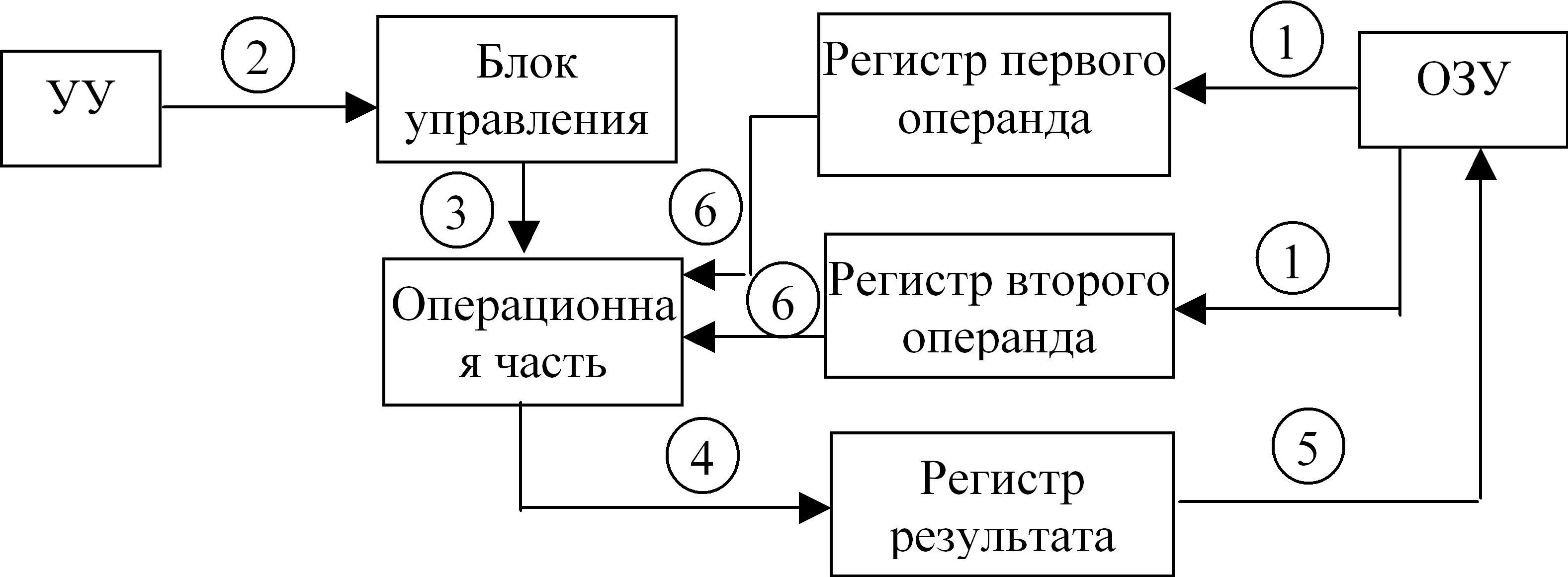
Исходные данные (операнды) по командам УУ считываются из ОЗУ в регистры первого и второго операндов (связь 1).
Из УУ в блок управления АЛУ поступает команда на выполнение той или иной операции (связь 2), которая передается им в операционную часть (связь 3).
В соответствии с этой командой операционная часть выполняет нужное действие с данными, которые выбираются из регистров первого и второго операндов (связь 6). Результат заносится в регистр результата (связь 4), откуда – в ОЗУ (связь 5).
Структура регистров АЛУ, куда помещаются исходные и результирующие данные, а также размер регистров (число двоичных разрядов) формируют понятие разрядной сетки.
Набор выполняемых в АЛУ операций должен обладать функциональной полнотой. Чтобы обеспечить функциональную полноту достаточно четырех операций:
- обращение к памяти для записи/чтения данных;
- инкремент/декремент;
- сравнение (реализует возможность условного перехода);
- останов работы устройства.
Базаров Н.Р. 1
1 : Колледж коммерции, технологий и сервиса ФГБОУ ВО «Курский государственный университет»
Работа в формате PDF
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Арифметико-логическое устройство (АЛУ) предназначено для выполнения арифметических и логических преобразований над числами и словами.
В АЛУ кроме классических арифметических операций, логического сложения и логического умножения двух слов выполняются сдвиги слов, преобразования кодов и некоторые другие операции.
Современные АЛУ выполняют:
- функции двоичной арифметики для данных в формате с фиксированной точкой;
- функции двоичной арифметики для данных в формате с плавающей точкой;
- функции арифметики двоично-десятичного представления данных;
- логические операций (в том числе сдвиги арифметические и логические);
- операции пересылки данных;
- работу с символьными данными;
- работу с графическими данными.
Основные характеристики АЛУ можно разделить на количественные и качественные.
Количественные характеристики определяют скорость выполнения операций, время выполнения одной операции, точность представления данных, количество выполняемых операций.
Среднюю скорость выполнения операций Vср. в АЛУ можно определить как отношение N(T)- количества операций, выполненных за отрезок времени Т к данному отрезку времени:
Среднее время, которое АЛУ тратит на выполнение операции равно: Tср = 1/Vср (2)
Точность представления данных в АЛУ зависит от разрядной сетки АЛУ и выбранного формата данных.
К качественным характеристикам АЛУ относятся:
- структурные особенности АЛУ;
- форматы представления данных (с фиксированной или плавающей точкой);
- способы кодирования данных.
АЛУ можно классифицировать по ряду признаков, приведенных ниже.
1. Классификация по способу представления данных:
- с фиксированной запятой;
- с плавающей запятой.
2. Классификация по способу действия над операндами:
·последовательные АЛУ, где каждая операция выполняется последовательно над каждым разрядом;
·параллельные АЛУ, операция выполняется над всеми разрядами данных одновременно;
·последовательно — параллельные АЛУ, где слово данных делится на слоги, обработка данных ведется параллельно над разрядами слога и последовательно над слогами.
3. Классификация по использованию систем счисления:
- двоичная;
- двоично- десятичная;
- восьмеричная;
- шестнадцатеричная;
- и т.д.
4. Классификация по характеру использования элементов и узлов:
- блочные — для выполнения отдельных арифметических операций в структуру АЛУ вводят специальные блоки, что позволяет процесс обработки информации вести параллельно;
- конвейерные — в конвейерных АЛУ операция разбивается на последовательность микроопераций, выполняемых за одинаковые промежутки времени (такты) на разных ступенях конвейера, что позволяет выполнять операцию над потоком операндов каждый такт;
- многофункциональные — это универсальные АЛУ, выполняющие множество операций в одном устройстве. В таких АЛУ требуется настройка на выполнение данной операции при помощи кода операции.
5.Классификация по временным характеристикам.
По временным характеристикам АЛУ делятся на:
- синхронные — в синхронных АЛУ каждая операция выполняется за один такт.
- Асинхронные — не тактируемые АЛУ, обеспечивающие высокое быстродействие, так как выполняются на комбинационных схемах.
6.Классификация по структуре устройства управления:
- АЛУ с жесткой логикой устройства управления;
- АЛУ с микропрограммным управлением.
Структура АЛУ представлена на рисунке 1.
Рисунок 1 – Структура АЛУ
Исходные данные (операнды) по командам УУ (см выше) считываются из ОЗУ в регистры первого и второго операндов (связь 1).
Из УУ в блок управления АЛУ поступает команда на выполнение той или иной операции (связь 2), которая передается им в операционную часть (связь 3).
В соответствии с этой командой операционная часть выполняет нужное действие с данными, которые выбираются из регистров первого и второго операндов (связь 6). Результат заносится в регистр результата (связь 4), откуда – в ОЗУ (связь 5).
Структура регистров АЛУ, куда помещаются исходные и результирующие данные, а также размер регистров (число двоичных разрядов t) формируют понятие разрядной сетки (далее – сетки), которое используется ниже.
Таким образом, структура АЛУ определяется набором микроопераций, необходимых для выполнения заданных арифметических, логических и специальных операций, а задачу построения АЛУ можно свести к задаче определения набора микроопераций, который позволяет составить микропрограмму любой из заданных операций. Такой набор легко получить, если записать микропрограммы всех операций, выполняемых в АЛУ, и выбрать из них все микрооперации, входящие в микропрограммы хотя бы один раз. Однако, если при этом алгоритм операций выбирать произвольно, то количество микроопераций, входящих в полный набор, может оказаться слишком большим и, следовательно, АЛУ будет сложным.
Для получения более простой схемы АЛУ алгоритмы арифметических и логических операций следует выбирать из условия получения минимального набора микроопераций. При этом необходимо учитывать требование обеспечения заданного быстродействия АЛУ: слишком ограниченный набор микроопераций может привести к «длинным микропрограммам некоторых операций», что увеличивает время выполнения данных операций.
Список использованных источников
- Арифметико-логическое устройство [Электронный ресурс] Режим доступа: http://www.studfiles.ru/preview/3565590/page:3/ Дата обращения: 07.02.2017
- Арифметико-логическое устройство [Электронный ресурс] Режим доступа: http://www.intuit.ru/studies/courses/60/60/lecture/1770%3Fpage%3D1 Дата обращения:07.02.2017
- Арифметико-логическое устройство. Общие сведения, функции и классификация [Электронный ресурс] Режим доступа: http://www.studfiles.ru/preview/716008/ Дата обращения: 07.02.2017
Арифметико-логическое устройство
Аннотация: Рассматриваются особенности реализации арифметико-логического устройства компьютера на примере проектирования АЛУ для умножения чисел с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя.
Классическая ЭВМ состоит из трех основных устройств: арифметико-логического устройства , устройства управления и запоминающего устройства. Рассмотрим особенности организации этих устройств. Прежде всего, рассмотрим структуру арифметико-логического устройства .
В современных ЭВМ арифметико-логическое устройство не является самостоятельным схемотехническим блоком. Оно входит в состав микропроцессора, на котором строится компьютер . Однако знание структуры и принципов работы АЛУ весьма важно для понимания работы компьютера в целом. Для лучшего понимания этих вопросов проведем синтез арифметического устройства, предназначенного для выполнения только одной операции – умножения чисел с фиксированной запятой , заданных в прямом коде, со старших разрядов множителя [13] . В ходе этого процесса также обратим внимание на особенности использования рассмотренных выше основных схемотехнических элементов ЭВМ.
Синтез АЛУ проходит в несколько этапов. Сначала необходимо выбрать метод, по которому предполагается выполнение операции , и составить алгоритм соответствующих действий. Исходя из алгоритма и формата исходных данных, следует определить набор составляющих АЛУ элементов. Затем требуется определить связи между элементами, установить порядок функционирования устройства и временную диаграмму управляющих сигналов, которые должны быть поданы на АЛУ от устройства управления.
Пусть операнды имеют вид:
[X]пк = x0x1x2…xn [Y]пк = y0y1y2…yn
где x0 , y0 – знаковые разряды.
Операция умножения чисел с фиксированной запятой , заданных в прямом коде, со старших разрядов множителя выполняется по следующей формуле:
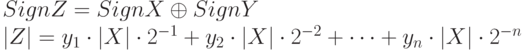
![[X]_</p><p>= 0.1101; Sign X = 0 \ [Y]_ = 1.1011; Sign Y = 1 \ Sign Z = 0 oplus 1 = 1 \ |X| = 0. 1 1 0 1 \ |Y| = 0. 1 0 1 1 \ y_y_y_y_ \ +0.00000000 |Z| = 0 \ y_ = 1 0.01101000 1 cdot |X| cdot 2^ \ + ovwerline |Z| = |Z| + |X| cdot 2^ \ y_ = 0 0.00000000 0 cdot |X| cdot 2^ \ + overline |Z| = |Z| + 0 \ y_ = 1 0.00011010 1 cdot |X| cdot 2^ \ + overline |Z| = |Z| + |X| cdot 2^ \ y_ = 1 0.00001101 1 cdot |X| cdot 2^ \ overline |Z| = |Z| + |X| cdot 2^](https://intuit.ru/sites/default/files/tex_cache/7af37921efed33c4bbe7f79df3e492e3.png)
Алгоритм вычислений представлен на рис. 3.1
Рис. 3.1. Алгоритм операции умножения чисел с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя
Каждой переменной, представленной в алгоритме, в схеме должен соответствовать элемент хранения. Разрядность модуля произведения равна сумме разрядностей сомножителей. Умножение двоичного числа на 2 -i обеспечивается сдвигом этого числа вправо на соответствующее количество разрядов. Переход к анализу очередного разряда множителя ( i = i + 1 ) может быть обеспечен сдвигом регистра множителя на один разряд в сторону старших разрядов.
Исходя из этого, определим состав оборудования, необходимого для реализации АЛУ заданного типа для n = 4 ( таблица 3.1).
| Регистр модуля множимого RGX | 8 | Загрузка. Сдвиг в сторону младших разрядов. | УС1 УС2 |
| Регистр модуля множителя RGY | 4 | Загрузка. Сдвиг в сторону старших разрядов. | УС3 УС4 |
| Регистр модуля результата RGZ | 8 | Загрузка. Установка в » 0 «. | УС5 УС6 |
| Триггер знака множимого TX | Загрузка | УС7 | |
| Триггер знака множителя TY | Загрузка | УС8 | |
| Триггер знака результата TZ | Загрузка | УС9 | |
| АЛУ | 8 | Комбинационный сумматор | – |
| Комбинационные схемы | Получение на входе АЛУ сигналов » 0 » или RGX в зависимости от значения yi | – |
Структурная схема устройства представлена на рис. 3.2.
Сравнитель
Теперь построим схему, которая получает на входе два байта, сравнивает их и определяет равны ли они между собой, либо первый байт больше второго. Помимо этого эта схема будет делать операцию XOR между этими байтами и отправлять результат на выход. Два одном, так сказать.
Как мы сравниваем двоичные числа? Сначала сравниваем первые цифры, если какая-то цифра больше, то и само это число больше.
Если же эти цифры равны, то сравниваем вторые числа, если какое-то из них больше, то и само число, содержащее эту цифру больше. Если они снова равны – то переходим к третьим по-счету цифрам и т.д. В итоге окажется, что либо какое-то число, либо числа равны. Построим логическую схему, которая выполняет подобный алгоритм. Рассмотрим элемент схемы, сравнивающий значения двух текущих битов.
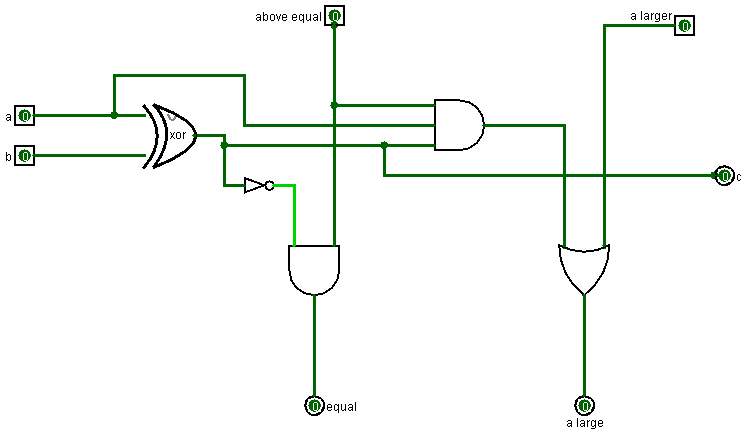
На выход a и b подаются текущие значение битов двух чисел, которые мы сравниваем.
Логика сравнения основано на принципе, описанном выше. Операция сравнения двух текущих битов некого числа зависит от результатов сравнения двух предыдущих битов. Если значение предыдущего бита числа a было больше чем значение предыдущего бита числа b, то на вход a lager подается единица, а на вход above equal – ноль. Это означает, что число a больше числа b, значит на выходе схема при любых текущих значениях битов чисел a и b выдает единицу на выход a lager. На выход c схема всегда выдает результат операции a XOR b, это ее дополнительная функция помимо сравнения.
Если предыдущее значение бита a меньше чем предыдущее значение бита b, то и само число a меньше числа b. Тогда схема имеет нули на входах above equal и a larger. И, соответственно, выдает нули на выходы equal и a larger.
Если предыдущие значения битов чисел a и b равны, то схема получает единицу на вход above equal, и ноль на вход a lager. В таком случае схема сравнивает текущие значения битов a и b. И, если они равны, выдает единицу на выход equal и ноль на выход a lager, если бит a больше бита, b выдает единицу на выход a lager и ноль на выход equal, а если биты a и b равны выдает нули на оба этих выхода.
Эта схема, сравнивающая отдельные биты (битовый сравнитель) в виде единого блока выглядит так:
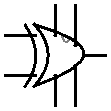
Теперь рассмотрим устройство сравнителя, который может сравнивать два байта друг с другом:
Как видно, схема содержит в себе восемь битовых сравнителей.
На входы мы подаем байты a и b. Мы сравниваем каждый бит соответствующих разрядов этих байтов. Если они равны, то на выходе equal единица, а на выходе lager 0. Если a больше b, то — наоборот. Если b больше a, то на обоих этих выходах нули. Помимо сравнения эта схема также ксорит (делает операцию XOR) два входящих байта и выдает получившийся третий байт.
Байтовый сравнитель в виде единого блока выглядит так:
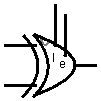
Арифметико-логическое устройство целиком
Теперь объединим все упомянутые выше схемы в рамках одного устройства:
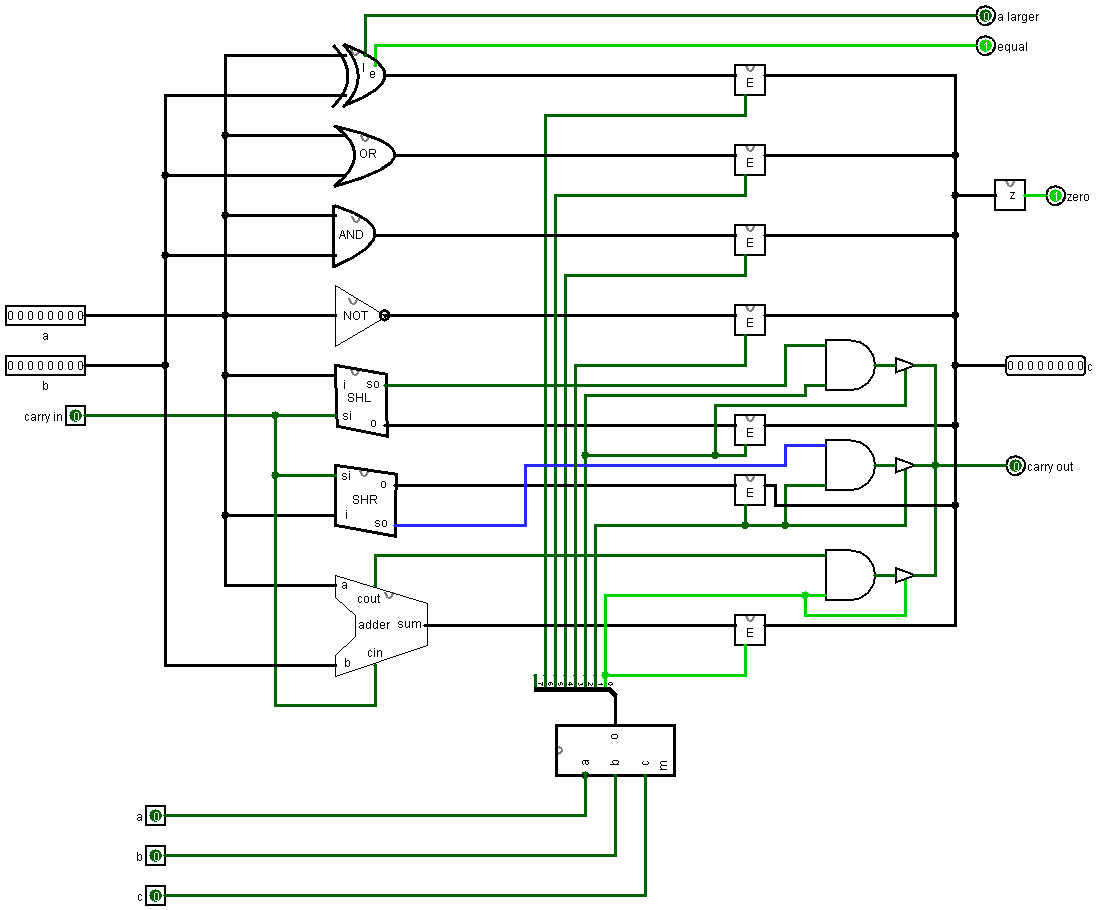
Блоки E это энейблеры, которые пропускают либо блокирует входящий сигнал. В зависимости от значений нижних входов (один – пропустить, ноль – блокировать).
Смысл такой, что мы имеет два байта, над которыми хотим сделать какие-либо операции. Значения этих байтов передается в блоки, которые мы описали выше (шифтер, adder и т.д.) Блоки выполняют необходимые операции, но информация с результатами всех этих операций останавливается на энейблерах. В самом низу мы видим декодер, с помощью которого мы можем выбрать, какой энейблер мы хотим активировать. То есть мы можем выбрать какая именно операция из возможных нас интересует и пропустить ее результаты на выход. Что бы лучше в это вкинуть, откройте в Logisim’е эту схему и посмотрите на нее на практике.
Арифметико-логические устройства (АЛУ)
Назначение АЛУ. Арифметико-логические устройства предназначены для выполнения арифметических и логических операций над «-разрядными операндами А = An х. АхА0иВ = Вп j. BxB0. Вид выполняемой операции задается сигналом M (Mode – режим). Например, 4-разрядные АЛУ (п = 4) выполняют 16 арифметических (М = 0) и 16 логических (M= 1) операций. Выбор одной из арифметических или логических операций осуществляется с помощью 4-разрядного кода E3E2EiE0. Логические операции над операндами выполняются поразрядно

где знак «*» – любая двуместная операция алгебры логики (ИЛИ, И, ИЛИ-HE, И-НЕ, исключающее ИЛИ и др.).
Помимо операндов на вход АЛУ подается сигнал переноса C0. Результат выполнения операции снимается с выходов в виде функций Fj (г = 0,1,2,3) для отдельных разрядов. При выполнении арифметических операций АЛУ представляет собой 4-разрядный сумматор с параллельным переносом. Поэтому в АЛУ, как и в сумматоре, имеются выходы переноса C4, G и Р, используемые для последовательного или параллельного каскадирования 4-разрядных секций. Рассмотрим функции и принципы построения 4-разрядных АЛУ.
Функции АЛУ
Основой для построения АЛУ служат двоичные сумматоры, для которых выражение (4.20) суммы г’-го разряда имеет вид

(4.20)
Для выполнения логических операций и расширения функциональных возможностей сумматора примем следующие меры:
Арифметико-логическое устройство
Арифметико-логическое устройство (АЛУ) предназначено для выполнения арифметических и логических операций преобразования информации. Функционально АЛУ (рис. 5.2) состоит обычно из двух регистров, сумматора и схем управления (местного устройства управления).
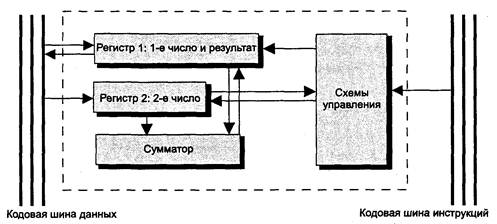
Рис. 5.2. Функциональная схема АЛУ
Сумматор — вычислительная схема, выполняющая процедуру сложения поступающих на ее вход двоичных кодов; сумматор имеет разрядность двойного машинного слова.
Регистры — быстродействующие ячейки памяти различной длины: регистр 1 имеет разрядность двойного слова, а регистр 2 — разрядность слова. При выполнении операций в регистр 1 помещается первое число, участвующее в операции, а по завершении операции — результат; в регистр 2 — второе число, участвующее в операции (по завершению операции информация в нем не изменяется). Регистр 1 может и принимать информацию с кодовых шин данных и выдавать информацию на них; регистр 2 только получает информацию с этих шин.
Схемы управления принимают по кодовым шинам инструкций управляющие сигналы от устройства управления и преобразуют их в сигналы для управления работой регистров и сумматора АЛУ.
АЛУ выполняет арифметические операции «+», «-», «х» и «> только над двоичной информацией с запятой, фиксированной после последнего разряда, то есть только над целыми двоичными числами. Выполнение операций над двоичными числами с плавающей запятой и над двоично-кодированными десятичными числами осуществляется с привлечением математического сопроцессора или по специально составленным программам.
Рассмотрим в качестве примера выполнение команды умножения. Перемножаются числа 1101 и 1011 (числа для простоты взяты 4-битовыми). Множимое находится в регистре 1, имеющем удвоенную по отношению к регистру 2 разрядность; множитель размещается в регистре 2. Операция умножения требует для своего
Физическая и функциональная структура микропроцессора
выполнения нескольких тактов. В каждом такте число из регистра 1 проходит в сумматор (имеющий также удвоенную разрядность) только в том случае, если в младшем разряде регистра 2 находится 1. В данном примере в первом такте число 1101 пройдет в сумматор, и в этом же первом такте число в регистре 1 сдвигается на 1 разряд влево, а число в регистре 2 — на 1 разряд вправо. В конце такта после сдвигов в регистре 1 будет находиться число 11010, а в регистре 2 — число 101. Во втором такте число из регистра 1 пройдет в сумматор, так как младший разряд в регистре 2 равен 1; в конце такта числа в регистрах опять будут сдвинуты влево и вправо, так, что в регистре 1 окажется число 110100, а в регистре 2 — число 10. В третьем такте число из регистра 1 не пройдет в сумматор, так как младший разряд в регистре 2 равен 0; в конце такта числа в регистрах будут сдвинуты влево и вправо, так что в регистре 1 окажется число 1101000, а в регистре 2 — число 1. На четвертом такте число из регистра 1 пройдет в сумматор, поскольку младший разряд в регистре 2 равен 1; в конце такта числа в регистрах будут сдвинуты влево и вправо, так что в регистре 1 окажется число 11010000, а в регистре 2 — число 0. Поскольку множитель в регистре 2 стал равным 0, операция умножения заканчивается. В результате в сумматор последовательно поступят и будут сложены числа: 1101, 11010, 1101000; их сумма 10001111 (143 в десятичной системе) и будет равна произведению чисел 1101 х 1011 (13 х 11 десятичные).
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:




